статора вращается против часовой стрелки и может рассматриваться как роторная обмотка. Уравнения ЭДС такого двигателя совпадают с уравнениями ЭДС обобщенной мащины, приведенными в § 1-2. Для установившегося синхронного режима в матрице Z (1-6) надо принять р = О, сор = со. Найдем вектор приложенного напряжения. В режиме холостого хода угол 9 (между осью полюсов ротора и осью магнитного потока статора, соответствующего приложенному напряжению) равен нулю; поток полюсов индуцирует в поперечном контуре ЭДС, которая уравновешивается приложенным напряжением (рис. 4-5, а). При работе двигателя под нагрузкой магнитное поле статора уходит вперед на угол 6 отно-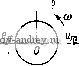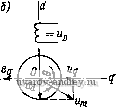

Рис. 4-5. Упрощенные векторные диаграммы напряжений синхронного двигателя: а - на холостом ходу; б - под нагрузкой

сительно полюсов (см. рис. 4-2). Вектор приложенного напряжения в системе координат, связанной с полюсами, отстает на угол 6 от положения, соответствующего режиму холостого хода, и занимает положение, указанное на рис. 4-5, б. Составляющие этого вектора по осям d а q равны

Ui=-Um sin е = -Y2U sin 6; = f/ cos е = V2 f/cos е,

где и - действующее значение фазного напряжения. Уравнения ЭДС синхронного двигателя примут вид

Напомним: r - активное сопротивление фазы статора.

Контур Q исключен, так как ток в нем в установившемся синхронном режиме равен нулю. Из этих уравнений следует: /д = = Uolfo, ток в обмотке возбуждения постоянен, что соответствует постоянной НС полюсов. Противо-ЭДС вращения в контуре q от продольного потока полюса Xmdid = Y2 Е тоже постоянна. 86

Это позволяет число уравнений ЭДС синхронного двигателя сократить до двух:

d Я

- i/sine (/cose-£

(4-1)

Этой системе уравнений соответствует известная векторная диаграмма токов и напряжений синхронного двигателя, изображенная на рис. 4-6, а. Обычно токи и напряжения синхронного двигателя рассматривают с противоположным знаком, а вместо амплитуд вводят действующие значения. В этом случае получим более удобную векторную диаграмму напряжений, расположенную в первом квадранте (рис. 4-6, б).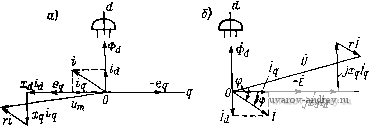

Рис. 4-6. Векторные диаграммы токов и напряжений синхронного

двигателя

ч

Выражение для момента получим из формулы (1-11)

M = {Ld-L)idig + MDioig или, с учетом приведенного выше выражения для е^,

M[{Xd-х^)idiq + V-?] (4-2)

Решая уравнения ЭДС относительно токов id и i находим . /2 ( ~ + <?cos6) -

л -f XdXg

. у-2 Q + sin 9) - гЕ

+ XdXq

(4-3)

Подставляя эти выражения для токов в формулу (4-2), можно получить Зависимость синхронного момента двигателя от его параметров, приложенного напряжения и степени возбуждения машины, определяемой величиной Е. При учете всех параметров эта зависимость получается достаточно сложной. В крупных машинах обычно принимают г 0; тогда

idY2{-E + Uzoslxd; igY2{V smQ)lx

и

\ Xq Xd J.

sin 26.

Первая составляющая момента^ обусловленная магнитным потоком возбуждения, называется основным синхронным моментом; вторая составляющая - от явнополюсности ротора - реактивным моментом. В трехфазных машинах за параметры Xd и Xq принимаются параметры одной фазы и выражение для момента надо умножить на г- Для определения влияния активного сопротивления статора на момент двигателя выполним вычисления, учитывая только первую степень г в выражениях токов и момента, т. е. пренебрежем членом по сравнению с л^, х^ и XdXq. Из выражений (4-3) получаем

£-fi/(cose

sine

Xd L V2 Г

- -£-f i/fsinG

Xd \

cosG

Подставляя id и в формулу (4-2) и выполняя несложные алгебраические преобразования, находим

2 ие+Г2-

Xd \

м = -

-] cos е

Xq }

X f iV 1 + f L L) [sin 26 + г f-L + L) cos 26]

\ Xq / J 2 \ Xq Xd j i \ Xd Xq j

к

Преобразуя тригонометрические функции по формулам приведения, будем иметь

М

Sin (в + 8i) -f f-l---L) Sin (26 -f 8,) -

z \ Xq Xd j

(t--)1.

(4-5)

где

Xd \ Xq J \ Xd Xq J

Jq / \ Jd

Из формулы (4-5) следует, что синхронный момент двигателя содержит три составляющие: основной синхронный момент

Mi=-sin(6 + ei); (а Xd

реактивный синхронный момент от явнополюсности ротора

,= J( L L)3in(26-fe,); (а \ Xq Xd J

И не зйвисящий от угла б момент сопротивления

2г Г

Из сравнения формул (4-4) и (4-5) следует, что влияние активного сопротивления статора на синхронный момент сводится к появлению постоянного момента Мо и смещению кривых момента на углы ие, пропорциональные активному сопротивлению статора. Для неявнополюсного двигателя с электромагнитным возбуждением Xd= Хд и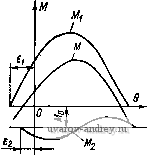

Рис. 4-7. Зависимость моментов синхронного двигателя от угла 9

Рис. 4-8. Зависимость асинхронных моментов синхронного двигателя от скольжения

7W =

rsin(6-fei)-8-

Xd L

Xd J

(4-6)

где e = EIU - степень возбуждения двигателя.

Максимальный момент двигателя будет при sin (6 -f е,)

М

макс -

ш Xd

Этот момент имеет наибольшее значение при степени возбуждения е = xJii.r)- Расчет момента двигателей с постоянными магнитами необходимо проводить по общей формуле (4-5), имея в виду, что для этих машин Xd<iXq и реактивный момент при рабочих углах 6 направлен в сторону, противоположную направлению основного синхронного момента (рис. 4-7). Степень возбуждения двигателей с постоянными магнитами должна быть меньше, чем в двигателях с электромагнитным возбуждением; ее значение выбирается из условия пуска двигателя и входа его в синхронизм.

Пусковой режим. Вход в синхронизм. Одним из основных требоввний, предъявляемых к синхронным двигателям, является требование надежного пуска и входа в синхронизм. Необходимо, чтобы вращающие моменты, действующие иа ротор в процессе его разгона и при входе в синхронизм, были не меньше номинального момента двигателя. Пуск малогабаритных синхронных

Дви1-а*елей с постоянными МаРНиТаМи ocyщec1rвЛяetcй tteHoupeAcfвейныМ включением в сеть. Во время разгона Jna ротор кроме вращающего асинхронного момента и момента сопротивления нагрузки М„ действует еще тормозной момент Mr, возникающий от взаимодействия магнитного поля ротора с наведенными им в обмотке статора токами, протекающими по цепи статор- источник питания. Эти токи имеют частоту fi{l-s), где s - скольжение, и отличаются от частоты сети. На рис. 4-8 представлены кривые моментов, действующих иа ротор двигателя в процессе его разгона. Асинхронный момент при симметричном напрнжеиин на обмотке статора определяется по формуле (3-5).

Для вывода формулы тормозного момента рассмотрим векторную диаграмму синхронного двигателя (рис. 4-9), который можно рассматривать как генератор в режиме короткого замыкания. На диаграмме xd - (1-s)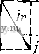

6=0,35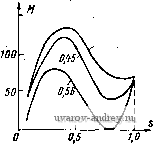

Рис. 4-9. Векторная диаграмма синхронного двигателя в режиме короткого замыкания

Рис. 4-10. Пусковые характеристики синхронного двигателя при различной степени возбуждения

я Xq = Xq (1 -s) - синхронные сопротивлении по продольной и поперечной осям двигателя при заданном скольжении. Из векторной диаграммы находим

Iq+xdId = E[;

-\q+rli = Q;

где Е' Е (1-s) - ЭДС фазы двигателя.

Тормозной момент равен потерям в активном сопротивлении фаз, деленным на угловую скорость:

2/2г

Шс(1 -S)

Подставляя сюда выражения для токов н сопротивлений xd и xq, полу-

2Е^ jl-sylr + d-sfx]

lr + {l-sfXdXqY

(4-7)

< Из этой формулы следует, что тормозной момент растет с увеличением степени возбуждения двигателя и активного сопротивления обмотки статора. По этим причинам в двигателях малых габаритов, имеющих большое актив-

ное сопротивление обмоток, степень возбуждения должна быть меньше, чем в двигателих больших габаритов. На рис. 4-10 приведены пусковые механические характеристики двигателя мощностью 2,5 Вт на частоту 50 Гц при различной степени возбуждения е.

Ротор синхронного двигателя с постоянными магнитами втягивается в синхронизм в конце пуска под действием сикхронизирующего момента. Вход в синхронизм происходит за весьма короткое время. Переход ротора от подсинхронной скорости к синхронной осуществляется скачком, поэтому входной момент сильно зависит от момента инерции ротора и связанного с ним нагрузочного устройства. Очевидно, что вход в синхронизм осуществляется тем лучше, чем выше подсиихрониая скорость ротора и больше синхронный момент.

Рассмотрим процесс входа в синхронизм с энергетической точки зрения. Двигатель войдет в синхронизм, если работа, совершаемая синхронным моментом, будет больше (или равна) суммы прироста кинетической энергии ротора и работы преодоления сопротивления нагрузки:

При синусоидальной зависимости Мс - Ломаке sin (9 -f Bi) получим

Дflк+4н.

синхронного

момента от

(4-8) угла 9

Ас= J M aKcsin(9-f ei)d9 = 2Af aKc-

Изменение кинетической энергии ротора

ДГ, = Уш2/2 - (1 - s )2/2 ycos ,

где I - момент инерции ротора.

Работу преодоления момента сопротивления нагрузки с учетом асинхронного момента двигателя при изменении s от Sgx До О найдем по формуле

\ Мн(1-s/sbx)<0c(1-s)di МнШсвх/2.

(4-9)

Продолжительность входа в синхронизм определяем из закона сохранения момента количества движения

УШС - (1 - Sbx) = .Мср^вХ-

Приняв Afcp =(2/я) Af aKc -jWh/2, получим

./tOcSBX

(2/я) М„акс - Л1н/2

Подставляя это значение в формулу (4-9), находим

<o?Sbx

Неравенство (4-8) примет вид

cWbx +

< вх

-Л- V

(4-10)

Соотношение (4-10) определяет при заданных Л1 акс и Мц скольжение асинхронного режима, при котором возможен вход двигателя в синхронизм.

Особенности рабочего режима. Рабочий режим синхронного двигателя с постоянными магнитами имеет ряд особенностей, которые обусловлены поведением постоянного магнита как источника НС возбуждения. Для определения рабочих свойств синхронного двигателя с постоянными магнитами прежде всего необходимо найти по кривой намагничивания положение прямой возврата, характеризующей магнитное состояние двигателя, и ЭДС в его обмотках.

Для двигателя с радиально расположенными магнитами (см. рис. 4-3) положение прямой возврата находим по пересечению кривой размагничивания постоянного магнита и вспомогательной прямой, называемой характеристикой противовключения Ф £ (рис. 4-11), Противовключение f возникает в асинхронном режиме

работы двигатеЛя при малых скольжениях, когда демпфирующее Ef действие токов короткозамкнутого

ротора ничтожно мало. В од-

Рис. 4-11. К определению точки отхода прямой возврата от кривой размагничивания в синхронном двигателе с радиально расположенными магнитами

Рис. 4-12. Схема замещения магнитной цепи двигателя по продольной оси

иом из положений ротора НС полюсов и НС обмотки статора оказываются направленными по одной оси навстречу друг другу.

В этом положении, называемом режимом противовключения, размагничивающее действие реакции якоря максимально. В ненасыщенных машинах можно использовать простую схему замещения магнитных сопротивлений, изображенную на рис. 4-12.

Здесь Fad - НС обмотки двигателя; F - НС постоянного магнита; м. Ro, Rs, Ru - магнитные сопротивления магнита, полей рассеяния магнита и обмотки, воздушного зазора.

Характеристика противовключения в относительных единицах имеет

вид

ф = £ = Ок/ - кцЕо,

(4-11)

где

R6 -f 1/Gs

- магнитная проводимость при коротком замыкании;

х(, Об 1

ku =

хб -\-Xs Об -f Gs

1 + R6Gs

--.коэффициент, учитывающий падение напряжения на индуктивности рассеяния.

ЭДС холостого хода двигателя

(4-12)

l+R6Gs

где Ер - ордината точки пересечения прямой возврата с характеристикой холостого хода, соответствующей магнитной проводимости llRt -f Go = Go-

У двигателя с аксиально расположенными магнитами наибольшее размагничивание магнита происходит в режиме короткого замыкания в момент подключения двигателя к сети при неподвижном роторе.

Для определения точки отхода прямой возврата от кривой размагничивания находим ток короткого замыкания /к по схеме замещения и умножаем его иа коэффициент 1,1-1,3, учитывающий переходную составляющую тока в момент включения.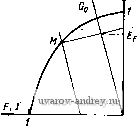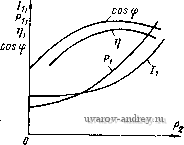

Рис. 4-13. К определению точки отхода прямой возврата в двигателе с аксиально расположенными магнитами

Рис. 4-14. Рабочие характеристики синхронного трехфазного двигателя с постоянными магнитами

Размагничивающая составляющая тока, приведенная к полюсам маг-

к. разм -

(1,1 1.3)/к

H-e(Ga4-G )

На диаграмме магнита (рис. 4-13), построенной в относительных единицах, по оси токов откладываем отрезок /к.разм и проводим прямую, параллельную прямой, соответствующей результирующей проводимости Gq, до пересечения с кривой размагничивания. Полученная точка и является искомой. ЭДС холостого хода находим по формуле (4-12).

Положительными свойствами синхронных двигателей с постоянными магнитами являются: высокая стабильность скорости в синхронном режиме, высокие энергетические показатели (КПД, cos ф). Недостаток - большая кратность пускового тока и более высокая стоимость по сравнению с аналогичными реактивными дви1-ателями. На рис. 4-14 приведен примерный вид рабочих характеристик синхронного трехфазного двигателя с постоянными магнитами.

4-3. Синхронный реактивный двигатель

Принцип работы. Устройство. Работа синхронного реактивного двигателя основана на взаимодействии кругового вращающегося магнитного поля статора с явнополюсным невозбужденным ротором. Для выяснения принципа работы положим, что поле статора

образовано двухполюсной обмоткой и неподвижно. Явнополюсный ротор (рис. 4-15, а) займет по отношению к полю статора положение, соответствующее максимальной магнитной проводимости. При повороте ротора вправо или влево от этого положения (рис. 4-15, б) возникает момент, который направлен в противоположную сторону и имеет максимальное значение, если угол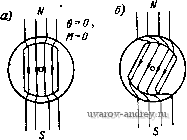

М=Ммакс

$ 90°, М=0

Рис. 4-15. Образование вращающего момента в реакгивном синхронном двигателе

поворота в = 45° (рис. 4-15, б). В положении, приведенном на рис. 4-15, в, 0 = 90°, момент также равен нулю, как и на рис. 4-15, а, но это положение ротора не является устойчивым. Полученная картина электромагнитных явлений будет такой же.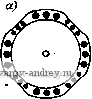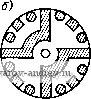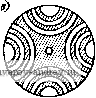

Рис. 4-16. Конструкции ротора синхронных реактивных двигателей

если поле статора и ротор вращаются синхронно с постоянной скоростью. Отсюда следует важный вывод, что постоянный синхронный момент возникает в двигателе только при синхронной скорости. Для запуска двигателя на его роторе устраивают коротко-замкнутую обмотку типа беличьей клетки. На рис. 4-16, а приведена типовая конструкция ротора реактивного двигателя; она получается путем фрезерования полюсов короткозамкнутого ротора асинхронного двигателя типа беличьей клетки. Лучшие результаты дают конструкции ротора, изображенные на рис. 4-16, б, в, соответственно для двухполюсной и четырехполюсной машины.

Векторная диаграмма и синхронный момент реактивного двигателя. Векторная диаграмма токов и напряжений синхронного ре-

активного Двигателя строится аналогично векторной диаграмме синхронного двигателя с постоянными магнитами (см. рис. 4-6, б) и изображена на рис. 4-17. Отличие состоит в том, что для реактивного двигателя £ = О и вектор тока всегда отстает по фазе от вектора напряжения. Уравнения ЭДС можно получить из уравнения (4-1), положив Я = О, или из векторной диаграммы:

r/.-V, = -sine;)

-fr/, = i/cose. I

Действующие значения токов находим по формулам (4-3) при Я = О или решая уравнения (4-13):

Ч и (Хд COS е - Г sin 6) -\/2 г^ + хахд

J iq и (Xi sin в -f- г cos в) i----

-Ь XiXq

(4-14)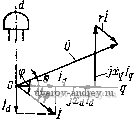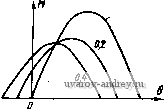

Рис. 4-17. Векторная диаграмма токов и напряжений реактивного двигателя

Рис. 4-18. Синхронный момент реактивного двигателя при различном отношении rlx

Угол 0 между вектором приложенного напряжения и поперечной осью двигателя q называется углом нагрузки. Его можно определить по экспериментальным данным U, /, cos ф и параметрам двигателя г, и д:,.. Действительно, из векторной диаграммы имеем

/, = /cos(ф-в); /d = /sin(ф-в).

Подставим эти значения во второе уравнение (4-13):

xal (sin ф cos в-cos ф sin G) -f /r(cos ф cos G -f sin ф sin G) = (/ cos G; отсюда

tgQ- и - Hxdmy + r cos Ф) / (r sin Ф - ACrf cos Ф)

Аналогично из первого уравнения (4-13) находим

tgG.

/ (Xq cos ф - г sin ф) (/ - / (ж, sin ф -f- г cos ф)

Момент двигателя определяем по формуле (4-2):

-f ГС08в) =

2U Xj-Xq

{x COS e-r sin 0) (Xrf sin 0 -b

\.{XdXq-r sin0COS0-f

(4-15)

-fr(*,COS e-XrfSin2 0)].

Выполняя над выражением в квадратных скобках несложные тригонометрические преобразования, получаем

где

t/ Xd-Xq

( +W [л/(Ч^)(гЧ4) sin(2e + ea)-r(*rf-A:,)]

(4-15а)

tge, = L(fl±i2L.

XdXq -

При Г < Xi, Г < Хд выражение (4-15 а) совпадает с приведенной выше формулой (4-5), если принять в ней Я = 0.

Максимальное значение момента будет при 20 + 88 = - 4

или

= Zi~x МгЧ/.) (гЧ4) -r(x.-.,)j.

Можно также найти значения угла 9, при которых момент равен нулю. Приравнивая нулю выражение в квадратнах скобках в формуле момента (4-15), находим

[х^Хд-г*) sin 0 cos 0 -f- rxg cos* 0-rxrf sin* e = 0, или, деля это уравнение на cos* 0, получаем

rxi tg* Q-(XiXg-r\gQ-rXg = Q. Решая это квадратное уравнение относительно tg в, находим

tgei = -r/xrf; tgea = V-На рис. 4-18 приведены кривые зависимости синхронного момента при различных значениях отношения rlx и при xjxg = 2. С увеличением активного сопротивления статора максимум синхронного момента достигается при углах, меньших 45°,м появляется постоянный тормозной момент, пропорциональный г (х^-д:,)*. Это приводит к более низкой перегрузочной способности синхронного реактивного двигателя по сравнению с аналогичной характеристикой синхронного двигателя с постоянными магнитами. .

Пуск двигателя. Вход в синхронизм. Пуск реактивных двигателей малой мощности осуществляетсн непосредственным включением в сеть переменного ТОКЕ. Поскольку ротор снабжея короткозамкнутой клеткой, то про-

цесс пуска происходит аналогично пуску асинхронного двигателя. Индуцируемые в короткозамкнутом роторе токи взаимодействуют с результирующим магнитным полем статора и образуют асинхронный вращающий момент Ма, который, преодолевая момент сопротивления нагрузки, разгоняет ротор.

При малых скольжениях под действием синхронного реактивного момента двигатель втягивается в синхронизм. Вследствие магнитной асимметрии ротора - неравенства параметров двигателя по продольной и поперечной осям - пуск реактявного двигателя, имеет некоторые особенности. Они обусловлены появлением в двигателе магнитного поля, вращающегося встречно основному полю, пульсациями вращающего момента и искажением кривой момента при скорости ротора, равной половине синхронной.

Точное выражение для асинхронного момента можно получить, исходя из уравнений ЭДС с исключенными контурами статора (демпферными контурами). Поскольку в асинхронном режиме скорость ротора t)= 1-s, а частота тока в контурах равна $ш, то в уравнениях обобщенной машины (1-23) надо заменить / иа /s и принять Еа= Ед= 0. Приложенные к контурам d W q напряжения равны и сдвинуты по фазе на 90°:

Ua=UiJ<*: Ug= jUel<*. Получим уравнение

где 0 = Ue> *.

Решая это уравнение относительно токов Id и Ig, находим

id= -lr-l{i-2s)Xg(ls)]; iq = - [г - / (1 - 2s) ха (Is)],

(4-16)

где

Д = г + jsr [Xd (jS) -Ь Хд (Is)] + (1 2s) Xrf (/S) Xg (Is).

Среднее значение асинхронного момента определяем в соответствии с формулой (1-25):

Мг= -Re[xa(is)ialg-xgOs)igla]. ш

Подставляя сюда выражения для токов, получаем

Ма = Re {Ixa Us)[г-Id- 2s) (Is)] [r + / (1 - 2s) д: (/s)] +

+ }Xq (ls)[r - i (I - 2s) Xa(ls)][r-\-1 (I-2s) xg (Is)]]. (4-17)

Расчет no этой точной формуле достаточно сложен, поэтому на практике используют приближенные методы. Для крупных машин принимают г = 0; тогда выражения для токов (4-16) упрощаются:

и

ixd(}s)

lq=-

jXq(}s)

4 Заказ № 678

Подставляя их в формулу для момента, находим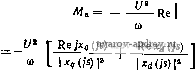

= 4~ [ Ф) + Re (is)

(4-18)

Значения Re/jf (/s) й Re/jf, (/s) легко найтн по схемам замещения дви-(рис 4. 9) °° ° поперечной осям для асинхронного режима работы

Но (2/0)) Re/дс (js) = М^ - момент асинхронного двигателя с равномерным зазором и параметрами, равными параметрам по поперечной оси.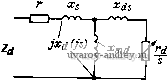

г xs

Рис. 4-19. Схемы замещения реактивного двигателя в асинхронном режиме

момент асинхронного двигателя с равномерным зазором и параметрами, равными параметрам синхронного двигателя по продольной оси. Поэтому к f в

Wa = (iWa , -Ь Marf). (4.19)

Для определения каждого из моментов машины может быть использована обычная схема замещения асинхронного двигателя. Момент асинхронного двигателя находится как среднее арифметическое его составляющих по осям d и 9. Это значение момента при / = О являетсн точным.

Ьсли же О, то в приближенных расчетах естественно использовать ту же формулу (4-19), определяя токи и по схемам замещения с учетом активного сопротивления статора (рис. 4-19). Такой метод расчета дает достаточно хорошие результаты при исключении области полусинхронной частоты, в которой наблюдаются провалы в кривой момента, обусловленные магнитной несимметрией ротора.

Рассмотрим выражение для момента при скорости, равной половине

синхронной, т. е. при S и / 0.

Выражения для токов U и упрощаются и принимают вид:

и

r + i---[xd(is) + xq(is)]

r + i-

= -iid.

[Xd(is) + Xq(js)]

(4-20)

Эти выражения показывают, что токи и при скорости, равной половине синхронной, зависят от среднего арифметического полных сопротивлений по продольной и поперечной осям, равны и сдвинуты по фазе на 90 .

Момент двигателя находится по такой же формуле, как н при г = 0. Подставляя выражения для токов (4-20) в формулу момента (1-25), получаем

Re \xi (ls)idild- хд (is) ( - jldld)} =

Re [jxd(is) + jxq(js)].

(4-21)

Формулы (4-i8) и (4-21) показывают, что точное значение момента при полусинхронной частоте можно получить, если соединить последовательно схемы замещения по осям dn q, подать на них напряжение 2U, а затем найти сумму потерь в цепях ротора по осям d п q. Точность расчета не зависит от активного сопротивления статора.

Таким образом, имеются достаточные основания считать, что средний асинхронный момент явнополюсной машины можно определить с удовлетворительной точностью для большого диапазона частот, соединив полные сопротивления по осям d w q параллельно, а при половинной синхронной скорости - последовательно.

На рис. 4-20 приведены кривые асинхронного момента в функции скольжения, рассчитанные по формуле (4-17). Приближенный метод не дает возможности обнаружить значительные провалы в кривой момента при скорости, близкой к полусинхронной, наблюдаемые у двигателей с большим активным

сопротивлением статора. Процесс втягивания реактивного двигателя в синхронизм происходит аналогично, как и в синхронных двигателях с постоянными магнитами. Полное решение вопроса входа реактивного двигателя в синхронизм требует решения уравнения движения ротора под действием среднего н пульсирующего электромагнитных моментов. Оно может быть выполнено с помощью аналоговой вычислительной машины (АВМ).

Рис. 4-20. Зависимость асинхронного момента реактивного % двигателя скольжения

4-4. Гистерезисные двигатели

Принцип работы. Устройство. Статор гистерезисного двигателя выполняется аналогично статору асинхронного двигателя: на нем имеется обмотка, создающая вращающееся магнитное поле (трехфазная, двухфазная с постоянно включенной емкостью, сосредоточенная с экранированным полюсом и т. п.). Ротор двигателя сделан из магнитно-твердого материала и обмотки не имеет. Вращающий момент гистерезисного двигателя возникает за счет сильно выраженного гистерезиса материала ротора. Сущность гистерезиса (используем гипотезу об элементарных магнитах) состоит в том, что при изменении (вращении) внещнего по отнощению к ротору магнитного поля элементарные магниты вследствие сил молекулярного трения устанавливаются (поворачиваются) по направлению поля с некоторым отставанием.

При включении обмотки статора в сеть переменного тока в машине образуется вращаюш,ееся магнитное поле; при этом наведенные полюсы ротора вращаются с той же частотой, что и полюсы статора. При отсутствии гистерезиса полюсы ротора располагаются точно под полюсами статора (рис. 4-21, а). Положим, что ротор набран из листов ферромагнитного материала, изолированных друг от друга так, что действием вихревых токов можно пренебречь. В этом случае между статором и ротором действуют только радиальные силы, уравновешивающие друг друга при равномерном зазоре. Вращающий момент, приложенный к ротору, равен нулю.

При наличии гистерезиса под действием сил молекулярного трения наведенные полюсы ротора смещаются относительно полюсов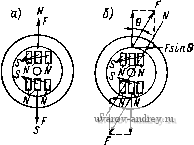

Рис. 4-21. К образованию вращающего момента в гистерезис-иом двигателе

Рис. 4-22. Механическая характеристика идеальной ги-стерезисиой машины

АД и СД - соответственно асинхронный и синхронный двигатель; АГ я СГ - асинхронный и синхронный генератор; Г - тормоз

статора на некоторый угол в (рис. 4-21,6). При взаимодействии полюсов статора и ротора появляется тангенциальная составляющая силы притяжения, которая обусловливает появление вращающего момента. Если момент нагрузки, приложенный к ротору, превышает гистерезисный момент при данном угле отставания 6, то этот угол, а вместе с ним и гистерезисный электромагнитный момент будут возрастать, пока не достигнут своего максимального значения, определяемого магнитными свойствами материала ротора, его объемом, распределением магнитной индукции.

Значение момента не зависит от скорости перемещения поля относительно ротора. Поскольку появление момента связано с наличием гистерезиса в ферромагнитном материале ротора, то его называют гистерезисным моментом, а двигатели, в которых этот момент является главным,- гистерезиснымн двигателями. Следует отметить, что гистерезисный момент существует и в обычных асинхронных двигателях с ротором беличья клетка . Однако для магнитно-мягких материалов магнитопровода ротора (листовая электротехническая сталь) гистерезисный момент столь незначителен, что его не учитывают.

При нагрузке, меньшей максимального гистерезисного момента, ротор двигателя приходит во вращение. В силу инерции ротора его скорость не может мгновенно сравняться со скоростью поля: имеет место асинхронный режим, при котором каждая точка ротора перемагничивается с частотой скольжения. За счет избыточного момента, равного разности гистерезисного момента и момента нагрузки, ротор двигателя достигает синхронной скорости, и гистерезисный двигатель работает как синхронный двигатель с постоянными магнитами. При этом ротор отстает от поля статора на угол 6, зависящий от момента нагрузки. При изменении нагрузки этот угол меняется; в случае внезапного изменения нагрузки наблюдаются качания ротора около нового положения равновесия. Механическая характеристика идеального гистерезисного двигателя (рис. 4-22) состоит из двух прямых: АВ - для асинхронного режима (М = const) и ВС - для синхронного режима (юр = = const). Если при синхронной скорости изменить знак момента, т. е. к машине подвести механическую мощность, то она перейдет в режим синхронного генератора (прямая CD). При превышении синхронной скорости в случае согласного вращения поля и ротора возникает режим асинхронного генератора (прямая DE). При различных направлениях вращения ротора и поля статора машина работает в режиме тормоза с постоянным моментом (прямая AF). Момент идеального гистерезисного двигателя

где Рэм = WrfiVp - электромагнитная мощность, передаваемая со статора на ротор при заторможенном двигателе. Здесь Шг - удельные потери на гистерезис за один цикл перемагничивания; fi - частота сети; Ур - объем активного материала ротора. Отсюда

WrVp

(4-22)

Из этой формулы следует, что момент гистерезисного двигателя тем больше, чем больше произведение WrVp. При ограниченной мощности возбуждения статора существует такой объем активного материала ротора, при котором WrVp максимально. Действительно, если Vp велико, то материал ротора полностью не намагничен {В„ и Н„ малы) н изменение намагниченности происходит по внутренней петле гистерезиса; это соответствует малому значению,Шр. Если Vp мало, то ротор быстро намагничивается и НС статора не может создать цикла перемагничивания с большими потерями. Отсюда следует, что можно подобрать такой объем активного материала ротора, при котором для заданной НС статора можно получить цикл перемагничивания по предельной петле гистерезиса.

Опыт проектирования гистерезисных двигателей показывает, что этому требованию удовлетворяют две конструкции ротора: ротор с немагнитной втулкой для относительно мягких гистере-

зисных материалов и ротор с магнитной втулкой для магнитно-твердых гистерезисных материалов. В обеих конструкциях активный слой ротора выполняется в виде тонкостенного цилиндра (рис. 4-23).

В первой конструкции ротора (рис. 4-23, а) магнитный поток проходит по гистерезисному слою тангенциально; между максимальной индукцией магнитного поля в воздушном зазоре и в гистерезисном слое ротора В^ существует соотношение

(4-23)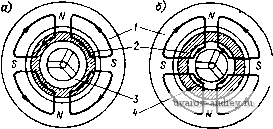

Рис. 4-23. Конструкции ротора гистерезисного двигатели: а - с немагнитной втулкой; б - с магнитной втулкой

/ - Магиитопровод статора; 2 - гистерезисиый слой; 3 - иемагиитиая втулка; 4 -магнитная втулка

Действительно, магнитный поток, приходящийся на пару полюсов,

я я 2р Р

С другой стороны, Ф = 2Б„Д/ (здесь А - толщина гистерезисного материала; D - диаметр ротора; / - активная длина машины).

Приравнивая потоки, получаем формулу (4-23). Поскольку D>2Ap, то Вт>Вв; магнитный поток проходит значительный путь по гистерезисному слою, поэтому коэрцитивная сила материала должна быть невелика. Для этой конструкции применяются магнитные материалы с относительно узкой петлей гистерезиса (Бт>0,8 Тл; Я„< 14.10- А/м).

Во второй конструкции ротора магнитный поток в гистерезисном слое проходит в радиальном направлении; при этом

Bm=Bi,. (4-24)

Длина линий индукции в гистерезисном слое равна А, поэтому для таких двигателей целесообразно применять магнитные материалы с широкой петлей гистерезиса (Я„>3-10* А/и).

Характеристики гистерезисных материалов. В синхронных двигателях с постоянными магнитами (см. § 4-2) рабочая точка магнита лежит на участке

петли гистерезиса, находящейся во втором квадранте. Этот участок харак-теризуется двумя величинами: остаточной индукцией Вг и коэрцитивной силой Не-

Энергия, развиваемая магнитом во внешнем пространстве, пропорциональна ВН. Эта энергия тем выше, чем больше петля гистерезиса приближается к прямоугольнику. Мерой приближения к прямоугольнику служит коэффициент выпуклости

(ВЯ)макс

№

Материал ротора гистерезисного двигателя намагничивается обмоткой статора в процессе пуска, при этом рабочая петля материала находится внутри предельной петли гистерезиса. Рабочая точка, определяющая максимальную индукцию в роторе в асинхронном режиме, находится не на спинке петли, а в ее вершине. Распределение индукции в роторезависит от формы рабочей петли гистерезиса. Для приближенного анадиза^пусковых свойств гистерезисного двигателярабочую петлю гистерезиса можно заменить равным по площади эллипсом (рис. 4-24). Уравнения эллипса в параметрической форме имеют вид

Н = Н^г cos at = Re Wmie ;

В = Bmi cos (ш - V) = Re Bmiei

(4-25)

Физические свойства гистерезисного материала можно характеризовать относительной комплексной магнитной проницаемостью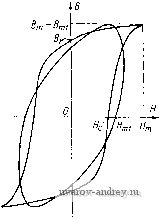

1*т =

Впл

= 1Ате =11 -i>2.

(4-26)

Рис. 4-24. Замена петли гистерезиса эквивалентным эллипсом

где Urn - модуль относительной магнитной проницаемости; [х^ и [Xj - консервативная и вязкая составляющие комплексной магнитной проницаемости.

Следует заметить, что для реальной петли гистерезиса при синусоидальном изменении индукции напряженность поля имеет несинусоидальную зависимость от времени, и в выражении (4-25) надо иметь в виду первую гармонику напряженности. Потери иа гистерезис за один цикл намагничивании

шг = НйВ = nHmiBmi sin у. (4-27)

Гистерезисиый угол у характеризует намагничивающую силу, необходимую для создания магнитного поля в гистерезисном слое ротора, которая в общем случае содержят две составляющие: реактивную f Дг, совпадающую по фазе с индукцией, и активную f дд, опережающую индукцию на 90° (рис. 4-25). Активная составляющая, пропорциональная sin -у, определяет потери на гистерезис, а реактивная составляющая, пропорциональная cos у,- реактявную мощность двигателя.

Величина sin у зависит от формы петли гистерезиса; в частности, если оси эллипса совпадают с осями координат, то 7 = 90° и sin 7 = 1. При прямоугольной петле гистерезиса sin у также равен 1, так как при синусоидальном изменения индукции первая гармоника напряженности магнитного поля опережает индукцию на 90 . Отсюда следует, что требование наилучшего приближения петли к прямоугольнику практически эквивалентно требованию максимального значения sin у.

Иногда для характеристики приближения формы петли к прямоугольной вводят коэффициент выпуклости петли как отношение площади петли к площади описанного прямоугольника со сторонами 2Вт и 2Нт

/Св = SAiBmHm). где Sp - площадь петли гистерезиса.

ф

Рис. 4-25. Векторная диаграмма НС гистерезисного двигателя

Рис. 4-26. Векторная диаграмма токов и напряжений гистерезисного двигателя

Нетрудно установить связь между /Св и sin у, Подставляя в формулу (4-27) 5г = Щ= nBmiHmisin V и полагая Вт = Bmi. получаем

-f 4sinY. 4 Пт

В настоящее время в качестве активного материала ротора гистерезисных двигателей обычно применяется викаллой, характеристики которого

наилучшим образом отвечают требованиям как асинхронного, так и синхронного режимов.

Векторная диаграмма и схема замещения двигателя в асинхронном режиме. Векторная диаграмма токов и напряжений двигателя в асинхронном режиме приведена на рис. 4-26. Здесь /в - составляющая тока статора, образующая НС воздушного зазора; /д- составляющая тока статора, образующая НС активного слоя ротора. Последняя состоит из двух частей: активной /до = /д sin у и реактивной /д,- = /д cos у; /ф == /j - ток статора двигателя (ток фазы. Этой диаграмме соответствует схема замещения, изображенная на рис. 4-27. По приведенной схеме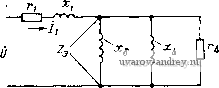

Рис. 4-27. Схема замещения гистерезисного двигателя в асинхронном режиме

/ф

7 . (4-28)

2э £ф

Из общего курса электрических машин известно: вектор НС т-фазной обмотки Fm = \/2т/фШэф/(яр); противо-ЭДСфазы - £ф = / (2я/-2) /Фшэф. Подставляя в формулу (4-28) значения - £ф и /ф, получаем

1 pFm 1,1,1

Выведем выражения для параметров схемы замещения д:б, и гд применительно к указанным выше двум типам конструкций ротора гистерезис-

Ршо^Тштгнитной втулкой. Амплитуда НС Fm состоит из двух частей- НС воздушного зазора и НС гистерезисного слоя:

[Хо п z ]Хо 2р [Xm(io

Заменяя Be в соответствии с формулой (4-23), получаем

V 2р^т )

i Вт С 2 V D

Подставляя значения Ф и /ш в формулу (4-29). будем иметь: 1 р'Ь , Dcosy

, Dsiny

Сравнивая это выражение с (4-29), находим

Хб = 2mf[Xo -- ш|

Г(4-30)

xд = 2rr.f,xo-i .?ф; DcosY

D sin Y

Из полученных формул следует, что гистерезисный слой ротора двигателя с немагнитной втулкой эквивалентен увеличению воздушного зазора на некоторую величину

4р2Дц

Ротор с магнитной втулкой. В этом случае Be бщ. = Вт Dllp,

Выполняя аналогичные преобразования, получаем

Dl 2

- эф;

хб = 2mf [Хо

р^б

XA:=2mfv,k: p Acosy *

lmDl

(4-31)

В этом случае имеем очевидный результат: гистерезисный слой ротора с магнитной втулкой соответствует увеличению воздушного зазора на величину (М\1т) е'-