которую можно получить формальным образом из уравнений (2-15) путем исключения токов ротора.

Решая уравнения (2-16) относительно токов If и /ьс, получаем

j UD(ZDb + Z)-iUoZDb

2ZDfZDb + Z(ZDf+ZDb) UD(ZDf + Z) + jUoZD! 2ZDfZDb + Z(ZDf + ZDb)

Ho ZDf + Z = ZQ +

- сопротивление прямой по-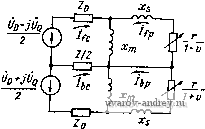

Uq-JUq 2

и a Фа z

7ш

Рис. 2-8. Схема замещения двухфазной неявнополюсной машины

следовательности фазы Q; Zob + Z = Zq-\-

Рис. 2-9. Упрощенная схема замещения двухфазной асинхронной машины

1 + г;

- со-

противление обратной последовательности фазы Q, а

2ZDfZDb + Z {ZDS + Zi>b) = Zd! (ZDb + Z) + ZDb {Zd! + Z) = = ZDfZQb + ZobZqf,

поэтому

ffc - ZQb - iUQZpb .

ZDfZpb + ZDbZqf

: OpZQf + jUQZDf

be--

ZofZQb + ZpbZQf

что совпадает с полученными выше выражениями для токов (2-12), Момент двигателя находим по формуле

(2-17)

(О

где Е'- вектор, составляющие которого равны коэффициентам при v в вн-Ражении Z/. Получим

М

= А R е [ /fp ( - jxjfc - jxifp) + I bp {]xm / be + ixf bp)} (0

= Jf Re i-ilfpifc + ftp/be)

(2-18)

Из (2-15) имеем

Ifp= --

ix +

Подставляя в формулу (2-18), находим

1 -г;

Рис. 2-10. Схема замещения однофазного асинхронного двигателя

= - и% Re Ы - о) - 1с Re Ы - d)1

(2-19)

Если в сеть включена только одна обмотка D. а вторая обмотка Q разомкнута (Zq = °о), то асинхронная машина работает в режиме однофазного двигателя. Соответствующая этому режиму работы схема замещения получится из рис. 2-8 при (/q = О и Z = 00. Она изображена на рис. 2-10.

В том случае, когда фазы D и Q не перпендикулярны, а смещены на некоторый угол а (см. рис. 2-1), формулы для НС прямой и обратной последовательности имеют вид

2

(2-20)

L (f/ f>-/ );

sin a

sin a

(2-21)

вид

Соответственно этому матрица преобразования для токов статора имеет

sin а j

L sin а

sin a

-/ sin a

Матрица сопротивлений такой машины получается по общему правилу и в осях, связанных с обмотками статора, имеет вид

Для перехода к уравнениям ЭДС симметричных составляющих используем матрицу преобразования для токов

Новая матрица сопротивлений и вектор напряжений находятся по формулам

т

: С ZC;

и =си.

Соответствующие вычисления предлагается читателю выполнить самостоятельно. В результате получаем

/р

+ fXm -

-/2a

2sinia > 2sinia

Z -fZ,2a z + Z

2sin2a ixm(l-v) 0

2 sin* a

fp jXm

jXm(l+V)

r+jx(l-v) 0

fXm 0

r + ix(l + v)

ЧАСТЬ ВТОРАЯ

ЭЛЕКТРОДВИГАТЕЛИ МАЛОЙ МОЩНОСТИ ОБЩЕГО ПРИМЕНЕНИЯ

Глава, третья АСИНХРОННЫЕ ДВИГАТЕЛИ

3-1. Основные типы асинхронных двигателей

Асинхронные двигатели малой мощности общего применения используются для электропривода постоянной скорости вращения, в котором требования по поддержанию скорости сравнительно невелики. В зависимости от вида питающего напряжения и обмотки статора различают трехфазные, двухфазные и однофазные асинхронные двигатели.

Трехфазные асинхронные двигатели имеют на статоре трехфазную распределенную обмотку, ротор двигателя короткозамкнутый (обычно беличья клетка ). Теория работы этих двигателей при симметричном трехфазном питании изложена в общих курсах электрических машин и в настоящей книге рассмотрена весьма кратко (см. § 3-3). Двухфазные асинхронные двигатели малой мощности с короткозамкнутым ротором обычно используются как конденсаторные двигатели, в которых в одну из фаз включена емкость, обеспечивающая фазовый сдвиг токов в обмотках, близкий к 90°. Такие двигатели питаются от однофазной сети. Для получения малых скоростей рртора иногда применяют асинхронные индукторные двигатели, имеющие трехфазную или двухфазную обмотку на статоре и вторичную однофазную или многофазную обмотку, располагаемую также на стато^еУЧисло пар полюсов этих обмоток выбирается таким образом, чтобы исключить трансформаторную связь между обмотками. Ротор зубчатый, обмоток не имеет и выполняет роль модулятора магнитного поля. Во вторичную обмотку асинхронного индукторного двигателя включается активное сопротивление или емкость. Большинство асинхронных электродвигателей малой мощнти выполняется однофазными; они имеют однофазную рабочую обмотку на статоре и короткозамкнутый ротор. При наличии только одной обмотки на статоре и симметричном магнитопроводе однофазный асинхронный двигатель имеет пусковой момент, равный нулю, поэтому для получения пускового момента, отличного от нуля, в двигателе предусмотрена вторая, вспомогательная обмотка на статоре, ось которой сдвинута относительно оси основной обмотки на 90°.

Асинхронные Двигатели малой мощности можно разделить на следующие группы:

1) однофазные двигатели с реостатным пуском - включением активного сопротивления во вспомогательную обмотку (фазу) на время пуска;

2) однофазные двигатели с дросселем, включаемым во вспомогательную фазу на время пуска (на практике этот тип машин встречается весьма редко);

О

О

и

а

О

О

а

о

О

о

Рис. 3-1. Схемы включения однофазных асинхронных двигателей в сеть: а - с пусковым сопротивлением; б- с пусковым дросселем; в - с пусковым конденсатором; г - с рабочим конденсатором; д - с пусковым и рабочим конденсаторами; е - с экранированным полюсом

3) однофазные двигатели с включением конденсатора во вспомогательную фазу на время пуска;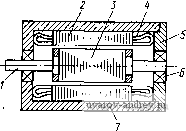

Рис. 3-2. Конструктивная схема асинхронного двигателя

; - вал; 2 - пакет статора; 3 - корот-козамкнутый ротор; 4 - обмотка статора; 5 - подшипниковый щит: 6 - подшипник; 7 - корпус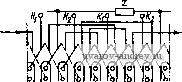

Г \( \< \( V \А

Рис. 3-3. Принципиальная схема асинхронного двигателя с двухзуб-цовыми обмотками

4) двухфазные конденсаторные двигатели с постоянно включенным рабочим конденсатором; иногда эти двигатели имеют дополнительный пусковой конденсатор, включаемый параллельно рабочему на время пуска;

5) универсальные асинхронные двигатели, рассчитанные для работы как от трехфазной, TajtJH однофазной сети переменного тока;

6) однофазные асинхронные двигатели с экранированными полюсами;

7) асинхронные индукторные двигатели.

На рис. 3-1 даны схемы включения однофазных асинхронных двигателей в сетьо своей конструкции однофазные асинхронные двигатели (исклк е1Гие составляют двигатели с экранированными полюсами) выполняются как неявнополюсные электрические машины с распределенными обмотками на статоре; ротор - коротко-замкнутый типа беличья клетка , как правило, со скосом пазов на одно зубцовое деление (рис. 3-2).

У двигателей первых трех типов, имеющих вспомогательную пусковую обмотку, главная фаза занимает */з всех пазов статора, а вспомогательная обмотка - V3 пазов. Иногда вспомогательная пусковая обмотка частично выполняется бифилярной; такой двигатель не требует внешнего пускового активного сопротивления, его функции выполняет бифилярная часть обмотки. Конденсаторные двигатели имеют на статоре две однотипные обмотки, сдвинутые в пространстве относительно друг друга на 90°. Универсальные асинхронные двигатели имеют симметричную трехфазную обмотку. Асинхронные двигатели с экранированными полюсами выполняются как явнополюсные машины с числом полюсов от двух до восьми. Полюсы имеют пазы, и часть полюса охвачена короткозамкнутым витком, служащим для образования вращающегося поля (см. § 3-8). Асинхронные индукторные двигатели имеют большое число различных модификаций как по форме магнитопровода, так и по схемам обмоток [13]. На рис. 3-3 в качестве примера приведена схема двухфазного асинхронного индукторного двигателя с двух-зубцовыми обмотками.

3-2. Величины, характеризующие работу асинхронного двигателя

, Асинхронные двигатели общего применения работают при номинальных напряжении и частоте сети, их частота вращения при изменении нагрузки колеблется незначительно: от частоты холостого хода По Л5 Пс = 60 fjp до номинальной частоты nj = = (1-Sf) Пс, где Sfj - номинальное скольжение. Зависимость момента, развиваемого двигателем, от частоты вращения имее вид, представленный на рис. 3-4. Здесь М„ - пусковой момент при п = 0; Mfj,- номинальный момент; Л1 акс - максимальный момент; Пк - критическая частота, соответствующая максимальному моменту.

Основным режимом работы асинхронных двигателей является номинальный режим; он характеризуется следующими данными: номинальной мощностью на валу Ралг! номинальной частотой вращения tif], об/мин; синхронной частотой поля с, об/мин; номи-

ййльным током /jv; КПД в номинальном режиме Т1д^; коэффициентом

мощности cos фд,.

По приведенным данным можно рассчитать и другие величины: номинальный момент

и - - I

потребляемую мощность

номинальное скольжение

= 1 - П^Пс.

Рис. 3-4. Механическая характеристика трехфазного асинхронного двигателя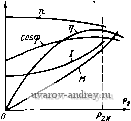

Рис. 3-5. Рабочие характеристики асинхронного двигателя

Для приближенной оценки пусковых свойств асинхронного двигателя приводят: кратность пускового тока 1 /1и; кратность пускового момента MJMif-, кратность максимального момента, или перегрузочную способность Двигателя М^кс/М^; максимальную добротность при пуске Мп пмакс; момент инерции ротора J;

Свойства двигателя при изменении момента на валу определяются его рабочими характеристиками, которые представляют собой зависимости потребляемого тока /, момента М, частоты вращения п, КПД т) и коэффициента мощности cos ф от полезной мощности на валу при. U = Uf а fi = fitj- На рис. 3-5 представлены типовые рабочие характеристики трехфазного асинхронного двигателя малой мощности.

3-3. Асинхронный двигатель в симметричном режиме

Многофазный асинхронный двигатель работает в симметричном режиме, если его обмотки одинаковы, а приложенные напряжения равны по амплитуде и смещены по фазе на угол 2я/т, где/п число фаз.

В трехфазной машине фазовый сдвиг между напряжениями равен 120°, а в двухфазной 90°. Двухфазную машину можно условно рассматривать как машину с четырьмя симметричными обмотками (рнс. 3-6), токи в которых смещены по фазе на 90°:

/i = /d; /2 = /q = d =

Отличительная особенность Симметричной асинхронной машййы tottont в том, что в ней образуется круговое вращающееся магнитное поле и электромагнитные процессы в фазах протекают одинаково, со смещением во времени на угол 2л/т.

Рассмотрим уравнения ЭДС и момента симметричного двухфазного двигателя (рис. 3-7). Напряжение, приложенное к фазе Q, при выбранном направлении вращения ротора опережает напряжение фазы D на 90 , т. е. On = jUd- Полагая Zd = Zq, уравнения ЭДС (2-15), выраженные через симметричные составляющие, запишем в виде (для удобства переставлены местами строки и столбцы и fp)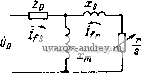

Рис. 3-6. Представление двухфазной машины в виде четырехфазиой Рис. 3-7. Электрическая схема двухфазного асинхронного двигателя Рис. 3-8. Схема замещения асинхронного двигателя в симметричном режиме

Zd + jXm jXm 0 0

6c 0

+ix

(3-1)

Как видно из этих уравнений, токи прямой и обратной последовательности в симметричной машине не зависят друг от друга. Поскольку при симметричной системе напряжений напряжение обратной последовательности равно нулю, то и токи, ему соответствующие, также равны нулю: /ьс =

= hp = 0.

Уравнения ЭДС двигателя примут вид

Zd+ jXm jXm

где s = 1-t; - скольжение.

Этой системе уравнений соответствует общеизвестная схема замещения асинхронного двигателя, изображенная на рис. 3-8. Токи в фазах статора и ротора равны

/fC =

; Ud .

(3-3)

здесь

L s J V s

или, если ввести обозначение а = 1 + Ео/Цхт),

А = /ДСт

o + Zd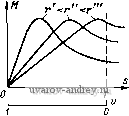

Рис. 3-9. Механические характеристики асинхронного двигателя при различном активном сопротивлении ротора

Рис. 3-10. Кривые моментов однофазного асинхронного двигателя

ДИМ

Подставляя эти выражения для токов в формулу момента (2-18), нахо-

М = 2

Полагая приближенно а = 1 +

(r/s + jXs)a + ZD Г Го + ixD

(3-4)

яй 1 --= 0, получим

IXm Хт

известную из общего курса электрических машин формулу момента симметричного двухфазного асинхронного двигателя

ris

с ( D + Orlsf + (JCDs + OXsf

(3-5)

Скольжение, при котором момент имеет наибольшее значение, называется критическим и находится из условия dMids = 0:

(3-6)

Соответствующий ему максимальный момент

Ломаке = -

rD-lrl + {xDs + X,f

(3-7)

Важная особенность этого выражения состоит в том, что максимальный момент симметричного асинхронного двигателя не зависит от активного сопротивления ротора; с изменением активного сопротивления ротора смещается максимум в кривой момента (рнс. 3-9).

Зависимости момента двигателя от скольжения можно придать более простую форму, если выразить момент в долях Ммакс- Используя приведенные выше выражения, нетрудно получить

М 1 + fltSK

= 2-

s/Sk + Sk/s -f 2aSK

(3-8)

где a= ro l(pr).

Выражение для момента (3-8) называется формулой Клосса.

3-4. Момент однофазного асинхронного двигателя

При включении в сеть одной обмотки асинхронного двигателя момент на валу образуется только при вращении ротора и направлен он в сторону вращения ротора. Качественно зависимость момента от угл,овой скорости наиболее просто проследить, исходя из теории вращающихси полей. Разложим пульсирующее магнитное поле однофазного двигателя на два вращающихся в противоположные стороны круговых поля. Кривые моментов, создаваемых каждым из этих полей, рассматривались в предыдущем параграфе; они имеют вид, представленный на рис. 3-10. Результирующий момент двигателя равен разности моментов от прямого и обратного вращающихся полей

Как видно из кривой, результирующий момент равен нулю при неподвижном роторе {v = 0); это обусловливает необходимость включения вспомогательной обмотки с фазосдвигающим сопротивлением при пуске двигателя (см. рис. 3-1). Для получения Зависимости момента однофазного асинхронного двигателя От его параметров и угловой скорости используем уравнения обобщенной электрической машины (1-23). Для данного случая неявнополюсной машины с одной обмоткой на статоре они имеют вид

r+}xU)

VX{j)

r + jx }

(3-9)

где r -\- jx - полное сопротивление обмотки ротора при разомкнутой обмотке статора; г -f jx Q) - полное сопротивление обмотки ротора при замкнутой накоротко обмотке статора; Ё = - jx----ЭДС ,

rD + j(Xm + Xds)

индуцируемая в обмотке ротора в режиме холостого хода. Момент двигателя в соответствии с формулой (1-25) будет

Л1 = Re [ - Idigx + Igiax (j) + j/gEl

,COc

(3-10)

Из уравнений (3-9) находим выражения для токов Ё , . . , Ё

.lr + jx(\-v)];

irv;

A==r + ir(x + x (/)] - XX (/) (l-v). Подставляя выражения для токов в формулу (3-10), получаем

£2

(Ос lai

rvlx(l-v) - r].

(3-11)

Отсюда видно, что при v = О момент двигателя равен нулю. В отличие от идеального трехфазного двигателя относительная скорость холостого хода

однофазного асинхронного двигателя всегда меньше синхронной и равна Уо =

--, а максимальный момент дви-

r >r >r

Рис. 3-11. Механические характеристики однофазного асинхронного двигателя при различном активном сопротивлении ротора

гателя зависит от активного, сопротивления ротора. На рис. 3-11 приведены кривые зависимости момента однофазного двигателя от скорости при различном активном сопротивлении ротора.

Аналогичную формулу момента можно найти из схемы замещения однофазного двигателя, полученной по методу симметричных составллющих и изображенной иа рис. 2-10. В этом случае с = /ьс = и

согласно формуле (2-19)

1 -V

+ / (.Хт + Us)

Выполняя несложные алгебраические квадратных скобках, находим

преобразования выражения в

М = -

-2xrv{x+x)

получим

2е)с -f 2г/ (Xm + Xs)- (Хт + Xs) (1 - г;)

Освобождаясь от мнимости в знаменателе и обозначая Хт + JCs = х,

ХтХГО

Формулы (3-11) и (3-12) отличаются тем, что в первой момент выражен через ЭДС в режиме холостого хода, а во второй - через ток, потребляемый главной фазой двигателя. Из обеих формул следует, что при г> X однофазная асинхронная машина при малых скоростях работает в тормозном режиме. Расчеты и опыт показывают, что максимальный момент однофазного асинхронного двигателя на 30-40% меньше, чем у трехфазного двигателя, выполненного в тех же габаритах.

3-5. Однофазный двигатель с пусковым сопротивлением

Как указывалось в § 3-1, для получения пускового момента, отличного от нуля, и улучшения пусковых свойств однофазного асинхронного двигателя на статоре размещают вспомогательную обмотку, включаемую в сеть через пусковое сопротивление. В качестве такого сопротивления обычно используют активное сопро-

(3-12)

№йлёнйе или емкость; При эТоМ активное сбпроТивлбнйе МОже* быть либо внешним, либо внутренним (за счет выполнения вспомогательной обмотки из провода меньшего сечения или укладки бифи-лярных витков). Индуктивность в качестве пускового сопротивления применяется сравнительно редко. На рис. 3-12 даны векторные диаграммы токов в фазах двигателя при неподвижном роторе для различных типов пусковых сопротивлений. Как видно из диаграмм, при включении во вспомогательную фазу активного сопротивления или индуктивности фазовый сдвиг между токами и соответственно между НС всегда меньше 90°; это означает, что образуемое в двигателе магнитное- поле является эллиптическим; при включении во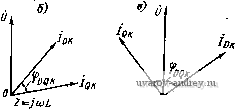

Рис. 3-12. Векторные диаграммы токов однофазного асинхронного двигателя при фазосдвигающем сопротивлении разного типа

вспомогательную фазу емкости можно в принципе подобрать ее значение таким образом, чтобы магнитное поле при пуске было круговым. Выбор способа пуска, значения пускового сопротивления и числа витков вспомогательной и главной фаз в однофазном двигателе представляет собой довольно сложную задачу, которая должна решаться с учетом заданных кратностей пусковых момента и тока, а также экономических затрат при производстве и эксплуатации двигателей.

Рассмотрим более подробно эту задачу для однофазного двигателя, у которого главная фаза занимает в два раза больше пазов, чем вспомогательная, а последовательно со вспомогательной фазой в общем случае включено

активное сопротивление Гн и емкость С (рис. 3-13). Пусть К = Q

да --коэффициент трансформации фаз Q и D (обмоточные коэффици-

еиты ko6Q и *об D принимаем равными); t = Sp/Sq - отношение площадей поперечного сечеиия проводов обмоток. Используя известные выражения для активного сопротивления обмотки и индуктивного сопротивления рассеяния, можно найти связь между этими параметрами фаз D и Q [21]:

г|=2/С<Гд; х1=2К^х^.

Здесь и в дальнейшем индексом сверху обозначены действительные (неприведенные) сопротивления, токи и напряжения фазы Q. Приведенное к фазе D полное сопротивление фазы Q будет

к

2XDS---

и, следовательно,

Z = - Zo = (2- l) .о + + / {xos - . (3-14)

Приведенные значения приложенных напряжений:

Ud = U; Uq=U/K. Для пускового режима (а = 0) сопротивления фаз прямой и обратной

последовательности равны между собой:

Df=ZjJi - Zjj; Zgf = Zqj == Zjr, + Z.

Подставляя эти значения в формулы (2-17), получим токи

и

L Zo

k{zd + z) J

L Zo

K{Zd+Z)

(3-15)

a затем no .формуле (2-19) при у = О - пусковой момент

Рис. 3-13. Электрическая схема однофазного двигателя с емкостью и пусковым сопротивлением во вспомогательной фазе

(3-16)

где Qi-jbi = \IZd - проводимость главной фазы в пусковом режиме;

- приведенная проводимость вспомогательной фазы в

Si - ibi =

Zd+Z пусковом режиме.

Из формулы (3-16) следует что, уменьшая коэффициент трансформации К, можно получить необходимое значение пускового момента. Однако следует иметь в виду, что значение К ограничено снизу значением пускового тока.

Отношение общего пускового тока к пусковому току главной фазы

-=1+.

= 1 +

K{za+Z)

=1 + -

k{\ + z]zd)

(3-17)

Dv. Dk

Совместное решение уравнений (3-16) и (3-17) позволяет иайти коэффициент трансформации и пусковое сопротивление. В общем виде эта задача неразрешима; для данного типа пускового сопротивления оиа может быть решена с помощью ЦВМ.

В ТОМ случае, когда параметры фаз D п Q двигателя известны, выбор пусковой емкости и пускового активного сопротивления можно сделать по одному из следующих параметров: максимальному пусковому моменту, максимальной добротности при пуске, заданному пусковому моменту или току.

Рассмотрим эту задачу для пусковых сопротивлений двух типов, применяемых на практике.

2п = п-

Емкостное пусковое сопротивление. Пусковые токи в фазах двигателя равны

/ QK =

RoK + ix

Qk + /{xqk~Xc)

где Rdk, лгок-и Rqk, atqk - активные и индуктивные сопротивления фаз D к Q, соответствующие режиму короткого замыкания

(S = 1).

(Согласно формуле (2-14) пусковой момент двигателя

Ма = KIdJqk sin <Pbq к,

где К' - постоянная величина, зависящая от параметров ротора.

Построим векторную диаграмму токов при пуске двигателя (рис. 3-14). Вектор тока главной фазы /дк отстает по фазе от напряжения на угол Фок, определяемый равенством

tg Фок = XdJRdk-

Конец вектора /qk при изменении сопротивления конденсатора Хс описывает окружность диаметром \AB\=UIRq; сам вектор /qk сдвинут по фазе от напряжения U на угол Фрк==

= arctg-~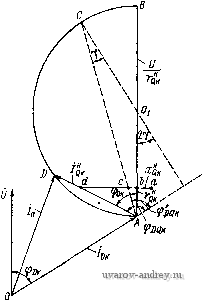

Для полу-

Рис. 3-14. Векторная диаграмма токов однофазного двигателя с пусковой емкостью

чения вектора /qk надо отложить вдоль диаметра окружности Л В отрезок А Ь, пропорциональный Rqk, перпендикулярно ему вправо отрезок Ьа, пропорциональный Xqh, и влево - отрезок ad, пропорциональный Проведя прямую из точки А через точку d до пересечения с окружностью в точке D, получим вектор /qk- Вектор 0D равен пусковому току, потребляемому двигателем из сети, /п = /ок + /ск-

Пусковой момент двигателя пропорционален /QкSinфoQк. т. е. длине перпендикуляра, опущенного из конца вектора /qk на вектор /ок. Максимальный момент соответствует такому емкостному сопротивлению хс, при котором этот перпендикуляр проходит через центр окружности 0, что соответствует точке С на круговой диаграмме. При этом

Это означает, что при максимальном моменте магнитное поле двигателя является эллиптическим. Емкостное сопротивление пропорционально отрезку ас и равно

Хс = 4к -f Rqvi tg V = 4к -f /?QK tg (я/4 -фок/2).

Если при пуске необходимо обеспечить максимальное отношение MJIn (максимальную добротность), это требование соответствует такой точке круговой диаграммы, в которой вектор /п касается окружности. Пусковая емкость в этом случае меньше, чем при максимальном моменте, так как соответствующее ей емкостное сопротивление (отрезок ad) больше. В общем случае при любом ус-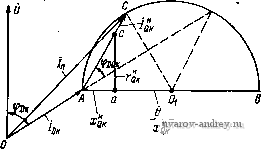

Рис. 3-15. Векторная диаграмма токов однофазного двигателя с активным пусковым сопротивлением

ловии пуска можно найти емкостное сопротивление так: определяем графически /qk для заданного требования при пуске, а затем находим

Активное пусковое сопротивление. Пусковые токи в фазах D и Q равны

Ок.-

и

Векторная диаграмма ТОКОВ изображена на рис. 3-15. При изменении сопротивления Гп конец вектора /qk описывает окружность диаметром U/xqk- Как и выше, пусковой момент пропорционален длине перпендикуляра, опущенного из конца вектора /qk на продолжение вектора /дк. Пусковой момент будет максимальным, если этот перпендикуляр проходит через центр окружности Qi-При этом

ф£ дк = Фок/2; Гп = х^к ctg (фок/2) - Rqk-

В общем случае в зависимости от требований при пуске можно графически найти пусковой ток фазы /qk, а затем

Q.=/{wrQ.У-xt и r =i?QK-/?K.

3-6. Конденсаторный двигатель

Двухфазный асинхронный двигатель, в одну из фаз которого постоянно включена емкость, называется конденсаторным. Для питания двигателя используется однофазная сеть переменного тока (рис. 3-16). Емкость и коэффициент трансформации обмоток иногда выбираются таким образом, чтобы в нормальном режиме работы фазовый сдвиг между токами составлял 90° и в машине было образовано круговое вращакхдееся магнитное поле.

Рассмотрим условия, при которых магнитное поле в конденсаторном двигателе будет круговым. Обозначим Zd - Гр + jxo - полное сопротивление фазы D; Z = Zl- /дг - неприве-денное полное сопротивление фазы Q;

-коэффи-

циент трансформации. Тогда

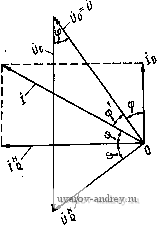Рис. 3-16. Электрическая схема конденсаторного двигателя

Рис. 3-17. Векторная диаграмма токов и напряжений конденсаторного двигателя

Tq - /CVд; jiq = }(Хр\

tg фо = tg фQ = tg ф = Xolro = х\1г\\

(3-18)

Векторная диаграмма токов и напряжений, соответствующая круговому магнитному полю в машине, изображена на рис. 3-17. При построении векторной диаграммы следует учитывать, что токи в фазах двигателя /д и 1\ отстают по фазе от соответствующих напряжений на угол ф, а напряжение на конденсаторе Щ отстает рт тока 1\ иа 90°. Для получения кругового поля токи /д и Iq

должны быть сдвинуты по фазе на 90°, а соответствующие им НС /дШоКобо = -№оКобс или Io==-jIK- (3-19) Из векторной диаграммы находим и c=Uq/sin (f;

;H 7НГН

1/D DD Л

(3-20)

Реактивная мощность конденсатора, определяющая его габа. риты, Рс = UcIq. Отнощение ее к полной мощности S, потребляемой двигателем, будет

(3-21)

Ток, потребляемый конденсаторным двигателем из сети, / = /d + /q = /d(H- K);

sin ф

(3-22)

Из треугольника токов на рис. 3-17 находим ф' + ф + ф = я/2; отсюда коэффициент мощности конденсаторного двигателя

cos ф'=со8 - 2ф^ = sin 2ф.

(3-23)

Соотношения (3-20) определяют условия получения кругового поля в двигателе, которые для заданных параметров двигателя, зависящих от скорости ротора, могут быть реализованы при вполне определенных значениях емкости и коэффициента трансформации. Следует отметить, что коэффициент трансформации, относительная реактивная мощность конденсатора и cos ф' конденсаторного двигателя зависят только от фазового сдвига между током и напряжением симметричного двигателя.

На рис. 3-18 приведены зависимости этих величин как функции коэффициента мощности симметричного двигателя. Практическое значение имеет область, находящаяся в пределах 0,7<cos ф<0,9. При COS Ф = 0,707 двигатель потребляет из сети только активный ток (cos ф' = 1). Относительная мощность конденсатора тем больше, чем выше cos ф двухфазной машины. Поэтому с точки зрения стоимости конденсатора желательно иметь более низкий cos ф. Однако

снижение cos ф за 0,707 нецелесообразно, так как мощность конденсатора уменьшается незначительно, а cos ф' - сильно.

Расчет пускового момента и механической характеристики при пуске двигателя можно выполнить методом симметричных составляющих (см. § 2-2). Токи прямой и обратной последовательности получим из (2-17) при О о = = и я Uo = UlK:

110=и

ZofZQb + ZDbZqf

f TJ ZQf±JZDflK

bc - U --------,

OfQb + Zob-Qf

(3-24)

причем Zdj, ZDb, Qf> Qb определяются no схемам замеще-

Рис. 3-18. Зависимость К, PdS и cos ф' от коэффициента мощности симметричного двигателя

COSf

W 0,8 0,6

0,2 О

0 0,2 Ofi 0,6 0,8 cos

ния, приведенным на рис. 2-7, если в них Zq заменить на Zd -

Подставляя выражения для токов (3-24) в формулу (2-19), находим

Шс 1 ZDfZQb -f ZDbZQS f

Zqb-iZoblf rRl-v)

\ZQf + iZDf/K\rKl + v)

(3-25)

Расчет момента по формуле (3-25) можно выполнить с помощью ЦВМ.

Из формул (3-24) нетрудно найти выведенные выше условия получения кругового вращающегося поля при включении емкости во вспомогательную обмотку. Поле будет круговым, если Дс = О

или Zqi + jZDflK = 0.

Подставляя сюда значения Zq/ и Zof, соответствукщие схемам, приведенным на рис. 2-7, получим

Отсюда

К = XdITo, X с = TdK -]-XdK = Xd-\- Xq,

что совпадает с (3-20), так как

Следует otMefHtb, 4t6 МаЛоМощйыё KoнДeнcatopHЫe ДВИГаТеЛи часто работают при переменной нагрузке и скорость их изменяется от номинальной до скорости холостого хода. В этом случае выбор емкости из условия получения кругового магнитного поля в номинальном режиме может привести к возрастанию потерь в режиме холостого хода и перегреву двигателя; это объясняется значительным ростом напряжения на фазе Q в режиме холостого хода и потерь от токов обратной последовательности. Для определения! емкостного сопротивления и коэффициента трансформации при переменных нагрузках следует исходить из допустимых потерь двигателя в режиме холостого хода и под нагрузкой. Зная параметры главной фазы, определяем отношение потерь в двигателе к электромагнитной мощности V = = ДР/Рэм и строим в координатах хс, К зоны равных потерь, т. е.зоны, внутри которых АР отличается от соответствующего значения при круговом поле на заданную величину. На рис. 3-19 в качестве примера приведены зоны равных потерь двигателя 180 Вт, 1500 об/мин; в номинальном режиме (s = 0,05)- - сплошные линии, в режиме холостого хода - штриховые. ки - точка, отвечающая круговому полю; этой точке соответствует увеличение потерь в режиме холостого хода для данного типа двигателя на 15 %. Если допустить увеличение потерь в машине для обоих режимов на 5 %, то получим значения хс и Л', соответствующие точке МП (минимальные потери). При этих значениях емкости и коэффициента трансформации поле в номинальном режиме отличается от кругового, а пусковой момент несколько уменьшается.

На практике пользуются следующей рекомендацией: если двигатель спроектирован для получения кругового пол? в номинальном режиме, то для его работы в режиме холостого хода емкость выбирают, исходя из получения кругового поля при скольжении, соответствующем номинальной нагрузки. .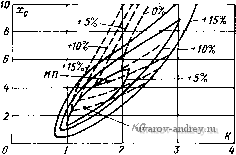

Рис. 3-19. Зоны равных потерь конденсаторного асинхронного двигателя

3-7. Универсальный асинхронный двигатель

Асинхронные двигатели, рассчитанные для работы от сети как трехфазного, так и однофазного переменного тока, называются универсальными асинхронными двигателями (УАД). Эти двигатели имеют симметричную трехфазную обмотку на статоре и коротко-замкнутый ротор типа беличья клетка . Обмотка статора имеет 6 выводных концов. При работе двигателя от трехфазной сети его обмотки статора соединяются звездой; в этом случае режим работы двигателя симметричный, соответствующий круговому вращающемуся полю. В однофазную сеть двигатель обычно включается по схемам, приведенным на рис. 3-20.

Первая схема (рис. 3-20, а) фактически равноценна схеме двухфазного конденсаторного двигателя (см. § 3-6), в котором фаза D состоит из двух фаз В и С трехфазного двигателя с числом витков

а)о = 2а)ф|/3/2 = ШфУТ, а фаза О есть фаза А трехфазяого двигателя с числом витков = Шф. J<oэффициeнт трансформации фаз D и Q равен К = о'д/о'о = 1/13 . Согласно формулам § 3-6, условиями получения кругового поля при включении емкости в фазу А будут

1) tg9 = /<= l/j/S или ф = ЭО°,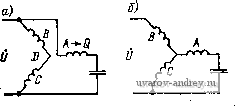

Рис. 3-20. Схемы включения обмоток статора трехфазного двигателя в одиофазиую сеть

что соответствует cos Ф == 0,866 трехфазной машины, и

2) *с =

2ф

:22ф.

Реактивная мощность конденсатора V cos Ф / же

(3-26)

хс Ч COS Ф у хс згф Расчет характеристик даигателя при работе от однофазной сети можно выполнить методом симметричных составляющих [21]. Найдем сопротивления прямой и обратной последовательности фаз D и Q. Обозначим: Тф, х^, Хт - активное сопротивление, индуктивное сопротивление рассеяния фазы трехфазной обмотки, индуктивное сопротивление намагничивания; Гр, Xps - активное сопротивление и иидуктивиое сопротивление рассеяния обмотки ротора, приведенные к фазе трехфазной обмотки статора. .,

Коэффициент приведения сопротивлений ротора к двухфазной обмотке с числом витков главной фазы D

= 2.

Аналогично коэффициент приведения сопротивлений ротора к вспомогательной фазе Q

2 3

Параметры схем замещения фаз D и Q, полученных соединением трехфазной обмотки по схеме рис. 3-20, а. будут: Го = 2гф - активное сопротивление фазы D; хр = 2 дсф, - иидуктивиое сопротивление рассеяния фазы D.

= ( о/®!) *т = 3*т ~ сопротивление взаимной индукции фазы D; Грр= К5*р'р= 2Гр -активное сопротивление ротора, приведенное к фазе D; ХрР= Kx, = 2xt~ индуктивное сопротивление рассеяния ротора,

3 Заказ М 678