Однако и в этом случае выражение для момента машины при произвольных приложенных напряжениях оказывается достаточно сложным.

Расчет характеристик двухфазной асинхронной машины может быть выполнен по схеме, соответствующей уравнениям'ЭДС в осях d ¥1 q. Для получения этой схемы запишем уравнения ЭДС в явном виде, полагая 0=0 = 0:

JXmid-vxJq + {r + jx) ii-vxig = 0;

VXmiD + iXmlQ + VXla + {г + jx) / = 0.

(1-18)

/7+v

% 5 f? jOq

Рис. 1-7. Схема замещения неявнополюсной электрической машины переменного тока

Преобразуем третье и четвертое уравнения, исключив из них

токи Id и Iq. Умножая четвертое уравнение на - jv, складывая его с третьим и деля на 1-гг*, получим

Умножая третье уравнение (1-18) на jv, складывая с четвертым и деля на 1-гг*, найдш

Заменяя х на x+Xs, а

1-1+0 1 у2

жая второе уравнение (1-18) на /, окончательно получим

/ Uq = (Zq + jx )jiQ + jxJIq.

И умно-

(1-19)

Нетрудно видеть, что этой системе уравнений соответствует схема замещения, изображенная на рис. 1-7. При v = О схема замещения распадается на две независимые схемы фаз D к Q, соответствующие режиму короткого замыкания.

Следует отметить интересную особенность схемы замещения. Токи в контурах q к Q сдвинуты по фазе на 90° по отношению к действительным токам в обмотках. Физически это объясняется тем, что электрическая связь между схемами замещения двухобмоточных трансформаторов по осям D и Q происходит через контуры ротора Вид из-за ЭДС вращения. Но ЭДС вращения сдвинута по фазе относительно трансформаторной ЭДС на 90°; поэтому для

Рис. 1-8. Преобразованная схема замещения неявнополюсной электрической машины переменного тока

согласования падений напряжений в схеме замещения необходимо токи в контурах 9 и Q также повернуть на 90°, т. е. умножить на /.

Если звезду активных сопротивлений на рис. 1-7 преобразовать в треугольник по известным формулам, то получим схему замещения двухфа.9-нон асинхронной машины, изображенную на рис. 1-8.

1-3. Исключение неизвестных токов из уравнений ЭДС

При определении токов и момента в электрических машинах переменного тока в некоторых случаях целесообразно уменьшить число неизвестных токов путем исключения их из уравнений ЭДС. Так, например, для асинхронного тахогенератора (см. § 7-4) нет необходимости вычислять токи в короткозамкнутом роторе, а при расчете механических характеристик управляемого двигателя- токи в статоре. Исключение токов статора или ротора наиболее просто выполняется при матричной форме уравнений ЭДС. Уравнение ЭДС обобщенной электрической машины запишем в развернутом виде

(1-20) 27

Введем двухмерные векторы токов и напряжений статора и ротора и матрицы сопротивлений в соответствии с разделением, выполненным штриховыми линиями в уравнении (1-20):

2i =

DV ro + jxD 0

QL о rq+jXQ J

J-md Хщ

- Xmd JXtng

jXmd 0

JXttlg -

Я

r+JXg J

Тогда уравнение (1-20) запишем в виде двух матричных уравнений

которые могут быть сведены к одному уравнению относительно токов статора или ротора.

Исключим токи статора. Из первого уравнения (1-21) находим

/i = Z7t/i-Zl Zg/a,

где Zr - матрица, обратная по отношению к Zy.

Подставляя вектор тока /1 во второе уравнение (1-21), получим

[Z-ZZT%) 1\ = U,-Z,ZTUr

или

Zih = U2. (1-22)

где Zi = Zi-ZgZrZj - матрица переходных сопротивлений ротора; и'2 = t/2-ZgZrf/i - новый вектор приложенных к ротору напряжений.

Используя выражения для Z, Z, Z3, Z4, получим для определения токов ротора матричное уравнение

r + jxdii) VXd (j)

Я

- XgiJ) r+JXgiJ)

Ud + Ed + ivEg

L Ug+Eg-ivEd J

где Xd(j) = Xi-

XgiJ)=Xg -

(1-23)

переходные co-

противления фазы ротора по продольной и поперечной осям;

D.e=~Q-трансформаторные ЭДС, ин-

дуцируемые в фазах ротора (здесь и в дальнейшем индекс тр у трансформаторной ЭДС будем для упрощения записи опускать);

jvE - jvEd - ЭДС вращения.

Уравнение (1-23) показывает, что после исключения токов статора вид уравнений ЭДС для ротора не изменился. Однако параметры ротора стали переходными, они определяются с учетом воздействия короткозамкнутых контуров статора. Кроме того, в цепях ротора появились трансформаторные ЭДС и ЭДС вращения, которые индуцировались бы в роторе при разомкнутых его обмотках. Электрическая схема полученной двухобмоточной машины представлена на рис. 1-9. Рассмотренное преобразование является аналогом известной из теории электрических цепей теоремы об эквивалентном источнике тока.

Можно показать, что после исключения токов статора выражение для момента также сохраняет свой вид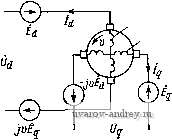

Рис. 1-9. Электрическая схема двухобмоточной машины с исключенными контурами статора

iW = -i?e(/p2); (l-4)

ш

здесь Ва - вектор индукции, составляющие которого получаются из матричного уравнения 24/3 - Уг = О как члены, содержащие множитель о. Из уравнения (1-23) находим

- Xq (/) / - jEq

L xd{j)id + jEd

Подставляя в (1-24) значения 1 и В^, получаем

Л1 = - Re [ - jEq и + lEd fq - Xq (/) /, /<г -f Xd (/) h Iq] (1-25)

Аналогично производится исключение токов ротора, и уравнение для контуров статора принимает вид

Z\i = u\, (1-26)

где Z, = Z-ZjZZj - матрица переходных сопротивлений статора; U\ = = t/,-ZZt/j - вектор приложенных напряжений.

В качестве примера исключим токи ротора из уравнений ЭДС неявно-полюсной электрической машины с короткозамкнутым симметричным ротором, матрица сопротивлений которой определяется формулой (1-16). В этом случае

D Q d q

О

3 = Хт

Zd + JXm О D

d г / q L V

Zq + iXm J

Za = jx

- V I J

Z4 =

r -j- ]x - vx

r+ jx J

q L vx

[г + ixf - q

- r + ix

. -vx

r + jx

Подставляя эти выражения в формулы для Zj и (Уj, получаем D Q

2 r + j{l-V)x

(r + jxf + vV

iXmrv

(r + jx) + (Г + jx) + Ц^ДГ

U[ = U =

Ud L ()q j

1-4. Преобразование уравнений ЭДС и момента

Уравнения ЭДС и момента большинства электрических машин можно получить из уравнений ЭДС обобщенной машины путем стандартной операции-преобразования токов обобщенной машины к токам реальной машины. Это преобразование может включать в себя поворот обмоток, соединение их между собой, переход от токов в ветвях к контурным токам, переход к симметричным составляющим и т. п.

Обозначим через С матрицу, определяющую преобразование токов реальной машины / к токам обобщенной электрической машины /:

(1-27)

Закон преобразования напряжений и матрицы сопротивлений установим из условия инвариантности мощности

и =и'с или и'С'и- (1-28)

Преобразуем уравнение ЭДС обобщенной машины в матричной форме

V =Zl =ZCI-

Умножив левую и правую части уравнения на матрицу С^, получим

где

Z =CZC.

(1-29)

Формулы (1-28) и (1-29) определяют искомый закон преобразования вектора напряжений и матрицы сопротивлений. В том случае, когда матрица С содержит комплексные числа, например при. переходе к симметричным составляющим, формулы преобразования вектора напряжений и матрицы сопротивлений имеют вид:

Ь =с'(1;

Z = CZC-

(1-30)

Совершенно аналогично преобразуется вектор индукции В и матрица момента G, которая состоит из элементов матрицы сопротивления Z, имею-

щих в качестве множителя угловую скорость ротора (Ор = уш;

в' = с' в; g=cgc- (1-31)

Выражение для момента через новые токи сохраняет свой вид

= - Ц^{В') = Re (/ G/ ). (1-32)

В качестве примера рассмотрим работу репульсионного двигателя в установившемся режиме. Схемы двигателя (а) и соответствующей ему модели обобщенной машины (б) представлены на рис. 1-10.

Матрица преобразования токов

D Г 1

q I О

О П

cos а sin а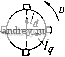

Рис. 1-10. Схема репульсионного двигателя

Матрицу сопротивлений обобщенной машины получим из выражения (1-16), опустив строку и столбец, соответствующие контуру Q:

D d q

IXm о

hm r + jx - VX

VXm VX r + jX J

Матрицу сопротивлений репульсионного двигателя найдем по формуле

Z = Cfzc.

Выполняя вычисления, получаем

D г го + 1хт

Z = d

ZC =d

2 = CZC =

+ IXm fXm COS a

Ixm (r -f jx) COS a - ал: sin a

VXm VX COS + (/ + jx) sin a .

D Г Zo + iXm jXmCOsa

L - т (/COS a + a sin a)

r + ix

Для определения токов репульсионного двигателя найдем обратную матрицу

D п

(Z)-i -L

+ ix

- jXm COS a d + iXm

где Д - определитель матрицы Z. Отсюда

г + jx

Д n L -- тС/cos a-1-е sin a)

A L - (i cos a + D sin a) итель матрицы Z.

/ = (Z)-W =

Выражение для момента найдем по формуле (1-32), в которой G = = Хт sin а.

Подставляя сюда токи /д и / , получаем

} * }

М = - Ке(/ л: 5ша/о) = - со со

ирХт (/ COS а - а sin а)

X Хт sin а

{г + 1х)ир 1 D4sin a А J cuJAp

Таким образом, окончательно имеем

Re [ (/ COS а - а sin а) (г -f jx) ].

U\,xl,sma

М =--(л: cos а + sin а).

со \\

Знак минус означает, что для положения щеток, указанного на рис. 1-10, а, момент двигателя направлен в сторону, противоположную принятому направлению вращения ротора.

1-5. Неявнололюсная четырехобмоточная

электрическая машина

с малой асимметрией магнитопровода

Погрешности высокоточных электрических микромашин: вращающихся трансформаторов, сельсинов, асинхронных тахогенераторов, двухфазных управляемых двигателей и др.- существенно зависит от асимметрии магнитопровода, появляющейся от неточности изготовления машины. Для приближенной количественной оценки этой зависимости рассмотрим электромагнитные соотношения в машине с асимметричным магнитопроводом при условии, что асимметрия невелика.

Физическая модель машины. В симметричной идеализированной неявнополюсной машине магнитная проводимость Х^, соответствующая воздушному зазору и магнитопроводам статора и ротора, постоянна и не зависит от выбора оси, вдоль которой она определяется. В несимметричной машине, имеющей неравномерный зазор, короткозамкнутые витки в магнито-проводе, асимметрию в магнитных свойствах пакетов и т. п., магнитная проводимость X не остается постоянной. При малой асимметрии ее можно представить в виде

где ДА, - относительное изменение магнитной проводимости, обусловленное малой асимметрией, которое зависит от выбора направления НС обмотки.

Введем для машины систему координат d к q, совпадающую с осями обмоток статора, и определим магнитные проводимости по этим осям и i.q при наличии произвольной, но малой асимметрии магнитопровода (рис. 1-11). Положим, что по оси d действует НС Fd= I А; создаваемый ею магнитный поток представим в виде

Ф = Ф<г + A<i>d + dq,

где - магнитный поток симметричной машины; Аф и Аф,- добавочные магнитные потоки, появляющиеси по осям d н q вследствие магнитной асимметрии.

Соответственно магнитную проводимость по оси d можно представить в виде

id = /Fd=-h(.l + d + df), (1-33)

где ДХ. - относительное изменение магнитной проводимости по оси d; 32

д^ относительное изменение магнитной проводимости взаимной индук-

цим'd к q из-за асимметрии магнитопровода. нитная проводимость по оси q

Аналогично определяется маг-

К = ф/f = (1 + д + AXqd):

(1-34)

очевидно, что А \dq = \d-

Сформулируем основные допущения для физической модели неявнополюсной электрической машины с малой асимметрией магнитопровода; 1) магнитные свойства магнитопровода характеризуются проводимостью симметричной машины и относительными изменениями комплексных магнитных проводимостей А id, А Я. А %dq, зависящими от асимметрии магнитопровода, выбора реей d к q к угла поворота ротора;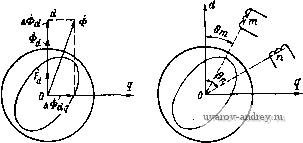

Рис. 1-11. Магнитные по- Рис. 1-12. Электрическая схе-

токи в электрической ма- ма асимметричной машины

шине при асимметрии с произвольно расположен-магнитопровода ными обмотками статора

2) на статоре и роторе машины расположены две взаимно перпендикулярные, синусоидально распределенные обмотки;

3) параметры обмоток постоянны и не зависят от углового положения ротора;

4) все приложенные напряжения и токи являются синусоидальными функциями времени; это позволяет все величины, характеризующие электромагнитные процессы, изображать в виде комплексных величин.

Матрица иидуктивиостей. Определим комплексную взаимную нндук-тивность двух произвольных обмоток тип, составляющие углы 9 и 9 с осью d (рис. 1-12).

Пусть по обмотке п протекает ток 1 А; тогда составляющие НС, магнитных потоков и потокосцеплений по осям dn q с учетом формул (1-33) и (1-34) можно записать в виде:

По оси d Fn - -Wn cos 9 .Xe[(l-f A!.<i)cos9 -f + AXdq sin 9 ] Wn

. .XoWmWn[0 + d)X X cos 9 cos 9m + A\dq sin 9 cos Qm] 2 Заказ Ni 678

По оси q WnSin 9

[(H-A)sin9 + -f Aiq cos 9 ] w

hWmWn [(l + iq)X

X sin 9 sin 9m -f Akdq cos 9 sin Bm]

Отсюда ч1аходим комплексную взаимную индуктивность обмоток тип. im = io [ (1 + А id) cos 9 cos 9 -f (1 + А д) sin е„ sin9 +

+.AXd sin(e + 9 )], (1-35)

где Lg = AgWmWn.

Эта формула позволяет записать матрицу взаимных индуктивностей при любом расположении обмоток на статоре и роторе по отношению к осям d ц q. Наиболее простой вид матрица взаимных индуктивностей имеет для машины, обмотки которой на статоре и роторе совпадают с осями d и q:

Z. = Le

(1-36)

Уравнения ЭДС, матрицы сопротивлений и проводимостей. Будем считать, что собственные параметры вторичных обмоток одинаковы, а токи и напряжения их приведены к осям D и Q. Уравнение ЭДС при неподвижном роторе запишем в виде

(Ze-f AZ)/ = i/, (1-37)

где векторы тока и приложенного напряжения

Yq = iQ? - безразмерные параметры об.

моток D и Q; Va = llLi безразмерный параметр обмотки ротора (якоря).

здесь vo = ±i;

AZ = jXm

- добавочная матрица сопротивлений, появляющаяся вследствие электромагнитной асимметрии магнитопровода и обмоток.

Решение уравнения (1-37) найдем н приближенном виде

/ = /o-fA/, (1-38)

где = ZU - ток идеализированной симметричной машины.

Подставляя выражение (1-38) в уравнение (1-37), получаем (пренебрегая произведением AZAI)

ZqAI + AZZU = 0; А/= -ZAZZ-Ю = AYU. AY= - ZTTAZZZ

(1-39)

Матрица

ZoAZZ\ (1-40)

может быть названа матрицей проводимости для определения изменений токов в асимметричной машине по сравнению с соответствующими токами в идеализированной машине. Матрица проводимостей идеализированной симметричной машины имеет вид

0 -

D 1+Уа

О

О

Q О

1+Ya О

YaO О

Я О

1+yo

УаЬ О

О

1+y(?

где

YflO = Ya + YO + YaYo: YaQ = Ya + Y + YoYq-

По формуле (1-40) находим матрицу

АК =--- X

YaoYaQ YgYp Yd VaYQ

YaoVflQ

AXde

Aide

- AYd?

YaYQ

Л2 AX, YaQ

VgYg YaoVaQ

yL ydyq

- Aidg

-Akdg

- Aktla

VaoYaQ YaQ

-Akdg

A. УаЯ

(1-41) 35

с

ввод исходных данных (чисел)

Подготовка массива, под матрицу сопротивлений

Приведенные выражения позволяют по известным относительным нз-мененням магнитных проводимостей определить токи и ЭДС, появляющиеся в контурах асимметричной машины, и оценить таким образом технологические погрешности, а также связь между различными величинами, характеризующими эти погрешности. Более подробно этот вопрос рассмотрен в § 9-8 для двухполюсных вращающихся трансформаторов.

1-6. Анализ обобщенной электрической машины переменного тока с помощью ЦВМ

Точность результатов исследования определяется рядом факторов: совершенством физической модели (основными допущениями), объективностью и достоверностью исходных данных, возможностями применяемого математического аппарата и т. д. Уточиеиие физической модели, как правило, приводит к услвжнеиию математической теории (модели) изучаемого объекта или явления. Матричное представление уравнений электрических машин являетея весьма эффективным средством для анализа их характеристик. Однако с увеличением числа рассматриваемых контуров электрической машины или системы машин резко возрастает трудоемкость решений. Если при записи уравнений желательно учесть все лектрические параметры или некоторую асимметрию машины, то решение в общем виде усложняется еще больше.

Наличие комплексных величин в исходных уравнениях обусловливает комплексный характер получаемых выражений, что ухудшает их обозримость и физическую интерпретацию.

Из вышесказанного следует вывод о целесообразности поиска иных методов анализа характеристик электрических машии. Одним из таких методов является численный анализ с примеиеиием ЦВМ. Современные вычислительные машины обеспечены большим набором стандартных программ для решения наиболее типичных задач. К таковым относится решение систем вл-гебраических уравнений с действительными коэффициентами (есть стандартные программы для решении систем линейных уравнений 20-го, 50-го и более высокого порядка). Алгоритмический (входной) язык альфа-системы содержит описание действий над комплексными числами и позволяет программировать решение комплексных матричных уравнений, что очень важно для задач электромеханики.

Рассмотрим методику численного анализа с применением ЦВМ иа примере следующей задачи: определить зависимость механических характеристик, потребляемой мощности и мощности на валу обовщениой электриче-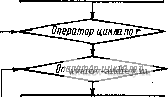

Вычисление эшенипв изапшение матриц

Расчет токод

Расчет М, Р., и Pi, как функций vur

Заполнение и вывод на печать массива результатов

Конеи, решения

Рис. 1-13. Алгоритм расчета

ской машины, уравнение которой имеет вид

Uq 0

(1-42)

L 0 J

от активного сопротивления ротора г. Формулы для вычисления момента М, потребляемой мощности Pi и мощности на валу Pj известны, а именно

М

/ * * * * \

Re \ - Xmqidig - XqIdlq -V XmdlqID + xjlqld);

Pi= ReilDUD + IqUQ);

P2=M(0cV,

(1-43)

где (Dg = 2nfjp; fi - частота питающего напряжения; p - числе пар по-люсов; V - относительная скорость ротора (в долих синхронной Юс)-

1. Уточнение условий задачи и исходных данных. Для решения аадач* численным методом необходимо все величины и коэффициенты в фуиквдо-иальных зависимостях, входящих в математическую модель, выразить через исходные даииые. Аиалиа зависимостей Л1, Pi и Pj от и и г будем проводить при известных электрических параметрах машины и определенных напряжениях Ud и Uq, т. е. численные значения сопротивлений контуров машины и иапряженнй должны задаваться как исходные данные. Переменные V и г задаются минимальным значением, максимальным и шагом изменения.

2. Выбор численного метода. Значения М, Pi и Рг могут быть вычислены по формулам (1-43), если определить токи из уравнения (1-42). В альфа-системе предусмотрена стандартная программа для вычисления детерминанта матрицы с комплексными элементами. Поэтому токи /д, Iq, Id Iq наиболее просто находить с помощью детерминантов соответствующих матриц.

3. Алгоритм решения удобно представить в виде схемы (рнс. 1-13).

Главв вторая

АНАЛИЗ ДВУХФАЗНЫХ МАШИН

МЕТОДОМ СИММЕТРИЧНЫХ СОСТАВЛЯЮЩИХ

2-1. Образование вращающегося магнитного поля в двухфазной машине

Рассмотрим неявнополюсную электрическую машину, на статоре которой расположены Две обмотки (фазы), оси которых сдвинуты на угол а (рис. 2-1). Положим, что магнитное поле, создавае-

мое каждой из обмоток, имеет синусоидальное распределение в воздушном зазоре, а токи в обмотках сдвинуты по фазе на некоторый угол р.

Выражения для индукции магнитного поля фаз D и и запишем в виде

Jd = BDmsin(pcos(o<;

Вп = Влт sin (ф -1- а) cos {Ы + р),

где ф - угол по расточке машины, отс итываемый от линии, перпендикулярной оси фазы D. Разложим пульсирующие поля Bp и

Вп на два, бегущих в противоположные стороны.

Во= Ват sin (ф- Ы) +

+ - Вот sin (ф-f ©0; Вп = - Впш sin (ф- (о< + а-р) +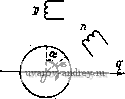

Рис. 2-1. Щеявиаполюс-иаи электрическая ма-ш'йиа с йеперпеидику-ляриымй обмотками ста- тора

+ -В т8т(ф + (о/ + а+р)

И сложим поля, вращающиеся в одном направлении:

B-.Bд + B = Bf sin(ф-ю^-у) + Вбт8т(ф + (о/ + 8), (2-1)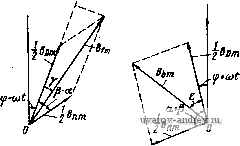

Рис. 2-2. Векторные диаграммы для определения Bf и Bj

где индексом / обозначена индукция поля, вращакмцегося в прямом направлении (против часовой стрелки), а индексом b - индукция поля, вращающегося в обратном направлении.

Значения В^ , Bj , у и г находим из векторных диаграмм, изображенных на рис. 2-2:

Bfm = ~ [Вот + BL + 2ВотВ COS ф-о)] : (2-2)

Вьт = [Вк + BL + 2Bd B cos Ф + a)f; (2-3)

tgv =

Bnm sin (Р -а)

В Dm + Впт cos ф -a)

; tge =

g sin(P + a)

Bcm-f B mCOS(p-f a)

(2-4)

Таким образом, в общем случае при произвольных значениях В Dm, В„т, а и р магнитное поле двухфазной машины состоит из двух полей, вращающихся в противоположные стороны со скоростью (О = dff/dt. Магнитное поле в воздушном зазоре будет круговым, если Bjm = О-

Из формулы (2-3) находим условия получения кругового поля

Вот^Впт) а + р:=я. (2-5)

Максимальная индукция прямого кругового магнитного поля при этом

Bfm = 4- BDmK2[l + cos(p-a)] = ВдcqS .

угол у определяется формулой

tgV:= Sin(P- )

1 -f COS (Р - а)

Подставляя сюда значение р из (2-5), находим B/m = BomSina; tgyctga.

(2-6)

Для двухфазных машин со взаимно перпендикулярными обмотками Ь и Q для получения кругового магнитного поля необходимо

BDmBprn, Р = а=л/2.

(2-6а)

При этом Bfm = Вот; Y = 0.

Если условия (2-5) не выполняются, то конец результирующего вектора индукции магнитного поля описывает эллипс. Действительно, совместим с осью фазы п ось у декартовой системы координат Oyz (рис. 2-3); тогда

By = Впт cos (<о^-Р) -f Вот COS а cos at = В'пт COS {at- у');

Вг = Вот sin а COS at = В'от COS at,

где у'- некоторый угол.

Полученные уравнения представляют собой известные из курса математики уравнения эллипса в параметрической форме. Следовательно, в общем случае при любых значениях а и Р магнитное поле электрической машины является эллиптическим вращающимся магнитным полем и только в частных случаях, указанных выше, оно превращается в круговое вращающееся магнитное поле.

Очевидно, что спраьедлйЁо й обратное утверждение: эллиптическое магнитное поле можно разложить на два круговых магнитных поля, вращающихся в противоположные стороны. Совместим оси координат с главными осями эллипса (рис. 2-4). Построим две окружности с радиусами, равными полусумме и полуразности полуосей эллипса

В

1т

В

(2-7)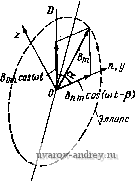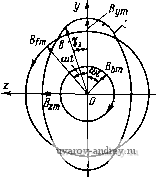

Рис. 2-3. Эллиптическое Рис. 2-4. Представление эл-магнитное поле липтического магнитного

поля в виде двух круговых, вращающихся в противоположные стороны полей

Положим, что вектор В^ вращается против часовой стрелки и является прямым круговым вращающимся полем, а вектор В^т вращается по часовой стрелке и является обратным круговым вращающимся полем. Уравнения этих полей запишем в виде уравнений окружностей в параметрической форме:

для прямого поля

% = 5/т COS ю/; fifz = flfm sin (0;

для обратного поля

ьг/ = Ып cos (- (dt) = Вьт COS (o/; fl42 = flbmSin(-{О0= -fifcmSin (nt.

Составляющие суммарного поля будут

5J/ = 5f+ fifcj, = (5/m + flfcm ) COS (о/; = flf г +Вьг= {Bfm - fifcm) Sio Uyt.

Исключая отсюда время, получим уравнение эллипса в координатах yz

= 1.

(2-8)

(В,т + Вьш? (Bfm-Bbmf

Т. е. дйа круговых вращающихся поля эквивалентны эллиптическому вращающемуся полю.

В заключение найдем угловую скорость вектора индукции эллиптического магнитного поля. Из рис. 2-4 определяем угол Уэ, образуемый вектором В и осью у:

(Вfm + Вьт) cos Ы

эллиптичности магнитного

где = - - коэффициент

Bfm + Вьт

поля. Отсюда

V3 = arctg(*3tg (at)

dt l+lii t(ot cosat Выполняя элементарные тригонометрические преобразования,

получаем

l (l ;)sin2u)<

(2-9)

Из формулы (2-9) следует, что угловая скорость вектора индукции эллиптического магнитного поля является переменной и изменяется от минимального значения эю (при со = О и 180°) до максимального (о/кз (при = 90 и 270°).

2-2. Метод симметричных составляющих

Для анализа несимметричных режимов электрических машин переменного тока широко применяется метод симметричных составляющих, при котором токи и НС в машине заменяются двумя системами токов и НС прямой и обратной последовательности, образующими круговые магнитные поля с противоположными направлениями вращения. Рассмотрим сущность этого метода применительно к двухфазной неявнополюсной машине с взаимно перпендикулярными обмотками D и Q и симметричным короткозамкнутым ротором (рис. 2-5). Пусть Fo Pq - комплексные НС этих обмоток. Представим эти в общем случае неравные векторы, сдвинутые по фазе на произвольный угол р, каждый в виде суммы двух одинаковых векторов, сдвинутых на 90° (рис. 2-6, а):

FDFof + Fpf,; FQ = FQf+F(b

при этом

Вектори Fof и Fq; образуют поле, вращающееся против часовой стрелки; они называются составляющими НС прямой последовательности. Векторы Fob и Fq образуют поле, вращающееся по часовой стрелке, и называются составляющими НС обратной последовательности. Обозначая для краткости Fof = Ff и Роь = /ь, приведенные выше выражения записываем в виде

Fo = F, + F,; FQ = j{Ff-F,).

О

Рис. 2-5. Электрическая схема двухфазной неявно, полюсной машины с короткозамкнутым ротором

р Рр + JFq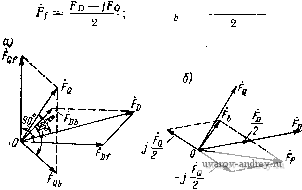

Рис. 2-6. Несимметричная система НС (а) и ее симметричные составляющие (б)

Векторы Ff и f J НС прямой и обратной последовательности легко могут быть получены графически, как это указано на рис. 2-6, 6: Аналогичные соотношения могут быть получены для токов. Считая параметры обмоток и токи приведенными к фазе D, имеем

tf- 2 . h----

Уравнения напряжений для фаз D и Q .запишем в виде

и D = Zofl Df + Zobf Dt QQflQf + ZQblQb-

(2-10)

(2-11)

Здесь Zof, Zob и Zqf, Zqj, - сопротивления фаз D и Q соответственно для симметричных токов прямой и обратной последовательности. Они определяются по обычным схемам замещения симметричной индукционной машины (рис. 2-7). Заменяя lof на /f, 1оь naif .!of на jlf и Iq на - /Д, уравнения (2-11) записываем в виде

Dfif+Dbh - Di

-ZQfif+ZQJ.jUQ.

mri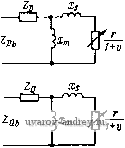

Рис. 2-7. Схемы замещения для определения сопротивлений прямой и обратной последовательности обмоток D и Q

Решая их относительно токов If и находим

/ == Qb D iDbOQ . DfQb -f ZobQf

J ZQfUp -f jZpfUQ

ZoJQb -{-DbQb

(2-12)

Электромагнитный момент машины найдем как разность моментов, создаваемых токами прямой и обратной последовательности-

М = М,-Мь.= -(Рщ-Рэь),

12-13)

где Paf, Рэь - мощности, выделяемые в сопротивлениях -j- на схемах замещения при прохождении токов прямой и об-

ратной последовательности в контурах ротора. Их можно получить как произведение квадрата тока прямой или обратной последовательности и соответствующего активного сопротивления разветвления схемы замещения:

P,f = 2lVf; Рэь = 211г'ь;

r/ = Re-

Гб = Ке

+ ЦХт +Xs)

1-t) 1 +tl

Подставив в формулу (2-13), получим М = iff П-Пгь).

В частном случае, когда ротор машины неподвижен {v

Tf =Гь = Ке

If-ll = ±l{l-ji){l + jf)-{i+jl){!-jl\)]=.

= (/о4-/d/q) = m (/d/q) = IdIq sin p

(где p - фазовый сдвиг между токами в обмотках D и Q), найдем выражение для пускового момента

=-Лк- sin р. (2-14)

Выражения токов (2-12), найденные методом симметричных составляющих, можно получить из уравнений ЭДС обобщенной машины в осях dug, имеющей матрицу сопротивлений Z (1-16), если paccMaTpneaTj. переход к симметричным составляющим как преобразование координат. Действительно, из выражений (2-10) находим

ioif + h /q-]( -/ь)-

Аналогичные соотношения запишем для контуров ротора. Тогда матрица преобразования токов примет вид

Для того чтобы отличать токи прямой и обратной последовательности статора и ротора, им присвоены индексы с и р . Согласно общим законам преобразования координат получим уравнения ЭДС в осях fc, be, /р, bpi

2 fee

fp bp

/с

ZD + ixm+-

Zd + JXm + - 0

/;cm(l-ft>)

h iXm

r-hix(i-

V)

ixm 0

r+ix(l+v)

Ud -JUq Ud + JUq

где Z = Zq-Zd, X= Xm+ Xs.

Разделив 1-е и 2-е уравнения на 2, а 3-е и 4-е - соответственно на 2 (1 -и) и на 2 (1 -f v), находим

be fp

Zd + JXm +

jXm 0

Zd -f /дст -f

+ ix

+ix

(2-15)

Этим уравнениям соответствует схема замещения, изображенная на рис. 2-8. Заменяя параллельные цепи ротора на рис. 2-8 эквивалентными сопротивлениями и обозначая ,

ZDf - Zd-V

- сопротивление прямой последов атель-

\Хт \\xs Л-

ности фазы D; Zob = Zo ----сопротивление обратной

l-bt-

последовательности фазы, получим более простую схему замещения асинхронной машины (рис. 2-9). Этой схеме соответствует система уравнений

fc ZDf+-

ZDb + -

Ud-JUq Ud + JUq