Полные производные по переменной времени определяются выражениями

tf/(x, U. t) df dx df du df

ж+-5ж+-аг (1-4-29)

dHx.x.t) di dx di rfu df

dt ~d~df4rlt (1-4-dU)

которые формально совпадают (первая формула получается из второй, если вектор f заменить на скаляр /). В этом смысле используемые обозначения очень удобны.

Заметим, что для функций g(x) или g(x), не зависящих явно от аргументов и и /, формулы (1.4-29) и (1.4-30) приводят к широко используемым соотношениям

dg(x) Jdx ,

dt а-т dt {1А61)

tfg(x) dg dx

Транспонируя последнее соотношение, получим

tfg(x) dx dg dt ~ dt dx

(1.4-33)

Можно также написать частные производные второго порядка, например

аг/ (X. U. Q а2/(х, ц. О дх du du dxJ

Из этих обозначений следует, что в первом случае берется частная производная вектора-строки дЦди по вектору-столбцу х, а можно найти и частную производную вектора-столбца дЦдх по вектору-строке и' . Таким образом, использованные обозначения не закрепляют порядок определения частных производных.

1.5. ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ

Обычные правила дифференцирования по скалярному аргументу легко распространить на случай произведения матричных функций. Следует иметь в виду, что результат такого диффе-

ренцирования существенно зависит от порядка сомножителей:

=v + u. (1.5-1)

- = - + А^. (1.5-2)

rf(AB) dk т dt - dt dt (i--*)

Прежде чем перейти к правилам дифференцирования по векторному аргументу, заметим, что

dx d ,

- = х^ = 1. (1.5-4)

Элементы г-го столбца якобиана, соответствующего производной

Д(Е(х))

определяются равенством, аналогичным выражению (1.4-32):

(- .....

Отсюда получим цепное правило дифференцирования сложной функции:

rft(g(x)) d\ dg dx dg dx

Этот же результат можно получить, если рассматривать производную вида (1.4-31) по векторному аргументу

dfj dfj ag dx rfg rfxT

которая соответствует /-й вектору-строке якобиана df/dx.

Разумеется, правило дифференцирования сложной функции применимо также и в случае, когда некоторые векторы f, g, х обращаются в скаляры. Применяя формулу (1.5-4), найдем производную скалярного произведения х'с = с'х и производ-

Г-XT- (1-5-5)

ную вектора Ах:

£=сТ = сТ1 = сТ, (1.5-6)

dx dx

= А- = А1 = А. (1.5-7)

Эти формулы получены умножением справа дифференциального оператора djdx на матрицу-строку при условии, что вектор-строка с' и матрица А не зависят от вектора х.

Применяя цепное правило, можно найти производную квадратичной формы Q =Q(x) = х'Ах. Пусть у = Ах, а /(х, у)= = х'у = у'х. Тогда

dQ df df dy dx dx dy rfx *

Используя формулу (1.5-6), получим

df dyx T dx- ~ У

df dxy T

dy dy

Согласно правилу дифференцирования (1.5-7),

dy dAx

aT - dx

= A.

Таким образом, - = - = ут-f xA = xW + xA = xT [AT + А]. (1.5-8)

Кроме того, если A = I, то

=-2хТ. (1.5-9)

Пользуясь правилом дифференцирования сложной функции и равенством (1.5-8), легко найти производную квадратичной формы Q (и) = (х)Ru (х):

Производная билинейной формы uT(x)Rv(x) запишется в виде

duRx dtiRv d\ . dxRu du тр d\ рт du - = -l+ 7u dx

(1.5-11)

Полагая R=I, получим

= -bv-f. (1.5-12)

dx dx dx

Умножая слева дифференциальный оператор djdx на матрицу-столбец, получим формулы дифференцирования по векторному аргументу х:

= 1, (1.5-13)

= с, (1.5-15)

T=A. (1-5-16)

=[AT-fA]x, (1.5-17)

- = 2x, (1.5-18)

J[RT + R]u, (1.5-19)

Rv-fRu. (1.5-20)

u. (1.5-21)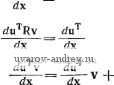

ЛИТЕРАТУРА

1. Pipes L. A. Matrices in Engineering, Electrical Engineering, 1937. 56, № 9, pp. 1177-1190.

2. Penrose A. Generalized Inverse for Matrices, Proc. Cambridge Phil. Soc, 1955. 51, pp. 406-413.

3. Frame J. S.. Koenig H. E. Matrix Functions and Applications. IEEE Spectrum. Pts II. Ill, 1964.

4. Frame J. S. Matrix Functions and Applications. IEEE Spectrum, Pts. I, IV.. V 1964.

5. Plotkin M. Matrix Theorem with Applications Related to Multivariable-Control Systems. IEEE Trans. Autom. Control, 1964, AC-9, pp. 120-121..

6. Sain M. K. On the Control Applications of a Determinant Equality Related!

to Eigenvalue Computation, IEEE Trans. Autom. Control, 1966. AC-11 pp. 10111.

7. Chen C. F.. Sien L. S. A Note on Expanding PA + AP = - Q, IEEE Trans. Autom. Control, 1968, AC-13, № 1, pp. 122-123.

8. Hoskins R. F. The Theory of Unear Continuous Systems. Intern. J. Control. 1965, 1, pp. 335-361.

9. Csaki F. Some Remarks about Recent Notations in Matrix Analvsis, Periodica Polytechnica, Electrical Engineering, 1971. 15, 156-165.

2. ПЕРЕМЕННЫЕ СОСТОЯНИЯ. УРАВНЕНИЯ СОСТОЯНИЙ

В настоящее время в технике автоматического регулирования и управления (особенно для нелинейных систем) широкое распространение получили методы пространства состояния. Эти методы возникли в связи с переходом к описанию объектов

x(t)

0> c(t)

Рис. 2-1. Блок-схема линейной нестационарной системы.

управления уравнениями состояний, заданными во временной области [35*, 135*, 145*, 151*]. Однако частотные методы продолжают играть значительную роль, особенно в задачах анализа и синтеза линейных систем. Проведем сравнительный анализ

f(x.u.f)

о

Рис. 2-2. Блок-схема нелинейной нестационарной системы.

Этих методов, начав со случая линейной стационарной системы. Предварительно запишем общие уравнения состояния нелинейных нестационарных систем (объектов управления) [1-6, 8]:

i() = f(x(0, и(0, 0. /о 14

y()=-g(x(4 u(4 t). f

Общие уравнения состояния линейных нестационарных систем

(объектов) имеют вид

x(0 = A(0x(0 + B(0u(0,

где матрицы АС), ВС), C(t), D(t) зависят от времени. На рис. 2.1 представлена блок-схема линейной нестационарной системы, а на рис. 2.2 - блок-схема нелинейной нестационарной системы.

2.1. ОПРЕДЕЛЕНИЕ ПЕРЕДАТОЧНОЙ МАТРИЦЫ ОБЪЕКТА УПРАВЛЕНИЯ, ЗАДАННОГО УРАВНЕНИЯМИ СОСТОЯНИЯ

Линейный стационарный объект управления задается уравнениями с постоянными коэффициентами

kit) = Axit) + Bn{t), y{t) = Cx{t)+Du{t),

или

X = Ах + Bu,

y = Cx + Du, -

где X = X() - вектор состояния, и = и() - входной вектор управляющих переменных, у = у ()-выходной вектор управляемых переменных. Векторы-столбцы х, и и у имеют размерности п X 1, X 1 и Х1 (в большинстве случаев q = г). Размерности постоянных матриц А, В, С и D равны соответственно пХп, пХг, qXn и дХг. Блок-схема данной системы приведена на рис. 2-1, в которой вместо переменных матриц следует рассматривать матрицы с постоянными коэффициентами.

Пользуясь преобразованием Лапласа (результат преобразования принято обозначать прописными буквами), получим

sX(s)-x(0) = AX(s)-f BU(s), (2.1-3)

Y(s) = CX(s)-f DU(s). (2.1-4)

Перепишем первое уравнение в следующем виде:

[sl-A]X(s) = BU(s)--x(0).

Его решение:

X (S) = И - А]-> В и (S) -Ь [si - А]- X (0). (2.1-5)

Подставив это выражение во второе равенство, получим

Y (S) = [С [si - А]-1В -ь DJ и (S) -Ь С [si - AJ- х (0). (2.1-6)

Так как передаточная функция (передаточная матрица) определена для нулевых начальных условий, то очевидно, что передаточная матрица между вектором входных переменных и вектором состояния имеет вид

Go(s) = [sI-A]-iB = ©(s)B, (2.1-7)

тогда как равенство

G (S) = С [si - А]- В + D = СФ (S) В + D (2.1-8)

определяет передаточную матрицу между векторами входных и выходных переменных (рис. 2.1-1). Здесь Ф(s) =[sl - А]-*. По-

ы-аГв с

СЫ-Й1В*ВС

[sI-/IJ b

люсы этих передаточных матриц совпадают с нулями определителя матрицы [si - А], т. е. с собственными значениями матрицы А. Обратная матрица [si - A]-i определяется по формуле (1.1-12). В том случае если система(объект управления) управляема и наблюдаема (эти понятия рассмотрены ниже), каждое собственное значение является полюсом; в общем случае это необязательно.

Рис. 2.1-1. Передаточная матрица Рис. /2.2-1. Блок-схема одномер-между входным вектором, вектором кого линейного объекта управле-состояния и вектором управляемых кия.

переменных.

Применяя эти формулы при r=q=\, найдем передаточные функции одномерного объекта управления.

2.2. ОПРЕДЕЛЕНИЕ УРАВНЕНИЙ СОСТОЯНИЯ

ПО ПЕРЕДАТОЧНОЙ ФУНКЦИИ (ИЛИ ПЕРЕДАТОЧНОЙ

МАТРИЦЕ)

Передаточная функция (или матрица) однозначно определяется уравнениями состояния, однако одной и той же передаточной функции могут отвечать несколько различных уравнений состояния.

Рассмотрим передаточную функцию одномерного объекта управления (рис. 2.2-1):

Y{.s)

= 0(s) =

+ CjS + Cq

j., (g-г])(5 -2) ... {.s - z)

(2.2-1)

где rn<n; К' = Ст\ U(s) - переменная управления; I( s) -управляемая переменная. Предполагается, что Рг - простые полюсы. Заметим, что передаточную функцию принято записывать в виде

Г,/\ bmS + +biS + bo

Коэффициенты в знаменателе обычно обозначаются через но, поскольку такие коэффициенты уже фигурируют в формуле (2.2-1), здесь использованы обозначения ai. Из последней формулы и выражения (2.2-1), в котором коэффициент при равен 1, видно, что ai = ai/an, Cj=bj/an. Простейший способ получения уравнений состояния состоит в разложении на элементарные дроби:

п

= (2-2-2)

Введем переменные состояния, для которых преобразования Лапласа имеют вид

Hs) = 7 U{s) (/ = 1, 2, ... , я), (2.2-3)

sXi (s) - piX, (s) = RtU(s) (/ = 1,2,..., tl). (2.2-4)

Применяя обратное преобразование (при нулевых начальных условиях), получим

xi = PiXi Л-Rill (г = 1, ... , ft). (2.2-5)

Кроме того, из соотношений (2.2-2) и (2.2-3) следует, что

Y{s)Xds) (2.2-6)

i = l

И, следовательно,

к

У = x, = XiX2 + ... -Ь х„. (2.2-7)

Отсюда, переходя к векторным обозначениям, получим

+ (2.2.8)

где

X = [х„ Х2, х„Р, А = diag[р„ р^, р„], В = /? R /? Г, С = [1, 1, 1], D=0.

Комплексно-сопряженным полюсам отвечают комплексно-сопряженные значения Ri.

U(s)

Y(s)

Рис. 2.2-2. Блок-схема объекта управления в пространстве состояний Xi(s).

Блок-схема, иллюстрирующая метод разложения с использованием преобразования Лапласа, приведена на рис. 2.2-2 (блок-схема этого метода во временной област/и приведена на рис. 2.2-3).

Ba(t) k(t)

X(t)

Рис. 2.2-3. Блок-схема многомерного объекта управления.

Для той же управляемой переменной можно определить переменные состояния также в виде

При. этом

Г(5)= RiXl{s), 1=1

(2.2-9) (2.2-10)

где по-прежнему

А = diag [а, Р2У . Рп] D = О,

В = 11, 1. 1Г и С = [Нг, .... Яп?

На рис. 2.2-4 представлена блок-схема, получаемая с учетом внесенных изменений; блок-схема на рис. 2.2-3 при переходе к переменным состояниям Xi(s) не меняется.

Для разложения на элементарные дроби выражения (2.2-1), в котором т = п, требуется прежде всего понизить степень числителя на 1 путем деления его на знаменатель. Для одномерных объектов частное представляет собой скалярную величину D = d=bnlan¥-0.

s-Pi

y(s)

Рис. 2.2-4. Блой-схема объекта управления в пространстве состояний Xi(s).

Рассмотрим теперь многомерную систему управления [47-51]. Пусть

Y(s) = G(s)U(s). (2.2-11)

Разложим на элементарные дроби передаточные функции Ojkis), образующие элементы матрицы G(s):

(2.2-12)

В этой формуле показатели Jk служат для обозначения верхних индексов. Рассмотрим случай простых полюсов.

Введем координаты состояния, для которых преобразования Лапласа имеют вид

(s) = и, (s) (/=1,2...., tij,),

Применяя обратное преобразование, получим

(2.2-13) (2.2-14)

(2.2-15) (2.2-16)