ванный метод: метод наискорейшего спуска вдали от экстремума и градиентный метод вблизи максимума или минимума.

Метод Бокса - Вилсона используется только в довольно сложных многомерных системах, когда экстремаль Q содержит значительную неопределенность. Этот метод является комбинацией метода наискорейшего спуска (подъема) и факторного анализа [18].

В факторном анализе каждая переменная Хг изменяется в окрестности рабочей точки Хо плоскости состояний с помощью пробного шага Ki по заранее составленной программе. В вычислениях используются нормализованные переменные вида

i --И

(3.4-4)

На рис. 3.4-4 показана одна из возможных программ факторного анализа для двух и трех переменных с Zi=±l.

Рис. 3.4-4. Схема факторного анализа в плоскости состояний.

Из результатов процедуры факторного анализа данные с гиперплоскости, выраженные на языке нормализованных переменных, определяются с помощью ортогонального регрессионного анализа. Например, экстремальная поверхность Q в трехмерном пространстве аппроксимируется приближенно плоскостью, заданной уравнением

Q + bXi + 22 -f йдЛз. (3.4-5)

Коэффициенты линейного полинома от многих переменных дают оценку составляющих вектора-градиента. Затем применяется метод наискорейшего спуска (подъема).

Линейная аппроксимация, безусловно, допустима только на достаточно большом расстоянии от оптимума Q. В сильно искривленной окрестности оптимума процедура факторного анализа снова повторяется для определения аппроксимирующих полиномов второго и третьего порядка. После этого нахождение точного положения оптимума становится чисто математической

задачей. Пригодность линейной модели и близость области оптимума должны быть проверены методами математической статистики [19-21].

ЛИТЕР.АТУРА

1. Казакевич В. В. Об экстремальном регулировании, в сб. Автоматическое управление и вычислительная техника , 1964, 6.

2. Draper С. S. Li Y. Т. Principles of Optimalizing Control Systems and an Application to the Internal Combustion Engine, ASME, 1951.

3. Li Y. T. Optimalizing System for Process Control, Instruments, 1952. 25,

4. OcTpoBCKHii Ю. И. Экстремальное регулирование, Автоматика и телемеханика, 1957, 18, № 9, стр. 8.52-858.

5. Хамза М. X. Синтез систем регулирования с поиском экстремума, Автоматика и телемеханика, 1964, 25, № 8, стр. 1156-1161.

6. Draper С. S., Li У. Т. Principles of Automatic Optimisation, First IFAC Congress, Moscow, 1961,

7. Казакевич В. В. О процессе экстремального регулирования инерционных объектов при наличии возмущений, Труды I Конгресса ИФАК, М., 1961.

8. Казакевич В. В. Системы экстремального регулирования и некоторые способы улучшения их качества и устойчивости, в сб. Автоматическое управление и вычыслительн я хниха , 1958.

9. Юркевич А. П. Переходные процессы в системе эстремального регулирования с динамическим чувствительным элементом. Автоматика и телемеханика, 1961, 22, № 2.

10. Фицнер Л. И. О принципах построения и методах анализа некоторых типов экстремальных систем, Доклад на Конференции по теории и применению дискретных автоматических систем, 1958.

11. Александровский И. М., Бондаревский А. С. Двухканальный автоматический оптимизатор на ферритранзисторах, в сб. Автоматическое управление и вычислительная техника , 1964, 6.

12. Фельдбаум А. А. Автоматический оптимизатор, Автоматика и телемеханика, 1958, 19, № 8, стр. 731-743.

13. Стаховский Р. И. Двухканальный автоматический оптимизатор. Автоматика и телемеханика, 1958, 19, № 8, 744-756.

14. Кутизов В. А. Тарасенко В. П. Влияние помех на работу шаговых экс-стремальных систем с переменными параметрами, Автоматика и телемеханика, 1965, 26, № 2, стр. 268-276.

15. Казакевич В. В. Об алгоритме наибыстрейшего поиска в импульсных системах экстремального регулирования. Автоматика и телемеханика, 1966,

27, № 12.

16. Перельман И. И. Один способ самонастройки шаговых поисковых систем. Автоматика и телемеханика, 1967, 28, № 4, стр. 80-93.

17. Емельянова И. М. Оптимизация процессов поиска экстремума функций с использованием априорных данных. Автоматика и телемеханика, 1967,

28, № 5, стр. 160-165.

18. Box О. Е. Р., Wilson К. В. On the Experimental Attainment of Optimum Conditions, J. of the Royal Statistical Soc, 1951. 13, Ser. B, № 1, p. 1,

19. Cochram W. O., Cox O. M. Experimental Designs, Wiley. N. Y., 1957, p. 454.

20. Налимов В. В., Чернова Н. А. Статистические методы планирования экстремальных экспериментов, изд-во Наука , 1965.

21. The Design and Analysis of Industrial Experiments, ed. O. L. Davies, 2nd ed., Imperial Chemical Industries. Ltd. Oliver and Boyd, London, 1960, p. 636.

22. Meyer-Brotz G., Herschel R. Zur statistischen Theorie Automatischer Optimlsatoren, Elektronische Rechenanlagen, 1963, 5, № 3, pp. 121-125.

23. Brammcr K. Ein selbstoptimierender Folgeregelkreis mit verstimmtera Mo-dell, Regelungstechnik, 1963. 11, № 7, pp. 306-311.

24. Bergholz O. Zur Berechnung und Modellierung selbsteinstellender Systeme mit Optimalwertsuche, Messen, Steuern, Regeln, 1964, 7, № 3, pp. 139-143.

25. Helein J.. Perret P., Rouxel R. Methode Dynamique doptimalisation, Automatisme, 1964, 9, № 3. pp. 81-88; Pt. II, № 4, pp. 145-151.

26. Burmeister H. L. Einfache und komplizierte stationare Schweingungen in Extremalsystemen. Messen, Steuern, Regeln. 1966, 9, № 8. pp. 258-268.

27. Haniza M. H. Extremum Control of Continuous Systems, IEEE Trans. Autom. Control, 1966, AC-Il, № 2, pp. 182-189.

28. Petereit P. Analyse der stationare Pendelschwingungen eines Diskontinui-erlichen Extremalsystems, Messen, Steuern, Regeln, 1966, 9, № 8, pp. 269-274.

29. Salaraon M. Statische Optimierung. Messen, Steuern, Regeln, 1966 9, № 8. pp. 255-258.

30. Ivakhnenko A. O. Desing of an Extremum .Controller that does not Hunt, Control, 1967, 11, № 2, pp. 71-74.

31. Keller D. Extremalsystem mit kontinuierlicher Arbeitsweise und abhangigem Suchprozess, Messen, Steuern, Regeln, 1967, 10, № 5, pp. 167-170.

32. Ufer W. Beschreibung eines diskontuierlich arbeitenden Extremalsystems mit abhangiger Stelleinwirkung, Messen, Steuern, Regeln. 1967, 10, № 5, pp. 171-174.

33. Levy N. M. A Hill-climbing Servo-Mechanism. Control. 1968. pp. 770-775.

34. James D. J. O. Stability and Subharmonics in a Sinusoidal Perturbation Hillclimbing System, Int. J. Control, 1971, 13, pp. 165-178.

4. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ АДАПТАЦИИ, ОБУЧЕНИЯ И ОПТИМИЗАЦИИ

Используя методы математического программирования и стохастической аппроксимации, Цыпкин [I-6, 146*] развил алгоритмы для решения задач, связанных с адаптацией, обучением, распознаванием образов, идентификацией и некоторых других подобных задач. Рассмотрим основные принципы этих алгоритмов и некоторые их приложения.

Достоинство методики Цыпкина состоит в том, что она выявляет взаимные связи и аналогии между группами задач, ранее рассматривавшимися отдельно.

4.1. КРИТЕРИЙ ОПТИМАЛЬНОСТИ

Задача оптимизации сводится в теории управления к определению экстремумов различных функционалов качества. С помощью вариационного исчисления задача упрощается до нахождения экстремумов некоторых функций. В общем случае функционал качества задается математическим ожиданием по X от функции Q (х, с):

/(c) = Mk{Q(x, с)1, (4.1-1)

где nX 1-мерный вектор х является случайным процессом с плотностью вероятностей р{х), а и-мерный вектор с представляет собой параметры или возможные внешние воздействия. Векторы X и с могут быть связаны некоторыми соотношениями и условиями, например такими, как

h(c) = MK{g(x, с)}. (4.1-2)

Это условие отражает ограничения на среднюю энергию, топливо или другие величины. В выражении (4.1-2) оба вектора-столбца h и g имеют по т составляющих {т<п). В детерминированном случае Q(x, с) можно заменить на Q(c), а g(x, с) на g(c). Плотность р{х) можно считать дельта-функцией б(х). В стохастических задачах р{х) может быть произвольной, но обычно считается заранее известной. В неадаптивных задачах предполагается только, что р{х) существует, но она не считается заранее известной.

В адаптивных задачах функционал качества /(с) и часто вид ограничений h(c) неизвестны; известными считаются только Q(x, с) и g(x, с).

Ряд критериев качества можно привести к форме (4.1-1). Например, функционал

/(c) = P{Q(x, с)<} (4.1-3)

равен вероятности того, что Q не превышает границы А > О (здесь Р-вероятность того, что условие в скобках выполняется). Вводя случайную переменную

{ 1, если Q (х, с) > k,

-{свели Q(x,c)<*, < -)

функционал /(с) можно записать в виде

/(с) = Мх{б(х, с)), (4.1-5)

что формально совпадает с выражением (4.1-1).

4.2. ПРОЦЕСС АДАПТАЦИИ И ЕГО АЛГОРИТМ

Адаптация означает изменение параметров, структуры системы или, возможно, управляющего действия на основе информации, получаемой в процессе управления, для того, чтобы перевести систему в оптимальное состояние. При этом внешние условия могут изменяться. Самое примечательное свойство адаптации состоит в непрерывном получении информации и использовании его для улучшения рабочих условий или критерия качества. Поэтому процесс адаптации можно рассматривать как последовательную аппроксимацию или итерацию [7, 8].

Рассмотрим сначала итеративные детерминированные методы. Допустим, что / (с) имеет единственный экстремум при оптимальном значении с=с . Если функция Q(x, с) дифференцируема по с, необходимое условие экстремума при отсутствии ограничений имеет вид

= М.{} = 0. (4.2-1)

В большинстве случаев уравнение (4.2-1) не имеет решения в аналитической форме. Решение c=cf можно получить итеративным процессом или поисковым методом оптимизации, например градиентным методом. Алгоритм для нахождения оптимального вектора с задается рекуррентной формулой

c{k) = c{k-\) + R{k)VJ{c{k - D), (4.2-2)

тес =d/dc или д/дс - дифференциальный оператор набла. Компоненты г (к) диагональной матрицы R() могут зависеть от числа шагов и от величины c(k-1). Если выполняются соответствующие условия сходимости итеративного процесса, то с--с при возрастании k.

Обычный градиентный метод можно использовать только тогда, когда /(с) известно. В адаптивных же процессах /(с) заранее неизвестно. В этих случаях используется алгоритм, являющийся обобщением выражения (2.4-2):

с (А;) = с (А; - 1) -f R (А;) Ve Q (X (k), c(k-l)). (4.2-3)

Уравнение (4.2-3) представляет собой стохастическую аппроксимацию [9-17]. Так как Vc Q(x, с) зависит от случайно изменяющегося состояния X, величина с (/г) также может изменяться случайно. Если выполняются некоторые условия сходимости [9-11], то c(k)c вероятностью 1 при k-oo.

Алгоритмы (4.2-2) и (4.2-3) удобно использовать для оптимизации с помощью цифровых вычислительных машин. При использовании аналоговой вычислительной машины алгоритмы должны иметь такую форму, чтобы моделировать соответствую-ime дифференциальные, а не разностные уравнения, а именно дифференциальное уравнение

-т^ (4.2-4)

вместо уравнения (4.2-2) и дифференциальное уравнение в частных производных

-птЩЦг^ (4.2-5)

вместо уравнения (4.2-3). На рис. 4.2-1 и 4.2-2 показаны блок-схемы для случая многих переменных для разностного и диффе-

7Т

F=>

Рис. 4.2-1. Блок-схема детерминированного итеративного процесса.

ренциального уравнений. Эти системы содержат нелинейный преобразователь, используемый для получения Vc / или Vc Q,

Рис. 4.2-2. Блок-схема стохастического итеративного процесса.

усилитель А с переменным коэффициентом усиления и интегратор непрерывного или дискретного типа. Каждый элемент мно гомерный.

4.3. АДАПТАЦИЯ ПРИ НАЛИЧИИ ОГРАНИЧЕНИЙ

Добавление ограничений приводит к усложнению алгоритма адаптации. При ограничениях типа уравнения (4.1-2) используется метод множителей Лагранжа:

z{k) = c{k-\) + R{k) 1 VeQ(X{k), с{к-\))Л-

+ Q{x{k), c{k-\))-k{k-\%

X (A;) = X (A; - 1) -f P (A;) g (x {k), c{k~-\)),

где Х-таХ 1-мерный вектор-столбец.

(4.3-1)

(4.3-2)

является пХпг-матрицей и, наконец, R и Р - соответственно пХп и тХт диагональные матрицы. Блок-схема итеративного процесса приведена на рис. 4.3-1.

Алгоритм можно также распространить на случай ограничений в форме неравенств.

Вышеописанный алгоритм является одношаговым, а не поисковым. Однако часто бывает, что градиент заранее определить

Р

к

7Г

7>

,4 R

с

Рис, 4.3-1. Алгоритм адаптации при наличии ограничен.ч.ч.

нельзя и для его нахождения требуется дополнительный, многошаговый поисковый алгоритм, аналогичный алгоритмам, используемым в оптимальных системах, описанных выше.

4.4. РАСПОЗНАВАНИЕ ОБРАЗОВ

Основной принцип распознавания образов состоит в том, чтобы построить поверхности, разделяющие гиперпространство на конечное число областей, каждая из которых имеет свой образ. После процесса обучения распознавание означает, что известные типы будут правильно приписываться одному из классов, определенных таким образом, а если появляется неизвестный тип, не имеющий отношения ни к одному известному классу, то ему приписывается новое подразделение гиперповерхности.

Хотя задача распознавания образов возникла в связи с хорошо определенными конфигурациями, такими, как цифры, буквы, звуки, симптомы и т. д., сфера ее приложения значительно более общая. Распознавание образов является первой стадией обработки информации, приходящей с чувствительных элементов и измерительных приборов.

Главная задача распознавания образов состоит в том, чтобы приписать изучаемую конфигурацию некоторому классу. Любой индивидуальный класс характеризуется конфигурациями, приписанными ему. Эти конфигурации должны обладать некоторыми общими свойствами (например, латинская буква обычного

письма будет обладать некоторыми основными свойствами, не зависящими от почерка).

Предположим, что рассматриваемые конфигурации можно характеризовать или различать с помощью заданного (большого) числа свойств. Каждой характеристике приписывается ось в пространстве состояний. Наличие свойства обозначается, например, единицей, а отсутствие-нулем. Таким образом, каждой конфигурации можно приписать подпространство пространства состояний.

Геометрически распознавание образов заключается в определении поверхностей, которые производят наилучшее разбиение (понятие наилучшее полностью определяется некоторым заранее установленным критерием) многомерного гиперпространства на подпространства, соответствующие различным классам. Гиперповерхности, производящие разбиение, устанавливаются в процессе обучения. Распознавание образов после обучения состоит в основном в проверке новых типов, о принадлежности которых к определенному классу ничего неизвестно. Вычислительная машина, осуществляющая распознавание образов, будет указывать то подпространство гиперпространства, к которому принадлежит рассматриваемый тип.

Рассмотрим функцию разбиения y=f(x), где вектор х характеризует свойства анализируемой конфигурации, а у определяет класс, в котором она содержится. Например,

у = 1, если X е Л, и у = - 1, если х^В.

Для решения этой задачи составляется аппроксимирующая функция

7(х) = сТф(х). (4.4-1)

Это конечная сумма функций фДх), г = 1, 2, п, которые линейно независимы и служат для аппроксимации /(х). Ошибка аппроксимации оценивается с помощью функционала

/(с) = Мх{/(сТф(х)-);)}, (4.4-2)

где / - строго выпуклая функция. Для вектора с, дающего наилучшее приближение, /(с) достигает минимума. Градиент равен

VeQ (X, с) = F (с> (X) - у) ф (X), (4.4-3)

где -производная от F по ее аргументу. Подставляя уравнение (4.4-3) в уравнение (4.2-3), получим

c{k)c{k-l) + R{k)Flc{k-\)4>(X (k)) - у ik)\ ф(X (k)).

(4.4-4)

Аналогично для непрерывного алгоритма обучения распознаванию образов имеем

Ч- R (О F [с^ (О Ф (X (/)) - у (/)] ф (X (0). (4.4-5)

Таким образом, два последних алгоритма можно представить нелинейными нестационарными разностными или дифференциальными уравнениями. На рис. 4.4-1 приведена блок-схема, соответствующая уравнению (4.4-4). Это по существу блок-схема персептрона. Она отличается от блок-схемы, впервые предложенной Розенблатом [124*], тем, что в ней вместо специальных пороговых функцийф(х) можно брать функцииф (х), состоящие из произвольных линейно независимых составляющих. Персеп-троны, содержащие пороговые элементы, обычно рассматри-

функциональный генератор

Скалярное произведение Задержка

Фуннцио-мамьный генератор

Рис. 4.4-1. Блок-схема персептрона.

ваются как технические аналоги нервной системы живых организмов. Действительно, имеются некоторые аналогии между этими системами распознавания образов, т. е. между нервной системой живого организма и конечным автоматом. Еще более простая блок-схема персептронной модели нервной системыбыла предложена Видровым [23], который допускает в качестве единственных возможных ситуаций только поверхности гиперкубов.

Кроме того, можно построить еще более общий алгоритм распознавания образов, если принять во внимание, что знаки точной и аппроксимирующей функций разделения должны совпадать.

Задачу распознавания образов можно свести к решению совместной системы линейных неравенств [19-26]. При этом должен быть найден вектор с, для которого знаки функций y=f(x) и f(x) одинаковы, т. е. этот вектор удовлетворяет неравенству у(;)сТ(-1)ф(х(А;))>0. (4.4-6)

Это неравенство можно свести к уравнению, записав его в виде

у{к)с^{к-1)ц> (X (к)) = й (А; - 1). (4.4-7)

Вектор с , удовлетворяющий этому уравнению, можно опре делить, минимизируя функционал

/(с, а) = М. {F(y с^ф(X) -а)}, а>0. (4.4-8)

Для решения задачи распознавания образов можно использовать теперь следующий алгоритм:

c{k) = cik-l) + Rik)F [у ik)ст(А; 1)X

X Ф(х (k)) - й (А; - 1)] у (А;) ф (X (k)), (4.4-9)

aik)a{k-\)-P(k){F[y{k)c{k-\)if{x{k))-a{k-\)] + + \F\y (k)ст(A; - 1)ф(X{k}) -a{k-\)]\]. (4.4-10)

Блок-схема алгоритма, задаваемого уравнениями (4.4-9) и (4.4-10), приведена на рис. 4.4-2. Она отличается от блок-схемы

Функциональный генератор

чое

Скалярнс произведение Задержка

у(к)<р(х.(к)) у(к)с\к-1Шк))

a(k-f)

cik-t)

<4F

Функциональный генератор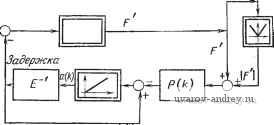

Рис. 4.4-2. Блок-схема алгоритма распознавания образов.

классического персептрона, показанной на рис. 4.4-1. Подобная структурная модификация персептрона позволяет ускорить процесс распознавания образов.

4.5. ИДЕНТИФИКАЦИЯ

При проектировании автомашческих систем управления одним из важнейших этапов является идентификация [27-32, 126*] (ее обычно характеризуют как определение статических и