п

Палаш

-1.50000 . J .86603

-1.83891 . J 1.75438 -2.32219

-2.1037Э -2.89621

-2.32467 -3.35196 -3.6467+

-2.51593 -3.73S71 -4.24636

-2.68568 -4.07014 -4.75829 -4.97179

J 2.65742 J .86723

J 3.57102 J 1.74266

J 4.49267 J 2.62627 J .86751

J 5.42069 J 3.51717 J 1.73929

-2.63898 ♦ J 6.35391

-4.36829 . J 4.41444

-5.20484 . J 2.61618

-5.58789 ♦ J .86761

-2.97926

-4.63844

-5.60442

-6.12937-

-6.29702

-3.10892 -4.88622 -5.96753 -6.92204 -6.61529

J 7.29l4 J 5.31727 J 3.49616 J 1.73785

J 6.23270 J 6.22499 J 4.38495 J .86767 J 2.61157

3.00000 6.45943

11.48780 9.14013

18.15632 14.27248

26.51403 20.85282 18.80113

36.59679 28.936S5 25.66644

48.43202 38.56925 33.93474 31.97723

62.04144 49.76850 43.64665 40.56927

77.44270 62.62559 54.83916 48.66755 50.58236

Э.00000 3.67761

4.20758 5.79242

4.64935 6.70391

5.03186 7.47142 8.49672

5.3713S 6.14028 9.51658

5.67797 e.73658 10.40968 11.17577

S.95852 - 9.27688 11.20664 12.25874

6.21783 9.77244 11.93506 13.64409 13.23058

Процентах (как показано на рис. 2.5-2) и амплитуды в децибелах (как показано на рис. 2.5-3) [8]. Оба эти показателя суть функции величины соТ, где Т - идеальное ГВП, которое и откладывается по оси абсцисс. Так как произведение соГ безразлично, оно не оказывает влияния на нормирование частоты. При применении указанных оценок для определения требуемого порядка фильтра, следует иметь в виду, что если должны удовлетворяться одновременно требования по точности и ГВП и амплитуды, то надо использовать ту оценку, которая дает более высокий порядок фильтра. Значения номиналов элементов цепи при реализации фильтров Томсона различного порядка резистивно нагруженными лестничными цепями без потерь можно найти в приложении А.

Положение полюсов и коэффициенты квадратичных множителей (ao+ais+s) линейно-фазовой (томсоновской) функции цепи нижних частот с нормированным ГВП (при постоянном токе) 1 с

. На основе функций, определенных выше, можно получить другой набор функций цепи, имеющих линейную ФЧХ. Чтобы убедиться в этом, заметим, что функция цепи, имеющая вид

Nis)-=H/[m{s) + n{s)], (24)

где m(s)-четная часть полинома в знаменателе, n{s)-его нечетная часть, имеет следующую ФЧХ:

arg N{}io)- arctg [п (j (u)/j m (j со)], (25)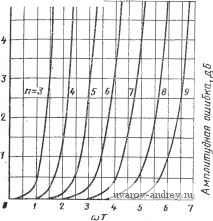

Рис, 2,5-2. Ошибки группового времени прохождения, полученные при использовании линейно-фазовых фун-кций, приведенных в табл. 2.5-1

О 0,5 1,0 f,5 2,0 2,5 3,0 3,5 4

Рис. 2.5-3. Ошибка воспроизведения амплитудно-частотной функции, полученная при использовании линейно-фазовых функций, приведенных в табл. 2.5-1

Рассмотрим теперь, что произойдет, если сформировать функ* цию цепи в виде

Nbn (S) H[m{s)-n Шт (s)+ (s)]. (26)

Легко показать, что для такой функции

Л^(](о)

Н, т. е. амплитуда постоянна для всех частот. Эта функция называется всепропуекающей функцией цепи. Фазочастотную характеристику такой функции легко найти:

argiVBn(Ju)=-2arctg[n(j(u)/jm(i(o)]. (27)

Таким образом, форма ФЧХ всепропускающей функции идентична форме исходной функции, если не учитывать масштабного множителя 2.

Определение идеальной передачи, приведенное выше, можно расширить, если рассмотреть, что произойдет при подаче импуль-Са на вход произвольной цепи, характеризуемой функцией цепи A(jcu). Такой вид воздействия удобен тем, что его максимальное значение можно распознать в форме выходного сигнала.

Реакцию на импульсное воздействие или импульсную переходную характеристику h{t) можно найти, если воспользоваться обратным преобразованием Фурье:

/г (О = - In (j ©) е^ dco = -ТI Л/ (j со) cos [со t + argN (j to)] da. (28)

В этом выражении интеграл будет иметь наибольшее значение, когда аргумент косинуса под знаком интеграла будет постоянным. Таким образом, максимальное значение h{t) достигается, когда

-[©-farg/V(jto)]=0. (29)

Решая это уравнение, можно определить функцию времени прохождения 0{а))* произвольной цепи в виде

D(to)=---argiV(j©). (30)

Очевидно, что в рассмотренном выше случае идеальной передачи, когда argiV(j(u)=-соо, получим, что D(.m)=o, а для всех частотных составляющих входного сигнала ГВП, равно in секунд. Из приведенного выше следует, что максимально линейная (в начале координат) ФЧХ фильтров Томсона обеспечивает (в начале координат) максимально плоскую характеристику времени прохождения. Таким образом, этот фильтр называют также фильтром максимально плоского группового времени прохождения (МПГВП-фильтр).

2.6. Характеристики во временной области

В предыдущих параграфах этой главы были рассмотрены некоторые свойства функций цепи в частотной области. В этом параграфе кратко рассмотрим некоторые из основных свойств этих функций во временной области. В отличие от частотной области, где можно было получить общие окончательные соотношения, связывающие реакцию и воздействие, во временной области реакция должна быть определена отдельно для каждого вида воздействия. Ради простоты представления ограничимся лишь случаем, имеющим наибольший практический интерес, а именно, реакцией ФНЧ на ступенчатое воздействие. Этот случай особенно важен при изучении импульсных и цифровых систем передачи данных.

Единичное ступенчатое воздействие e{t), прикладываемое в момент =0, можно записать в виде

e{t) = u{t)\2 < (1)

* Ее называют также функцией группового времени прохождения (ГВП).

где и (О-единичная ступенчатая функция, показанная на рис. 2.6-1. Реакция фильтрации на такое воздействие r{t) называется ступенчатой реакцией или переходной характеристикой. Для идеальной функции цепи эта характеристика определяется выражением (12) в § 2.5, которое теперь примет вид

= 0, t<to;

r{t) = u{t-t,)

= 1. t>t.

Характеристика приведена на рис. 2.6-2. Фактически для неидеальной функции цепи нижних частот переходная характерис-

Рис. 2.6-1. Единичное ступенчатое воздейстаие

О to t [sj

Рис. 2.6-2. Идеальная реакция на единичное ступенчатое воздействие

тика обычно имеет форму, более похожую на ту, что изображена на рис. 2.6-3; из рисунка видно наличие колебательного процесса, отмеченного на вершине ступеньки характерным выбросом (перерегулированием). Он называется процессом затухания колебаний. По кривой на рис. 2.6-3 можно определить некоторые об-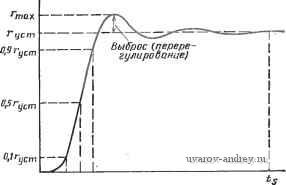

t(s)

Рис. 2.6-3. Фактическая реакция на единичное ступенчатое воздействие (переходный процесс)

Щеизвестные критерии качества, используемые для оценки переходной характеристики, такие, например, как время запаздывания d, определяемое как время, требуемое для достижения реакций Уровня, соответствующего 50% от окончательного установившегося значения Густ; Ао%-время, необходимое для достижения

уровня, соответствующего 10% от установившегося значения; 90 % - время, необходимое для достижения уровня, соответствующего 90% от установившегося значения. Используя две последние оценки, можно определить время нарастания

tr = fco%-10%. (3)

Другие интересные параметры переходной характеристики следующие: ts - время установления (переходного процесса), означающее время, необходимое для того, чтобы, затухая, остаточные колебания на вершине характеристики уменьшились до определенной величины, обычно ±2% от установившегося значения; перерегулирование, которое обычно определяется максимальной относительной величиной выброса (MOB), заданной в процентах:

MOB = [(- уст)/-уст] ЮОо/о. (4)

В общем случае .можно сказать, что хорошие характеристики во временной области соответствуют малым значениям U, U и и MOB.

Некоторые параметры переходной характеристики, определенные выше, можно с некоторым приближением сопоставить с параметрами в частотной области, определенными в § 1.3. Напри мер, для функции цепи нижних частот, у которой величина выброса мала (меньше 5%), время нарастания U и ширина полосы пропускания на уровне -3 дБ сос связаны приближенным соотношением

,С0с 2,2. (5)

Для иллюстрации этого соотношения рассмотрим схему цепи на рис. 2.6-4. Ее передаточная функция по напряжению

12 (S)/11(S) = 1/(5+1)- (6)

Легко показать, что частота среза для нее равна 1 рад/с. Переходную характеристику можно определить как

f2(0 = (l-e-0 (0- (7)

Из этого соотношения находим, что о / =0,1054s, а Uo%= =2,3026 S. Следовательно, r=2,1972s, а гСОс равно также 2,1972, что хорошо согласуется с приближенным значением 2,2, предсказанным в (5).

Некоторые примеры переходных процессов для различных порядков фильтров Баттерворта и Чебышева (амплитуда пульсаций 1 дБ), рассмотренных ранее в этой главе, показаны на рис. 2.6-5 и 2.6-6. Из этих характеристик можно видеть другую общую черту, связывающую временную и частотную области: выброс и время установления переходного процесса возрастают с увеличением крутизны среза АЧХ. В результате этого функции фильтрации более высокого порядка имеют более значительный

затухающий колебательный процесс, чем функции более низкого порядка, причем у чебышев'ских функций он проявляется сильнее, чем у баттервортовских. Другое интересное свойство этих функций состоит в том, что (для постоянного выбранного значения нормированной ширины полосы) их время запаздывания возрастает с возрастанием порядка, тогда как время нарастания почти постоянно.

1ф Vz

Рис. 2.6-4. Пример цепи. Значения элементов даны IB омах, фарадах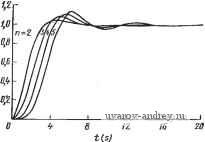

Рис. 2.6-5. Переходный процесс (ступенчатая реакция) для функций Баттерворта

Свойства функций Бесселя (или фильтров Томсона), рассмотренных в § 2.5, существенно отличаются. Переходные процессы для них показаны на рис. 2.6-7, откуда можно видеть поразительный результат, определяемый линейно-фазовыми свойствами этих функций и выбранной для них нормированной постоянной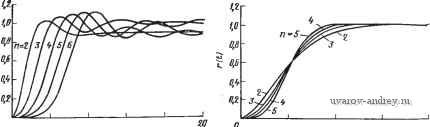

S 12

t(s) Переходный

.1.0

Pw. 2.6-6. Переходный процесс (ступенчатая реакция) для функций Чебышева (амплитуда пульсаций 1 дБ)

2.0 i(SJ

Рис. 2.6-7. Переходный процесс (ступенчатая реакция) для функций Томсона

Времени прохождения. Прежде всего, это отсутствие выброса. Кроме того, время нарастания уменьшается с увеличением порядка фильтра. Очевидно, что функции Бесселя имеют значительно лучшие временные характеристики, чем функции Баттерворта, которые, в свою очередь, в этом отношении лучше, чем функции Чебышева.

2.7 Выводы

В этой главе были рассмотрены несколько основных тем из области аппроксимации. Первые три темы были связаны с мето- дами аппроксимации АЧХ ФНЧ. Так, в § 2.1 обсуждались максимально плоские- или баттервортовские, АЧХ. Характерным здесь было то, что фактически аппроксимация проводилась для одной частоты ((й = 0). Затем в § 2.2 была описана равноволновая или чебышевская АЧХ; аппроксимация в этом случае проводилась для всей полосы пропускания в целом. Наконец, в § 2.3 была описана эллиптическая, или кауэровская, АЧХ; аппроксимация при этом проводилась как в полосе пропускания, так и в полосе задерживания. Из этих трех видов аппроксимации для заданного порядка фильтра эллиптические характеристики обеспечивают наиболее крутой срез на границе полосы пропускания и полосы задерживания, затем в порядке уменьшения крутизны среза следуют чебышевские и баттервортовские характеристики. С другой стороны, из этих трех аппроксимаций, как было показано в § 2.6, баттервортовская аппроксимация обеспечивает лучшую форму переходного процесса, затем, в порядке ухудшения, следуют чебышевская и эллиптическая аппроксимации. Хотя все эти аппроксимации первоначально определялись для функций цепи нижних частот, их можно было легко преобразовать для функции цепи верхних частот и полосовых функций, используя методы, изложенные в § 2.4. Томсоновская (или бесселева) линейно-фазовая аппроксимация (максимально плоская характеристика группового времени прохождения) обеспечила значительно лучшую форму переходного процесса по сравнению с тем, что давала баттервортовская функция. Это показано в § 2.5.

Работ, посвященных теории аппроксимации, очень много, они отражают широкий круг исследовательских интересов многих спе циалистов на протяжении ряда лет. Методы и техника, описанные в этой главе, отбирались так, чтобы осветить наиболее полезные и широко известные результаты, полученные в этой области. Ограниченный объем книги не позволил рассмотреть многие другие интересные, но не так широко используемые методы аппроксимации, такие как обратная чебышевская, гауссовская и некоторые промежуточные типы аппроксимации. Их изложение, однако, можно найти в списке рекомендованной литературы.

2-1 (§ 2.1). Для приведенных ниже функций цепи Ni(s) найдпте амплитудно-частотную функцию i\/i(j(o)2 и покажите, что она равна отношению четных полиномов

а) Na{s)H/(s + as+b);

б) Nb{s)== H(s + c)/(s+as+b);

в) \/c(s) = Я/(sЗ+2s2-2s-l).

2-2 (§ 2.1). Покажите, что приведенным ниже ф'ункцням цепи iVi(s) соответствуют коэффициенты передачи, не зависящие от частоты. Подобные фунщии называются всепропускающими.

a)Na{s) = H(,s-a)Hs+a); б) Nt (s) = Н (~as + b)/{s + as+b). 2-3 (§ 2.1). Найдите N{s), если она существует, для следующих функций:

а) i\/(jm)2=(l-со2)/(а.* -4m2-f8) ; б) ]N (] m) 12 == (1 + co2)/m (m* + 1); в) Л/аа))Р = ((в*-2 0)2+l)/(l-f ©2) (о,4 Зц,2/2+25/16).

2-4 (§ 2.1). Для следующей ниже функции цепи N(s) определите значение постоянной а, при котором Л^(] сй) соответствует максимально плоской АЧХ N(s) = {s+l)f(s4as+l).

2-5 (§ 2.1). а) Покажите, что постоянная е в (iI2) (см. § 2.1) может рассматриваться как постоянная частотного нормирования и определите соответствующее ей выражение для частотного нормирования.

б) Используя данные примера 2.1-3, найдите частоту, при которой значение i\/(jfi> в (12) (для 8=1 и п=5) уменьшается на 0,5 дБ, и убедитесь затем, что при удвоении указанной частоты знаменатель (12) имеет то же значение, что и выражение (iI9) (при п=5).

2-6 (§ 2.1). а) Определите передаточ1Ную функцию для ФНЧ, имеющегэ максимально плоскую АЧХ с затуханием 1 дБ на частоте 2 рад/1с и 30 дБ на частоте 6 рад/с. Используя (12) в § 2.1, определите порядок аппроксимирующей функции, а используя (15), найдите положение полюсов.

б) Удостовертесь в правильности результатов, полученных в п. а), используя рис. 2.1-4 и табл. 2.1-13.

в) Полагая, что желаемая функция представляет собой передаточную полную проводимость и используя приложение А, найдите реэистивно нагруженную (iR=l) лестничную реализацию без потерь.

2-7 (§ 2.1). а) Найдите функцию цепи нижних частот с максимально плоской АЧХ, имеющую затухание 3 дБ на частоте 1 кГц и 20 дБ на частотах выше, чем 2,5 кГц.

б) Используя приложение А, найдите реализацию этой функции в виде лестничной цепи без потерь, нагруженной резистором с сопротивлением 1 кОм.

2-8 (§ 2.2). Определите полином Чебышева С7(о)), используя соотношение, приведенное ,в (2), § 2.2.

2-9 (§ 2.2). Докажите, что велнданы е, п а v связаны соотношением

e =(Vl/e2+l + l/e)i/n.

2-10 (§ 2.2). а) Определите передаточную функцию ФНЧ, имеющего равноволновую характеристику с амплитудой пульсаций 1 дБ в полосе пропускания шириной О ... 2 рад/с я затухание не менее 30 дБ на частоте 4 рад/с. Используйте выражения (1) и (3) из § 2.2 для определения порядка аппроксимирующей функции и выражение (12) для нахождения положения полюсов.

б) Подтвердите правильность результатов, полученных в п. а), используя рис. 2.2-5 и табл. 2.2-2.

в) Полагая, что желаемой .функцией является передаточная полная проводимость, и используя приложение А, найдите резистивно нагруженную {R=l) лестничную реализацию без потерь.

2-11 (§ 2.2). Определите минимально необходимый порядок п для равноволновой функции с АЧХ, имеющей амплитуду пульсаций 0,5 дБ в полосе пропускания О ... I рад/с и затухание 3,01 дБ на частоте не выше 1,1 рад/с.

2-12 (§ 2-2). Найдите положение полюсов и .нулей функции цепи второго порядка, имеющей равноволновой характер с амплитудой пульсаций в пределах О ... 0,29289 в полосе задерживания шириной 1 рад/с ... оо и монотонный характер в полосе пропускания шириной О ... I рад/с.

2-13 (§ 2-3). а) Найдите требуемый порядок функции цепи с максимально .плоской АЧХ, затухающей на 1 дБ при частоте I рад/с и на 38 дБ при частоте 1,5 рад/с.

б) Выполните то же задание, НО для равноволновой функции.

в) Выполните то же задание, но для эллиптической функции.

г) Если исключить четный порядок (случай А) эллиптической функции, какой порядок эллиптической функции потребуется?

2-14 (§ 2.3). а) Найдите эллиптическую функцию цепи нижних частот, имеющую амплитуду пульсаций 1 дБ в полосе пропускания О ... 1 рад/с и затухание не менее 50 дБ для всех частот выше 2 рад/с.

б) Для такой функции цепи определите величину мультипликативной постоянной такой, чтобы максимальное значение амплитуды было равно единице.

2-15 (§ 2.3). Найдите лестничную без потерь реализацию цепи для эллиптической передаточной (по напряжению) функции цепи нижних частот, имеющей амплитуду пульсаций 1 дБ ,в полосе пропускания О ... 1 кГц и затухание не менее 34 дБ .Ha всех частотах выше 2 .кГц. Фильтр должен иметь двустороннюю (на входе и выходе) резистивную нагрузку 1 кОм.

2-16 (§ 2.4). а) Используя узкополосную аппроксимацию, найдите положение ПОЛЮСОВ для полосовой функции цепи, имеющей равноволновую характеристику шестого порядка с допуском в полосе иропускания 1 дБ. Примите ширину полосы, равной 0,1 рад/с, и среднюю частоты - 1 рад/с.

б) Сравните .полученные результаты с теми, что приведены в табл. 2.4-5.

f/y/z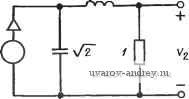

Рис. 32-17. Значения элементов даны в омах, генри, фарадах

2-17 (§ 2.4). Цепь, схема которой показана иа рис. 3.2-17, имеет максимально плоскую АЧХ ФНЧ с частотой среза на уровне -3 дБ, равной 1 рад/с. Желательно применить к этой цепи соответствующее преобразование частоты, чтобы получить режекторную цепь со средней (геометр.ически) частотой 1 рад/с и шириной полосы 1/3 рад'с.

Указание. Постарайтесь использовать следующие процедуры.

а) Сначала преобразуйте заданную цепь в цепь верхних частот (с частотой среза 1 рад/с на уровне - 3 дБ), затем примените ФНЧ-ПФ-преобразова-ние к нормированной по частоте цепи верхних частот;

б) Сначала нормируйте по частоте заданную цепь нижних частот, затем примените ФНЧ-ПФ-преобразовэние, а после этого ФНЧ-ФИЧ-преобразо-вавие. Если результирующие цепи получатся неодинаковыми, объясните причину расхождений.

2-18 (§ 2.4). а) Используйте ФНЧ-ПФ-преобразование для нахождетш фуинции цепи РФ четвертого порядка с максимально плоской АЧХ, со средней частотой 1 рад/с и шириной полосы 1 рад/с, ограниченной частотами, соответствующими затуханию 3 дБ по отношению к уровню передачи на частотах, равных О и оо в полосе пропускания. Выразите результат в виде отношения полиномов.

б) Решите приведенную выше задачу, нопользуя уэкополосную аппроксимацию, сравните полученные результаты.

2-19 (§ 2.4). Реясекторная цепь, схема которой дана на рис. 3.2-19 имеет максимально плоскую АЧХ в полосе пропускания. Средняя частота

3 v/r

Рис. 32-J9. Значения элементов даны в омах, генри, фарадах

полосы задерживания равна 1 рад/с и ширина полосы (на уровне - 3 дБ от максимального значения в полосе пропускания) УЪ рад/с. Найдите соответствующее преобразование частоты, необходимое, чтобы преобразовать ее в цепь нижних частот второго порядка с максимально плоской характеристикой и шириной полосы 1 рад/с.

2-20 (§ 2.4). Найдите функцию цепи четвертого порядка, имеющую амплитуду, изменяющуюси не более, чем на 1 дБ, в полосе пропускания 0,618 ... ... 1,618 рад/с, И имеющую нули (передачи) на частотах 0,3269 и 3,059 рад/с.

2-21 (§ 2.5). Определите, является ли выражение

А (т) = tg [arg Т (j m)] = (со - 2 m-2 m)/(-2 ев-+ 2) ФЧХ для какой-либо из функций цепи, приведенньЬс ниже:

а) 7<,(s)= (s-b l)/(s2-bs-b 1) (s2-b2s+2) ;

б) r6(s)=(s2-s-bl)/(s2-b2s-b2)(s-bl):

в) rc(s) = (s-l)/(s2-bs+l)(s2-b2s + 2); r) rd(s)= (s-b 1) (s2 2s-f2)/(sa -bs-b 1).

2-22 (§ 2.5). Примените процедуру, указанную в примере 2.5-2, для определения коэффициентов полинома знаменателя функции цепи третьего по-Рядка, имеющей максимально плоскую ФЧХ с наклоном -1. Проверьте пра>-вильность результата, используя табл. 2.5-1.