сопряженных полюсов, получаем окончательно узкополосную проксимацию, функции цепи Л^*п (р) в виде

0,025 ( 0,025\-

0,025 У2 -

0,025\-

0,025 / 0,025\-1Г ,0,025 . /, 0,025\

/J Яр2

= --. (17)

pi 4- 0,0707+ 2,0025 + 0,0707 р + 1,0000

Фактическая функция цепи (р), полученная путем непосредственного применения (9), совпадает с нефакторизованной формой (17) с точностью до заданного числа значащих цифр. В общем случае следует помнить: узкополосная аппроксимация дает

Таблица 2.4-5а

Коэффициенты полинома в знаменателе равноволновой (чебышевской) полосовой функции цепи вида l+aiS+fl2S+ ... +C2S -2+aiS -+s с нормированной средней частотой 1 рад/с и амплитудой пульсаций 1 дБ

6 8 10

.054887 .049417 .047641 .046841

2.002756 3.003096 4.003635

5.оо4ггг

.098696

BW - 0.05

.143015 6.007271

.187486 10.012670 .281290

4 6 8

.109773 .098834. .095281 .093682

2.011025 3.012364 4.014539 5.016888

.198160 I BW = 0.1 I

.266586 6.029106

.375703 10.050723 .564042

4 6 8

4 6 8 10

.219547 .197668 .190562 .187364

2.044100 3.049536 4.058157 5.067SS3

.399267 [bUVo

.577628 6.li675&

.757252 10.203387 1.139814

.548867 .494171

.476406 .468410

2.275626 3.309602 4.363481

5.4ггго4

li0497SS

BW=0.5

1.522045- 6.744189.

1.995441 11.302896 3.057699

Положение полюсов и коэффициенты квадратичных множителей (flo+Cis+s) равноволиовой (чебышевской) полосовой функции цепи с нормированной средней частотой 1 рад/с и амплитудой пулы:аций 1 дБ

хорошую точность до тех пор, пока ширина полосы равна или меньше одной десятой от средней частоты, т. е. Q должно быть больше или равно 10. Как пример значительных искажений в определении положения полюсов при нарушении условия применения узкополосной аппроксимации на рис. 2.4-6 показано действи-

Sплоскость

р-плоскость 1

Г

Т

г

о; 6)

Рис. 2.4-5. Пример использования узкопологаой аппроксимации

тельное положение полюсов ПФ и положение полюсов, определенное с помощью узкополосной аппроксимации для случая, когда ширина полосы равна 1,5 рад/с, а средняя частота - 1 рад/с. Фактическое и расчетное значения положения полюсов даны для ПФ восемнадцатого порядка (ФНЧ-прототип девятого порядка). На рисунке видна значительная ошибка в случае использования узкополосной аппроксимации.

Ш 2/J

/2 2

п

Рис. 2.4-6. Случай, когда узкополосная аппроксимация неприменима:

/ - фактическое местоположение полюсов ПФ; 2 - местоположение полюсов в соответствии с узкополосной аппроксимацией

Рис. 2.4-7. Схема цепи, реализующая максимально плоскую АЧХ ПФ шестого порядка, тюлученная преоб-разованием цепи яа рис. 2.4-2. Значения элементов даны в 0(Мах, генрп, фарадах

Преобразование (9) также можно непосредственно применять к определению значений элементов данной реализации цепи. В этом случае катушка с индуктивностью К генри, имеющая полное сопротивление Zh4(s)=-/(s, становится последовательным соединением катушки с индуктивностью К генри и конденсатора с емкостью 1 С фарад, имеющим полное сопротивление {р)==Кр+

k-KIP, конденсатор с емкостью К фарад, имеющий полную проводимость Yim{s) Ks, становится параллельным соединением конденсатора с емкостью К фарад и катушки с индуктивностью 1 С гЬнри, имеющим полную проводимость Уц (Р) =Кр+К/р. ] Например, цепь, реализующая максимально плоскую передаточную проводимость ФНЧ третьего порядка (см. рис. 2.4-2), можно непосредственно преобразовать в цепь, реализующую максимально плоскую передаточную проводимость ПФ шестого порядка с шириной полосы 1 рад/с и частотами среза на уровне 3 дБ, равными соответственно 0,618 и 1,618 рад/с. Схема, полученная в результате преобразования цепи, показана на рис. 2.4-7. Передаточную проводимость этой цепи можно найти сразу, если применить результаты преобразования, приведенные в табл. 2.4-2, к первому уравнению (5), откуда получаем

/о ipWi iP) = Hp/iP + 2р' + V + 5р^ + 5р^ + 2/7 + 1). (18) где Н=\. Итоговая сводка преобразований элементов цепи приведена в табл. 2.4-6.

Нормированные ФНЧ - ФВЧ- и ФНЧ-ПФ-преобразования, определенные в (2) и (9), связанные с соответствующим нормиро-

Изменение элементов цепи прн преобразовании частоты

Таблица 2.4-6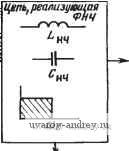

<РНЧ-<РВЧ-npeoSpaao--Вание

ч>бч

9НЧ- П<Р-преоВра~ зование

Цепь, реализующая П9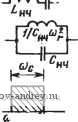

Г

9НЧ-П<Р-преобразование s=p + <f:/P

Цепь, реализующая РФ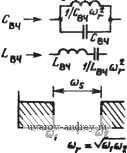

ванием частоты, можно применить в различной последовательности для получения любой желаемой комбинации средних частот и полос пропускания. Кроме того, если применить ФНЧ ПФ-преобразование к функции цепи верхних частот, получим режекторную характеристику, как видно из следующего примера.

Пример 2.4-1. Определение элементов схемы режекторного фильтра.

Пусть требуется реалшовать передаточную функцию РФ шестого порядка с резистивной нагрузкой 1000 Ом и полосой пропускания 1 кГц, средняя (геометрически) частота которого равна 5 кГц. В соответствии с техническим заданием, затухание в различных точках полосы пропускания должно быть не менее 15 дБ, а АЧХ в полосе пропускания должна €ыть монотонной. Предполагая, что будет использоваться вы.ражение (9), нормируем среднюю частоту и полосу пропуокания соответственно к 1 рад/с и 0,2 рад/с. Из примера 2.1-2 известно, что цепь, схема которой показана на рис. 2.4-2, имеет, как минимум, затухание 15 дБ на частоте 2 рад/с и монотонна в полосе задерживания. Денормируя по частоте элементы этой цепн с коэффициентом 2,5. получаем цепь, схема которой дана на рис. 2.4-8,а, которая имеет требуемое

rv-v-v.

/О т^ Пi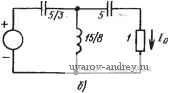

О

15l8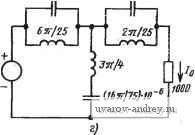

Рис. 2.4-8. Схема цепи, реализующая РФ в примере 2.4-1. Значения элементов даны в омах, генри, фарадах

затухание для всех частот выше 5 рад/с. Применяя ФНЧ-ФВЧ-преобразо-вание (2) к этой цепи, получаем цепь на рис. 2.4-8,6, которая имеет требуемое затухание (по отношению к его значению на высоких частотах) иа всех частотах меньших, чем 0,2 рад/с. Применяя преобразование (9) к полученной цепн верхних частот, получаем цепь, приведенную на рис. 2.4-8,е. Эта цепь имеет режекторную характеристику с шириной полосы 0,2 рад/с и средней (геометрически) частотой 1 рад/с. Денормируя по частоте элементы этой цепи с коэффициентом 2ii/5000, а затем шолное сопротивление с коэффициентом 1000,

п)лучаем конфигурацию цепи, показанную на рис. 2.4-8,г, которая удовлетворяет техничеоним требованиям.

\ ФНЧ - ПФ-преобразования, описанные в этом параграфе, так-ж'е можно непосредственно применять к эллиптическим функциям цепи нижних частот для формирования эллиптических полосовых функций, как показано в следующем примере.

.Пример 2.4-2. Эллиптическая полосовая функция. Пусть требуется реализовать ПФ четвертого порядка со средней частотой 1 рад/с, шириной полосы Пропускания 0,1 рад/с и амплитудой пульсаций в полосе пропускания 1 дБ затуханием е иже 17 дБ по отношению к максимальному значению ам1плитуды, равному единице гв полосе пропускания, для всех частот, лежащих за .пределами полосы шириной 0,2 рад/с. Из табл. 2.3-1 находим, что эллиптическая фушщйя цепи нижних частот второго порядка вида

Л' (s) = 0,139713 (s2 -f 0,07464102)/(s2 + 0,0998942 s -f 0,01170077) (19)

имеет максимальный модуль, равный единице, амплитуду пульсаций 1 дБ в полосе пропускания О ... /1 рад/с и затухание 17 дБ для всех частот, больших, чем частота среза 2 рад/с. Денормируя эту функцию по частоте с коэффициентом 0,1, изменяя ее полосу пропускания, которая становится равной О ... 0,1 рад/с и частоту среза, которая будет равна 0,2 рад/с. Денормированная функция

Л' (S) = 0,139713 (s2 -f 0,07464102) / (s -f 0,0998942 s -f 0,01170077). (20)

Положения полюсов этой функции следующие: s=-0,049947l±j0,0959482. Теперь можно найти полюсы ПФ путем непосредственного применения узкополосной апоронсимации. В результате получаем s=-0,0249736±j (1+0,479741). Эти полюсы соответствуют квадратичным множителям в знаменателе вида: s2+0,0499471s-f 0,906977 и 0,049947Is-f 1,0988733.

Используя (9), сразу преобразуем числитель к виду 2,07464Is-t-l, который можно представить множителями (s-t-1,313063) (s-1-0,761578). Таким образом, требуемая полосовая функция цепи будет иметь вид

i(s+ 1,313063) Яг (s +0.761578)

2+ 0,04994718 +0,906977 s2-f0,0499471 s-f 1,0988733 где произведение H\Hz равно 0,139713. Заметим, что в формуле (21) полюсы и нули 1сгруп1Пироваяы в два биквадратных множителя и подобраны так, чтобы в каждом множителе отделение нулей от полюсов было максимальным. Такое группирование уменьшает чувствительность (ом. гл. 3) функции цепи к изменению значений номиналов элементов при любой реализации цепи, а также помогает уменьшить чрезмерный разброс значений номиналов элементов при реализации.

2.5. Аппроксимация фазо-частотной характеристики

В предыдущих параграфах этой главы рассматривалась аппроксимация АЧХ. В этом параграфе займемся рассмотрением аппроксимации фазочастотной характеристики (ФЧХ),- т. е. будем Искать в плоскости комплексной частоты положение полюсов и нулей для функции цепи, которая имеет определенную фазочастот-

ную характеристику в установившемся состоянии при действии гармонического сигнала на входе. Прежде чем начать изучение такой характеристики, рассмотрим обобщенную рациональную функцию цепи N{s), которую можно представить в следующей форме:

N{s) = A {s)/B {s) = [m{s) + щ (s)]/[m, (s) + щ (s)], (1)

где mi (s) и tii (s) - соответственно четные и нечетные части полинома Л(5) в числителе, а m2(s) и 2(5) - соответственно четные и нечетные части полинома B(s) в знаменателе. Рассмотрим N{s) в условиях установившегося состояния при действии гармонического сигнала, т. с. сделаем подстановку s=jtu; тогда miQto) и тпгС] *)), будучи четными, окажутся вещественными, а ni(j(u) и n2(j( ), будучи нечетными, окажутся мнимыми. Следовательно, функция iVQto) запишется в виде

N{\(ii\- (j ю)-Ь j Im Л (j со) (j оз)-Ь/г, (j оз) ,2)

Refi(ja5) + jImB(jo5) г (j ю) + (j oj)

Выделяя вещественную и мнимую части путем домножения числителя и знаменателя на сопряженную для знаменателя величину тгО'со)-ПгО'к ), получаем

где для удобства убраны скобки, указывающие на функциональную зависимость величин и щ. Тогда фазу или аргумент Л/(jco) можно записать так:

arg N (j со) = arctg? = arctg mn-rnn, Re (j oj) J mi пц. -

Теперь удобно определить функцию Л(ю):

А И = tg [argN(i (0)] = - . (5)

Из (5) можно сделать вывод, что функция Л(ю) должна быть нечетной .рациональной функцией, т. е. отношением нечетного полинома к четному. Это требование должно быть не только необходимым, но и достаточным для определения рациональной функции цепи N(s) по известной Л(ю). Чтобы показать достаточность этого условия, сформируем вначале функцию 1+Л(ю). Используя (5), получаем

Из формы правой части приведенного соотношения можно сделать вывод, что числитель функции l+j/4(s/j) должен содержать в виде множителя нули и отображенные в правую полуплоскость полюсы функции цепи N{s), которая связана с функцией Л(ш) с помощью (5); Задавая эти множители в любом желаемом виде, согласующемся с требованием устойчивости, удовлетворяем достаточным условиям, как это видно из следующего примера.

I Пример 2.5-1. Определение функции цепи по ее аргументу. В качестве пйямера процедуры, указанной выше, рассмотрим функцию

\ / ((в) = (-0)3+11 (в)/(5(в2-15). (7)

I Отсюда видно, что

1 + j Л (05)

-J053 + 5052+j И 05- 15

(o=s/j 5 0)2-15

s3 5s2+ lis-15 (o=s/i -5s2-15

Числитель правой части этого равенства представляется в шиде (5-3) X (s2 2s+5). Приравнивая (s-3), к (mi + m), а -2s-f5 к Шг-Пг, получаем

;V(s) = (s-3)/(s2+2s + 5). (9)

Для этой функции цепи tg[argA(jo5)] определяется как функция Л(о5) в (7). С другой стороны, можно было бы представить множитель (s-3) как (/Иг-П2), а множитель (s-2s-t-5) как mi+n\ и получить еще одну функцию

iV(s)= - (s2-2s+5)/(s + 3), (10)

имеющую ту же самую ФЧХ. Наконец, можно представить (s-3),(s2-2s-t-5) как mz- 2 и 1 как mi+n\ и получить

Af(s) = -l/(s+3)(s2 + 2s + 5), (И)

т. е. еще одну (третью) фувкрию цепи с такой же ФЧХ. Для всех трех ф.унк-ций цепи tg[argA(jo5)] представляет собой функцию A{isi), определенную в (7). 4

При обсуждении аппроксимации АЧХ в предыдущих параграфах цель состояла в том, чтобы сохранить амплитуду в полосе пропускания постоянной с некоторой точностью. Цель аппроксимации ФЧХ, однако, несколько отличается от этой. Для многих случаев можно определить эту цель, исследуя понятие идеальной передачи. Чтобы обеспечить для цепи идеальную передачу некоторого произвольного входного возбуждающего сигнала e{t), было бы достаточно иметь в выходном сигнале r{t) то же самое информационное содержание, т. е. ту же самую форму сигнала. В таком случае существуют только две операции, которые допустимо было бы провести над сигналом e{t), а именно: масштабное преобразование и временной сдвиг (или задержка). Следовательно, можно определить идеальную передачу с помощью соотношения

r(,t)Ke{t-Q, U>Q. (12)

Другими словами, форма выходного сигнала будет идентична форме входного за исключением того, что амплитуда умножается на /С, а сигнал задерживается на время U. Полагая, что е() =0 Для /<;0 и преобразуя по Лапласу выражение (12), получаем (s) =C£(s)e-* где R{s) и E{s) соответственно преобразования Лапласа от r{t) и e{t). Принимая s=j i), получаем далее

.;?/g = iV(j©) = /Ce-J , (13)

где и - выходные и входные фазоры, а Л/(jco) - функция цепи. Из (13) видно, что для идеальной передачи требуется, чтобы \N{](>)) \=К (это значит, что амплитуда должна быть постоянной и независимой от частоты), а arg/V(jco) =-соо (т. е. фаза должна быть прямо пропорциональна частоте).

Рассмотрим теперь, как можно аппроксимировать линейную фазу, которая, как показано выше, обеспечивает идеальную передачу в заданной полосе частот. Для функции цепи нижних частот один из путей получения желаемой линейности - добиться того, чтобы первая производная ФЧХ была отлична от нуля и как можно больше производных более высокого порядка были бы равны нулю при © = 0. Этот подход аналогичен тому, который используется для получения максимально плоской АЧХ в § 2.1. Полагая, что обобщенная функция цепи нижних частот

(S) = I /( о + 1 S + s2 -Ь Сз 5 -Ь Й4 S* -Ь...), (14)

получаем соответствующую ФЧХ в виде

arg N (j со) = arctg (15)

Для ее разложения можно использовать следующий ряд:

arctgx = x---х^ + - х\.. (16)

Пример осуществления этой процедуры дан ниже.

Пример 2.5-2. Определение линейной ФЧХ. Рассмотрим функцию цепи нижних частот второго порадка

N{s)=l/{s + aiS+ao). (17)

Тогда аргумент ее, т. е. ФЧХ, можно выразить в виде

arg N (j CD) = - arctg - , ° . (18)

Ha основе (16) можно записать

argA ] со =- , \, + - ,-г- -....

Используя биномиальное разложение н проводя упрощения, получаем

arg Л' (j со) = -- 05 + во

V о Ч J

оэ -... (19)

Обозначая Oi/ao=o и .приравнивая в (19) коэффициент ори 05 нулю, обеспечим лгинейность фазы argA(jcu)=-cofo. В результате этого получаем следующие соотношения:

ао = ЪЦ1; oj = 0 (20)

Например, для fo=l потребуем, чтобы ао~3 и ai=3. Таким образом, функция цепи нижних частот второго порядка, имеющая линейную максимально плоскую ФЧХ с ща1клоном -11 (при постоянном токе), имет вид

A?(s)= l/(s2 + 3s-b3). ♦ (21)

Распространяя приведенную выше процедуру на функции цепи нижних частот более высокого порядка, получаем последовательность полиномов, известных как полиномы Бесселя. Фильтры, для формирования функций цепи которых используются эти полиномы, называются фильтрами Томсона [7]. В общем случае для таких фильтров коэффициенты знаменателя (14), соответствующие линейной ФЧХ с наклоном -1 (групповое время прохождения (ГВП) равно 1 с при постоянном токе), можно найти из соотношения

{n-k)\ k = 0,\,2..... n-1, (22)

2 -*й! {n - k)\

где n - степень знаменателя. Коэффициент для старшего члена равен единице. Значения соответствующих коэффициентов полиномов, корни и квадратичные множители приведены в табл. 2.5- 1. Для получения полиномов знаменателя, начиная с Bi(s)=s + \ и £2(5) =54-3s+3, можно использовать рекуррентную формулу

В, (S) = (2п -1) В„ 1 (S) Ч- 2 (S). (23)

Фактические характеристики, обеспечиваемые функциями, табулированными в табл. 2.5-1, отклоняются от идеальных как по линейности фазы, так и по постоянству амплитуды, что видно из рис. 2.5-1. Их можно сопоставить с идеальными характеристиками путем оценки отклонения от идеальных ГВП в

Рис. 2.5-1. Отклонение фактических характеристик линейно-фазовой фУКкции нижних частот от идеальных

Идеальный ФактичестЛ

.э

5е

Иввальный Фактический

Таблии/а 2.5-la

Коэффициенты полинома знаменателя линейно-фазовой (томсоновской) функции цепи нижних частот вида aB+aiS+a2S+ ... -t-a is -i-f s с нормированным ГВП (при постоянном токе) 1 с