Применяя указанное преобразование и домножая числитель и знаменатель на р , получаем

Л^Бч iP) = Л^нч (1 /р) = Нр 1(а^ р + -Ь Й2 +... + on-i-Ы).

Очевидно, что п нулей в бесконечности функции Л^н^ (s) преобразуется в п нулей, расположенных в начале координат, функции iVB4 (/?).

а Ofi------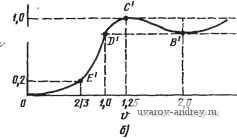

а 0,81,0 ifi

о;

Рис. 2.4-1. Нормированное ФНЧ-ФВЧ-шреобразовавие

Как пример, такого преобразования, рассмотрим две функции

iVH4(s) = /(s +2 + 25+1); Л^вч W(p + 2p?-f 2;p-f I). (5)

По виду функции Л^нч (s) сразу можно определить, что она является максимально плоской функцией цепи с частотой среза на уровне -3 дБ, равной 1 рад/с (см. табл. 2.1-3). Так как функция Л/вч (р) получается из Л/ч (s) с помощью преобразования s=l/p, то она является максимально плоской функцией цепи верхних частот третьего порядка с частотой среза на уровне -3 дБ, равной 1 рад/с. Для такой функции название максимально плоская относится, конечно, к ее поведению на бесконечно большой частоте.

Из процедуры преобразования, приведенной выше, видно, что для нормированной функции Баттерворта нижних частот с частотой среза на уровне -3 дБ, равной 1 рад/с, полюсы преобразованной функции цепи верхних частот занимают то же положение, что и для функции цепи нижних частот. Для других АЧХ, однако, это не так. Чтобы показать это, рассмотрим обобщенную функцию цели нижних частот, записанную в факторизованном виде

Н

(s-a)f\{s + a2iS-{-aii) 1=1

Таблица 2.4-16

Положение полюсов и коэффициенты квадратичных множителей (ao+ciis+s) равноволновой (чебышевской) функции верхних частот с нормированной полосой пропускания 1... оо радУс и амплитудой пульсаций 1 дБ

-.49763 . J .61190 J .97163

-.24833 ♦

г.огз59

-.14144- . 1.20570 .

-.09052 . -.S4S5S . 3.45431

-.06276,. -.30460 . 1.86087 .

J .99663 J 1.45786

J 1.00161 J 1.42540

J 1.00270 J 1.30393 J 2.1344-7

-.04605 . J 1.00262 -.19S99 J 1.22144 -.60309 ♦ J 1.98206 -4.86821

-.03521 ♦ J 1.00232 -.13779 ♦ J 1.16752 -.43773 . J 1-6SS9S -2.5091 . J 2.82099 I

-.02760 * J 1.00201 -.10274 J 1.13096 -.27831 . J 1.46416

-1.0S166 ♦ J 2.43274

-6.27626

.90702 1.00563

1.01368 3.57912

1.01182 2.32938

1.00935 1.79302 8.01660

1.00737 1.53033 4.33933

1.00589 1.38209 2.93376 14.23261

1.00479 1.26966 2.26016 7.02425

Положение полюсов и коаффицненты квадратичных множителей (co+flis+s) равноволиовой (чебышевской) функции цепи верхних частот с нормированной полосой пропускания 1... оо рад/с и амплитудой пульсаций 0,5 дБ

Применяя преобразование (2), получаем обобщенную фактори-зованную фунвдию цепи нижних частот

/ п/2

. 1=1

Отсюда сразу же можно найти квадратичные множители и полюсы, соответствующие случаю нижних частот. Табулированные значения для фильтров Чебышева верхних частот с амплитудой пульсаций, равной 0,5 и 1 дБ, приведены в табл. 2.4-1. Эти значения даны для тех же значений п, ао, а\, что и в табл. 2.2-2 в случае нижних частот.

Преобразование (2) можно непосредственно применить к элементам реализованной цепи. Иначе говоря, полное сопротивление нч (s) =s, определяющее катушку с индуктивностью К генри, становится в результате такого преобразования полным сопротивлением Zjj{p)=K/p, определяющим конденсатор с емкостью 1/К фарад. Аналогично этому, полная проводимость Унч(8)=/С8, определяющая конденсатор с емкостью К фарад, становится полной проводимостью У^ц{р)=К/р, которая определяет катушку с индуктивностью 1/К генри. В качестве примера применения преобразования (2) непосредственно к элементам реализованной цепи рассмотрим цепь нижних частот, реализующую функцию третьего порядка с максимально плоской АЧХ (рис. 2.4-2). Эта цепь при-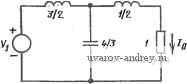

Ptic. 2.4-2. Схема цепи, реализующая максимально плоскую ампли-тудео-частотную функцию нижних частот третьего порядка. Значения элементов даны в омах, генри, фарадах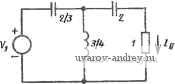

Рис. 2.4-3. Схема цепи, реализующая максимально плоскую амплитудно-частотную функцию верхних частот третьего порядка и иолученная преобразованием цепи на рис. 2.4-2. Значения элементов даны в омах, генри, фарадах

ведена в приложении А и имеет передаточную проводимость, заданную Л/нч(5) Б выражении (5) (см. выше), где Я=1. Применяя указанное преобразование к элементам цепи, получаем реализацию, показанную на рис. 2.4-3. Так как применение преобразования к элементам цепи дает те же результаты, что и применение преобразования к функции цепи в целом, можно сделать вывод, что передаточная проводимость этой цепи задается М^ц (р) в выражении (5), где Я=1.

Второе преобразование комплексной частотной переменной, которое рассмотрим в данном параграфе, что ФНЧ - ПФ-преобра-зование. Как и преобразование ФНЧ-прототипа в ФВЧ, описанное выше, это преобразование можно применять к любому типу АЧХ, однако, когда оно применяется к характеристике ФНЧ, то получается характеристика ПФ. Преобразование имеет следующий общий вид:

s = (l/W)[(p2 + a)2)/p], (8)

где S - переменная ФНЧ-прототипа, р - переменная ПФ, BW - ширина полосы пропускания (предполагаем, что функция цепи нижних частот имеет нормированную ширину полосы, равную 1 рад/с), соо - средняя частота результирующей полосы пропускания. Для удобства определим нормированное ФНЧ - ПФ-преоб-разование в виде

s = {p+\)lp, (9)

в котором средняя частота равна 1, а ширина полосы полосовой функции цепи должна быть равна ширине полосы ФНЧ. Решая ф) относительно р, получаем

p = s/2± У {s/2f- 1. (10)

Ограничиваясь рассмотрением случая установившегося состояния при гармоническом воздействии, т. е. полагая s = o+jco и принимая 0=0, найдем из (10) для p = + jt), что и = 0, а v определяется выражением

t; = co/2±l/(co/2)2+l. (11)

Следовательно, мнимая ось в s-плоскости преобразуется в мнимую же ось в р-плоскости. Природу преобразования можно уяснить', если заметить, что в соответствии с (10) точка s = 0 преобразуется в две точки p=+jl и р=-jl. Аналогично этому точка s=oo преобразуется также в две точки р = 0 и р = оо. Используя (И), можно видеть, что любая произвольно взятая на положительной мнимой полуоси s-плоскости точка, определенная как s = =j<Bi, преобразуется в две точки jf2 и -jti на р-плоскости:

-z;i = coi/2-]/7i/2)2-t-I; v = oyf2 + V{(oj2r+l, (12)

где vi и V2 положительны и V2>V\. Точка -jcoi на s-плоскости аналогично преобразуется в две точки j&i и ]V2 р-плоскости. Рассмотрим теперь более подробно точки Vi и V2. Из (12) получаем

&iz;2=l; Wg-&1 = %. (13)

На основе (12) и (13) можно сделать вывод, что любая частота АЧХ ФНЧ преобразуется в две частоты АЧХ ПФ и что эти

Наиболее точно и корректно это можно сделать, рассмотрев характери-стини соответствующего конформного преобразования, геометрическая интер-.претация которого сводится к двулистной римановой поверхности, см., например, [\*\.-Прим. пер.

частоты имеют следующие свойства: 1) их среднее геометрическое является средней частотой полосы пропускания; 2) их разность равна частоте среза ФНЧ. Следовательно, ширина полосы АЧХ ПФ равна ширине полосы АЧХ ФНЧ.

Как пример, подтверждающий эти выводы, рассмотрим преобразование АЧХ ФНЧ с полосой пропускания на уровне -3 дБ, равной 1 рад/с. Частоты Vi и V2, определяющие щирину полосы АЧХ ПФ на уровне -3 дБ, находятся из (12) и равны 0,618 и 1,618 рад/с. Очевидно, что эти значения удовлетворяют соотношению (13). Более подробный пример проведения преобразований АЧХ ФНЧ-прототипа в АЧХ ПФ показан на рис. 2.4-4, где рассмотрена равноволновая характеристика. Для лучшей иллюстрации этого преобразования характеристика ФНЧ расширена симметрично в область отрицательных частот. Соответствующие точки исходной и преобразованной характеристик обозначены буквами А, В,...А', В',...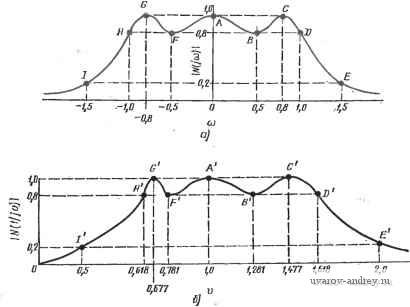

Рис. 2.4-4. Нормиррованное ФНЧ-1ПФ-треобразо1ваяи€

Рассмотрим теперь, что произойдет, если преобразование (9) применить к обобщенной функции цепи нижних частот (3). После цомножения числителя и знаменателя на р получаем

п(Р) =

нр;

> +й1Р -(р2Ч- 1) + й2р (рН1)Н-..+й„ 1Р(рЧ1) ~+(рИ1)

(14)

Получаемые в итоге обобщенные полиномы в знаменателе для типичных значений п приведены в табл. 2.4-2.* Каждая получаемая полосовая функция цепи имеет п-кратный нуль в начале координат и п-кратный нуль в бесконечности. В табл. 2.4-3 - 2.4-5 приведены некоторые определенные значения коэффициентов полиномов в знаменателе, корни и квадратичные множители различных полосовых функций цепи.

Так как степень полинома в знаменателе полосовой функции цепи, полученной с помощью ФНЧ ПФ-преобразования (9), удваивается по сравнению со степенью полинома в знаменателе исходного ФНЧ-прототипа, факторизация возможна в общем случае только благодаря использованию машинных программ нахождения корней полиномов.

Исключение из этого общего правила представляет случай, когда ширина полосы преобразованной полосовой функции цепи много меньше, чем ее средняя частота. В этом случае в качестве некоторой дополнительной к преобразованию (9) процедуры можно использовать непосредственное преобразование положения полюсов ФНЧ-прототипа, создавая, таким образом, полосовую функцию с уже факторизованным полиномом в знаменателе. Эта процедура соответствует узкополосной аппроксимации. Чтобы показать, <ак она действует, предположим, что средняя частота ПФ должна быть равна 1 рад/с. Определим теперь некоторую промежуточную переменную р' с помощью соотношения

Р = Р' + П, (15)

где р - комплексная частотная переменная ПФ. Это преобразование переносит начало координат р'-плоскости в точку j 1 в р-плоскости. Подставляя это преобразование в (9) и используя биноминальное разложение, получаем

s=(р' -f j 1)+W+j 1) = (P + j i)-]7(i +P7j) =

= (P + 3 l)-3 (1 -Pll + ...)- 2p, (16)

где последний член в (16) является линейным приближением, пригодным для р' 0, т. е. в окрестности средней частоты jl в р-плоскости. Это соотношение, наряду с (15), определяет узкополосную аппроксимацию, которая может быть непосредственно применена к положению полюсов в s-плоскости (ФНЧ) для определения их положения в р-плоскости (ПФ). Сравнивая относительное положение полюсов в р-плоскости и точки р = 1 с относительным положением полюсов в s-плоскости и начала координат, видим, что в обоих случаях угловое положение их одинаково, но при этом полюсы в р-плоскости расположены в 2 раза ближе к точке, относительно которой проводилось сравнение.

* Общий алгоритм определения коэффициентов полосовых функций цепи по их ФНЧнпрототипу .можно 1найти в работе Хьюлсмана [6].

Таблица 2.4-2

ФНЧ-ПФ-преобразование с нормированной средней частотой полосы пропускания 1 рад/с

ao + a,s + - + a,-,s +i

, W

1 + bp+bp + + Ь^р^ - + ьу -* + р^

Таблица 2.4-Sq Коэффициент полинома в знаменателе максимально плоской (баттервортовской) полосовой функции цепи вида

С нормированной средней частотой 1 рад/с

.670711 2.602566

.100000 3.005000

.130656 4.008536

.161803 5.013090

200125 I EW 0.05 j

.39Р296 6.01707

.evibsa 10.039291 .972130

.141421 2.010000 .200000 3.020000 .261313 4.034142

.401000

BW = 0.1

.786551 6.068384 .323607 S.052361 1.299663 10.157406 1.952123

.282843 2.040000 .400000 3.080000

.808000

BW = 0.2

.522625 4.136569 1.588781 6.274737

.647214 S.209443 2.630743 10.633506 3.967379

.707107 2.250000 l.OOCOOO 3.500000 2.125000

BW - 0.5

1.306563 4.8535S3 4.246330 7.769607

1.518034 6.309017 7.126644 14.129305 11.048471

Патсы

-.01799 .J 1.01768

-.01737 .J .98232

-.01277 .J 1.02181

-.01223 .J .97851

-.02500 .99969

-.02332 .J 1.00935

-.02288 VJ .99021

-.00979 .J 1.02332

-.00935 *J .97712

-.02052 *J 1.01460

-.01993 .J .98521

-.00791 .J 1.02403. -.00754 .J .97648

-.02500 *J .99969

-.03661 1.03536--.03411 .J .96465

-.02608 .J 1.0,4393 -.02392 .J .5732 r.05000 *J .99875

-.04708 .J 1.01825 -.04531 .97998

-.02002 *J 1.04708 -.01825 .95469

-.04164 .4 1.02900 -.03926 .J, .97023 -.01618 *J 1.04856 -.01472 .J iS5346 -.05000 .J .99875

1.0399 .96526

1.0445. .95762

i.ooood

1.01932 .98104

1.04728 .95486

1.02983 .97103

1.04870 .95356

1.00000

1.07330 .93170

1.09046 .91704 1.00000

1.03905 .96242

1.09677 .91177

1.06058 .94288

1.09975 .90930

1.00000

.03598 .03473

.02554-.02446 .05000

.04664 .04575 .01958 .01869

.04105 .03986 .01582 .01508 .05000

.0 7321 .06821

.05216 .04764 .10000

.09416 .09062 .04003 .03650

.08328 .07852 .03237 .02943 .10000

-.07571 1.07072 -.06571 *Л .92930

-.05432 *J 1.08911 -.04568 .91590

-.10000 .93499

.09594 ♦J 1.03473 .08884..95820 .04179 1.0959Z .03475 ♦J ,91115

.08566 .J 1.05724 ,07614 .J .93969 ,03383 *J 1.09915 .02797 .J .90894 .10000 .99499

.20801 ♦J 1,17T26

.14554 ♦J .82371

-,15164- ♦J 1.23236

-.09836 .J .79935

-.25000 ♦J .96825

-.25357 tJ J.07359

-.20837 .J .88224

-.11729 .J 1.25306

-.07405 .J .79112

-.23225 .J 1.13770

-.17226 .84380

-.09517 .J 1.26289

-.05934 .78736

-.25000 .96825

1.15218 .86792

1.18911 ,84097 1.00000

1.07988 .92603

1.20279 .fi3l40

1.12510 ,88881

1.20927 982695

j.00000

1.42922 .69S68

1.54171

.64863 1.00000

1.21688 .82177

1.58391 .63135

1.34829 .74168

1.60395 .62346

1.00000

.15142 .13142.

,10864

,09136 .20000

.19187 .17768 ,06358 ,06949

,17133 .15228 .06766 .05595 .20000

.41602 .29108

.30328 .19672 ,50000

.50713 .41675 .23458 .14810

.46450 .34451 .19034 .11867 .50000

Положение полюсов и коэффициенты квадратичных множителей (oo+ais+s) максимально плоской (баттервортовской)

полосовой функции цепи с нормированной средней частотой 1 рад/с

в качестве примера использования этих выводов рассмотрим применение узкополосной аппроксимации для определения положения полюсов максимально плоской полосовой функции цепи, имеющей четыре полюса, ширину полосы 0,05 рад/с на уровне -3 дБ и среднюю частоту 1 рад/с. В s-плоскости положение соответствующих полюсов максимально плоской функции ФНЧ-прототипа, имеющего два полюса и ширину полосы 0,05 рад/с, таково: -0,05 K2±j0,05/ j/T (рис. 2.4-5,а). Положение полюсов в р-плоскости, определенное с помощью (15) и (16), соответствует -0,025/К2±]( 1+0,025/ 1/2) (рис. 2.4-5,6). Добавляя очевидные требования наличия двукратного нуля в начале координат и

Таблица 2.4-4а

Коэффициенты полинома в знаменателе равноволновой (чебышевской) полосовой функции цепи вида l--ais+C2s2+ ... +a2S -2+Cis ~i+s с нормированной средней частотой 1 рад/с

4 б

8 10

.071261 .062646 .059869 .058625

2.003791 3.003637 4.004292 5.004843

.125381 I EW 0.05 1

.1797.36 6.008587

.234662 10.014535 .353075

.142563 .125291 1119739 .117249

2.015162 3.015349 4.017169 5.019374

.251299

BW = 0.1

.360242 6.034375 .470306 10.058196

.706X16

б 8 Ш

.285125 .250583 .239477 .234498

2.060646 3.061396 4.068675 5.077495

.506891

BW = 0.2

.726636 6.137956

.946470 1С.сЗ?.СЗ£ 1.42S001

.712813 .626457 .598693 .586246

2.379051 3.363724 4.429217 5.484342

1.342376

BW - 0.5

1.924263 6.fie2125

в.508681 11.500059 З.б504бг

Положение полюсов и коэффициенты квадратичных множителей (oo+ais+s) равноволновой (чебышевской) функции цепи с нормированной средней частотой 1 рад/с и амплитудой пулы;аций 0,5 дБ