1.гО 60.9<.9

1.50 е5.1Э8

2.00 109.915

1.05- 54.60В-

1.10 *7.307

1.20 S83.887

1.50

2.00 145iO?5

г) Случай В-четные; амплитуда пульсаций в полосе пропускания 1 дБ л го, К.(дБ) ff Pi Of 5l

1,05 13.243 1.166586

1.10 18.140 1.30973Г

1.20 24.700 I.6O.4O0

1.50- 36.771 2.595517

г.ОО 49.156 4.716540

.422751 .043154

.403039 .061666.

.062727

.361063 .109356

.346975 .124305

J .627439 Jt.006305

J .574970 Jl.004223

J .523216 Jl.000117

J .465487 J .993062

J .435853 J .988442

.845502 .086309

.806078 .123336

.767109 .165455

.722126 .218712

.69794Э .248611

1.05 30.730 1.125244

1.500649

1.10 - 3S.342 1.246215 1.800145

1.20

1.50

.332474 ♦ J .436556 .107214 ♦ J .902829 .017380 ♦ Jl.0001-83

48.285

66.425

1.499501 2.364951

2.378628 4.189497

2.00 65.008 4.267406

8.001466

.308336 * J .124563 ♦ J .025165 ♦ J

.284782 * J .140216 * J .034509 ♦ J

.258566 + J .155955 J .047022 ♦ J

.245081 . J .163303 ♦ J .054402 . J

.391152 666975 .999425

.349826. .827910 .996231

,306851 ,780065 ,996256

,285837 ,753736 .994927

.664948 .214429 .034760

.616673 .249126 .050371

-56Q565 .260431 .069019

.517132 .311909 .094044

.490161 .326605 .108805

1.05

1.10

47.987

58.146

1.114416 1.252994 2.034525

1.229114 1.441163 2.557144

-.268114 ♦ J .329175

-.134219 ♦ J .760319

-.044114 ♦ J .952060

-.009435 ♦ J .999653

-.244564 . J .293222

-.141813 ♦ J .730432

-.056360 ♦ J .932329

-.013771 ♦ J .999245

.536228 .268437 .088223 .018870

.469176 .263626 .112720 .027542

д) Случай С - четные; амплитуда пульсаций в полосе пропускания 0,1 дБ

1.05 3.284 1.176045

1.10

6.478

1.3215

1.20 12.085 1.615455

1.59 23.736 2.611679

2.09 36.023 4.733595

-.041450 ♦ Л.062080 .082900

-1.142752 + Л.056906 2.285503

-.076408 * Л.069646 .152816

-1.041973 ♦ J .905418 2.083946

.128382 ♦ Л.115527 .256764

.953405 * J .756606 1.906811

.206296 + Л.136431 .412592

.863022 ♦ J .597833 1.726044

.817435 ♦ J .520713 1.634871 .253437 ♦ Л.142940 .506873

1.05 18.727 1.126696

.1.535284

1.10 26.230 1.248053

1.837658

1.20 36.113 1.501690

2.404505

1.50 54.202 2.381154

4.230449

2.00 72.761 4.270072

8.042806

-.789645 ♦ J .570579 1.579289 -.185878 ♦ J .993057 .371755

-.025910 ♦ Л.021602 .051819

.715339 ♦ J -476877 1.430677 .230107 + i .952094 .460214

.040931 + Л.029755 .081861

.646187 ♦ J .39851 1.292374 .269710 ♦ J .902237 .539420

.060077 ♦ Л.03Б657 .120154

-.572096 ♦ J .324068 1.144191 -.308434 ♦ J .836973 .616868

-.087368 ♦ Jl.049425 .174736

-.534998 * J .290136 1.069995 -.325870 ♦ J .799822 .651740

-.104187 ♦ Jl.055209 .208374

1.05 36.268 1.114839

1.259509 2.085094

1.10 46.399 1.229651

1.448643 2.608880

-.60*065 ♦ J .371382

-.257536 ♦ J .843660

-.076089 ♦ J .979591

-.015568 ♦ Jl.010441

-.541763 ♦ J .314616

-.276093 ♦ J .780152

-.023659 ♦ Jl.014703

-.100633 ♦ J .962426

1.208130 .515072 .152178 .031137

1.083525 .552186 .047318 .201267

е) Случай С-четные; амплитуда пульсаций в полосе пропускания 1 дБ

лах- 3) постоянной Ks, определяющей допуск на затухание в полосе задерживания, выраженной аналогично предыдущему; 4) нижней граничной частотой полосы задерживания Os. Из данных, приведенных в таблице, видно, что если заданы любые два из трех параметров 2) 3) и 4), то функция цепи данного порядка определена полностью.

Приме^р 2.3-1. Использование таблицы 2.3-1. Пусть требуется найти эллиптическую функцию цепи, удовлетворяющую следующим условиям: 1) полоса пропускания О ... 1 рад/с с .амплитудой пульсаций 1 дБ; 2) полоса задерживания соответствует частотам со>2 рад/с и обеспечивает минимальное затухание 34 дБ; 3) максимальное значение АЧХ равно единице в полосе пропускания. Используя разделы таблицы, соответствующие амплитуде пульсаций 1 дБ, видим, что условия 1) и 2) удовлетворяются функцией третье-го порядка. Используя табулированные полюсы и нули, можно записать искомую функцию в виде

Я (s-f 5.153209) .

(S+0,539958) (s2-Ь 0,434067 s -Ь 1,010594)

Чтобы удовлетворить условию 3), оценим Л^о=й'-5,153209/{0,539958Х Х1,010594)=9,443675Я=1, откуда получаем Я=0,105891. Следует заметить, что если для удовлетворения условий требуется использовать четную функцию типа А или В, то для определения Я следует брать JV(0) равной 0,89125 (амплитудный эквивалент-1 дБ), а не единице. Это происходит лотому, что четные функции имеют минимум амплитуды в .полосе пропускания на нулевой частоте, тогда .как нечетные имеют на ей максимум, ф

Порядок эллиптической функции цепи, требуемый для удовлетворения заданным условиям, легко определить по номограмме, приведенной на рис. 2.3-3 [3]. Как пользоваться номограммой, было показано на рис. 2.1-5 (см. объяснения в 8.2.1). Следует заметить, что для функций четного порядка номограмма дает требуемый порядок функции для случая А. Если необходимо использовать функции применительно к случаям В и С, то для удовлетворения заданным условиям может потребоваться порядок функции, на единицу больший найденного по номограмме.

Пример 2.3-2. Использование номограммы для эллиптических функций. Пусть требуется найти необходимый порядок эллиптической функции цепи, уровень пульсаций которой в полосе тропускания равен 0,1 дБ, а минимальное затухание, обеспечиваемое для всех частот, в :1,5 раза больших частоты среза, .составляет 40 дБ.

Из рис. 2.3-3 находим, что требуемый порядок функции равен пятя. Сравнивая полученное значение с требуемым порядком функции по аппроксимации по Чебышеву и Баттерварту для удовлетворения тех же условий, находим, используя рис. 2.2-5 а 2.1-4, что он должен быть равен 8 и 17 соответственно. .Этот пример наглядно демонстрирует преимущества эллиптической функции в случае необходимости формирования АЧХ с крутым спадом, ф

10--8 -6 - if -

2 --

B,f 0.2-O.l-.r

0,06;:

O.Bt- -0,02--0,01--0,005- -

m .-m-

m--mr

10ll-\

BO-r 70-,r 60-} 50- -

zo\ 6

Z - -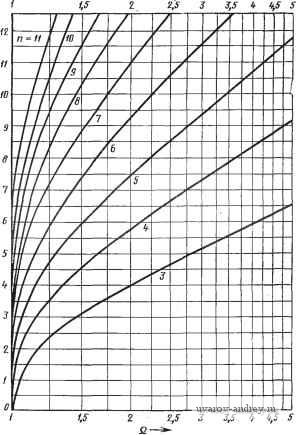

/ --

Рис. 2.3-3. Номограммы для определения порядка эллиптических функций

В этом параграфе была рассмотрена одна из наиболее полезных в случае создания фильтров с крутым спадом АЧХ функций - эллиптическая. Так же, как и определенные ранее функции Баттерворта и Чебышева, эллиптическая функция определяется для АЧХ ФНЧ. В следующем параграфе увидим, как все эти три характеристики можно использовать для фильтров верхних частот и полосовых.

2.4 Преобразование комплексной частотной переменной

Б предыдущих параграфах этой главы были рассмотрены три метода аппроксимации АЧХ. Все методы рассматривались применительно к функциям цепи нижних частот. В этом параграфе покажем, как эти типы аппроксимации можно применить к други11

типам функций цепи, таким как функции цепи верхних частот, полосовые и режекторные. Такое применение методов основано на использовании преобразований, осуществляемых над комплексной частотной переменной. Обсудим применение этих преобразовании с трех различных точек зрения: 1) их влияния на АЧХ; 2) влияния на функции цепи и 3) влияния на элементы данной реализации цепи.

Первое преобразование комплексной частотной переменной, которое будет описано, называется ФНЧ - ФВЧ-преобразованием.

Пусть s = a+3cu является исходной комплексной частотной переменной, а p = 4-jf- результирующей преобразованной комплексной частотной переменной; тогда указанное преобразование определяется в виде

S --= а + i со = со2/р = to2/(H + j у) = со2 [(ц j v)l{u -f (1).

где coo - постоянная. Если в этой связи ограничиться только случаем установившегося состояния при гармоническом воздействии подставив а=0, то приравнивая вещественные и мнимые части в-(1), получаем, что jco=-j<oV. Таким образом, положительная и отрицательная мнимые полуоси в (исходной) s-плоскости становятся соответственно отрицательной и положительной мнимыми полуосями в (преобразованной) р-плоскости. Кроме того, начало координат и бесконечно удаленная точка меняются местами. В результате такой замены АЧХ ФНЧ на оси jco преобразуется в АЧХ ФВЧ на оси jw*. Под действием этого преобразования, как это можно видеть из (1), частота соо становится геометрическим центром, относительно которого располагаются точки соответствующих АЧХ на осях jto и \v. Например, если создб частота спада АЧХ ФНЧ на 3 дБ (по отношению к ее значению на нулевой частоте), то соответствующая ей частота спада АЧХ ФВЧ на 3 дБ (по отношению к ее значению на бесконечно большой частоте) Уздб , полученная с помощью преобразования (1), удовлетворяет соотношению создБ I [здБ I =cuV Часто для удобства полагают соо= 1 рад/с. Тогда можно определить нормированное ФНЧ-ФВЧ-преобразо-вание:

s=l/p. (2)

Для такого преобразования создб1 здб I- Пример применения такого преобразования к равноволновой АЧХ ФНЧ показан на рис. 2.4-1. Соответствующие значения на исходной и преобразованной характеристиках обозначены буквами А, В,..., Л', В',...

Рассмотрим теперь, что произойдет, если применить нормированное преобразование к обобщенной функции цепи нижних частот вида

Л^нч (S) = НЦоо -Ь 1S + Сг ++ s + s ). (3)

* Изменение знака не оказывает .влияния, так как АЧХ симметричны относительно начала координат.