Прежде чем решать это уравнение, определим некоторую комплексную функцию

11У = ы--jtj = arccos(s/i). (7)

Подставляя ее в (6), получаем

cos n(u-\-]v) = cos пи ch да-j sin пи sh да = ± j/e. (8)

Приравнивая друг другу вещественные составляющие в правых частях выражения (8), получаем cos пи chuv = 0. Так как chnv 1 для всех значений nv, то это равенство требует, чтобы созпы==0. Последнее можно записать в виде

Uf, = {2k-l)u/2n, k=l,2,3,...,2n. (9)

Аналогично, приравнивая мнимые части в (8) и учитывая, что для значений; и, определенных выражением (9), sinnu=±l, получаем

и = Arsh(l/e). (10)

где оставлены только положительные значения для v. Выражение (7) можно теперь представить в виде

S = j cos ( fe + ]&) = sin sh и -f j cos ch и. (11)

Это соотношение определяет полюсы произведения N{s)N(-s). Полюсы, лежащие в левой полуплоскости, присваиваются A(s), чтобы окончательно определить функцию цепи. Следовательно, полюсами N{s) будут Рк=(Ук+]т, где

а^=-sinUftshw !

©ft = cos ch i

и где UkH V определяются в (9) и (10).

Пример 2.2-1. Определение функции Чебышева. В качестве примера использования формул (9)-.(И) рассмотрим определение полюсо:в равноволновой функции цепи нижних частот второго порядка с пульсацией в полосе пропускания 3 йБ.

В этом случае п=2, и из (9) получаем: wi = m/4 и Ы2=Зя/4. Для пульсации, равной 3 дБ, 8=1 и из (10) находим d=0,441. Используя (12), полу-

1, k=l,2,...,n (12)

IV J

(13)

ai= - sin-sh 0,441 = -0,322; e>i = cosch 0,441 = 0,777 ;

02= -sinsh0,441 = -0,322 ; w = cos -ch 0,441 = -0,777. 4 4

Следовательно, функция цепи

N (s) = H/(s+0,322+i 0,777) (s-}- 0,322-j 0,777) = H/(s+0,644s+ 0,7074). 4-

(14)

Реализация равноволновой функции в виде пассивной цепи приведена в приложении А. Координаты полюсов и значения коэффициентов полинома знаменателя для различных значений п

Коэффициенты знаменателя, представленного в виде flo+fliS+QaS-i-... +unS -4-s равноволновой (чебышевской) функции с полосой пропускания О... 1 рад/с

Таблица 2.2-26 Положение полюсов н коэффициенты

Положение полюсов н коэффициенты квадратичных множителей (uo+eis+s) равноволновой (чебышевской) функции це нижних частот с амплитудой пульсации 0,£ и полосой пропускания О... 1 рад/с

цепи .5 дБ

Положение полюсов и коэффициенты квадратичных множителей (a+ais+s) равноволновой (чебышевской) функции цепи нижних частот с амплитудой пульсации I дБ и полосой пропускания О... 1 рад/с

приведены в табл. 2.2-2. Геометрическое местоположениеполюсов можно определить, если воспользоваться основным тригонометрическим соотношением smUk+cosUk= I. Подставляя в это соотношение значения sinUk и cosuu из (12), получаем

aVsh V + (oVch = 1 (15)

Это уравнение эллипса с центром в начале координат плоскости Pk с большой полуосью, направленной вдоль оси ординат и равной ch V, и малой полуосью, направленной вдоль оси абсциссы и равной sh V, как показано на рис. 2.2 - 3.

Эллипс, определенный выражением (15), может использоваться в другом методе нахождения местоположения полюсов равноволновой функции. Чтобы сделать это, задаем нормирование по частоте так, чтобы полоса пропускания соответствовала интервалу OtoWc, где tuc=l/chD. Тогда на основании (12) положение нормированных полюсов определится так:

Oft = -sin и th v; to = cos . (16)

Эллипс, соответствующий этим полюсам, имеет полуось, направленную по оси ординат, равную единице, и полуось, направленную по оси абсцисс, равную th v. Сравнивая положение полюсов, задаваемое в (16), с положением, задаваемым в (15) (см. §2.1), в случае максимально плоской АЧХ (для единичной полосы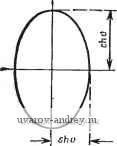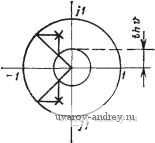

Рис. 2.2-3. Местоположение полюсав paiBHO-волновых по амплитуде функций

Рис. 2.2-4. Соответствие между положением полюсов максимально плоской и равноволновой функций

пропускания), можно видеть, что для заданного нормирования по Частоте равноволновой функции мнимые части соответствующих Местоположений полюсов обоих этих типов функций те же самые, тогда как вещественные части полюсов равноволновой функции Уменьшаются пропорционально множителю th v. В результате этого положения полюсов максимально плоской функции, имеющих одинаковые угловые координаты, могут использоваться для определения (графического) положения полюсов равноволновой функции путем проведения горизонтальных линий из точек пересечения радиус-векторов, соответствующих исходным полюсам, с единич-

ной окружностью и вертикальных линий из точек пересечения этих радиус-векторов с окружностью радиуса thv. Как видно на рис, 2.2-4, для функции второго порядка указанные пересечения горизонтальных и вертикальных линий определяют положение полюсов равноволновых функций. Ясно, что эти положения полюсов должны быть денормированы по частоте, если указанная функция должна иметь единичную полосу пропускания.

Рассмотрим теперь использование равноволновой аппроксимации для удовлетворения конкретных требований в частотной области.

Пример 2.2-2. Определение порядка функции Чебышева. В иримере 2.1-2 была определена максимально .плоская АЧХ, которая имела затухание 3 дБ относительно максимального значения на частоте со = 1 рад/с и- затухание не меньше 15 дБ для всех частот выше со=2 рад/с. Рассмотрим теперь использование равноволновой функции, удовлетворяющей тем же требованиям.

Подставляя е=1 в (1), устанавливаем амплитуду шульсаций 3 дБ, удовлетворяя, тем самым, требованиям на частоте со=1 рад/с. Так как равноволновая функция, аналогично максимально плоской, монотонна в полосе задерживания, то, если мы удовлетворяем указанному требованию на частоте to= =2 рад/с, мы удовлетворяем ему на всех более высоких частотах. Следуя (процедуре, в результате которой было лолучено выражение (16) в § 2.1, приходим к следующему требованию:

\N (j (i,)\ ax/\N(i2)I = [1 -f C\ (2)]l/2 > 5,623. (17)

Заметим, что в числителе левой части равенства (17) используем iV(jcD) тах, а н€ liV(0)l, как в (16), § 2.1. Причина этого заключается в том, что только равноволновые функции нечетного лорядка имеют максимальные значения при со=0, как непосредствеино видно из графиков на рис. 2.2-2. Подставляя выражение для С„(( ) из (36) в (17), получаем

[1 -Ь ch2 ( Arch 2)] 1 /2 > 5,623. (18)

Это неравенство можно разрешить относительно п:

п Arch [(5,6232-1)1/2]= 1,82. (19)

Arch 2

Таким образом, заданным требованиям удовлетворяет равноволновая функция второго торядка, хотя, как было показано в примере 2.1-2, для этих же целей требуется максимально плоская функция третьего порядка, так как она имеет меньшую скорость спада в начале полосы задерживания. ♦

Пример 2.2-3. Функция Чебышева, у которой е¥=й. В качестве другого примера, показывающего относительную большую эффективность равио1вол-новых функций по сравнению с максимально плоскими, рассмотрим задачу определения функции цепи с амплитудой пульсаций 0,5 дБ в полосе пропускания 0<со<1 рад/с и затухание не ниже 18 дБ для всех частот выше со=2 рад/с, В примере 2.1-3 было шоказано, что максимально плоская функция, удовлетворяющая таким требованиям, должна иметь пятый шорядок. Используя ре-

зультаты этого примера, можно показать, что равноволновая функция имеет порядок, определяемый неравенством

п >

Arch 2

Arch

(7,943)-1 \l/2 l\ 0,122 j

= 2,89,

(20)

T €. при равноволновой .алпрокоимации требуется только третий шорЯДОК функции; результатом этого будет, очевидно, значительное упрощение цепи.

Вычисления, аналогичные проведенным в предыдущих двух примерах, можно также осуществить с помощью номограммы на

А„п,АБ АЛА^ / 2 J < S 6 7 8 д 10

W-S S

о,г

a,oi-B,ai а,аи

SfiOS

3,0005-It) -

в,от5--

13В-.

30-.

70-60-.

soi so-.

0.S-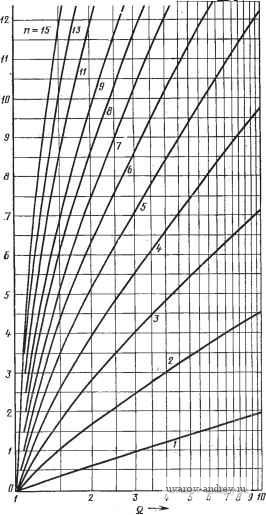

Ptic. 2.2-5. Номограмма для определения порядка равноволновой функция

рис. 2.2-5 [3]. Как пользоваться этой номограммой, было показано на рис. 2.1 - 5 (см. объяснения в § 2.1).

Рассматривая прекрасные результаты по затуханию в полосе задерживания, обеспечиваемые равноволновой функцией, как это было видно из двух вышеприведенных примеров, можно с уверенностью сделать заключение, что равноволновая функция должна использоваться в тех случаях, когда представляет интерес лишь АЧХ. В ряде случаев использования фильтров приходится рассматривать не только АЧХ, но и ФЧХ функции цепи. В этом отношении некоторые свойства максимально плоской функции цепи более предпочтительны, чем свойства равноволновой. Детально рассмотрим аппроксимацию ФЧХ в параграфе 2.5.

2.3, Аппроксимация амплитудно-частотной характеристики. Эллиптическая характеристика

В предыдущих параграфах этой главы были рассмотрены два типа аппроксимации АЧХ - максимально плоская и равноволновая. Характеристики обоих указанных типов аппроксимации можно записать в виде

\N{i<o)\=m/n+p\m, (1)

где Р^п{ч>)-полином, который в случае максимально плоской характеристики имеет видш, а в случае равноволновой - С* ((й) (полином Чебышева). В этом параграфе рассмотрим нескольк© другой тип АЧХ ФНЧ, когда полином Рп{а)) заменяется рациональной функцией /?п((в). Путем выбора определенной рациональной функции, названной рациональной функцией Чебышева, можно сформировать АЧХ, равноволновую не только в полосе пропускания, но и в полосе задерживания, как показано на рис. 2.3-1. Предполагается, что на этом рисунке величина Н из формулы (1) выбрана так, чтобы амплитуда 1Л^(ш) была равна единице. При заданном порядке фильтра результирующая АЧХ спадает (в переходной полосе) даже более круто, чем равноволновая харак-

/Голоса пропускания

Паласа задерживания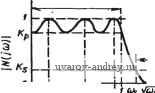

CJ2.

Рис. 2.3-1. Амплитудно-частотная характеристика, равноволновая как в полосе пропуокания, так и в полосе задерживания

В п-ереходной полосе, ели следовать установившейся у нас терминологии (см. замечание к с. 30). - Прим. пер. См. замечание яа с. 30. - Прим. пер.

теристика, обеспечивая, таким образом, наиболее крутой срез среди трех перечисленных типов АЧХ ФНЧ. Для определения вида рациональной функции /? ( )) необходимо в общем случае использовать эллиптические функции (функции Якоби) первого рода и полные эллиптические интегралы. Полученные таким образом функции часто определяют как эллиптические функции цепи. Учитывая, что первая оригинальная работа, посвященная таким функциям, была написана выдающимся немецким специалистом по теории цепей Кауэром, фильтры с эллиптической характеристикой часто называют также фильтрами Кауэра [5]

Прежде чем рассматривать фактически необходимую рациональную функцию i?n((B), которую будбм использовать, рассмотрим сначала связанную с ней функцию Я'п{а>)- Эта функция имеет две формы в зависимости от того, четно п или нечетно. Для четного п

(1-а>?а>)(1-а|а^)...(1-со/,а^)

где критические частоты Юг выбраны так, чтобы обеспечить желаемые равноволновые свойства. Для нечетного п

Анализируя функции, заданные в (2) и (3), можно заметить, что положения полюсов взаимообратны положению нулей и что RniUa) = l/Rn{(ii)- Вследствие этого значение Rnia) на любой частоте шо в полосе пропускания Огш^Шсреза взаимообратно ее значению на частоте 1/(Во в полосе задерживания (Взадерж^-о)<;оо. Таким образом, найдя значения частот ац таких, при которых Rn((i)) будет иметь равноволновую характеристику в полосе пропускания, автоматически определим равноволновую характеристику в полосе задерживания. Хотя функции i?n((o), заданные в (2) и (3), имеют желаемые характеристики (для надлежащим образом выбранных (Иг), они неудобны для использования, так как по-

Американскими авторами допущена существенная неточность. Рациоиаль-иая функция, яопользуемая для получения характеристики, именуемой в этой книге эллиптической, .была получена учеником П. Л. Чебышева Е. И. Золотаревым, а затем, действительно, была использована В. Кауэром для аппроксимации АЧХ фильтров. Поскольку фильтры с полиномиальной аппроксимацией именуются обычно по имени авторов соответствующих лоликомов фильт-рам1И Чебышева, Баттерворта и т. д., вполне логично именовать эллиптические фильтры фильтрами Золотарева. Такое название используется в отечественной литературе. Рациональная функция Чебышева (дробь Чебышева) иредставляет собой обобщение функции Золота1рева; ее отличие состоит в возможности произвольного расположения нулей передаточной функции фильтра, благода|ря чему АЧХ, сохраняя равноволновость в полосе пропускания, может удовлетворять различным требованиям по затуханию в различных частях полосы задерживания, т. е. равноволновость АЧХ в полосе задерживания в общем случае может н не иметь места (iOM. [14]).- Прим. ред.

лоса пропускания простирается от нуля до частоты, меньшей единицы, причем точное значение этой частоты изменяется в зависимости от п. Точно так же полоса задерживания начинается на частоте, большей единицы, причем ее значение также меняется в зависимости от п. Более удобная рациональная функция получается при выборе пары нижеследующих функций i?n(co), связанных с функциями, заданными в (2) и (3), частотным преобразованием. Четная функция

( 0)2 -( 0)2-. .( 2/2 -b/s)

i? ((B)=M

(1 о)2 0)2/{0s) (I -CU2 ... (1 -0)22 ls)

Нечетная функция

Ю ( ю2 -CO/tOs) ( o-- ( 4 -l)/2 - /tfls) (1 - 0)f/0)s) (1 -u/0)s) ... (1 -0) i,/2 ( 2/0)s)

где M w. N - некоторые множители, a ( - частота, с которой начинается полоса задерживания.

Нормирование, проведенное для функций, заданных в (4) и (5), обеспечивает полосу пропускания 0:о<:1 рад/с независимо от значения п и полосу задерживания в области частот caOs, как показано на рис. 2.3-1. Амплитудно-частотную характеристику эллиптической функции цепи можно теперь записать в виде

liV(j(o)=Я7[l-f?(fi,)], (6)

где Rn{<i>) задана в (4) и (5).

Рассмотрим отдельно случаи четной и нечетной функций. Если подставить выражение для нечетной /? ( )), заданное в (5), в формулу (6), заменить и на s/j и из полученного выражения отобрать только полюсы, лежащие в левой полуплоскости, и половину нулей на оси jco (см. § 2.1), то можно получить соответствующую эллиптическую функцию цепи нечетного порядка

(п-1)/2 -] /

(Co + fiiS-f ...-i-a iS --f fl s ), (7)

iVo(s) =

0 П +

где нули на оси j© расположены в точках s=±jQi- Степень полинома в знаменателе iVo(s) равна п, тогда как степень полинома в числителе - п-1. Модуль /Vo(j(u)l имеет (п-1)/2 максимумов в полосе пропускания (плюс один максимум в точке ю = 0) ( -1)/2 нулей передачи в полосе задерживания и нуль в точке (з) = оо. Пример АЧХ такой функции для я = 5 показан на рис. 2.3-2,а.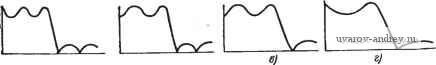

Рис. 2.3-2. Различные формы АЧХ эллиптических функций

Рассмотрим теперь случай, когда п четно. Используя четную Р„((й), заданную в (4), и преобразуя ее аналогично предыдущему, получаем первый общий вид эллиптической функции цепи четного порядка i

г п/2

I {a, + as+... + а„ д s - + as ). (8)

Будем называть его далее: случай А для четного п. Степени полиномов как в числителе, так и в знаменателе равны п. Модуль jjV(j(o) будет иметь п/2 максимумов в полосе пропускания, п/2 нулей передачи в полосе задерживания и ненулевое значение в точке (0 = 00. На рис. 2.3-2,6 показан пример формы АЧХ для п=4. Следствием того, что указанная эллиптическая функция конечна при (0 = 00, является то, что реализация ее в виде пассивной лестничной iLC-цепи возможна только тогда, когда в схеме используются связанные катушки индуктивности, т. е. трансформаторы. Это обычно нежелательно с точки зрения как стоимости, так и точности определения значений элементов. Таким образом, эта функция, как правило, рассматривается только для реализации активными /?С-фильтрами типа рассмотренных в гл. 4-7. Однако, если требуются реализации в виде пассивной цепи, необходимость в трансформаторах можно исключить путем модификации формы функции /? ((о), приведенной в (4). Модификация состоит в частотном преобразовании, сдвигающем в бесконечность самый высокочастотный полюс. В это'М случае функция будет иметь вид

(1-co2co2/cOs)...(l -( ;22 / s)

где величины (o, и (Os отличаются от аналогичных приведенных в (4), а величины (о'г отличаются от (Ог.

Подставляя полученное выражение в (6) и преобразуя аналогично приведенному выше, находим второй общий вид эллиптической функции цепи четного порядка

Будем называть его далее: случай В для четного п. Величины Йг и йготличаются, консчно, своими значениями от указанных в (8). Степень числителя равна п-2 (заметим, что индекс произведения i имеет начальное значение 2, а не 1), тогда как степень знаменателя равна п. Эту функцию можно реализовать без связанных катушек индуктивности, если сопротивления на зажимах Источника и нагрузки не одинаковы. Однако такое упрощение реализации достигается за счет того, что при заданном порядке и заданном затухании в полосе задерживания частота (Os - начало полосы задерживания - лежит несколько выше, чем в случае А. На