денная на рис. 7.3-11. В этой схеме, используется минимальное для данных реализаций -число операционных усилителей, оно имеет хорошую частотную характеристику с необходимым затухани-ем в полосе задерживания. В качестве звена первого порядка, вы-брана простая Т^С-цепь. Полюсы и нули спарены так, как показа-вз 6J2

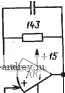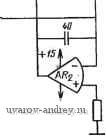
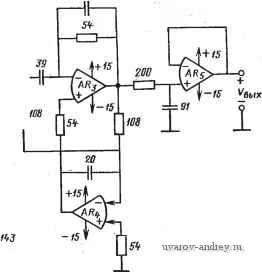ARf-Ai,LM3m ARg LF3SB

Рис. 7.3-11. Каскадная реализация эллиптичеоког-о фильтра пятого порядка. Значения элементов даны в килоомах и пикофарадах

НО на рис. 7.3-10. Расчетные формулы получены для звеньев второго порядка в предположении, что сопротивление Ri на рис. 7.3- 11 бесконечно велико. Тогда в соответствии с (27), § 7.1, имеем

Y) = .-9[s + (CiRjCsRs) il/R2R,CiCms +

VbX (s) Cj

+ s/RiCi + l/R2R5CiC2).

Общее выражение для эллиптической функции второго порядка можно записать в следующем виде:

Vo (sW, (s) = -Я„ (s2 + (o\)/(s-f SO) /Qp + CO%).

Поэтому, приравнивая (3), и (4), получаем

о)р = КТТадс; Qp=RiусЖЩс1

HoRJRs; (о^ = (Ор = 1/ 7Щ7.

Синтез фильтра начнем с денормирования по частоте передаточных функций отдельных звеньев. Последовательно получаем: для звена 1

Яl(s) = (s2-f8,688825-10 >)/(s2 + 83903s + 0,73176-10w), (9а) /р1 = 13,614 кГц; Qp, = 1,0195,/г!=46,912 кГц; (96)

(5),(6) (7), (8)

для звена 2

(S) = (§3 + 2,17323 10 )/(s + 29292 s + 1,35618 10 ), (1 Оа) /р2 =18,534 кГц, Qp2 = 3,97566,/,2 = 74,194 кГд; (106)

для звена 3

Яз (S) = 54900/(5 + 54900), /рз = 8738 Гц. (11а), (116)

Синтез каждого звена второго порядка проведен на основе выражений (5) - (8). В качестве операционных усилителей выбраны усилители в микросхеме LM3900 из четырех ИНУТ, собранных на одном кристалле. Для обеспечения режима по постоянному току на операционные усилители в LM3900 подается напряжение питания ±15 В (а не -f30 В). Следовательно, необходимо дополнительно включить резистор между землей и зажимом -f операционного усилителя Лг на рис. 7.1-И. Расчетное соотношение по постоянному току для Ах с бесконечно большим имеет вид

[1вых(0) + 15]/?1 = [1о2(0) + 15]/;?б. (12)

Аналогично, для усилителя Лг

[Vbx (0) + 15i/i?3 + [VBbix (0) + 15]/i?2 = 15/i?. (13)

где - сопротивление резистора, дополнительно включенного между землей и зажимом Ч- усилителя Лг. Тот факт, что входные зажимы усилителей микросхемы LM3900 подключаются к потенциалу -15 В, учитывается в (12) и (13). Если Fbx(0)=0, 102(0) = О, 1/,ь,х(0)=0, то

Ri=Rvi\lR=\lR+\lR. (14)

Для того чтобы обеспечить постоянный ток смещения, подаваемый на микросхему LM3900, меньший чем 500 мкА, Ri, R2, R5 и R должны быть больше 30 кОм. Если принять, как обычно, Ci = = €2, то получим значения R меньше 30 кОм. Таким образом, для получения больших значений R процедура синтеза должна быть следующей.

1. Выбрать удобное значение для Сг.

2. Вычислить Ci=2Q2pC2.

3. Принять /?i=/?5 = Qp/cOpCi.

. 4. Принять R2=R3=2Ri.

5. Выбрать R=R2l2=Ri.

6. Найти Сз=ЯоС,((Ор/(Ог)2.

На первом этапе синтеза получаем С2=40 пФ, Ci = 83 пФ, Ri = =/?5=143 кОм, /?2-/?з=286 кОм, i? = 143 кОм и Сз=7 пФ. На втором этапе получаем: С2=20 пФ, Ci = 632 пФ, i?i=/?5=54 кОм, 72=73=108 кОм, R=54 кОм и Сз = 39 пФ. На последнем этапе проводится синтез простой iC-цепи. Схема полученного в результате фильтра показана на рис. 7.3-11. Его частотная характеристика представлена на рис. 7.3-6. Настройка звеньев второго порядка осуществляется следующим образом.

1. Проконтролировать выходные сигналы каждого усилителя, чтобы убедиться, что получены требуемые режимы по постоянному току.

2. Удалить Сз и использовать Ci для настройки fp.

3. Использовать Ri для настройки Qp.

4. Включить Сз и настроить с его помощью fz-Измеренный собственный шум фильтра показан на рис. 7.3-6.

Он значительно ниже, чем шум структурно-перекрытой реализации варианта 2. При этом требуются И резисторов, семь конденсаторов и пять операционных усилителей. Однако с точки зрения гибридизации существуют только такие кристаллы, на которых можно разместить два операционных усилителя. Значения компонентов находятся в соответствии с гибридной технологией. Влияние ограничения скорости нарастания сигнала наблюдается для входных сигналов, превышающих 0,5 В (среднее квадратическое значение).-В конкретных условиях использования фильтра, однако, предыдущее звено ограничивает сигнал на уровне 0,3 В (среднее квадратическое значение). Следовательно, из-за ограничения скорости нарастания сигнала проблем не возникает.

Во втором примере рассматривается использование структурно-перекрытых реализаций для с;интеза восьмиполюсного ПФ Баттерворта со средней частотой 3000 Гц и шириной полосы 600 Гц. Звенья второго порядка реализуются с помощью универсального активного фильтра (УАФ), описанного в § 5.3. Чувствительность полученной реализации определяется экспериментально путем изменения частот fp и добротностей Qp отдельных звеньев на ±107о.

ФНЧ-прототип фильтра Баттерворта четвертого порядка находится из приложения А, схема его приведена на рис. 7.3-12,а.

Г

7,5т

L r

0,t330

I--- I

П

760 ~

I

Рис. 7.312. Схемы: a - ФНЧ-прототипа четвертого порядка, б - полосового фильтра восьмого порядка. Значения элементов даны в омах, генри, фарадах

Преобразуя его в полосовой прототип со средней частотой 1 рад/с и шириной полосы 0,2 рад/с, получаем схему на рис. 7.3-12,6. Для синтеза данного фильтра используются структурно-перекрытая реализация на рис. 6.3-4 и модификация УАФ на рис. 5.3-2 для реализации резонатора. Модифицированная схема показана

на рие. 7.3-13. Ниже приведены различные нормированные передаточные функции, которые должны быть реализованы с помощью УАФ:

Hi is) = - l/y (s) = -7.5185 + 1); (15a)

(s) = I/Z2(s) = 7,8860s/(s2+ 1) ; (156)

3 (s) = - I/F3 (s) = -5,4120 s/(s2 + 1); (15в)

Я4(5)=1/25)=1,91355/(52+ 1,91355+1). . (15г)

flv m тп вчщ НЧ m mv

Rg=w0kom

Rg = WKOM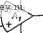

ЦИкОм

ЮВВпФ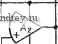

RiflBOKllM

ЮВОпФ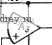

WOkOm

WDkOm

Puc. 7.3-13. Модификации универсального активного фильтра для реализации

резонаторного фильтра

Значения элементов схемы на рис. 7.3-13 следующие: для Hiis): J?i=oo; i?4=7.5185 Ом; C=l Ф; Я=1 Ом; (16а) для His): Ri=oo; 4=7,8860 Ом; С=1 Ф; i? = l Ом; (166) для Яз(5): 7?1 = схз; 4=5,4120 Ом; С=1 Ф; R=l Ом; (16в) для Я4(5): ;?1=1,91350м; /4=1,9135 Ом;С=1 Ф; R=l Ом. (16г)

Чтобы получить требуемое ненормированное значение С = = 1000 пФ, используемое в УАФ, емкости должны быть денормиро-ваны с коэффициентом 10. Так как требуемая денормированная частота составляет 6000 я, то денормированное полное сопротивление должно быть равно 53,052. Следовательно, все сопротивления должны быть умножены на 53,052, а все емкости разделены на 10. Полученная в результате реализация приведена на рис. 7.3

14. Схема УАФ и номера выводов соответствуют показанным на рис. 7.3-13.

Для реализации определялась чувствительность к изменению /рг и Qpi, где t соответствует t-му звену УАФ. Полученные результаты сведены в табл. 7.3-1 и 7.3-2. В табл. 7.3-1 даны значения

вх 333

й

,3 ft

.3 Н'5

t3 yAV-l 11 ♦

-15 +15

ft 13 УАЧ>-г 11 *

-15 +15

23 19

ft-я

УАР-3 11 *

-15 +15

t±)4c

К, Яг-

llf 13 yAV-if-11 *

-15 +15

11,11

11,11

11,11

Рис. 7.3-14. Структурно-перекрытая реализация полосового фильтра восьмого порядка, схема которого даиа на рис. 7.3-12,€. Сопротивления даны в килоомах ;

средней частоты /о полученной реализации для заданных изменений fpi или Qpi- В табл. 7.3-2 даны экспериментально определенные значения чувствителности /о к различным /pi и Qp,. Полученные результаты подтвердили тот факт, что передаточная функция больше зависит от чувствительности Sxivi, чем от Sxi [102].

Таблица 7.3-1

Процедура настройки фильтра на рис. 7.3-14

Результаты анализа чувствительности fo к изменению параметров схемы на рис. 7.3-14

Таблица 7.3-2

7-1 (§ 7.1). Используйте активный ?-фильтр, схема которого показана на рис. 7.1-!1,б, щля синтеза инвертирующего ПФ с (3=5 и if =100 кГц. Чему равно реализованное значение Я?

7-2 (§ 7.1). Покажите, что если Zi и на рис. 7.1-5,а будут равны R и 1/sC соответственно, а .{s) =/4oCOa/(s+cOa), то АЧХ при замкнутой петле обратной связи имеет полюс в точке -GB.

7-3 (§ 7.1). Используя схему на рис. 7.1-10, получите реализацию ФНЧ второго лорядка, имеющую Q=5 и /,i=20 кГц.

7-4 (§ 7.1). Повторите задачу 7-3 для реализации ПФ второго порядка.

7-5 (§ 7.1). Используйте схему на рис. 7.1-11 для пол1Д1ення реализации, аналогичной той, что рассмотрена в задаче 7-3, но имеющей комплексные нули в точках zfcjlOOat крад/с.

7-6 {§ 7.1). Применение операционных усилителей для создания искусственной индуктивности иллюстрирует рис. 3.7-6,а. Найдите модуль 1вхОш) и аргумент argZBx(jto) для этой схемы, если передаточная функция при разомкнутой петле обратной связи операционного усилителя имеет вид, приведенный на рис. 3.7-6,6.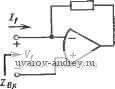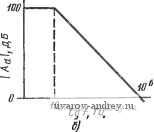

Рис. 3. 7-6. К задаче 7-6

7-7 (§ 7.1). В частотной характеристике схемы на рис. 3.7-7 наблюдается резонанс на частоте 12,7 кГц с добротностью 158. Полагая, что операционный усилитель имеет передаточную функцию при разомкнутой петле обратной связи, приведенную на рис. 3.7-6,6, найдите Vbhx/Vex, а также значения (Э и ш„ и сравните их с экспериментально наблюдаемыми значениями.

Рис. 3. 7-7. К задаче 7-7. Значения элементов даны в килоомах, микрофарадах

Rf=tO

VjblX

-о

7-8 (§ 7.2). Покажите, что Ивых (2Гс) для схемы на рис. 7.2-4 равно 0,298 В.

7-9 (§ 7.2). Найдите передаточную функцию (21), § 7.2, если ключи в

схеме на рис. 7.2-5,6 работают в противофазе, т. е. если при подсоединении

Сз к инвертирующему входу опбрацнонаого усилителя Ci подсоединяется к Vbi.

7-10 (§ 7.2). Получите выражение (24), приведенное о § 7.2.

7-11 (§ 7.2). Замените реализацию ФНЧ иа усилителях с положительным коэффициентам усилении на рис. 4.2-4 эквивалентной схемой, используя коммутируемые конденсаторы. Считайте, что К=1. так что Ra и Rb на рис. 4.2-4 соответственно бесконечно велико и равно нулю. Выразите Oi и че-раз заданные параметры фильтра Тс, ш„ и Q, используя соотношения ai= =Ci/C2 и а2=Сз/С4 и полагая, что Rt и Rs заменены коммутируемыми конденсаторами Cl и Сз.

7-12 (§ 7.2). а) Используя схему резонатора на рис. 7.2-7,6, реализуйте ПФ второго порядка с добротностью 100 и резонансной частотой f , равной 100 Гц. Примите тактовую частоту равной 100 кГц .и считайте, что Oi и 2 заданы соотношениями, принятыми в (36), (37), § 7.2.

б) Повторите указанную процедуру для !fn=5 кГц и той же тактовой частоты 100 кГц.

7-13 (§ 7.2). Используя схему на основе переменных состояния на рис. 7.2-9, реализуйте .ПФ второго порядка с добротностью 10 и /п = 1 кГц. Считайте, что величины Oi, Ог, оз и 04 определяются соотношениями: 0,= =Ci/Ci, OnC/Ci; аз=С'4/С'з и atCslCe- Примите, что 01=02, 04=!, а Гс=10-5 с.

7-14 (§ 7.2). Используйте метод выборки данных для реализации передаточной функции нижних частот Баттерворта четвертого порядка с частотой среза 5 кГц. Сопротивления источника и нагрузки должны быть равны 500 Ом каждое. Фильтр-.прототип можно определить по приложению А. Нарисуйте схему реализации и укажите значения емкостей всех конденсаторов. Используйте тактовую частоту 100 кГц.

7-15 (§ 7.2). Используйте метод выборки данных для синтеза схемы реализации, характеристики затухания которой показаны на рис. 3.6-iI2. Для аппроксимации указанной характеристики должна быть использована эллиптическая функция третьего порядка. Фильтр-прототип можно синтезировать, используя приложение А. Сопротивления источника и нагрузки должны быть равны 1000 Ом каждое. Тактовую частоту примите равной 100 кГц. Нарисуйте схему реализации и укажите значения всех емкостей.

7-16 (§ 7.2). Покажите путем определения Уз(в) через Vi{s) и ¥2(5), что схема с выборкой данных на рис. 3.7-16 реализует инвертирующую схему, интегрирует V2 и суммирует его с Vi. Предположите, что sTcl.

Рис. 3. 7-16. К задаче 7-16

ПРИЛОЖЕНИЕ А

Реализация пассивных фильтров нижних частот

в этом приложении представлены таблицы для реализации различных типов функций нижних частот. Первый тип фильтра - односторонне нагруженная сопротивлением лестничная цепь без потерь. Схемы се реализации с источником напряжения на входе показаны на рис. А-1,а (для функций четного порядка) и рис. А-1,6 (для функций нечетного порядка). Вид реализации с источником тока на входе показан на рис. А-2,а (для функций четного порядка) и рис. А-2,6 (для функций нечетного порядка). Значения элементов для (нормированных) фильтров Баттерворта, Чебышева (с пульсацией 0,5 и 1 дБ) и Томсона приведены в табл. А-

Рис. А-1. Схемы цепи для табл. A-I (источник напряжения на входе) для

функций:

а - четного, 6 - нечетного порядка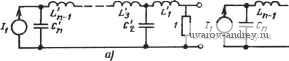

Рис. А-2. Схемы цепи для табл. А-1 (источник тока на входе) для функций: а - четного, 6 - нечетного порядка

Второй тип реализации - двусторонне нагруженные сопротивлением лестничные фильтры без потерь. Схема данной реализации показана на рис. А-3,а (для функций четного порядка) и А-3,6 (для функций нечетного порядка). Другая схема реализации дана на рис. А-4,0 (для функций четного порядка) и рис. А-4,6 (для функций нечетного порядка). В табл. А-2 приведены значения элементов для (нормированных) функций цепи Баттерворта, Чебышева (с пульсацией 0,5 и 1 дБ) и Томсона для случая равных сопротивлений. В этом случае не существует решений для функций Чебышева четного порядка В табл. А-3 приведены значения элементов для случая, когда отношение сопротивлений нагрузки и источника равно двум. В этом случае не существует решений для четных функций Чебышева с пульсацией 1 дБ.

Схема фильтра дли двусторонне нагруженных сопротивлениими лестничных реализаций без потерь эллиптических функций нижних частот показана иа рис. А-5. Другая схема реализации приведена на рис. А-6. В табл. А-4 и

Существуют, однако, таблицы для функций, близких к функциям Чебышева четкого порядка при равных нагрузочных сопротивлениях. Прим. пер.

Таблица А-1

Значения элементов лестничных НЧ прототипов без потерь с граничной частотой 1 рад/с, нагруженных с одной стороны, с характеристиками Чебышева (Ч), Баттерворта (Б), Томсона (Т). Элементы фильтров Чебышева даны для двух значений амплитуды пульсаций Да*

Элементы на рас. А-Га(че1пше) и рас. л-гВ{тчетиые)

2 3 4 5 6 7 8 9 10

0.9110 1.0118 1.0495 1.0674 1.0773 1.0832 1.0872 1.0899 1.0918

0.9957 1.3332 1.4126 1.4441 1.4601 1.4694 1.4751 1.4790 1.4817

1.7317 2.1111

1.3801

ЗлЕменты на-рас. MB (нечетные) а JK-Za (четше)

* Перепечатано с разрешения автора из работы [101].

А-5 даны значения элементов для различных уровней пульсации в полосе пропускания и различных порядков. Таблица А-4 соответствует реализациям нечетного порядка (фильтры с уровнем пульсаций 0,1 и 1 дБ) и четного порядка-при-двусторонней нагрузке равными сопротивлениями (случай с). Таблица А-5 соответствует случаю 6 (нагрузочные сопротивления не равны между собой) , дл.Я'.фцл^тррв. четного порядка (уровень пульсаций-в полосе пропускания 0,1-я1,0,дБ.): ; , . .

I-1-I-

-I 1 i т

о о-

Рис. А-3. Схемы цепей для табл. А-2 и А-3 для функций: а-четного, б - нечетного порядка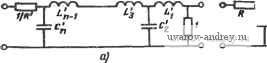

i -ror -----1 * -r-

Puc. A-4. Схемы цепей для табл. А-2 и А-3 для функций: а - четного, б - нечетного порядка

Таблица А-2

Значения элементов лестничных НЧ прототипов без потерь с граничной частотой 1 рад/с, нагруженных с двух сторон сопротивлением R=\ Ом, с характеристиками Баттерворта (Б), Чебышева (Ч), Томсона (Т). Элементы фильтров Чебышева даны для двух значений амплитуды пульсаций Ао*

Элепеиты иа рис. Л-За(четные) и А-Ы(нечетные)

C ig С, Ljo

0.4450 1.1111 1.5321 1.7820

0.3902 1.0000 1.4142

0.3473 0.9090

0.3129

3 1.5963

S 1.7058

7 1.7373

9 1.7504

1.0967 1.2296 1.2582 1.2690

1.5963 2.5408 2.6383 2.6678

1.2296 1.7058 1.3443 2.6383 1.3673 2.7239

Ч

1.2582 1.3673

1.7373 2.6678

1.2690 1.7504

3 2.0236

5 2.1349

7 2.1666

Э 2.1797

0.9941 1.0911 1.1115 1.1192

2.0236 3.0009 3.0936 3.1214

1.0911 2.1349 1.1735 3.0936 1.1897 3.1746

ч

lsl=lfiB

1.1115 1,1897

2.1666 3.1214

1.1192 2.1797

Ci .

Эленеяты ни puc. А-зе (нечетные) it A-fha (четные)

* Перепечатано с разрешения автора из работы [101].