Расчетные соотношения § 5.2 можно использовать.и для этой цепи, если заменить Ri на 1/Сг, где i=3, 4, 5, 6. К сожалению, недостатки реальных операционных усилителей делают эту реализацию непрактичной. Одна из причин заключается в том, что отсутствие обратной связи по постоянному току приводит к появлению избыточного напряжения смещения по постоянному току на выходе операционного усилителя. В общем случае требуется использовать ряд резисторов, что делает указанную схему на основе переменных состояния менее удобной для реализации в качестве фильтра с выборкой данных, чем схема резонаторного фильтра. Упрощенная реализация фильтра на основе переменных состояния по методу фильтрации с выборкой данных приведена в литературе [93].

Методы реализации фильтров с выборкой данных пригодны также и для других фильтров второго порядка, таких, например, как фильтры а усилителях с бесконечным коэффициентом усиления (см. § 5.1). Пример реализации ФНЧ на усилителях с бесконечным коэффициентом усиления и его изготовления на основе МОП-технологии можно найти в литературе [93].

В методах синтеза фильтров на основе моделирования пассивных цепей (см. гл. 6) также может использоваться техника дискретизации. Например, метод структурно-перекрытых реализаций (см § 6.3) очень удобен для использования дискретизации и часто дает прекрасные характеристики чувствительности. Чтобы убедиться в этом, заметим, что основной элемент такого фильтра - интегратор. Учитывая, что схема на рис. 7.2-6,е реализует дифференциальный интегратор, можно использовать в качестве прототипа схему с перекрытой структурой на рис. 6.3-2. Передаточная функция промежуточного звена структурно-перекрытой реализации дается выражением (1), § 6.3, и выражается в общем виде как

Vj{s)r.(s)[Vi(s)-l\{s)], (50)

где напряжения Vi, Vj и Vh располагаются последовательно вдоль лестничной структуры слева направо и могут быть либо эквивалентами токов, либо фактическими напряжениями. Если на рис. 7.2- 6,6 заменить V2 на Vi, Vi на Vj и вых на Vn, то из (23) можно получить

Vj (S) = [1/S (Т,/С;) Cj] [Vi (s)-V is)], (51)

где для s=jco, соГс!, a Ci и Сг на рис. 7.2-6,е заменены на Cj и Cj. Так как Tj{s) из (50), как правило, нормируется по полному сопротивлению к значению 1 Ом, а частота среза к значению 1 рад/с, то следует либо денормировать (50), либо нормировать (51), прежде чем сравнивать оба выражения. Предполагая, что определяется частота среза, получаем, что самый простой вариант- осуществить нормирование (51), которое сводится к нормированию тактовой частоты к величине Г'с, задаваемой соотношением вида

n=T,Q. (52)

При этом предполагается, что (50) нормировано к 1 рад/с. Поэтому ttj, т. е. отношение Cj к Q можно рассчитать по формуле

a,- = s[T,Q T;(s)] = C;/C-. (53)

Так как лестничная структура всегда нагружена сопротивлением, последний интегратор должен быть демпфированным. Заметим также, что последний интегратор не должен быть дифференциальным, так как нет петли обратной связи. В этих условиях схема на рис. 7.2-6,е может использоваться, если подсоединить Vi к вых. Используя обозначения, принятые в (51), имеем: Vj равно Vh-Таким образом, (51) можно записать следующим образом:

Vj {s)/Vt (s) = (sWi (s) = l/[s (Tjaj) + 1]. (54)

Если лестничная структура является фильтром m-ro порядка, то передаточную функцию последнего звена в общем виде можно записать так:

Vr,(sW-As)T{s)=l/{RLn + sLn)-V{GLn + sCn), (55)

где индекс п соответствует нормированным значениям компонентов. Если выбрать сопротивление Rlu равным 1 Ом или принять Сьп за 1 Ом, то можно использовать (54) и (55) для того, чтобы получить От ДЛЯ послсднего звена:

a = T,QjL = TMCn, (56)

где величины в средней и правой частях представляют собой элементы лестничного фильтра: сопротивление 1 Ом, включенное последовательно с нормированной индуктивностью Lmn и сопротивление 1 Ом, включенное параллельно с нормированной емкостью

Если лестничная структура нагружается с обеих сторон, то сопротивление источника равно Rs. Хотя сопротивление источника (и сопротивление нагрузки) может быть внешним по отношению к реализации, рассмотрим, какую модификацию необходимо провести в первом (крайнем слева) каскаде, для того чтобы включить сопротивление источника Rs. Возможны две конфигурации источника: по Тевенину или по Нортону. Передаточная функция первого каскада

(S) = Т[ (S) [Vi {s)~V, (s)] = [Vi (s)~V, is)]/[R,n + sLin]

= [Vi (s) - Vs (s)]/[Gsn + s Ci ]. (57)

К сожалению, необходимо формировать разность между входным и выходным сигналами звена 2, так что схему на рис. 7.2-6,6 нельзя использовать непосредственно. Однако дифференциальный демпфированный интегратор можно получить путем моделирова-ния демпфирующего резистора на рис. 7.2-6,е с помощью коммутируемого конденсатора. Полученная в результате схема показана на рис. 7.2-10. Так как она идентична схеме, содержащейся в об-

веденной пунктиром части рис. 7.2-7,а, то можно, используя (27), написать

() = .Ге(С./с:)!сХ iVAs)-VAs)], (58)

где ai = Ci/Ci и as=Cs/Ci. Нормируя Тс и сравнивая (57) с (58), получаем

1 = CJC[ = CiJTc Qn == LiJT, Q ; (59)

as = aisn = aiGsn. (60)

Пример 7.2-2. Реализация схемы примера 6.3-/ по методу выборки данных. Пусть требуется получить реализацию с выборкой данных для ФНЧ третьего порядка, сиитезированного в примере 6.3-1. Предположим, что тактовая частота равна 100 кГц, а частота среза фильтра -, 1 кГц (О„=2000зт).

Используя ту же схему нумерации элементов, что и на рис. 6.3-10, из (53) получаем

аз = (4000 я/З) 10-=0,0419; а2 = (6000 зт/4) 10 = 0,0471.

Если RLn=RL-l Ом, то (55) дает 01=400031-10-5=0,li257.

На рис. 7.2-М показана реализация, использующая выборку данных (или технику дискретизации). Интересно отметить, что емкости Си Ci и Сз выбираются произвольно: ли-

бо с учетом возможностей МОП-тех-

Рис. 7.2-10. Схема коммутируемого , ,

дифференциального демпф.ировашого нологии, либо с учетом других фак-

интегратора торов.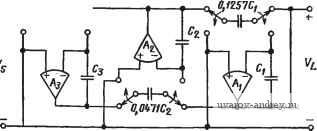

Рис. 7.2- . Схема коммутируемого структурно-перекрытого фильтра

Некоторые другие примеры использования техники дискретизации Для реализации структурно-перекрытых схем можно найти в литературе. Среди этих примеров есть двусторонне нагруженные ФНН;:Баттерворха .четвертого порядка [96].и Чебышева пятого по-

рядка [97J, а также двусторонне нагруженный эллиптический ФНЧ третьего порядка [97]. В этих работах показана также техника реализации нулей с помощью интеграторов (сумматоров) с-коммутируемыми емкостями.

Так как коммутируемый интегратор - основной элемент в технике реализации, представленной в этом параграфе, проанализируем его характеристики более подробно. Выражение (9) дает передаточную функцию коммутируемого интегратора в s-плоскости.-Если вых(5)/вх(5) =(s) и S выражсна через jco, то (9) принимает вид

Я(](0) = -=/=( )-?- . (61>

-е

Используя определение, данное в (12) для (Оо, и выражая тригонометрические функции через экспоненты, .получаем

-\4iTJ2

Я(](о)==-((о„Т,) -

2 j sin (q Гс/2) j ш

2 Sin (ш Гс/2)

©о

j ш [ /с sin (л /с)

(62>

Выражение (62) показывает,что фактическая передаточная, функция интегратора является произведением идеальной передаточной функции и неидеального множителя. Для лестничной структуры было найдено, что (Oo = CV7cCj = cXj/7c. Поэтому ml(o= = aj/c(2ji/). В примере 7.2-2, если /=/среза, которая была в 100 раз меньше fc, то (Oo/(o = 50aj/jt, что соответствует идеальному коэффициенту усиления интегратора на частоте /среза. Однако член в. скобках выражения (62) равен 1,00016 / -1,8°. Наличие запаздывания по фазе, равного 1,8°, может оказать существенное влияние на характеристики высокодобротных реализаций. Если тактовая частота возрастает до 1 МГц, то член в скобках выражения (61) становится равным 1,0000016 / 0,18°. Множитель в скобках. -Wlic, характеризующий задержку, можно исключить, если выходной сигнал интегратора передается на следующее звено сразу же как только произошло его изменение (мгновенная выборка). Этот факт обсуждался ранее, и в реализации на рис. 7.2-11 используется такая фазировка ключа, которая позволяет устранить задержку, т. е. исключить соответствующий член из (62).

Недавно был предложен интегратор, осуществляющий выборку-данных со скоростью, превышающей вдвое скорость выборки описанного выше интегратора. Его характеристика спадает до нуля на частоте, равной половине частоты тактового генератора [98, 99]. Это снижает искажения, вызванные эффектом наложения. Схема такого интегратора показана на рис. 7.2-12. Пусть в момент времени (п-\)Тс ключи находятся в положении, показанном на рисунке. Следовательно, Су заряжается до.напряжения vi{(n-\)Tc\,

2 - ДО напряжения V2[(n-1)7с]. На следующем такте ключи меняют позицию, и напряжение на Сг

v,inTc)V2[(n-l)T,]~VlinTc)~i-vAin-l)Tc]. (63)

Передаточная функция такого интегратора

(64)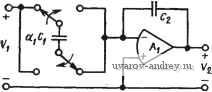

Рис. 7.2-12. Схема коммутируемого интепрато-ра с уменьшенным эффектом наложения

Заменяя s на j(o и С1/С2 на ыоТс, получаем вместо (64) 7V(j(o)=-5

(65)

Из (65) видно, что идеальной передаточной функцией такого :фильтра должно быть выражение -2(0o/j©, потому что скорость выборки фактически удвоилась. Видно также, что член, характеризующий задержку, для такого интегратора отсутствует.

Существуют другие ограничения для реализации с выборкой .данных, о которых мы только кратко упомянем. Одним из основных источников ограничений является операционный усилитель. Скорость нарастания выходного сигнала должна быть достаточно высока, чтобы имелась возможность почти мгновенно отслеживать .изменение выходного сигнала при переходе от одной выборки к ..другой. Приемлемое время перехода от одного уровня к другому лля тактовой частоты 100 кГц составляет примерно 1 мкс. Поэто му для усилителя, имеющего скорость нарастания 1 В/мкс, можно допустить изменение уровня выходного напряжения не более чем на 1 В, чтобы не ощущалось ограничение на скорость нарастания. .Так как усилитель переключается с частотой тактового генератора, то важно иметь хорошую переходную характеристику с минимально возможным временем установления. Если добротность фильтра велика, то влияние конечного коэффициента усиления операцион- ного усилителя может стать серьезным ограничивающим фактором [93]. Наконец, следует рассмотреть влияние теплового шума уси-..лителя и ключей. Кроме того, что усилитель должен иметь низкий уровень !шумов даже для обычных (аналоговых) активных RC-фильтров [100], нужно учитывать, что коммутируемые конденсаторы, моделирующие резисторы, генерируют тепловые шумы, средине квадратическое значение термо-ЭДС которых

Vc (СКВ) = VkT/C, (66)

гт kT - произведение постоянной Больцмана на температуру^ Видно, что шум коммутации можно минимизировать увеличением номинала С.

Использование техники дискретизации для реализации активных /?С-фильтров началось сравнительно недавно; возможно это. приведет к расширенному использованию активных фильтров. Кроме того, активные фильтры, реализованные таким способом, имеют несколько интересных свойств, к которым относится возможность' программировать фильтр, используя соответствующие тактовые частоты. Другим свойством является то, что поскольку коммутируемые конденсаторы пассивны по своей природе, они не усложняют проблему устойчивости активных фильтров.

7.3. Примеры реализации и использования активных фильтров

В этом параграфе приведем два примера активных фильтров которые были спроектированы в соответствии с техническими требованиями, обусловленными их промышленным применением. Цель анализа этих примеров состоит в том, чтобы показать, как можно использовать информацию, полученную в предыдущих главах, для создания удачной практической реализации. Эти примеры подчеркивают различные аспекты синтеза фильтров и призваны служить некоей направляющей линией.

В первом примере рассматривается ФНЧ, характеристика затухания которого приведена на рис, 7.3-1. Предварительно этот фильтр был реализован как пассивная цепь (см. рис. 7.3-2) и ус-

Затухание

70------

о-С

Частота, кГц

Рис. 7.3-1. Требования к характеристике затухания ФНЧ

1,0к0м

с,-. о,т5м9

Рис. 7.3-2. Реализация пассивного-фильтра, удовлетворяющего требованиям рис. 7.3-1

пешно использовался как один из элементов большой системы. Решение сделать эту систему гибридной привело к необходимости одновременно синтезировать активный фильтр для замены указанного пассивного.

Были реализованы и оценены три конструктивных варианта.

Вариант 1. Эллиптический фильтр пятого порядка с использованием ЧЗОС.

Вариант 2. Фильтр Чебышева седьмого порядка с использованием структурно-перекрытой реализации.

Вариант 3. Эллиптический фильтр пятого порядка с использованием каскадного соединения двух блоков второго порядка и одного блока первого порядка.

Из номограмм на рис. 2.2-5 и 2.3-5 следует, что любая эллиптическая функция пятого порядка с амплитудой пульсаций в полосе пропускания 0,18 дБ или функция Чебышева седьмого порядка с амплитудой пульсаций 0,1 дБ удовлетворяет техническим требованиям, приведенным на рис. 7.3-1. Для варианта 1, исполь-:зуя стандартную таблицу для аппроксимации эллиптических фильтров ,[80], получим пассивную цепь, схема которой показана :на рис. 7.3-3. Используя RLC-С/?1)-преобразование из § 6.2, получим схему, приведенную на рис. 7.3-4. Для нее при нулевой частоте найдем

y.JVBx=RBmA +Rb +4,48062).

Если положить 7?А = 100 Ом и приравнять (1) к 0,5, то полу-чим, что 7?в= 104,4062 Ом. Частотно-зависимое отрицательное сопротивление проектируется в предположении, что полные сопротивления на рис. 6.1-2,0 равны: Zi(s) = l/sC, Zzs) =R .Zz{s)=R,

i,B 1,шзб 2,от i,mio

о-I-1-r>rv-> , nnn , гуу-\.

о II I CZl-

Z,№ 1,20010

о,очт

o,iim

-1- вых

iPuc. 7.3-3. Реализация пассивного эллиптического фильтра. Зна-чения элементов даны в омах, генри, фарадах

Рис. 7.3-4. RLC-ОДД-преобразование фильтра, схема которого дана на рис. 7.3-3, с использованием ЧЗОС. Значения элементов даны в омах, фарадах, фарад-секундах

-Z4(s)=ii?4 и Z5(s) = l/sC. Следовательно, D = CRi. Выбирая С=1,0 Ф hR = 1 Ом, получаем, что значение Ri, которое требуется для реализации Dz, равно 1,30215 Ом. Аналогично, значение Ri, которое требуется для реализации Di, равно 1,21921 Ом. Нормированный :вариант схемы показан на рис. 7.3-5. Окончательная реализация получается путем частотного денормирования для частоты среза 17,5 кГц и денормирования полного сопротивления с коэффициентом 1000. Следовательно, окончательные значения элементов находятся путем умножения номиналов сопротивлений всех резисторов на 10, а номиналов емкостей конденсаторов на 9,0946-10-. Фактическая измеренная АЧХ полученной в результате схемы по-жазана на рис. 7.3-6. Заметим, что характеристики в полосе за-

держивания не удовлетворяют техническим требованиям. Последующими измерениями показано, что уровень полученного затухания фактически зависит от уровня входного сигнала; это говорит о наличии нелинейных эффектов, таких как ограничение скорости нарастания.

1,200(0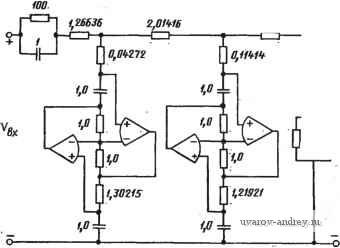

т. Увык

Рис. 7.3-5. Реализация фильтра, схема которого показана на рис. 7.3-4

Полученные ЧЗОС были испытаны по методике, аналогичной той, что была описана в § 6.2. Используя выражение (И) из того же параграфа, находим

Выбранные значения Ri и С дают следующие частоты излома характеристик: для D2 - 13,439 кГц и для D4 - 14,353 кГц. Необходимость измерения этих характеристик возникла, во-первых, потому, что нужно было снизить точку излома по причине, которая скоро станет очевидной. Чтобы сделать это, были использованы следующие значения: Ri = 107 кОм и С =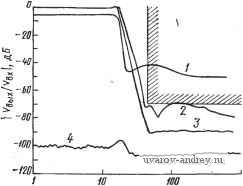

Рис. 7.3-6. Амплитудно-частотные характеристики, реализованные с помощью различных типов фильтров:

/ - фильтр на ЧЗОС (см. рис. 7.3-5); 2 - каскадная реализация (см. рнс. 7.3-П); -структурно-пере-

- ТП 9 сЬ Ятп пяпп тпиклг крытый фильтр (см. рис. 7.3-9); 4 - внутренний шум

- 1U . С?ТО дало точку в полосе Д/=10 Гц

15п<Р

излома на частоте 1467 Гц. На рис. 7.3-7 приведены результаты измерений. При этом выяснилась одна серьезная проблема, связанная с ЧЗОС-реализациями, а именно: выходное напряжение операционных усилителей растет с частотой, приводя к скачку в рабочем режиме, который вызывается ограничениями скорости нарастания выходного напряжения. На рисунке показаны две кривых для различных значений компенсирующей емкости Ср (использовался усилитель LM101A). Так как эффект скачка чувствителен

к амплитуде входного сигнала, то и характеристика фильтра чувствительна к уровню входного сигнала.

Из рис. 7.3-6 видно также, что отсутствуют нули в полосе задерживания для эллиптической функции. Из этого, очевидно, следует, что после-fKru, довательное соединение

¥ис. 7.3-7. Влияиие ограничений скорости на- Элементов ЧЗОСЩ не да-растания напряжения операционных усилите- ет резонансов . Исполь-лей на характеристики ЧЗОС зование операционных

усилителей, имеющих более высокую скорость нарастания выходного напряжения, позволило улучшить характеристику, но не настолько, чтобы удовлетворить техническим требованиям.

Для варианта 2 были использованы структурно перекрытая реализация и чебышевская аппроксимация. ФНЧ-прототип был взят :из обычных таблиц, его схема показана на рис. 7.3-184 При этом была выбрана односторонне нагруженная структура для того, чтобы исключить необходимость задавать сопротивление источника.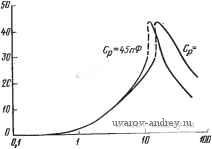

0,5т

1,6236 1,1981

Vex i.zmdp 1,1107- f,7j9s-L

1.0 П

-i-o

вб,Х

Рш. 7.3-Ь. Схема фильтра Чебышева

седьмого порядка. Значения элементов даны в омах, генри, фарадах

Структурно-перекрытая реализация этой цепи показана на рис. 7.3-9. Ниже приведены значения элементов схемы при полном сопротивлении 23,72 кОм и частоте среза 17,5 кГц:

/?=23,72 кОм, С1 = 226 пФ, С2=464 пФ, Сз = 623 пФ, С4=656 пФ, С5=690 пФ, Сб = 667 пФ, С7=565 пФ. В качестве инвертора используются операционные усилители LF156, а в качестве интеграторов - LM101. Амплитудно-частотная

Эта реализация была получена из табл. 13- работы flOl].

характеристика полученного фильтра дана на рис. 7.3-6. Очевидно, что структурно-перекрытый фильтр легко удовлетворяет техническим требованиям. Как показано на рисунке, затухание в полосе задерживания составляет -90 дБ. Это ограничение обусловлено, в основном, уровнем шумов фильтра, который довольно значителен

R ЧНп R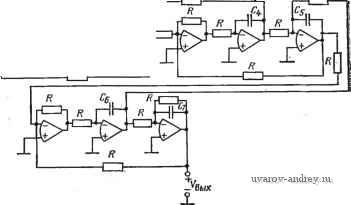

Рис. 7.3-9. Структурно-перенрытая реализация фильтра, схема которого дана на рис. 7.3-8. Интеграторы реализованы на операционных усилителях LMlOl,.

инверторы - на LF156

Второй каскад

2.6807

из-за большого числа операционных усилителей. Недостатком подобной реализации является то, что для нее требуется 10 операционных усилителей, семь прецизионных емкостей и резисторы 21-го-номинала. Большое число компонентов делает этот подход нежелательным для гибридизации.

Для варианта 3 было использовано каскадное соединение двух блоков второго порядка и одного блока первого порядка для реализации эллиптической функции. Чувствительность в этом случае не так хороша, как в первых двух вариантах, однако, так как число каскадов мало, результаты приемлемы. Положение нормированных полюсов для этого фильтра показано на рис. 7.3-10. Для блока второго порядка выбрана резонаторная схема, приве-

Первый, каскад .

[1-ри0507

DMI53

Рис. 7.3-10. Положение нормированных полюсов и нулей эллиптического фильтра пятого порядка

/0,6780

-jo,B7ea

-/1,0507

о)-/2,Ш7