го порядка, го для анализа такого режима нужно использовать аппарат теории импульсных систем [94]. В этом случае, как и в любой импульсной системе, полоса частот входного сигнала должна быть ограничена частотой /с/2.

То, что подход, использующий коммутируемый конденсатор, полезен, можно видеть, анализируя произведение 7?С-резистора и конденсатора. Если резистор замещается коммутируемым конденсатором, то Ri = TclCi. Следовательно, произведение RC или постоянная времени

Если используется МОП-технология, то коммутируемый конденсатор на рис. 7.2-\,а можно заменить схемой, показанной на рис. 7.2-2,а. Два полевых МОП-транзистора работают как ключи от двухфазного импульсного генератора, формирующего две непере-крытые импульсные последовательности (ф1 и фг) с частотой /с.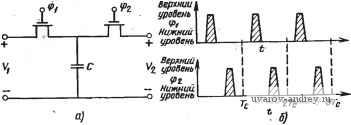

Рис. 7.2-2. Реализация коммутируемой емкости с помощью МОП-транзисторов

как показано на рис. 7.2-2,6. При подаче импульса ф1 конденсатор С подключается к напряжению Vi, при подаче импульса ф2 конденсатор С подключается к напряжению ¥2- В остальное время конденсатор С не подключен ни к ни к V2. Для данной частоты генератора значение тлс определяется отношением емкостей Так как конденсаторы Ci и С2 получают методами фотолитографии, то вполне достижима высокая точность отношения их емкостей. Можно показать, что ошибка при реализации такого отношения может быть меньше 0,1% при использовании стандартной МОП-технологии [95]. Так как такой МОП-конденсатор имеет характеристики, очень близкие к идеальным, то можно получить значительно большую стабильность и линейность, чем при использовании диффузионных резисторов. Кроме того, отношение емкостей, полученных по МОП-технологии, имеет очень слабую температурную зависимость. Из этого можно сделать вывод, что резистор на основе коммутируемого конденсатора (см. рис. 7.2-1,а) дает возможность изготовить высокоточный и стабильный 7?С-фильтр, который может быть целиком выполнен по интегральной МОП-технологии.

Основная схема, которая применяется во многих конфигурациях активных ?С-фильтров, представляет собой инвертирующий интегратор (рис. 7.2-3,а). Если резистор Ri в этой схеме заменить аналогом на основе коммутируемого конденсатора (см. рис. 7.2- 1,а), то в результате получим импульсный интегратор (рис. 7.2- 3,6). Когда ключ находится в позиции 1, Ci заряжается до напряжения Vrx. Если теперь перевести ключ в позицию 2, то заряд Ci

о-а о-

-о

Рис. 7.2-3. Схемы коммутируемого инвертирующего интегратора

передается конденсатору Сг, причем полностью, потому что операционный усилитель способствует тому, чтобы напряжение на конденсаторе Ci стало равным нулю. Полный заряд на Сг равен заряду, который был на Сг, до этого момента, минус заряд, который был передан на Сг конденсатор Сь .Этот заряд вычитается, так как рассматриваемая схема инвертирующая. В момент (п-1)Тс входной заряд на Ci

qi[(n-l)T,] = CiVRl{n-l)T,], , (3)

тогда как заряд на Сг

qA{n-l)T,] = Cv A{n-l)T,]. (4)

В момент времени пТс заряд qi[{n-1)Тс] передается на Сг, поэтому полный заряд на Сг становится равным

qAnT,)=-q,[{n-l)T,]-qA{n-l)Tj. (5)

Подставляя (3) и (4) в (5), получаем

вых (П Т,) - г^вых [( - 1) -(Ci/Q) V [(R- 1) rj. (6)

Преобразуя по Лапласу левую и правую часть равенства (6), имеем

VBMx (S) е^ ) = Fe.. (s)e< - c (С/С) v., (s) е^ -> с. (7)

Умножая обе части приведенного выше равенства на е- е, получаем

..-sT

Vsu (s) = VBMx (s) e-<-(CJC) F, (s) e

Множитель e-c соответствует ГВП Тс секунд. Решая относительно Увых{8)/Vbx, находим

вых (s) --{СМ е- с/(1 е-с) =

Ci/C,/(e-c i), (9)

Если sTcCl, то е с 1+sTc, и (9) принимает вид

Niis)V,u.(s) {-CjC)/sT,= -l/(s; C, . (10)

Передаточная функция обычного интегратора на рис. 7.2-3,а

(s) = ьых (*)/Vbx (s) = -1 /s RiC. (11)

Если s=jco, TO частотные характеристики (10) и (11) выражаются следующим образом:

Л/i (j (о) л; - 1 /j (О (Г jCi) Q = - сОо/j to; (12)

2(J) = -l/jto;?iQ=-tOo/jo), (13)

где (Оо - частота единичного усиления интегратора.

Следовательно, если oxl/Tc или /с*С2л, то на рис. 7.2-3,а аппроксимируется величиной Тс1С\ на рис. 7.2-3,6, и этот рисунок служит непосредственным эквивалентом, заменяющим рис. 7.2- 3,а. Интересно отметить, что постоянная времени интегратора может легко изменяться путем изменения частоты генератора импульсов.

Работу импульсного интегратора можно проиллюстрировать с помощью рис, 7.2-4. Предполагается, что входной сигнал синусоидальной с частотой /о, в 10 раз меньшей, чем частота генератора импульсов, а амплитуда импульсов равна 1 В. Выборка входного напряжения Fbx осуществляется в середине каждого интервала, равного периоду повторения импульсов, а ее значение Увх запоминается на конденсаторе Ci и сохраняется в течение полупериода повторения импульсов, пока, в соответствии с (5), не будет передано конденсатору Сг. Выходное напряжение сохраняется до тех пор, пока новая выборка не будет передана конденсатору Сг. В этом примере для синусоиды с частотой /о предполагается, что коэффициент усиления интегратора равен единице, как следует из (12), Поэтому (u(Tc/Ci)C2 в (12) равно единице, когда (u=(uo. Таким образом,

Ci/Ca = (о„ Гс = 2 я /о , = 2 я/10 = я/5. (14)

Согласно (6) только я/5 от входного напряжения вычитается из выходного. Если предположить, что fвых (0) = 1 В (выбрано произвольно), то можно вычислить Увых в момент Тс следующим образом. Ясно, что Vsx{TJ2) =sin 18°=0,309. Поэтому

ьых(7с) = ьых(0) -(я/5)г^вх(ВД= 1-0,194 = 0,806

Зту операцию можно повторить для получения выходного сигнала, вида рис. 7.2-4. Как правило, входная частота должна быть много меньше ,fc для того, чтобы уменьшить искажения выходного сигнала.

Многие из рассмотренных выше инвертирующих конфигураций, такие как резонаторная схема на рис. 5.2-4, требуют интегратора, который демпфирован, как показано на рис. 7.2-5,а. Передаточная функция этой схемы для Ni{s) -Увых() IVbx(s) имеет вид

л^1а )=(-ад1)/(и-] зС2). (15)

На рис. 7.2-5,6 дана импульсная эквивалентная схема, где ре-зисторы Rl и Rs, показанные на рис. 7.2-5,а, заменены на эквиваленты с коммутируемыми конденсаторами. Здесь важна фаза переключения ключей, которая указана стрелками. Стрелки означают следующее: ключи одновременно подсоединяются ко входу и выходу схемы, а затем одновременно подсоединяются к инвертирующему входу операционного усилителя. В момент времени (п- -1)Тс заряды на различных конденсаторах равны:

(7j( -l)T,] = Cit. [( -l)Tj; (16)

q, [( -1) Т,] = C,v, [( -1)Т,]; (17)

qs [(n-1) TJ = Сз W [( -1) П]. (18)

Тактовые импупьсы, коммутирующие переключатель в позицию 1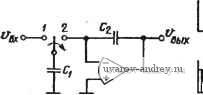

Тактовые импульсы, коммутирующие переключатель в позицию 2

О Та ZTcSTc Щ STc БГс ТГс вТс 9Тс Шс t

Частота Входной. ч синусоиды fnfrllO \ (m.e.To=fDTc)

0,2Щ----

! I

Cz fc 10 /

To t

Puc. 7.2-4. Диаграммы, поясняющие работу коммутируемого интегратора

в момент времени пТс ключи изменяют положение, что дает

ЯЛпТс) = Я2{{п-\)Т,\-я,[{п-\т-ЯЛ{п-\т. (19) Подставляя (16) - (18) в (19), получаем

-(Ci/C,)tBx[(n-l)7c]. (20)

=1=с, 4=£-

Vebix -о о-

а) S)

Рис. 7.2-5. Схема коммутируемого демпфированного интегратора

Переходя от временной области к области s и решаЯ'. относительно Л?2(5) =вых(5)/вх(5), получаем следующую передаточную функцию;

(S) (-Ci/C,)/(ec 1 + Сз/С,). Заменяя s на jico и полагая, что ecl+icoTc, находим, (j (0) - (СгЮ (TJCM1 + j (Tc/Q Cs],

где <оТс<1. Из (15) и (22) ясно, что Ri = TcfCi и /?з=Гс/Сз.

Схема другого основного компонента активных JC-фильтров- дифференциального интегратора показана на рис. 7.2-6,а. Диф-

(21) (22)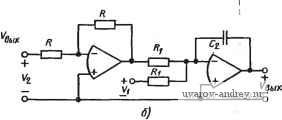

fuc. 7.2-6. Схема коммутируемого дифферен-здиального иНгегратора

ференциальный интегратор позволяет провести интегрирование разности двух сигналов. Аналоговая реализация дифференциального интегратора приведена на рис. 7.2-6,6. Анализ этой схемы дает

1вых (s) - -K/S) [Vi is)-V, (s)], (23)

где ft)o=l ?iC2. Хотя каждый резистор на рис. 7.2-6,6 мог бы быть заменен эквивалентными на основе коммутируемых емкостей, более эффективна импульсная реализация, приведенная на рис. 7.2-6,е. Используя ту же процедуру анализа, можно выразить VBbix(s) на рис. 7.2-6,е в виде

вых (S) - [Vi.(S)- (s)]/s (TjCd C, (24)

где для s=jft), юГс-С!.

Коммутируемые конденсаторы для замены резисторов достаточно просто применить в активных /?С-цепях. И здесь, хотя каждый резистор можно заменить непосредственно эквивалентом с коммутируемым конденсатором, более эффективна замена функциональных узлов, таких как на рис. 7.2-6,6, с помощью схем на рис. 7.2-6,е.

Рассмотрим, например, резонаторный фильтр, показанный на рис. 7.2-Т,а. Это та же схема, что и на рис. 5.2-4, за исключени-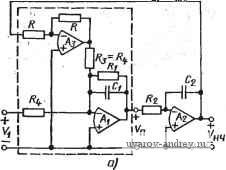

Рис. 7.2-7. Схема коммутируемого резонаторного фильтра

ем того, что Rs=R4. Передаточные функции нижних частот и полосовую можно найти из (19) и (20) (см. § 5.2):

- s/Rs Cj

Vi (s) 5== + s/RiCi+l/Rz Rs Ci Cjj (s) XlRRCiC

Vi (s) + slRiCi-\-\/RRs Ci Q

(25) (26)

Ограничение, вводимое требованием Rs=R4, состоит в том, что коэффициент усиления на частоте Юп ФНЧ-реализации будет равен 1. Можно показать, что комбинация схем на рис. 7.2-5,6 и рис. 7.2-6,е позволит реализовать часть схемы, обведенную пунктиром на рис. 7.2-7,а. Если для оставшегося инвертирующего интегра-

тора используется схема на рис. 7.2-3,6, то в итоге получаем схему аналогового фильтра с выборкой данных, которая приведена на рис. 7.2-7,6. Конденсаторы, которые являются эквивалентами резисторов, помечены штрихами и имеют индексы, соответствующие резистору, который они заменяют. Передаточную функцию схемы на рис. 7.2-7,6 можно найти, если применить те же приемы, что и выше, к соответствующим компонентам этого рисунка. Например, передаточная функция схемы, обведенной пунктиром, может быть записана в виде

Vn . НЧ (s)-Vx (27)

\+s Tc(CdC\)

если для s = j(D (оГс-С!. Сочетая эти результаты с полученными для инвертирующего интегратора, находим

s- LYfs + ,-£L L + . Ly (28) TcCi] \ nCi Tl Ci

Vi(s)

Передаточная функция нижних частот

V (s)

s + s--L + -L.] .(29) Ге Cl Tl c, cl

Пример 7.2-1. Аналоговый резонаторный фильтр с выборкой данных. Требуется спроектировать .резонаторные ФНЧ и полосовой фильтр второго порядка, имеющие Q=20 и fn= 1 кГц, используя выборку данных. Частота генератора импульсов должна быть равна 100 кГц. Обозначим отношение емкостей конденсаторов следующим образом: ai=Ci/Ci и ОгСУСг. Принимая в (29), что С'1=С'2=С'з, получаем

102 = 4 7-2; OianTc/Q. (30). (31)

Из техничеошх требований .получаем: ai=0,00314 и 02=1,256. ♦

Из выражения (30) и приведенного выше примера ясно, что произведение aia2 должно быть равно 4nf\fPc, а принимая, что значения а близки к единице, получаем, что частота генератора должна быть в 40 раз больше частоты полюса фильтра. По мере того, как частота фильтрации приближается к частоте тактового генератора, оказывается необходимым дополнительный анализ фильтра с использованием г-преобразования [94]. Различие между аналоговым фильтром и фильтром с выборкой данных показано на рис. 7.2-8 (используются данные предыдущего примера). Как только частота приближается к fc, частотная характеристика последнего вновь идет вверх вместо того, чтобы снижаться до нуля, когда fooo, как это происходит в аналоговом фильтре. Это явление называется эффектом наложения. Возможно, окажется необходимым дополнительный аналоговый фильтр, включаемый каскадно с фильтром с выборкой данных, для того чтобы скорректировать этот эффект. Если fnfc, то дополнительный фильтр е общем случае не обязателен.

Другой важный момент заключаетсяв том, чтобы избежать задержки на полтакта. Например, согласно рис. 7.2-7,6, когда Vii изменяется в некоторый момент времени и принимает новое значение, оно поддерживается постоянным в течение полного периода тактового генератора. Ключ, коммутирующий конденсатор Сг, можно сфазировать так, чтобы выборка нового значения Уц происходила либо сразу, как только оно появится, либо спустя полтакта. Можно показать [96], что если выборка происходит спустя полтакта, то избыточное запаздывание по фазе появляется, когда не выполняется условие fn-C/c- Поэтому было бы хорошо сфазировать ключи так, чтобы выходное напряжение интегратора передавалось в последующую цепь сразу же, как только произошло его. изменение.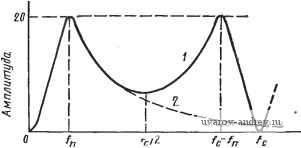

/с/2 Частота

Рис. 7.2-8. Эффе1{т изложения в коммутируемых фильтрах: 1 - коммутируемый аналоговый фильтр; 2 - аналоговый фильтр

Чувствительность фильтра с выборкой данных должна быть такой же, как в случае эквивалентного ему аналогового фильтра, пока fn не начнет приближаться к fc. Чтобы исследовать чувствительность изменений а к fn{!c, необходимо избегать предположения, что ecl+sTc. Для анализа этой проблемы проводится преобразование s-плоскости в г-плоскость. Оно имеет вид

zeo (32)

Следовательно, обратное преобразование г- = е~ с должно соответствовать задержке в Тс секунд. Возвращаясь к выражению (9), видим, что инвертирующий интегратор, использованный на рис. 7.2-7,а, можно охарактеризовать соотношением

-CiCz

-2 /

l-z-

Передаточную функцию обведенной пунктиром части рис. 7.2-7, можно выразить как

схемы на

-l-H Ci/Ci

[1/,(8)-Унч'( )].

(34)

Преобразуя это выражение из s-плоскости в г-плоскость, получаем

Уп() =-1УАг)-Упч()]. (35)

z-l + C[/Ci

Объединяя (33) и (35), находим

-(з/С.)(г-1) 3g

Viiz) г^- {2-C[/Ci)z+ll+{CyCi){CyC2)-C[/Ci]

Биражение (36) можно упростить, подставив Сз=С'1 и использовав соотношения ai = Ci/Ci и а2=С 2/С'2. В результате получим

(2) i(г) = - 1 (г- l)/[2-(2-ai) г + (1 -f а^а^-а^)]. (37)

Умножая (87) на (33), можно получить передаточную функцию нижних частот

Унч (г)/У1 (г) =--. (38)

Тогда положение пары комплексно-сопряженных полюсов в s-плоскости можно записать в виде

si.2 = -tOn/2 Q ± j (cOn/2 Q) VWl. (39)

В г-плоскости положение этих же полюсов определяется выражением

гь 2 = Reekie (40)

Подставляя (39) в (32) и сравнивая полученное с (40), получаем следующие формулы:

f = {fj2n)V+WT Q=-2xfjf,lnR. (41).(42)

Типовой знаменатель второго порядка при наличии пары комплексно-сопряженных полюсов в г-плоскости можно представить в виде

D (г) = (z-z) iz-z) = iz-R cos G-j R sin G) {z-R cos G -f

+ ji?sinG) = e-2/?cosGz-b/?2. (43)

Соотношения (41) - (43) позволяют получить более точные по сравнению с (30) и (31) расчетные формулы для ai и а2, когда <е=с^1-1-5Гс. Сравнивая знаменатель (37) или (38) с (43), находим

а, = 2{1 -e- n/fcQcos[(я/J/J VA-i]]} ; (44)

a,= l-b(l/ai)(e- W i). (45)

Подставляя значения, использованные в примере 7.2-1, в эти формулы, получаем ai = 0,00708 и 02 = 0,5567. Эти значения отличаются от найденных в примере множителем, примерно равным 2. Если частота тактового генератора увеличивается до 1 МГц (или

частота fn уменьшается до 100 Гц), то значения ai и аг, полученные из (30) и (31), становятся равными соответственно 0,00031416 И 0,1256, тогда как (44) и (45) дают 0,0035356 и 0,11607 соответственно. Следовательно, даже если частота фильтрации много меньше частоты тактового генератора, некоторые реализации, такие как реализация на рис. 7.2-7,6, становятся, очевидно, очень чувствительными к изменению отношения fnlfc-

Чувствительность к ai и аг можно определить из (44) и (45), предполагая, что Q l и fn<fc. Тогда находим

1 fn

sin

2jt/ V f,

Sn =-1--1! Q.

:0; Sl2nfMc.

(46)

(47)

(48),(49)

Как только fnlfc становится много меньше 1, чувствительность fn к Oi приближается к 1/2. С другой стороны, чувствительность Q к аг может стать большой (при большом Q), если отношение fnlfc будет приближаться к 1. Это означает, что fnlfc должно быть мало, чтобы сохранить низкую чувствительность при больших Q.

Схемы с выборкой данных могут быть также использованы для реализации фильтров на основе переменных состояния. Один из путей осуществления этого показан на рис. 7.2-9. Заметим, что

\С5 Се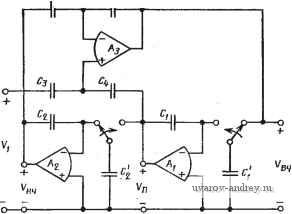

Рис. 7.2-9. Схема коммутируемого фильтра, реализованного по методу переменных состояния

замена резисторов Rz, Ri, Rs и Re (см. рис. 5.2-2) коммутируемыми конденсаторами не изменяет идеальной передаточной функции суммирующего дифференциального усилителя. Замена Ri и .г коммутируемыми конденсаторами приводит к схеме на рис. 7.2-9.