ствующего НЧ-ВЧ-преобразования) ФВЧ с частотой среза 10 кГц. На частоте среза значение (от(сй) приблизительно равно 3,3л. Если используются полистироловые конденсаторы, то по данным табл. 3.8-2 имеем; Qc=5000. Используя в (3) Qh как Ql, получаем Да=0,029 дБ. Это означает, что отклонение от функции а (со) на частоте 10 кГц будет равно 0,032 дБ. Если эта реализация используется для синтеза ФВЧ с частотой среза 20 кГц, то Ql становится равной 313 и отклонение затухания, рассчитанное с помощью (3), Да=0,153 дБ.

Анализ, аналогичный приведенному выше, можно провести и для методов моделирования, в которых используются ЧЗОС или КОИ. Для ЧЗОС, реализованных с помощью ЦОИ, пригодна модель операционного усилителя, представленная на рис. 6.7 - 9. Однако, когда такая модель используется в эквивалентной схеме, то вычисления добротности Q становятся значительно сложнее, часто для этого приходится использовать программу машинного анализа цепей [81]. Модель операционного усилителя, пригодная для использования в такой программе, приведена на рис. 6.8-2.

Рис. 6.8-2.- Модель операционного усилителя, пригодная для использования . в иро^праммах машинного анализа цепей

Аналогичная ситуация возникает, когда требуются КОИ, используемые как двухполюсники. Другие случаи применения КОИ (например, параллельно-каскадный метод) не допускают такого использования. В этих случаях частотная характеристика реализации обычно ограничена неидеальностью входных полных сопротивлений в результате того, что в таких схемах входные зажимы, усилителя не заземлены. До настоящего времени, однако, в литературе не появилось исчерпывающего анализа частотной характеристики для такого случая-

Последний метод синтеза путем моделирования пассивных цепей, который здесь рассматривается, - метод структурно-перекрытой реализации. Он также может быть проанализирован с использованием (3). Чтобы показать, как это делается, вспомним, что этот метод требует, чтобы функции входных иммитансов былц реализованы как передаточные функции по напряжению активных цепей. Если обычную передаточную функцию по напряжению обог

значить как A(s), а входную функцию (предположим, полного сопротивления) через Z(s), то указанный метод требует, чтобы

Л(s) = dzl/Z(s), (4>

причем А (s) инвертируется, если в (4) стоит знак минус, и не инвертируется, если имеется знак плюс. Фаза Z(jcu)

arg [Z (j со)] = arctg {Im [Z (j cu)yRe [j со)]} = arctg Q, (5)

где Q - добротность полного сопротивления. Однако, так как на практике Q обычно велико, выражение (5) можно записать в виде

arg[Z(jcu)] jt/2-1/Q. (6>

На основании (4), предполагая, что знак положителен, можно записать

arg [А (j со)! = -arg [Z (j )] -п/2+ 1/Q, (7)-

а для знака минус

arg [А а со)] = я-arg [Z (j со)J я/2 -f 1 /Q. (8)

Аналогичные соотношения получаются, если указанный иммитанс представляет собой полную проводимость. Выбор знаков плюс или минус либо полного сопротивления или проводимости осуществляется в зависимости от особенностей метода (см. § 6.3). Например, для реализаций ФНЧ все внутренние лестничные входные иммитансы имеют вид l/Fs, т. е. представляют собой индуктивности или емкости. Следовательно, все передаточные функции по напряжению будут реализовываться неинвертирующими или инвертирующими интеграторами.

Чтобы проиллюстрировать этот метод, рассмотрим рис. 6.3-8,а\. на котором представлен структурно-перекрытый эквивалент пас-сийного двусторонне нагруженного ФНЧ пятого порядка, показанного на рис. 6.3-5,а. Видно, что в структурно-перекрытой схеме индуктивности моделируются неинвертирующими интеграторами, состоящими из каскадного соединения инвертора и инвертирующего интегратора. Такой каскад аналогичен показанному на рис, 5.4-9 и анализируется в § 5.4. Аналогично вышеприведенному можно видеть, что емкости моделируются инвертирующими интеграторами типа показанных,на рис. 5.4-1. Фазовый сдвиг инвертирующего интегратора находится из (7), § 5.4,

arg [А (j со) ] я/2 + сй;?с/сй Лр-co/GB. (9>

Объединяя это выражение с (8) [для знака минус в выражении' (4)], получаем

Qc = 1/Ыс/(иАо~(й/ОВ) -GB/(o, (Щ-

где Qc - соответствующая добротность смоделированной емкости... Знак минус исцользуется для того, чтобы показать, что в схеме-существует запаздывание по фазе. Qc является добротностью всех смоделированных емкостей в реализации. Запаздывание по фазе неинвертирующего интегратора дается выражением (24), § 5.4,

; arg [Л (] ] .-я/2-3©/GC. (11>

Используя (7) и (11), получаем добротность смоделированной индуктивности

Qi -еВ/Зсо. (12)

Добротности, полученные в (10) и (12), можно использовать в (3) для получения отклонения затухания для фильтра на основе структурно-перекрытой реализации:

Да л; 4,34 (-4 со/СБ) сот (ю). (13)

Приведем пример использования этого соотношения: если для реализации фильтрующей функции, приведенной на рис. 6.в-I, применяется схема, показанная на рис. 6.3-8,а, то для частоты среза

Да(сй) 180--дБ. (14)

Следовательно, если предположить, что ш/05 = 0,01, то Да= =-1,8 дБ, что является, конечно, значительным отклонением. Эту характеристику структурно-перекрытой реализации, показанной на рис. 6.3-8,а, можно улучшить путем более тщательного проектирования интеграторов. Например, если для инвертирующего интегратора используется схема на рис. 5.4-8, то из (21), § 5.4, получаем

Qc I/:(oj/GBi-co/GBa + CHBjc/GBi GB-atjc/AoiJ-GBjGB/aMiiic

(15)

Аналогично, если для неинвертирующего интегратора Используется схема на рис. 5.4-10, то из (28), § 5.4, получаем

qlGB/a. (16)

Из обоих приведенных выше выражений следует, что добротности имеют противоположные знаки, что приведет к уменьшению Аа(сй). Полагая GB = GB2=GB и (о=сйдс, можно упростить (15):

Qc-(GBM\ . (.17)

Подставляя (16) и (17) в (3), получаем

Да ((о) 4,34 1(й/0В-{а/0В)Ц сот (ю). (18)

1Если со - частота среза, то (18) принимает вид

Да (&)45 ((n/GB) (1 - co/GB). (19)

Сравнивая это выражение с предыдущим и полагая (u/GB = =0,01, находим, что Да=0,446 дБ. Таким образом, почти в 4 раза [уменьшается отклонение функции затухания, что наглядно показы-:вает нелосредственное влияние, которое оказывает выбор схемы :интегратора на характеристики результирующей реализации.

Аналогичный анализ можно провести и тогда, когда методы структурно-перекрытой реализаций используются для реализации ПФ, в этом случае величины Ql й Qc являются добротностями (бЛоков второго порядка. Следовательно, анализ должен быть со-

средоточен на добротности этих цепей. Полученную в результате добротность можно подставить в (3), чтобы определить характеристики реализации.

6.9. Выводы

В этой и предыдущих главах было дано введение в методьЕ синтеза активных /?С-фильтров. В гл. 4 и 5 было показано, как можно синтезировать звенья второго порядка /?С-фильтров на усилителях и каскадно соединять эти звенья для получения фильтров высокого порядка. В этой главе, однако, использовались существенно отличные методы синтеза. В ней был сделан упор на непосредственную реализацию фильтра в целом (вне зависимости от его порядка), а не на реализацию отдельных звеньев второго порядка функции фильтрации цепи. Методы, представленные в этой главе, можно разделить на две группы. Первая группа оперирует непосредственной реализацией пассивной цепи-прототипа. В этой: группе первые два метода, а именно, использующие искусственную индуктивность (§6.1) и ЧЗОС, обеспечивают непосредственное моделирование элементов цепи-прототипа. Метод искусственной индуктивности особенно хорошо приспособлен для реализации ФВЧ, тогда как метод, использующий ЧЗОС, непосредственно применим для реализации ФНЧ и ПФ. В § 6.3 представлен еще один метод - структурно-перекрытой реализации. Применяемый в нем подход существенно отличается от предыдущих. Для НЧ реализаций в нем используются интеграторы в качестве функциональных узлов в активных /?С-структурах, которые моделируют переменные состояний (ток и напряжение) цепи-прототипа^ В этомг случае интеграторы заменяются полосовыми функциональными узлами второго порядка на /?С-усилителях, рассмотренными в гл. 4-и 5.

Вторая группа методов, представленных в этой главе, использует в качестве исходной фактически желаемую функцию цепи, а не пассивную цепь-прототип. Первый из этой группы методов - метод использования ОРБ (см. § 6.4), в котором подобно методу структурно-перекрытой реализации используются в качестве функциональных узлов звенья второго порядка. Второй метод в этой группе - параллельно-каскадный метод (см. § 6.5). В нем также используется непосредственно функция цепи, но применяются КОИ; и пассивные цепи.

Уместно привести некоторые общие соображения, касающиеся; этих двух различных путей, используемых в методах синтеза, описанных выше, для определения желаемых характеристик фильтра а именно, использование пассивной цепи-прототипа и функции цепи. В общем случае более удовлетворительные результаты получаются при использовании цепи-прототипа, так как соответствующая техника денормирования позволяет найти значения элементов: получаемой в итоге активной реализации без заметной потери точности, С другой стороны, использование в качестве исходной точки

Шнтеза функции цепи, а также значений ее к'оэ!)фициентов для численного задания технических треббвний являётЪя; по суЩёстку, менее точной процедурой. Причина этого заключаете в т6м, что каждый такой коэффициент представляет собой результат операций, проведенных над численными значениями нескольких элементов цепи.

.л

и , ; . . 1. i:

.:6-г7- 1 (§ 6.1). а) Найдите параметры передачи для реаиизации иа апераци' онных. усилителях .ИНУТ, схема которого показана HaVpric- 3.6-Iio. Считай-: Tej.;4T0 операцианный усилитель идеальный, т.. .е. имеет бесконечно большой коэфф-ициент усиления, нулевое выходное и бесконечно--большое входнйе полные сошротивлек'ия. б) Повторите задачу для реализации ИТУН на рис. 3.6-1,6. i в.) Повторите задачу для реализации ИТУТ, показанной на рис. 3.6-1,в.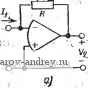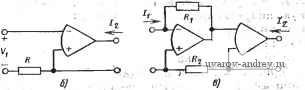

Рис. 3. 6-1

..... .. . \\:

.16-2 (§ 6.1), 1) Получите выражения для параметров передачи,.шриве--денныхВ (4), § 6..1. , ..

б) Повторите, задачу для параметров, приведенных ,Bi i.(.5:), § 6.1. . i:.::. 6-3 {§ 6.1),а) Найдите параметры передачи для четырехполюсника, показанного иа рис. 6.1-2, копда выходная пара зажцмов йвределяется Ka.i4 ла-.;р.а зажимов, где присоединяется 2i(s). Предполагается, что Zi{s) не-Я1Вляется частью четырехполюсника. ,; : ,

,б) Повторите задачу для Zz{s).

-..:в) Повторите задачу для 2з(5). , i:,.,

6-4 (§ 6.1)., а) Реализуйте полное сопротивлеше Zbx(.s)sK, используя ЩрИ схема которой -дана на рис. 6.1-2 и только, однп резист,оры и конденсаторы для полных сопротивлений .Zi-(s)-Z6(s,). Ес,ли;:-нрм-инал с01против.ления -резистора равен 1 кОм, а номинал емкости конденсатора .1 -мкФ, чему будет iPSBBa постоянная-К? Определите ее размерность. .

6j Повторите задачу для полного сопротивления,Zb.x{-s) =№

в) Повторите задачу для полного сопротивления,Zb-t(s) f=,-Ks2. :!,::

, 1г) Повторите задачу для полного сопротивления.2bx:(s) =№^-

..д) Повторите задачу для полного сопротивления Zbxi(s)=jK/s3. 1 , . . 6-5 (§ 6.1). Полагая, что диапазон - возможного изменения номинадоэ.:сопротивлений составляет от 1 до 100 кОм, а номиналов емкостей от 100 пФ;.до 1 , мкФ, найдите диапазон возможных значений иокусств,енной индуктивности, з<оторый может быть, реализован,.,едли 1испрл1>з<?э,а^ 6.Л.-2,..

6-6 (§ 6.1). а) Найдите., ф.ункрш! цепи, F<n(s)/l/i(s), и Vm{s).iViis) для ЦОИ' иа .рис. 6.1-3 для случая, когда Z2(s)=l/sC и Jii=iRs=JiiiRi=R-Примите С=0,1 мкф и R=10 кОм. Начертите диаграмму Боде для. модулу, каждой из передаточных функций. , ,

б) Повторите задачу для случая, где. рее полные сопротивления представляют собой резисторы с номиналом R, да цскдючением Zi{s) = lisC.

6-7.{§ 6.1). ,Иопользуя .метод и,скусртвенной индуктивности, синтезируйте односторонне нагруженный ФВЧ четвертого порядка, реализующий баттервор-товскую передаточную функцию по напряжению. Сопротивление нагрузки должно быть равно 1000 Ом, а частота среза - 500 Гц. Фильтр-прототип можно найти, иопользуя таблицы в приложении А. Используемая для .реализации искусственной индуктивности ЦОИ должна иметь Z2(s)=l/sC. Сопротивления искусственной индуктивности должны им!еть равные номиналы--10 кОм.

6-8 (§ 6.2). а) Для цепи а рис; 3.6-8,а найдите передаточную функцию по напряжению для разомкнутой цепи V2{s)IVi(s) и обозначьте положение полюсов и нулей. Будет ли лередато1ная функция в устойчивой?

6) Повторите задачу для цепи на рис. 3. 6-8,6.

Рис. 3:6-8

6-9 (§ 6.2). Номиналы сопротивлений и емкостей в схеме на рис. 6.2-2 лежат IB пределах от 1 до 100 кОм и от 100 пФ до 1 мкФ соответственно. Каков диапазон изменений постоянной D, определенной в (1), § 6.2?

6-10 (§ 6.2). Получите выражения, показывающие, в каком соотношении находятся значения ненормированной постоянной D ЧЗОС, определенной в (1), § 6.2, и нормированной постоянной £) , используя постоянные денормирования-. по частоте и сопротивлению, т. е. Qn и z , определенные в § 1.4.

6-11 {§ 6.2). Используя ЧЗОС, синтезируйте фильтр, реализующий передаточную функцию Баттерворта нижних частот четвертого порядка. Частота среза должна быть равна 5 кГц, сопротивления источника и нагрузки прототипа должны быть paiBHbi 500 Ом. Фильтр-прототип можио найти из приложения А. Все резисторы ЧЗОС должны иметь сопротивления 7500 Ом. Полученная в результате реализация должна иметь цепи, связывающие по постоянному току все входы операционного усилителя с землей.

6-12 (§ 6.2) .С помощью ЧЗОС синтезируйте реализацию характеристик: затухания, показанных на рис. 3.6-12. Для аппроксимации этих характеристик, используйте эллиптическую функцию третьего порядка. Фильтр-прототип можио синтезировать, используя приложение А. Денормируйте полное сопротивление реализации с коэффициентом 10*. Все конденсаторы ЧЗОС должны иметь, емкости 10-* Ф. Полученная в результате реализация должна иметь цепи, связывающие по постоянному току все входы операционных усилителей с землей.

6-13 (§ 6.3). а) Если первые элементы лестничной цепи являются шунтирующими, а возбуждение на вход подается от источника постоянного тока

то какой вид будет иметь эквивалентная схема, соответствующая схеме на .рнс. 6.3-3, которая моделирует указанную цепь? Пометьте иапряженяя И полярность для каждого иммитансного блока.

б) Повторите задачу, используя схему, показанную на рис. 6.3-4.

6-14 {§ 6.3). а) Начиная со схемы на рис. 6.3-5,6, сформируйте общую жонфигурацию фильтра, токазанного на рис. 6.3-9,а.

б) Повторите задачу для конфигурации, показанной иа рис. 6.3-9,6.

5Г

/ г 3

f,Kru,

Рис. 3. 6-12

6-15 (§ 6.3). Используя метод структурно-перекрытой реализации синтезируйте фильтр, имеющий передаточную функцию Баттерворта нижних частот пятого порядка. Частота среза должна быть равна 1 крад/с. Сопротивления нагрузки должны быть одинаковы и равны 10 кОм.

6-16 (§ 6.3). Выведите выражение (10), § 6.3, исходя из схемы, показанной на рис. 6.3-12. Считайте, что операционные усилители идеальны,

6-17 6.3). Синтезируйте ПФ Чебышева шестого порядка с передаточной функцией, имеющей среднюю частоту 1000 Гц и ширину полосы, рав-гаую октаве с амплитудой пульсаций 1 дБ. Конденсатор должен иметь емкость 10 * Ф. Сопротивления, нагружающие фильтр, должны быть одинаковы и равны 1000 Ом. Используйте резонаторную схему на рис. 6.3-12 для реализации блоков второго порядка.

6-18 (§ 6.3). а) Получите таблицу, подобную табл. 6.3-1; покажите при этом, как реализация универсального активного фильтра на рис. 5.3-1 может быть попользована для реализации полосовых блоков второ'го порядка, требуемых в методе структурноперекрытой реализации. В частности, указанная выше реаливация должна давать значения Ru R2, Rs, Ri и R, выраженные через значения элементов на рис. 6.3-11,а.

б) Повторите задачу для значений элементов на рис. 6.3-11,6.

6-19 (§ 6.4). Используя метод ОРБ, синтезируйте фильтр, имеющий те .же технические требования, что и в задаче 6-17, лричем Н=\. Используйте р'ис. 6.3-12 для реализации блоков второго лорядка.

6-20 {§ 6.4). Используя метод ОРБ, синтезируйте ПФ Баттерворта десятого порядка, передаточная функция которого имеет среднюю частоту и ширину полосы 2000я рад/с. Синтезируемая структура должна иметь вид, аналогичный локазанному на рис. 6.4-2, т. е. процедура синтеза должна дать характеристики блоков второго (Порядка и значения сопротивлений резисторов об-гратиой связи. Сопротивление резистора Ro должно быть выбрано равным 10 КОм.

и 12,5*10 12,010

11,0x10 <>]0,5*101-

-j2,0*10f

6-21 (§ 6.5). Используйте параллельно^каскадный метод для того, чтобы п-олучить реализацию следующей нормированной передаточной функции:

V2 (S) iVx (S) = (s - + 2s- 1) /(s8 + 2s2 + 2s + 1)

Денормируйте реализацию, используя значения fi =Zn = 103 для постоянных денормирования, определенных в § АА. В искомой реализации примите-/-,i=rgi = 10 кОм и C2i=CH=Ci. Найдите значение d для КОИ.

6-22 (§ 6.5). Иопользуя параллельно-каскадный метод, синтезируйте фильтр, имеющий передаточную функцию Баттерворта нижних частот четвертого порядка с частотой среза 6,28 крад/с. Используйте постоянную денормирования по сопротивлению z = = 10 кОм. Примите /ii=3i= 10 кОм и C2i = C4t=-Ci. Определите значения Ci для каждого КОИ.

6-23 (§ 6.5). Используя параллельно-каскадный метод, синтезируйте передаточную функцию по напряжению, полюсы и нули которой показаны иа рис. 3.6.23. Используйте постоянную денормирования по сопротивлению Z =10 кОм. Примите Ги = ГЗг = \ кОм и C2i = C4i =

= Ci. Определите значение Сг для каждого КОИ.

6--24 (§ 6.6). Начертите график, похожий на тот, что показан на рис. 6.6-3, для элементов 7?i, кг и С4 ЧЗОС-реализации примера 6.6-1 (см. рис. 6.6-2,6).

6-25 (§ 6.6). Найдите величину d/(jl) / W{jl) для ЧЗОС-реализацин примера 6.6-1, которая получится Б результате изменения сопротивлений всех резисторов в схеме на +10%.

6-26 (§ 6.6). Найдите величину dJV{j2) /Л/(]-2) для схемы искусственной индуктивности примера 6.6-2 при изменении температуры на 30°. Считайте, что все конденсаторы имеют температурный коэффициент -1-250 -/° С> а все резисторы температурный коэффициент -500-Ю-/ С.

6-27 (§ 6.6). Проведите сравнение чувствительностей пассивных односторонне и двусторонне нагруженных фильтров Баттерворта нижних частот третьего порядка. Чтобы сделать это, вычертите графики Sx для элементов фильтра, схема которого дана на рис. 6.6-6, и сравните их с графиками, полученными в прнм-ере 6.6-1 и задаче 6-24. Покажите, что в последнем случае графики те же, что и графики для пассивного односторонне нагруженного фильтра.

6-28 (§ 6.6). Найдите чувствительности 1Л?(]ю) к и Сц односторонне нагруженного фильтра Баттерворта нижних ча1СТот третьего порядка, синтезированного по методу структурно-перекрытой реализации. Сравните результаты при <о = 1 с теми, что были получены в примере 6.6-3.

6-29 (§ 6.7). Покажите справедливость выражения (Г), § 6.7.

6-30 (§ 6.7). Реализуйте искусственную индуктивность, считая, что У4{5) на рис. 6.7-1 представляет собой конденсатор, а все другие элементы резисторы. Используя методику, изложенную в § 6.7, покажите, может ли Q((u) быть независима от GE\ и СВг и если да, то какие соотношения обеспечивают этот результат?

6-31 (§ €.7). Повторите пример 6.7-1 для случая, когда GBi=A,\ МГц, а Gfi2=l МГц.

Рис. 3. 6-23

6-32 (i§ 6.7). Получите соотношение, аиалогичное (25) в § 6.7, для случая, когда ЧЗОС .реализуется путем выбора Zi(s)=J?i, Z2(s)=i?2, 2з{$)=1/зСз, Zi(s)=Ri, 2s(s)=il7sCs. Определите, может ли Q(<a) быть не зависима от GBi и GB2, если да, то какие соотношения обеспечивают этот результат?

6-33 {§ 6.7). Полагая, что в ЧЗОС-.реализации G2=G4=Gs=G и Ci = =Сз=С, начертите график Qц^QQ (w) для а) GB,>GB2, б) GBi = CB2 и б) GBi<gB2- Положите ,4о1=Ло2=Ло.

6-34 (§ 6.8). а) Найдите отклонение зату.хания Да на частоте среза од-йосторонне нагруженного фильтра Баттерворта седьмого порядка, реализованного с помощью .пассивных элементов. Считайте, что конденсаторы полистироловые и добротности катушек индуктивности равны 100.

б) Повторите задачу для катушки индуктивности с добротностью 30.

6-35 (§ 6.8). Найдите минимальную добротность катушки индуктивности .для фильтра, описаниого в задаче 6-34, -если максимальное значение Ла должно быть 0,5 дБ на частоте среза.

6-36 (§ 6.8). Начертите график зависимости Да (со) в дпалазоне частот от. О до 1,2 рад/с для фильтра Чебышева нижних частот пятого порядка с амплитудой пульсаций 1 дБ, реализованного на пассивных элементах. Используйте ..графики группового времени прохождения, приведенные на рис. 6.8-1. Считайте, что все конденсаторы майларовые, а добротности катушек индуктивности постоянны' и равйы 100, т. е. не зависят от частоты.

. 6-37 (§ 6.8). Найдите Да на частоте среза структурно-перекрытого фильтра примера 6.3-1, реализованного схемой на рис. 6.3-10,6. Считайте, что операционные усилители имеют GB = 1 МГц.

6-38 (§ 6.8). Найдите отклонение затухания Да на частоте среза для фильтра Баттерворта нижних частот четвертого порядка, реализованного по методу ЧЗОС. Предположите, что высокочастотная добротность ЧЗОС, проанализированного НО методу, аналогичному ошисанньим в § 6.7, равна 500 на Частоте среза. Считайте, что Qc=oo, так как емкости реализуются резисторами.

6-39 (§ 6.8). а) Используя модель операционного усилителя, приведеы-ную на рис. 6.8-2, и соответствующую программу машинного анализа [81], получите АЧХ для частот от О до 2fc для реализации, приведенной в задаче 6-38. Используйте следующие параметры операционного усилителя: Ri = = 104 Ом, Rn=Rp=°°, Ci=0, Ло=105 и Ro=m Ом.

б) Повторите задачу для случая, когда Rn и Rp изменяются до значения 500 МОм, а .со = 10 рад/с.

ЗАКЛЮЧЕНИЕ

В этой главе обобщим наши представления об активных фильтрах, рассмотрев два заключительных вопроса. Первый из них - перспективные направления исследования фильтров. Среди многих возможных задач, которые следовало бы проанализировать, вы-

браны только две, возникшие в настоящее время, но имеющие большое будущее. Одна из них - разработка фильтров для ВЧ диапазона. Этой задаче посвящен § 7.1, где исследуются активные /?-фильтры, т. е. фильтры, не использующие емкостей. Вторая за- дача связана с аналоговыми фильтрами с выборкой данных, известными также как фильтры с комтлутируемой емкостью. Этот тип фильтров является особенно удобным для интегральной МОП-технологии. Он описан в § 7.2.

Второй важный вопрос в области активных фильтров - процесс синтеза. В § 7.3 подробно описан процесс синтеза активного фильтра, удовлетворяющего техническим требованиям промышленного применения. Обсуждаются преимущества и недостатки различных типов фильтров, изученных в предыдущих главах.

7.1. Фильтры в области высоких частот

В этом параграфе рассмотрим реализацию ВЧ фильтров. Верхняя граница частотного диапазона активных фильтров равна примерно 10... 20 кГц для большинства технических решений, которые мы исследовали. Основная причина этого ограничения заключается в конечном значении произведения GB операционных усилителей, используемых в реализациях. Влияние ограниченного значения GB сводится к тому, что полюсы фильтра сдвигаются по отношению к желаемым позициям. В некоторых реализациях этот сдвиг может в конечном счете привести к неустойчивости. С ростом требуемой добротности реализации частотные ограничения, вызванные конечным значением GB, становятся все более серьезными. Выше были рассмотрены методы, исключающие влияние GB на передаточную функцию (см. §5.7); эти методы предполагают согласование между усилителями. На практике, однако, типичное значение согласования GB внутри выборки операционных усилителей, таких как 1д,А747, может составлять ±5%. Следовательно, если они не будут настроены более точно, использование методов § 5.7 позволит расширить полосу рабочих частот примерно до 100 кГц. Однако на практике и 100-килогерцовый диапазон трудно достижим, если учесть влияние ограничений на скорость нарастания выходного сигнала. Чтобы реализовать такую высокочастотную характеристику, скорость нарастания операционного усилителя должна быть максимально возможной, а амплитуды сигналов усилителей должны быть ограничены низкими уровнями.

Проведенное рассмотрение показывает, что частотный диапазон порядка 100 кГц для активных фильтров может быть достигнут, если используются техника компенсации или более высокочастотные операционные усилители. В этом параграфе изучим различные подходы к реализации высокочастотной характеристики, а именно, применение специальных методов синтеза, которые позволят расширить частотный диапазон.

Прежде чем продолжить обсуждение, было бы уместно спросить, является ли такой результат желаемым. В самом деле, для