Если GB2Gb = GB\GA, то Q(co) примет вид

Qo(co).

со (G, + Gs)/ Gs Gs] + (I /со) [G (G4 + Gs)/ G4]

где Qo(co) определяется как Q(co) для Zbx(J(o) выражения (7) с тем ограничением, что операционные усилители согласованы и что GiGb. Итак, при учете неидеальности усилителя зависимостью первого порядка влияние того, что произведение коэффициента усиления на ширину полосы операционного усилителя конечно, устраняется при симметричной схеме искусственной индуктивности. Следовательно, Qo(co) представляет собой предел Q для искусственной индуктивности при согласованных усилителях. Если предположить, что Ао1=Ло2=>1о, Gi = Gz = Gi = Gt,= G и Y2(s)=sC, то (14) упрощается, принимая вид

Qo И = 1/(2/Ло) (со/соо + соо/со), (15)

где (ito=\IRC. Отсюда следует, что Со(ю) максимальна и равна Ао/4 на частоте со=соо, которая соответствует максимально достижимой добротности Q этой схемы. Например, если 40=10, то Qo(coo) =25 ООО. Это значение достигается только при со=соо и будет уменьшаться для любой другой частоты, как показано на рис. 6.7-4.

WuJg

Рис. 6.7-. Зависимость добротно- Рис. 6.7-5. Зависимость добротности от частоты для модели индук- сти от частоты для модели катушки тивности, реализованной с помощью индуктивности, реализованной с по-согласованных операционных усилн- мощью несогласованных операцион-тслей ных усилителей:

а - GB, > GB2, б - GB, = GB2; в -

GBi<GB2

Рассмотрим теперь поведение Q(co), определенной (13), для случая, когда усилители не согласованы, т. е. когда их произведения коэффициента усиления на ширину полосы различны. Если вычертим график Q(cuo), т. е. зависимость Q(cu) для переменной величины 1Сй==сйс, то найдем, что существуют три варианта в зависимости от соотношения GBi и GB2. Они показаны на рис. 6.7-5. Полагая, что GiGs, если GBi = GB2, можно свести (13) к (14), а Q(coo) для каждого значения соо просто к Ло/4. Этот случай соответствует прямой б на рис. 6.7-5. С другой стороны, если GBi>GB2, то разность l/GBz-l/GBi будет всегда положи-

тельна, а реакция будет похожа на ту, что представлена кривой а на рис. 6.7-5. Наконец, когда GBi<GB2, то разность I/GB2- -\/GBi будет отрицательна. Это приведет к тому, что Q((0o) становится бесконечно большой при некотором значении ш. Следовательно, даже при больших значениях юо схема на рис. 6.7-3 будет неустойчивой до тех пор, пока сопротивление возбуждающего источника на входе достаточно велико. Типичный график для этого случая соответствует кривой в на рис. 6.7-5. В следующих ниже примерах будет показано, что для кривой в максимальное значение Q((o) может стать больше, чем максимальное значение Q((0o).

Пример 6.7-1. Добротность искусственной индуктивности. Требуется начертить график IQ (со) I для реализации с помощью ЦОИ искусственной индуктивности, в которой используются усилители с oi=.i4o2=10 GBi = l МГц, СВ2=1,1 МГц и CDo=10 рад/с. Из (13) получаем

Q (со) = Ао/12 (oj/cDo + соо/со)-0,01818 со].

Решая относительно частоты, при которой Q(co) = oo, находим со=1054рад/с. Следовательно, график Q(co) имеет вид, показанный на рис. 6.7-6. ф

oj, pad/c

Puc. 6.7-6. Зависимость добротности от частоты для модели индуктивностч, реализованной в примере 6.7-1

Добротность Q(cu) используется для того, чтобы характеризовать свойства искусственной индуктивности. В идеальном случае наиболее желательно получить кривую вида б рис. 6.7-5. Получение такой характеристики вполне реально, так как произведения GB монолитных операционных усилителей, изготовленных на одном и том же кристалле, как это наблюдается на практике, хорошо согласуются и имеют почти совпадающие температурные зависимости. Следовательно, прекрасные характеристики искусственной индуктивности легко получить на практике, положив Ri=R5 и используя согласованные операционные усилители.

Другой случай формирования искусственной индуктивности, когда Y4=sCi, дает аналогичные результаты.

Рассмотрим теперь другой активный элемент цепи, реализованный на ЦОИ, - ЧЗОС. Его можно анализировать аналогичным способом. Если элементы ЦОИ выбрать так: Yi(s)=sCi, Y2{s) = G2, Уз(5)=8Сз, Y4s) = G4 и Y5(s) = G5, то (1) можно записать в виде

у^ (S) = S Gi s Q + GBi (s + Wg) s Сз (g4 + Gb) + GB (s + cogi) X

GBi gb2 g2 g4 + GBi (s + (Oaz) s c3 (g4 + g5) + GBs (s + co) G X

XGs (g4+g5) + (s+COoi) (S+C0 2) (g4+g5)

X (g4 + g5) + (s + таг) (s + co 2)(g4+c5) Исключая члены, которые не содержат GBt и GB2, получаем

(16)

ех

sGi

[GBi Сз (g4 + g5)] + (GBi GB2 Сз g5) s -kg4 + Съ) GB2 Gz cOg, [GBi Сз (g4 + g5)] s2 + [(g4 + g5) (GBi ma2 Cs + GBGz)] s +

+ GBi G£2 G2 g4

Выделяя множитель, соответствующий полной проводимости идеального ЧЗОС и деля числитель и знаменатель на произведение GBiGBz, имеем

GvG,

G4 + с5 J (G4 + G5) G2 COfli 1

GbGBs CsGbGBi s

Сз (g4 + Gb) g g4 + g5 / coa2 c3 Ga

g2g4gb2 g2g4 \ GB2 GBi j

.(18>

Находим обратную величину, принимая s=J(o и полагая, что

(oCAG, + G)/GB GG,<:l; получаем входное полное сопротивление ЧЗОС

4х (j =

l+jco

g4 + (g4 + Gs) с3 C0q2

g4gb1

Go g4 GBo

co= Cl Сз Gs

l + Jco

g4 + g5

(g4+g5)G3C0a,

c3 g5 GBj

(20>

[g5gb2 .

Так как идеальный ЧЗОС имеет фазовый сдвиг, равный п рад то Re[zbx(jcu)] -отрицательна и много больше, чем Im[zi)x(j(b)]-Следовательно, фазовый сдвиг (20) можно аппроксимировать выражением

arg (J со)] п + 1т [Z (j co)]/Re [Z (j со)]. (21)/

Тогда добротность ЧЗОС

Q430cH = Re[ZB,(j )]/Im[Z (jco)]. (22)

Эта. величина, представляет собой меру близости характеристик ЧЗОС идеальным, а именно:, фазовому сдвигу 180° и АЧХ вида \G2GM<oCiC3Gs\. . .....

Из (21) и (22) получаем

Q430C М 1 /(arg [2вх (j fi>)] -1)-

Из (20) находим arg [Zb (j (о)] = я + arctg (о G4 + G5

G4 + C5 L G4GB1

(С4 + О5)СзС0аа G2G4GB2

-arctg со

G5GB2

(G4 + G5)G2Cua

(24)

Если (o<zGB, то, используя этот результат в (23), имеем

Q430C ( ) = 1 /{ (G4 + G5) [ 1 /G4 GBi-1 /G, СБа] +

+ (G4 + Gs) (со C3/G2 G, + G,A4oi со Q G]}. (25)

Сравнивая (25) для ЧЗОС с (13) для искусственной индуктивности, можно заметить, что за исключением индексов оба выражения для добротности идентичны. Следовательно, если GBiG4= = GB2Gb, то ВЧ характеристика добротности ЧЗОС Счзос(о>) будет независима от произведения GB операционных усилителей. Для согласованных усилителей значение Q430C (<и) в НЧ области должна иметь максимум Ло/4, если Ло1=Ло2=Л, G2=Gi=Gs=G и Gi = C3=C. Это максимальное значение Q430C наблюдается при <йо=G/C. При другом выборе емкостных реактансов, отличных от Zi(s) и Z3(s), получим аналогичные характеристики. Примеры, подтверждающие это, можно найти в задачах. Подытоживая полученные выше результаты, видим, что независимость свойств ЦОИ от произведения GB усилителя делает привлекательным ее применение при реализации искусственных индуктивностей и ЧЗОС.

Кроме указанных, в § 6.1 был введен еще один активный элемент - КОИ. Он использовался в методах реализации ЧЗОС-фильтров, а также в параллельно-каскадной реализации. Один из методов анализа КОИ состоит в вычислении его постоянной /(c(s), определенной в (1), § 6.5. На рис. 6.7-7 показана схема, удобная

Рис. 6.7-7. Схема КОИ на операционных усилителях, не имеющих бесконечно большего коэф-, фициента усиления

4 С

для таких расчетов. Используя анализ по методу контурных токов, находим

. /, (S) Zi г, + jZi Z, + ZiZs) Aai ,

his) Z2Z,(AdiAd2 + Adi+l)-{-ZsZi(l+Ad,)-

...Бели, как и в (1), § 6.5, определим

Kc{s) = (sRiR3CC,)E{s),

где E{s)-сомножитель, который учитывает неидеальность поведения К.ОИ, тогда применяя подход, аналогичный использованному для искусственной индуктивности и ЧЗОС, можно показать, что

arg [Е (j со)] я-(cui?3QMoi + 1Л4о2 со С^). (28)

Если Ло1==Ло2=Ло и &о=1ЩзС2, то (28) примет вид

arg [Е (j со)] зх-(1Мо) (co/coo-f сйо/(о). (29)

При получении этого результата была учтена та особенность, что упрощение произошло благодаря вычитанию членов, содержащих произведения GB обоих операционных усилителей. На практике эти результаты могут, конечно, отличаться от приведенных из-за конкретных характеристик полного сопротивления нагрузки 2б(5) на рис. 6.1-2,а. В общем случае, однако, можно ожидать, что характеристики, реализованные КОИ, аналогичны характеристикам, реализованным искусственной индуктивностью и ЧЗОС. Следовательно, все эти схемы полезны для реализации активных фильтров высокого класса.

Можно также проанализировать эти схемы в режиме большого сигнала. Такой анализ достаточно утомителен из-за сложностей, возникающих в результате наличия как положительных, так и отрицательных обратных связей в этих схемах. Как таковой, он выходит за рамки данной книги.

Так как влияние произведения ОБ усилителей можно исключить в большинстве рассмотренных применений, включая КОИ и ЦОИ, то важно проанализировать механизм, который действительно ограничивает частотные возможности этих цепей. Покажем это на примере, используя искусственную индуктивность. Прежде чем сделать это, рассмотрим ЦОИ на рис. 6.7-1, где Yi{s)=sC/t и Yi(s) = llRi (j=l,2, 3, 5), как показано на рис. 6.7 - 8. Схема за-

Рис. 6.7-8. Реализация искусственной индуктивн-ости с помощью ЦОИ

Рис. 6.7-9. Схема замещения операционного усилителя, использованною в схеме на рис. 6.7-8

мещения операционного усилителя, которая используется при такой анализе, показана на рис. 6.7-9. Она содержит входное и выходное сопротивления, а также сопротивление в режиме синфазного сигнала. Используя эту модель в схеме на рис. 6.7-8 и проводя упрощения в предположении, что R\=R2=Ri=Rb=R и С\=С,

получаем в результате эквивалентную схему, показанную на рис. 6.7-10. При анализе этой схемы было показано [77, 78], что она эквивалентна схеме на рис. 6.7-11, причем имеются следующие соответствия:

R[ (2 R+3Rb)+GBRC 2R,

R (2R+3R +GBR Q

R 2 + GBRC \Ri Cpfil/GBR) (2 +ад); = 2 R/Aa + 3 RJAo + RVRc ;

Ro R

(30a) (306)

(ЗОг) (ЗОд)

L = i? С ; Lp = 2 R/GB + 3 RJGB, (ЗОж), (ЗОз)

гле Ru=Ri2==Ri, Roi=Ro2=Ro, Ло1=Ло2=Ло, GBGBGB, и Rc - параллельное сопротивление конденсатора С. Если значения

1. %1 +М м fnz JU pz

X-1-t

rvSr-k l

Рыс. 6.7-10. Схема а рис. 6.7-8 при использовании схемы замещения на рис. 6.7-9

Рис. 6.7-11. Эквивалентная схема цепи на рис. 6.710

полного сопротивления операционного усилителя соответствуют идеальным Rc=оо, то

Gpi = 2/RAo; Gps{2lR){<s>IGBf\ rp = 2RU\; LRC;

Gp2 = 0; Cp л; 2/RGB; rp, = 2Ricu/GBf: Lp = 2RlGB.

(31a), (316) (3lB),(31r) (31д),(31е) (31ж),(31з)

Удобно разделить эту модель на две эквивалентные схемы: одну для области нижних частот, другую для области верхних частот. Для области нижних частот находим, что ГрГрь, Gpi или Gp2Gp3 и cuCp<l/(cuLp-bcu-o). Следовательно, входную полную проводимость можно записать в виде

унч (j со) = Gpi + Gp2 + I /[7-Р4 + i со (L + Z-p)] = Gi, + I /j , (32)

где . . =

Gl =Gpi + Gp2+W[%4 + (o + pn; (33)

V% +0) (Lo + LpfV( {Lo+Lp) I 4-Lp (34)

И-где предполагалось, что Гр4сй(.о+Ьр). Тогда добротность искусственной индуктивности на низких частотах

= - Im [Кнч (j )yie [унч (j )] = 1 /со G, = = cu(Lo + Lp)/{(Gp,-fGp,)[r2,-fcu(L -fLp)]+rpJ. (35)

Так как Gpi>0 и G,p2<l0, то Ql может быть положительной или отрицательной, в зависимости от относительных значений параметров операционного усилителя. В' любом из этих случаев модуль велик, так как Gpi, Gp2 и Гр4 - очень малые величины. Qi, можно сделать положительной путем увеличения Gpi, что эквива-.яентно включению шунтирующего сопротивления на входе искусственной индуктивности. На высоких частотах, где ГрГр и Gp3>-Gpi или I Gp2. можно записать следующее выражение для входной полной проводимости искусственной индуктивности:

У^Ц()-Сн+ l/jcuLH = Gp3-f jcuCp+ I/[rp5 + jcu(L + Lp)], (36)

Gh = Gp3 + гр,/[г1 + co (L + ЬрГ] (37)

. . L = ° + - + --- . : (38)

. . (Lo + Lp) - Cp[r% + aiLo + Lpr]

Тогда добротность Q искусственной индуктивности на высоких частотах можно представить в виде

... .. т - .[вх(i[УТ(j )] - (о+Lp)/{Gp,[j-i, +. .

+ (Ц1, + 1рГ] + Гр,}, (39)

где предполагается, что rp5<i(ii(i-o + Lp) и Ср&{Ьо+Ьр)<с1-

Выражения для добротностей Ql и Qh, приведенные выше, слишком сложны, чтобы можно было сделать какие-то о.бобвдения. .Можмо, однако, показать, что характеристики искусственной индуктивности зависят не только от произведения ОБ и Ао, но и от уровней полных сопротивлений усилителя. Это влияние показано яа рис. 6.7-12, где процентное отклонение индуктивности от Jo рассмотрено как функция частоты для различных значений Lo при пбстоянном R и для различных значений R при постоянном Эти данные приведены для операционного усилителя 741 ..имеющего следующие параметры: Лр = 2-10 GB= 1,2 МГц, ?о = 75Ом, Яг =2-.10Ом, Rp=Rn = 50D МОм. Из рисунка ясно, что существенное 0Т]Клрнение, индуктивности наблюдается при частотах выше 10 кГц. Компенсации эффектов, показанных на рис. 6.7-12, можно достичь добавлением конденсатора Сс (пунктир на рис. 6.7-8) . П,)йцент11ое отклонениеиндук-гивности для различных значений

приведено на рис. 6.7-13. На этом рисунке использованы-зна--~;п,..ч параметров операционного усилителя р,Л741, указанные в!Ы-ше; кроме того; Z,o = 0,088 Гн и R=2 кОм. Следовательно, используя такую технику компенсации рабочего частотного дианйэойй активного элемента, можно расширить его по крайней мере до 20 кГц. , - .....V .. Л;:,. .;. 1 .4

1 10

Частота, кГи,

0,1 I 10 Ш

Частота, кГц

Рис. 6.7-12. Влияние паразитных параметров усилителей на характерист.чки

искусственной индуктивности

I IS

ё -10

Следует заметить, что результаты, полученные в этом параграфе и относящиеся к характеристикам ЦОИ- и КОИ-реализаций, должны быть модифициров^аны, когда полные сопротивления опст рационных усилителей неидеальны. Это особенно верно, учитывая особые свойства произведения GB- Причиной влияния полного сопротивления на ЦОИ- и КОРЬ реализации является то, что в этих реализациях ни один из входных зажи.мов операционных усилителей не заземленпо Сигналу. Если бы один из этих за>кимов был заземлен, то уровень' полного сопротивления в этой точке был бы соответствующим уровнем кажущейся зём-Лии, следовательно, неидеаль-нйй вход и полное сопротивление в режиме сийфазного сиг-

нала имели бы незначительное частвта,к:Гц

(ши вообще не имели бы) вли- ,

Рис. 6.7-13. Использование компенси-

яние на указанную реализа- рущ^ е^ улучшения харак-

ЦИЮ. Очевидно, .-.что. такие ; pea- теристик. иокуоственнодшщдукттаноети

ШпЯ>

лизации активных фильтров, как структурно-перекрытые, в которых операционные усилители не имеют заземленных зажимов, пред-полтнтельнее благодаря своей возможности обеспечить хорошие характеристики в области высоких частот..

6.8. Частотно-зависимая чувствительность

В § 4.7 и 5.6 было введено понятие частотно-зависимой чувствительности. Эта чувствительность была введена для того, чтобы установить соответствие между положением полюсов ?С-фильтра иа усилителях и произведением GB операционных усилителей, использованных при реализации. В этом параграфе распространим это понятие на фильтры, реализованные по методу моделирования пассивной цепи, рассмотренному в предыдущих параграфах этой главы. В таких фильтрах, учитьтая, что порядок реализованных функций достаточно высок, более удобно рассмотреть чувствительность функции цепи, а не чувствительность полюсов. Такой вывод согласуется с аналогичным выводом, полученным при рассмотрении чувствительности в § 6.6.

Чтобы начать анализ частотно-зависимой чувствительности для фильтров, основанных на моделировании пассивных цепей, рассмотрим сначала цепь-прототип, в которой последовательный резистор с сопротивлением Ri имеется для каждой катушки индуктивности Li, а шунтирующий резистор с проводимостью G, имеется для каждого конденсатора С,. Кроме того, потребуем, чтобы для всех значений i и /.

Li/Ri = QL; Ci/GiQc. (1)

Про такую цепь говорят, что она имеет квазиоднородные поте-ри*. Характеристики чувствительности такой цепи для случая, когда она имеет вид резистивно нагруженной лестничной цепи, были исследованы Блостейном [79]. Он исследовал функцию затухания а((о), определенную в (5), § 3.2, и показал, что отклонение затухания Да(сй) можно выразить следующим образом:

Ла (со) = 4,34 {{\IQl + 1 IQc ) сот (оз) + 0,5 (1 IQl - 1 IQc ) 1ш (р^ + р,)], (2)

где т(сй) -функция группового времени прохождения, а pi и рг - члены, характеризующие мощность, отраженную от оконечных элементов цепи. Мультипликативная KOHCTaHTa (множитель 4,34), вводится для того, чтобы изменить единицы измерения затухания ( о), т. е. перейти от неперов к децибелам. В большинстве фильтров первый член в правой части выружения (2) является доминирующим для значений со в полосах пропускания и переходной (между полосой пропускания и полосой задерживания). В этих областях т(сй) обычно велико. Следовательно, для этих частот (2) может быть упрошено:

Да 4,34 (1/Ql+I /Qc ) сот (со). (3)

Если Ql = Qc, то говорят, что цепь имеет однородные потери.

Это уравнение, хотя оно было выведено для ограниченного класса фильтров, очень важно при оценке методов моделирования пассивных цепей. Трудность его применения связана в основном с трудностью получения выражения функции группового времени прохождения т(сй), так как она должна быть вычислена на основе определения, данного в (30), § 2.5. Ее можно получить и из справочников или других литературных источников для стандартных фильтрующих функций [80]. Для приближенного анализа ее можно принять постоянной в полосе пропускания. Например, для нормированного по частоте (ширина полосы I рад/с) ФНЧ Баттерворта -Г0 порядка удобной аппроксимацией будет т(ю) секунд.

Рассмотрим теперь применение (3) к различным методам моделирования пассивной цепи. Рассмотрим сначала метод, который использует КОИ и ЦОИ. Здесь можно применить выражение (39), § 6.7, для высокочастотной добротности Qh смоделированной индуктивности. Пусть операционный усилитель [хЛ/741 имеет следующие параметры: Ло=2-105, GB = 1,2 МГц, Ro = 7b Ом, Ri = 2 МОм и Rr = 500 МОм'. Для ЦОИ, полагая, что сопротивление резистора, параллельного конденсатору С, т. е. Rc, равно 100 МОм, а также что R = 2 кОм и С=22 нФ, находим, что Qh 2292 на частоте 10 кГц. На 20 кГц соответственно С2нЛ::313. Следовательно, Q для смоделированной индуктивности резко уменьшается с возрастанием частоты, ограничивая при этом частотную характеристику реализации. Влияние добротности Q на передаточную функцию можно исследовать с помощью выражения (3). Рассмотрим в качестве примера рис. 6.8 - 1, на котором показаны функции затухания

Рис. 6.8-1. Характеристики затухания (а) и ГВП (т) для чебышевской фувкиуш нижних частот пятого порядка с амплитудой пульсации 1 дБ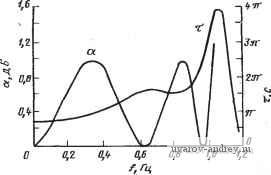

И группового времени прохождения для функции фильтрации Чебышева нижних частот пятого порядка с амплитудой пульсаций 1 дБ. Предположим, что реализация этой функции должна быть использована как схема-прототип для реализации (после соответ-

Rp и -входные сопротивления для синфазного сигнала положительного и отрицательного входов операционного усилителя, как показано на рнс. 6.7-9.