


 |
 |
 |
|
Главная страница » Электрика в театре » Фильтрация и сравнение активных и пассивных лс фильтров изучения 1 2 3 4 5 6 ... 38 T(s) через произведение N{s)N{-s) и использованием в качестве полюсов N{s) полюсов функции T{s), лежащих в левой полуплоскости, и половины любых пар полюсов четного порядка той же функции, лежащих на оси jo, а в качестве нулей N{s) -нулей функции T{s), лежащих либо в левой, либо в правой полуплоскости, и половины любых нулей четного порядка, лежащих на оси jo. Ограничение на использование лишь тех полюсов T{s), -которые лежат в левой полуплоскости, введено только из соображений устойчивости. Ниже рассмотрен соответствующий пример. Пример 2.1-1. Нахождение функции цепи по заданной АЧХ. Как при-мер, .подтверждающий справедливость сказанного выше, рассмотрим функцию /V(jtu)2=((B2+l)/((B*+l). (5) Легко видеть, что связанная с ней функция Т (s2) = + 1)/(5* + 1) = (S-Ь 1) ( -S-j- l)/(s + V2s + 1) (s -Л/2з + 1). Сравнивая (6) с (4), видим, что существуют две функции цепи N(s), удовлетворяющие (5): Ni = {s+ l)/(s2 +-\/2s+1)hN is) = (s- l)/(s2 + yUTs + 1), (7) причем в выражении для Nzis) знак в числителе изменен на противоположный, так как это не влияет на квадрат модуля Л'(]ш) р. ♦ Необходимые и достаточные условия, полученные выше для функции квадрата модуля, в общем случае можно легко применить к определенным конкретным характеристикам фильтров. Рассмотрим, например, определение функции квадрата модуля, характеристика которой в низкочастотной области начинается с нулевой частоты и является максимально плоской. Один из путей получения максимально плоской характеристики - добиться того, чтобы как можно больше производных такой функции были равны нулю при (й = 0 рад/с. Такая функция называется максимально плоской. Чтобы уяснить, как это может быть сделано, запишем обобщенное выражение функции квадрата модуля A(jco) в следующем виде: \N{ia)\ = HЦl+ba + ba + ...)/(l+aa + aa+...). (8) Если теперь разделить знаменатель на числитель, то получим liV (i (о)2 = Я2 [1 + (&i-ai) io + {b~a, + a\-ab,) (о*+...]. (9) Рассмотрим теперь ряд Маклорена, т. е. разложение в ряд Фурье в начале координат произвольной функции Р{а)). Оно имеет вид где F> (0) - i-я производная F выражение с разложением для о) в точке ш = 0. Сравнивая это ЫЦа)], данными в (9), и пере- писывая его так, чтобы оно было идентично с полученным разлд- жением, можно заметить, что в силу четности iA/(jco)p все его производные нечетного порядка равны нулю. В дополнение к требованию равенства нулю второй производной потребуем, чтобы были равны коэффициенты Ui и &i. Аналогично этому, наряду с требованием равенства нулю четвертой производной, будем требовать равенства коэффициентов аг и &2 и т. д. Таким образом, обобщенная максимально плоская функция квадрата модуля Л^(]ш) заданная (8), характеризуется следующим ограничением, накладываемым на максимально возможное число коэффициентов: at = h. (И) В качестве применения этого критерия, рассмотрим функцию квадрата модуля для цепи нижних частот. Такая функция имеет плоскую характеристику на низких частотах и спадает до очень малых значений на высоких частотах. Таким образом, идеально можно было бы представить себе, что такая характеристика выглядит так, как показано на рис. 2.1 1. Однако характеристика, приведенная на этом рисунке, не реализуема. Более практичный подход при нахождении функции цепи нижних частот - постараться аппроксимировать такую характеристику путем выбора функции квадрата модуля Л/(]ш)Р, которая была бы максимально плоской при со = 0. Это должно привести к воспроизведенпю плоской формы кривой, по крайней мере, в области нижних частот. С другой стороны, чтобы обеспечить необхо-димый спад характеристики в области верх- с; них частот, необходимо расположить все ну- -ли передачи искомой функции в бесконечности; следовательно, числитель Л/(jco) должен быть просто константой и все коэффи- р^ 2 /-Идеальная циенты Ьг в (8) должны быть равны нулю. характеристика ФНЧ Для максимально плоской характеристики с учетом (11) коэффициенты at должны быть также приравнены нулю, за исключением, конечно, старшего. Результирующая функция квадрата модуля A(jC0)2 = 2/(l-f 8(02 ), (12) где Н - величина (0), т. е: максимальная величина, которой достигает A(jtu); е используется для того, чтобы регулировать скорость убывания амплитуды. Некоторые значения е и приведены в табл. 2.1-1. Диапазон частот Ocol рад/с называется полосой пропускания этой функции, а диапазон частот ш>-1 рад/с Общим необходимым и достаточным условием реализуемости является сг<а<оо,где критерий Пэлн-Винера, который требует, чтобы j -о Л^(](в) -исследуемая на реализуемость АЧХ. 1-f и' называется полосой задерживания. Следует заметить, что при ш = 1 рад/с модуль \N{\\)\=Н1{\+-г^у1, причем эта величина не зависит от п. Значение е обычно выбирается равным единице, тогда такая функция именуется функцией Баттерворта^. В этом случае модуль \N(il)\=Hi 1/2 = 0,707Ш и 20 lg[ A(jl) /iV(0) ] ] = =20 Ig 0,7071 =-3,01 дБ; таким образом, за частоту 1 рад/с обычно принимают частоту на уровне - 3 дБ или частоту спада на 3 дБ. Из (12) следует, что наклон функции квадрата модуля Л^(]со) р на этой частоте пропорционален - п/2. Графики АЧХ функции Баттерворта для п=2, 5 и 10 показаны на рис. 2.1-2. Значения амплитуды в некоторых точках характеристики Л'(]со) приведены в табл. 2.1-2. Для до-0,5 1,0 1,5 2,0 статочно больших значений час- , . тоты ослабление составляет Рис. 2./-2. Амплитудно-частотные ха- р, npKanv пп шкале ча-рактеристики функций Баттерворта Д^> на декаду по шкале ча различных порядков стот выше 1 рад/с. Здесь п - сте- пень данной функции. Местоположение полюсов функции цепи, имеющей характеристики Баттерворта, можно найти, используя (4) и (12). В результате получаем  N{s)N{-s)-- (13) 1 + 1) Приравнивая полином в знаменателе нулю, находим, что полюсы располагаются в точках s, удовлетворяющих соотношению s=[-(-1) ]1/2п. (14) Следовательно, для п четных s=(-\yp- = Qinhi2n (,= 3, 5,... ... ,4n 1), для п нечетных s= (1)2=ginft/2 i (у^О, 2, 4,..., 4 -2), Из этих соотношений видно, что полюсы N{s)N{-s) расположены на окружности единичного радиуса на одинаковом угловом расстоянии друг от друга, как показано на рис. 2.1 -3. Рассматривая только левую полуплоскость, находим, что полюсы -V(s) определяются как pk=Ok + ](i)h, где Ofc=-sin-n; to = cos3x, k= I, 2, 3,..., п. (15) Такое оцределение полосы за1Держивания справедливо, строго говоря, только для идеальной АЧХ, для реальной АЧХ полоса задерживания начинается с частоты, затухание на которой .больше или равно заданному. Между полосой пропускания и полосой задерживания лежит переходная полоса. Этот факт не упоМИнается авторами и ниже рассматриваются только две полосы: пропускания и задерживания. - Прим. пер. Баттерворт был британским инженером, который описал этот тип частотной характеристики шримекительио к электронным усилителям в статье К теории избирательных усилителей , см. [1, с. 536-541]. Десять лет спустя Лэндон применил термин максимально плоский в своей статье Усилительные Каскады с максимально плоской характеристикой , см. [2].
Примечание. А - амплитуда. Полиномы В знаменателе, имеющие такие корни, называются полиномами Баттерворта. В табл. 2.1 -3 приведены коэффициенты полиномов Баттерворта, координаты полюсов и не равный еди-
а) б) в) Рис. 2.1-2. Корни полиномов Баттерворта нице коэффициент квадратичного множителя для различных значений п. Реализация баттервортовских функций пассивными цепями приведена в приложении А. Соотношение (12) может использоваться для определения значения п, т. е. порядка фильтра, необходимого для того, чтобы удовлетворить заданным требованиям в процессе проектирования. Пример 2.1-2. Определение порядка функции Баттерворта. Рассмотри!* определение функции цепи нижних частот, имеющей максимально плоскую АЧХ со спадом на 3 дБ от максимального значения (который она имеет на нулевой частоте) на частоте среза полосы пропускания 10 = 1 рад/с. Кроме этого, требуется, чтобы АЧХ имела спад на 15 дБ на всех частотах выше 0= =2 рад/с. Вследствие монотонности максимально плоской характеристики, удовлетворив второму требованию на частоте со = 2 рад/с, тем самым удовлетворим ему и на более высоких частотах. Заметим, прежде всего, что наличие Затухания точно -15 дБ на частоте со=2 рад/с соответствует требованию, чтобы 201g[yV(jO)l/.A(i2)] = 15, что, в свою очередь, приводит к требова- Значения амплитуды максимально плоской (баттервортовской) функции (е=1) с нормированной полосой пропускания (и=1 рад/с)
Таблица 2.1-36 Положение полюсов и квадратичные множители (s+fliS+l) максимально плоской (баттервортовской) функции с полосой пропускания О... 1 рад/с
Замечание. Все функции нечетного порядка имеют также полюс в точке s=-l. нням, чтобы lgAf(jO)/.W(j2) 1=0,75 и yV(jO) I/iyV(j2) 1 =5,623. Таким образом, необходимо удовлетворить неравенству l/V(jO)/iyV(j2) = (1 + 22 )/2 5,623. (16) Оно может быть представлено в виде ft > (1/2) loga [(5,623)2 - 1] = log2 5,53. (17) Так как log2 последовательности чисел. 2, 4, 8, 16, 32, ... имеет соответственно значения I, 2, 3, 4, 5, ..., то значение log2 5,53 лежит .между 2 и 3; следовательно, в жачестве аппроксимирующей должна быть выбрана функция Коэффициенты полинома в знаменателе максимально плоской (баттервортовской) функции вида S + fllS -+fl2S-2+ ... +fl2S2 + fliS + l с полосой пропускания О... 1 рад/с цепи третьего порядка. В соответствии с табл. 2.1-3, ее можно записать в виде yV(s) = W/(s3 + 2s2 + 2s+I). (18) Заметим, что W(j2) =0,124, а обратная ей величина равна 8,06, что больше 5,623, как и требуется в неравенстве (16). Пример 2.1-3. Максимально плоская характеристика, у которой е¥=1. В этом примере определения функции цепи с максимально плоской АЧХ, удовлетворяющей техническому заданию, предположим, что требуемое затухание 20- - 6 -. * . - г.. а,в'.. 0,2.. ава- - (7,06-- IW-,7 IBB-.7 вВ-.т IB-.г 60-.7 so-.- 20-.Г I -- 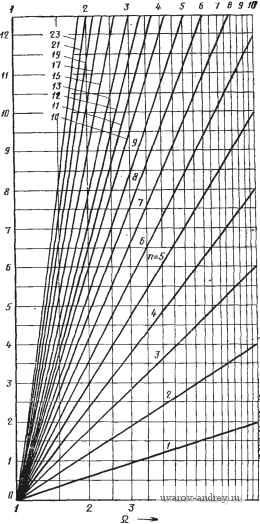 5 6 1 в 9 т Рис. 2.1-4. HoMorfdiMMa для определения порядка максимально плоской фуня- ции на границе п-олосы прапускания (со=1 рад/с; составляет 0,5 дБ, а затухание на частоте со=2 рад/с должно -быть не менее 18 дБ. Первое из этих условий можно использовать для определения величины ев (12). Заметим, что 20Ig[7V(j 0)\I\.N{] 1) ] =0,5, следовательно, ]N{] 0)\I\NQ 1) j = = (1-1-Е^)*/=1,0593. В результате получаем, что е^=0,Ш,2. Чтобы получить затухание точно 18 дБ на частоте <о=2 рад/с, мы должны иметь 201g[W(iO)/W(j2)] = 18, откуда находим lAf(j 0) /iV(j 2) =.7,943. Таким образом, необходимо удовлетворить следующему соотношению: \N{1 0)1/ yV(] 2) I == (1 + 0,122-22 )>/2 > 7,943. (19) Решая это уравнение относительно п, найдем, что оно соответствует log2 22,56, значение которого лежит между 4 я 5, т. е. окоячательяо получаем, что функция цепи должна быть пятого торядка. Используя (12), можно .в итоге найти для этой функц.ии .полином в знаменателе. Вычисления, проведенные в двух предыдущих примерах, можно упростить, используя номограммы, отображающие зависимость требуемого порядка фильтра от затухания Лпп на границе полосы пропускания (нормированной к значению 1 рад/с) и от ослабления А Q. на некоторой (нормированной) частоте Q. Такая номограмма приведена на рис. 2.1 -4*. Как ею пользоваться, показано на рис. 2.1 - 5. Через точки 1 и 2, указанные на рис. 2.1-5 и соответствующие определенным значениям Лпп и Aq на левых шкалах рис. 2.1-4, проводится прямая линия. Ее пересечение с ординатой графика справа (см. рис. 2.1-4) определяет точку 3 на рис. 2.1-5. Из этой точки проводится горизонтальная линия до пересечения с вертикалью, восстановленной в точке 4, соответствующей заданной частоте Q. Результирующая точка пересечения 5 позволяет установить порядок фильтра. Если эта точка лежит между двумя прямыми, соответствующими опреде-Рис. 2.1-5. Метод .использо- ленному порядку фильтра, то следует, вания номог.ра*.мы на рис. значение порядка, соот- ветствующее верхней прямой. Эту номограмму можно непосредственно использовать для подтверждения правильности результатов, полученных в примерах 2.1-2 и 2.1-3. 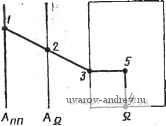 2.2. Аппроксимация амплитудно-частотной характеристики. Равноволновая характеристика В предыдущем параграфе был рассмотрен один из типов аппроксимации АЧХ, а именно: максимально плоская аппроксима- * М. Канаками. Номограммы для фильтров Баттерворта и Чебыше-1ва> [3]. Д-ip Каваками был назначен в 1973 г. президентом Токийского тех-иоло.гического института. ция. Этот частный вид аппроксимации характеризовался тем, что производные функции квадрата модуля принимались равными нулю на нулевой частоте. В результате эффект аппроксимации концентрировался на одной частоте - нулевой, а переход от полосы пропускания к полосе задерживания получился не таким резким, как это требуется в ряде применений. В этом параграфе опишем другой тип аппроксимации, для которого эффект аппроксимации распределен по всей полосе пропускания. Такую аппроксимацию называют равноволновой. Равноволновую аппроксимацию АЧХ ФНЧ можно получить, если записать функцию квадрата модуля в виде Л/(со) = Я2/[]+е2С^,И], (1) где Си (со) -полиномы порядка п. Если эти полиномы обладают свойством: OCnfo))! для Otol рад/с и СК{(а)>\ для сй>1 рад/с, то полоса пропускания будет лежать в пределах 0 рад/с и будет характеризоваться тем, что Л/(]©) тах = = Я и Л/а.а)), г„ = Я/(1+Е2)1/2. Таким образом, значение е будет определять пределы изменения АЧХ в полосе пропускания. Например, для е= 1 минимальное значение АЧХ будет на 3,01 дБ ниже, чем максимальное. Другие пары значений -е и изменения в децибелах - приведены в табл. 2.1 - 1. Полоса задерживания определяется для сй>1. В этой полосе I Л/ ) i <Я/ (Ц- Е^) /2. Полиномы Си (со), обладающие свойствами, определенными выше, называются полиномами Чебышева} Они записываются следующим образом: Ci (©) = ©; И = 20)2-1; (2) Сз{©)=4©3 Зо); {©) = 2 © С„ И-С„ , {©), где последнее выражение справедливо для всех п>\. Полиномы Чебышева можно записать также и на основе тригонометрических и гиперболических функций: С„ (©) = cos (п arc cos ©), О < ©< 1; (За) C (©) = ch(nArchcu), (36) Вшервые эти полиномы были июпользова.ны П. Л. Чебышевым в работе [4], посвященной изучению конструкции паровых машин (1899 г.). В ино-страиной литературе в связи с необходимостью передачи звуков русского языка латинскими буквами используются многочисленные варианты написания фамилии Чебышев (в разных странах по-разному), в частности, Chebyshev, icliebysheff (англ.), Tschebyscheff (нем.), Czebyszew (польск.) и др. В соответствии с этими вариантами, и чаще всего, полиномы Чебышева Обозначаются заглавной буквой Т, а не С, в том числе и в отетествен-ной ли-ературе (для полиномов Чебышева первого рода, о которых зд-есь идет речь). - яриж. ред. Графики С2 (©) некоторых из этих полиномов показаны яа рис. 2.2- 1. Равноволновые АЧХ для я=2; 5 и 10 (е = 1) показаны на рис. 2.2 - 2. Их сравнение с соответствующими графиками максимально плоских АЧХ (см. рис. 2.1-2) показывает, что за- 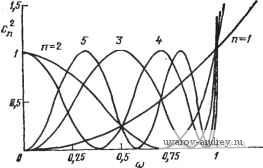 Рис. 2.2-/. Графики некоторых полиномов Чебышева С^п ( ) тухдние в окрестности частоты среза для равноволновых характеристик значительно больше при одинаковом порядке. Для достаточно высоких частот затухание составляет, конечно, величину 20я дБ на декаду по отношению к его значению на частоте 1 рад/с, как и для случая максимально плоских АЧХ. Значения модуля Л/0©) для некоторых характерных значений неравномерности АЧХ приведены в табл. 2.2-1а. Значения частот на уровне спа- Рис. 2.2-2. Амплитудно-частотные харак- - Р^ теристики равноволновых (3 дБ) функций личных значении неравно-различных порядков мерности АЧХ (амплитуды пульсаций) и различных порядков приведены в табл. 2.2-16. Эти частоты определяются из соотношения 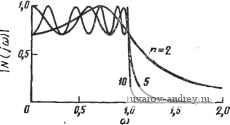 <аздБ = сЬ(-АгсЬ--у 8<1. Теперь можно использовать выражение для A(jcu) \ (1) для определения положения полюсов при равноволновой функции цепи. С учетом представления, данного для функции квадрата модуля как функции цепи, в общем случае (см. предыдущий параграф) можно записать N{s)N{-s)\N(iii;)\l,mi[\-f e C* (s/j)]. Пиль-сации ы, рад/с 5 6 7 8 9 10 5 6 7 8 9 10 -.96 -3.27 -5.61 -е.64 -12.11 .1624 -15.79 .1051 -19.57 .0677 -23.39 .8958 .8165 .6864 .5244 .3648 .2481 .8105 .6966 .5438 .3894 -1.82 -3.14 -5.29 -8.19 2635 -11.58 1732 -15.23 1123 -19.00 0723 -22.81 0465 -26.65 .8359 -1.56 .6539 -3.69 .4266 -7.40 .2465 -12.16 .1355 -17.36 .0732 -22.71 .0394 -28.10 .0211 -33.50 .0113 -38.90 .7226 .5103 .3081 -2.82 -5.84 -10.23 .1720 -15.29 .0934 -20.59 .0503 -25.96 .0270 -31.36 .0145 -36.76 .0078 -42.17 .6331 -3.97 .3031 -10.37 .1209 -18.35 .0465 -26.65 .0178 -35.00 .0068 -43.36 .0026 -51.72 .0010 -60.08 .0004 -68.44 .4896 -620 .2133 -13.42 .0833 -21.58 .0319 -29.91 .0122 -38.27 .0047 -46.63 .0018 -54.99 .0007 -63.35 .0003 -71.71 Примечание. А - амплитуда. Таблица 2.2-16 Частоты среза на уровне половинной мощности (-3 дБ) для равноволновой (чебышевской) функции цепи нижних частот с полосой пропускания О... 1 рад/с Пдтсации. .010000 .100000 .200000 .500000 1*000000 3.303615 1.в771вО 1.466904 1.291217 1.199412 1.145268 1.110609 1.067064 1.070ЭЭ1 1.943219 1.386995 1.213099 1.134716 1.092931 1.06В001 1.051927 1.040955 1.033131 1.674270 1.263455 1.156346 1.099154 1.066S17 1.050188 1.036351 1.030262 1. 24469 1.389744 1.167465 1. 93102 1.059259 1.041030 1.030090 1.02Э011 1.016167 1. 14707 1.217626 1.094668 1.053002 1.033815 1.023442 1.017205 1.013164 1.010396 1.006418 Следовательно, полюсы произведения N{s)N(-s) суть корни уравнения C\(s/i)=-или Cn(s/j) = ±]/е. Используя тригонометрическую форму для С„((о), приведенную в (3), можно запи сать С (s/j) = cos (rt arccos (s/j)) = ±j7e. (6> Значения амплитуд равноволиовой (чебышевской) функции с нормированной полосой пропускания (w=l рад/с) 1 2 3 4 5 6 ... 38 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
© 2000-2026. Поддержка сайта: +7 495 7950139 добавочный 133270.
Заимствование текстов разрешено при условии цитирования. |