пример €.6-1. Чувствительность функции цепи ЧЗОС-фильтров. В качестве примера Я'роцедуры нахождения чувствительности функдии цепи рассмотрим цепь нижиих частот третьего порядка (рис. 6.6-2,а). Применяя RLC- С7?0-(пр€образование, получим в результате структуру, показанную на рис.

Рис. 6.6-2. Схема цепи нижних частот третьего порядка в примере 6.6-I. Значения элементов даны в омах, .генри, фарадах и фарад-секундах

6.6-2,6. Сра.внивая ее с рис. 6.6-1, определяем: Zi=i?i, 2з=?з, 4=

=sCi и 25=Уб=0. Следовательно, на основе (4) N(s) можно залнсать в виде:

Л/ (S) = 1 /(I + Zi Кг + z;y, -ZY, Zi Z, Y) =

= !/[(/?! Q) + (Ri D.,) -f {Ri Q -f 3 Q) s + 1]. (5)

Исследуем теперь чувствительность этой функции к элементам ЧЗОС, т. е. рассмотрим Г как D2. Из выражения (5) находим

5Й.=5 . = 55, = 0; = 5*3=1. (6)

Используя .схему на рис. 6.1-2 при Y, = sCi2, ¥2622, Уз=5Сз2, У4=042 и y&=Go2{yi=yZi) для .реализации ЧЗОС, можно выразить Do так:

D2 = Ci2 С32 G52/G22 G42- (7)

Тогда чувствительность Ds по отношению к элементам ЧЗОС

Используя результаты, полученные в (3), находим, что чувствительность N{s) к x

U) 3 + Ь2 )/{Ь, -f 62 -f fei S -f 60), (9)

где x можно представить любой из величин С12, С32 или G52. Чувствительность к G22 или G42 есть просто взятое с обратным знаком выражение (9). Оценивая коэффициенты bi .для значспий элементов цепи, показанной на рис. 6.6-2, получаем

5 ( = (s3 + 2s2)/(s3 4- ?s2 -f 2s + 1).

Для s=jco это можно записать так:

5 (j to) (2co2 2(o4 jj6)/(i 4. (j6)j Зсо=/(1 + со ).

Следовательно (см. свойство 14, табл. 3.1-1).,

5 О ) = (2(в2-2со* -соб)/(1 -f ©б).

Вид .функции (12) показан на рис. 6.6-3, из которого следует, чтО: чувствительность Л'(]0)) к x равна или меньше 1/2 в полосе Пропускания от О

(10) (И) (12)

до 1 рад/с. Чувствительность за пределами полосы прбпускйяйя;-ШЧя она и больше, обычно играет меньшую роль. .

Многапараметрическая чувствительность (см. § 3.2) функции цепи по ог-ношётно ко всем элементам ЧЗОС-

.d\N (ja)

где Xl = Cl2, X2=G22, XsCss, XA=Gfi, Xs.= G52.

Следовательно,

d\N (j m) I 2co2- 2co -со . / d dCz

- Л~ .-с

dC2 dGb2

(13)

(14)

l+co .... V С^-г

Очевидно, соответствующий выбор допусков для отдельны.х пассивных Шъ. мантов реализации ЧЗОС; позволит минимизировать эту чувствительность..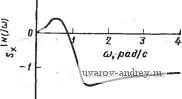

-21.

Рис. 6.6-3. Чувствительность модуля для цепи на рис. 6.6-2

г

г

Рис. 6.6-4. Схема ФВЧ третьего .порядка, рассмотренного в при:ере 6.6-2. Значения элементов даны в омах, генри, фарадах

Рассмотрим теперь метод моделирования пассивной цепи с помощью искусственной индуктивности. Чувствительность функции ц€пи для этого метода находится аналогично предыдущему.

Пример 6.6-2. Чувствительность функции цепи для реализации фильтра с искусственной индуктивностью.

Схема двусторонне нагруженного ФВЧ -Третьего порядка показана на рис. 6.6-4. Требуется найти чувствительность модуля передаточной функции по напряжению к аждому из пассивных элементов искусственной индуктивности, использованной для реализации. Цепь обобщенного иммитанса на рис. 6.1-2 можно использовать для получения искусственной индуктивности, если выбрать Zi=Ri2, Z2=l/sC22, 2з=/?з2, Zi=Ri2 и Z5=Rb2. Приравнивая элементы схемы на рис. 6.6-1 соответствующим элементам схемы на рис. 6.6,-4- И) считая, что N{s) = V2{s)/Vi(s), получаем

N(s) =

{C,L2CsRi)s ..............

~ ;С, Ц Сз R,+Ri Ci La С3) s3+(ii Cj, C3 Ri+Ц, Cj-f C L) s-f (C3.R Q s+l

(T5)

Вычисляя чунствительносгь коэффициентов к L2, находим = 1; Sl I, (Cj + Сз)/[К, Ci Сз R + (C + C3)] = 1/2; S = Г (16)

Чувствительность других коэффициентов к равна нулю. Величина Lz, полученная как результат реализации искусственной инQrlKтивнocти, определяется как

L2 = /?12 С22 Rs2 RbilRii (17)

Из (3) следует, что чувствительность передаточной функции

3 bf, + biS+ bs + bsif j

где X может быть любой из величин R12, Сц, Ri2 и Лъ2. Подставляя s= =j(o, .получаем

sn (j со) + tDi! + (в')/(1 + w ) - j (й) + (йб)/(1 + o))j. (19)

Следовательно, для x=Ri2, С22, J?32 и Яъ2 имеем

S]W (j to) I (2 4- fi>2 6)1 д, ) (20)

в то время, как для х=Мц получаем выражение (20) с отрицательным знаком. 4

Анализ чувствительности указанных выше типов можно использовать для того, чтобы предсказать влияние изменения значений элементов на характеристики фильтра. В качестве иллюстрации рассмотрим пример 6.6-2. Если конденсатор, используемый в искзсственной катушке индуктивности, майларовый с температурным коэффициентом емкости (ТКЕ), равным 600-10 /° С, то при сй=1 рад/с, Scj j) I =2. Поэтому dAf (jco) /Л/(]оз) при (а=\ рад/с равно 1200-10 /°С. Это приводит к изменениям на 1,2% величины Л/(]1), обусловленным ТКЕ С22, при изменении температуры на 10° С. Аналогичный анализ чувствительности можно провести для других пассивных элементов активных RC-подцепей, а также для других элементов фильтра.

Другим методом моделирования пассивной цепи, описанным в этой главе, был метод структурно-перекрытых реализаций. Он был использован для синтеза ФНЧ и ПФ, функции фильтрации которых не имели конечных нулей на оси j.co. Метод требовал, чтобы иммитансы лестничной цепи реализовались как передаточные функции по напряжению. Анализ чувствительности соответствует общей процедуре, описанной выше, а именно: он включает в себя нахождение S ж, где Г - пассивный элемент, а х - любой из параметров активной /?С-подцепи, которая реализует передаточную функцию по напряжению синтезируемого пассивного элемента. Для случая ФНЧ элементы общей схемы на рис. 6.3-1 описываются соотношениями

К, = (1 /Lj)/(s-f RilLi); Zj = {l/Cj)/(s + 1 /Rj Cj), (21)

где Ri может быть нулем, a Rj - бесконечностью. Заметим, что на этом рисунке обозначения Z я Y обратны тем, что даны на рис. 6.6-1. Для моделирования этих функций Z и Y используется

схема, показанная на рис. 6.6-5. Ее передаточная функция по напряжению

7ft(s) = V (s)/V.-(s) = (-l/iftCj,)/(s+l/7? Q,). (22)

Выбор необходимых элементов осуществляется с помощью табл. 6.6-1.

В структурно-перекрытой реализации последовательные или щунтирующие иммитансы могут иметь форму Ui+i Vi. Когда моделируется такой иммитанс, возможно, ,

что как Ui, так и Vi являются функциями одного и того же параметра х подцепи, с помощью которой осуществляется моделирование. В этом случае вы- fr

Рис. 6.6-5. Схема для моделирования фунгадаи (21)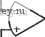

+ Vo

числение 5(>ж можно провести непосредственно, используя то, что

\ 1=0

A(s)-

\i=0

B{s) (23)

и не ища промежуточных чувствительностей S°i г и 5*1 j., как это сделано в (3).

Таблица 6.6-1

Выбор элементов для структурно-перекрытой реализации

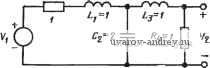Puc. 6.6-6. Схема ФНЧ третьего порядка, рассмотренного в примере 6.6-3. Значения элементов схемы даны в омах, генри, ф|араиах

Пример 6.6-3. Чувствительность функции цепи реализации структурно-перекрытого фильтра. Требуется найти чувствительность функции цепи к Rn, R21 и Си схемы на рис. 6.6-5, есл,и используется метод структзфного перекрытия для реализации ФНЧ, схема которого показана на рис. 6.6-6. Его передаточная функция по напряжению

N (s) = V2 (s)/Fi (s) = RJ[(Z-i Сг Lg) -f {R C L3 + -i C2 Ra) +

+ (Ll + L3 -f Cs Ri) s + (i?i -f Rd] = 1 /(2s3 + 4s2 + 4s + 2). (24) Из табл. 6.6-1 находим Ri = RiilR2i и Li=RiiCi, для схемы иа рис. 6.6-5 с k=l. Следовательно,

N (S) = RiRi/HRii Сп С2 Lg) + (R C L3 + R R21 Сц C R s +

+ iRu R2i Сц + Rn L3 + 11 C2 Ri) s -f (i?ii + R21 Ri)]. (25)

Ненулевые чувствительности коэффициентов то отношению к Ru, R21 и Си в предположении, что эти элементы имеют единичные значения, равны:

Sj =S= =1; 8% =1;

= ?2ii?4/fco =1/2; = R21 Ls/bi = 1/4;

= Rii R21 Cl, Q RJbi = I/2; S?f = 1. Используя эти результаты в (23). получаем

(26)

1 l+3s + 4sg+2s

2 l+2s + 2s2 + s3 1 l+3s + 4sM-s3

(27a) (276) (27b)

2 l+2s-f2s24-s3

Подставляя s=i<B решая полученные уравнения для вещественных ча-£тец, находим

с|л;Осо) 1 1+со + 2соу

R. - - 2 l+co

2 l + co

<> 2 I + со *

(28а) (286) (28в)

Анализ чувствительности, необходимый в случае применения метода структурных реализаций к полосовым функциям, аналогичен описанному выше. В таком случае иммитансы будут иметь вид, показанный на рис. 6.3-И. Если порядок полосовой реализации равен четырем или выше, вычисления- становятся значительно длиннее. В этом случае разработчику будет полезна информация о чувствительности, полученная экспериментально или путем машинного расчета.

Другой метод реализации, представленный в этой главе, - это метод ОРБ. Анализ чувствительности такой реализации легко осуществить путем определения Sxn и 53,: каждого из блоков второго порядка и сопоставления их с общей функцией цепи. Из (1), § 6.4, следует, что если все блоки второго порядка имеют идектичные передаточные функции Ti{s), то общая функция цепи

N{s) = Vis)fVy is):A(s)/Bis)

Используя табл. 3.1-1, можно записать

xxx TAs)

lYajTsV 1.(29) 1=1

Sr%,S/\ (30)

Sj%-n; Sf%(j]jajTi(s)Al( l + j]ajTi(sy]. (31)

. Следовательно, (30) примет вид

+ in-j)ajTiis)

= S[/W(s)]. (32)

=1

Чувствительноть модуля Л^(]Сй) к x равна Sr =Re[Sr M(j )J.

(33)

..Учитывая, что Sj и /И(jco) -величины комплексные, можно Переписать (33) в виде

5lA/(j4o)i e[Sli>]Re[M{i(o)] - ]m[Sli]lm[M{}(o)]. (34)

;i. Полагая, что а>п и Qp - функции х, получаем

cr,(ja) <jr.(Jco) cl/Qp , cr,-(jffi) с.ш„

где

7, (s) = [Яо (co /Qp) s]/[s + M) s + co2]. .: После ряда алгебраических преобразований найдем

(35) (36)

(37) (38)

biQpiaJa-a/a). (39)

Так как Re[5/*]=Sl* T0 из приведенных выше равенств подучим

biQp

(©/© + © /©),

где

bj Qp

1-f b-

:; .. Rel5;.-< ].=-i-5y*

Аналогично можно показать, что

Im = = arg [Т, (j co)]Sf 1.-< > =

= arg [Ti (j CO)] {Srlf < >J Slp + s:t.-i > 55?

Оценка S и SJ . дает

,aig[r.(juj]

1/Q.

arg [Г, (jco)] (1+fc)

.2ч

(40>

(41)

(42)

arg[r(jCO)] Qp(C0/C0n + C0n/€u)

(l+fc?)arg[rajco)l Подставляя (42) и (43) в (41), получаем

(44)

Желаемое выражение получается путем подстановки (40) и (44) в (34):

Smm I = (Re [М (j CD)] + Im [М (j со)]} bi

\e[M(jco)]+

Im [M (jco)]

(45)

Хотя оценка (45) в общем виде сложна, можно показать, что 5ж з' > имеет кратные нули чувствительности в полосе пропускания; это приводит к тому, что характеристики чувствительности ОРБ-фильтров близки к характеристикам структурно-перекрестных (фильтров и других реализаций, для которых используются методы моделирования пассивных цепей.

П|рИ1мер 6.6-4. Чувствительность функции цепи реализаций ОРБ-фильтров. Требуется найти функцию M{s), определенную в (32) для ПФ второго порядка с максимально плоской АЧХ, добротностью Q=5/ l/2 и средней частотой 1 рад/с. У передаточной функции нижних частот fco=.l и bi=y~2. Коэффициент усиления реализации Яо=1/2, и блоки второго порядка имеют добротность Qp = 10 и > = 1. Следуя процедуре, изложенной в § 6.4, находим ао=1, ai = 0 и 02=1/2. Полученная в результате ОРБ-структура будет иметь только одну петлю обратной связи, как показано на рис. 6.6-7. Оценка M{s) дает

M{s)=-

2 + aTi{s)

2 (s2+s/10+ 1)2

(46)

I + £i Ti (s) + 2 Ti (s)2 (s2 + s/10 -f 1)2 + (s/10)2

Следует .заметить, что M(s) имеет нули в точках, соответствующих полюсам Ti{s). Так как полоса пропускания всего фильтра располагается на участке оси jco вбливя нулей на плоскости комплексной частоты, чувст-ввтельяость в полосе пропускания будет минимизираватвся. В действительности положение несколько усложняется из-за наличия членов bi. ф

-о

Рис. 6.6-7. ОРБ фильтра для примера 6.6-4. Сопротивления даны в омах

Последний метод синтеза, представленный в этой главе,- параллельно-каскадный. В этом методе процедура синтеза непосредственно основана на использовании коэффициентов N{s). Следовательно, анализ чувствительности достаточно прост. В форму.пе (16) элементы цепи выражены через коэффициенты. Выражая коэффициенты через элементы цепи, получаем

2fe-1 = ; bi-i Cgi + Сц.

Следовательно,

(47)

i ь„,-

(48)

Эти чувствительности коэффициентов можно подставить в выражение

2 S/asO A(s)~ 2 SibiS4B{s), (49)

чтобы найти чувствительность N{s) к любому параметру цепи х.

Так как каждый коэффициент функции цепи, реализуемой параллельно-каскадным методом, зависит только от одного или двух пассивных элементов, чувствительность этой реализации не так хороша, как чувствительность, полученная предыдущим методом, рассмотренным в этом параграфе. Однако одно из преимуществ параллельно-каскадного метода состоит в том, что активные элементы, т. е. КОИ, не оказывают никакого влияния на реализацию. Это, конечно, соответствует действительности до тех пор, пока эти элементы идеальные.

6.7, Активные элементы цепи

В этом параграфе рассмотрим, как неидеальные свойства операционных усилителей влияют на характеристики активных элементов цепи в целом (см. элементы, введенные в §§ 6.1 и 6.2). Среди них были ЦОИ, искусственные индуктивности, ЧЗОС и КОИ. Рассмотрим сначала схему ЦОИ, первоначально введенную в § 6.1. Она состоит из пяти полных проводимостеи Yi{s) и двух операционных усилителей, соединенных так, как показано на рис. 6.7-1. Схема, пригодная для расчета входной у^

полной проводимости Уех =

Рис. 6.7-1. Схема ЦОИ

=/(s)/yi(s), когда коэффициенты усиления операционных усилителей не бесконечны, приведена на рис. 6.7-2. Для нее

Лаг Лд, П + Ац П (К, -Ь П) -f Ajz (П + П) + +(К2 + Кз)(К^ + К,).

. +(2 + Уз)(К4+К5)]

удобства изъято обозначение

где для удобства изъято обозначение функциональной зависимости (s) при написании членов в правой части. Интересно отметить, что числитель и знаменатель идентичны, за исключением члена, содержащего AdiAd2- Легко видеть что при стремлении этого произведения к бесконечности Увх(8) стремится к величине, приведенной в (6), § 6.1, а именно: Fi (s) Уз(5) У5 (5)/У2 (s) У4(8). Данную схему ЦОИ можно использовать для реализации как искусственной индуктивности, так и ЧЗОС. Рассмотрим сначала искусственную индуктивность. Если выбрать Y2{s)=sC2, а другие полные проводимости Yi=Gi (i=T, 3, 4, 5), то имеем (вариант 1)

(S) = 1 /Пх (S) = (Сг GjGi GsGs)s- sL,g.

Кроме того можно было бы выбрать У4 = 5С4 и Уг = Ог (i=l, 2, 3,

5), что дает (вариант 2)

j2 W

С, Go G5

s= sL

eg-

г

Рыс. 6.7-2. Схема ЦОИ с операционны- Рис. 6.7-3. Реализация искус-ми усилителями, не имеющими беоконеч- ственной индуктивности с по-но большого коэффициента усиления мощью ЦОИ

Принимая вариант 1, получаем схему на рис 6.7-2. Полагая, что Adi(s) и Ad2{s) представлены однополюсными моделями [см. (17) приложения Б], можно переписать (1) в виде

Увх (S) = Gi [Gi Gs G5 + GBj is + Юаа) Оз (Gj + Сь) + GB (s + Юд) s G X

s GBi GBs Cs G4 + GBi (s -b co) G3 (G-bGj) -b GB X X (G4 + G5) -Ks + таг) (s + co2) (s + G3) (G4 -f G5)

X (s + соя) s Cs (G, + G5) -f (s -f coai) (s -f cDaa) (s C -f Gj) (G + G)

s Cs o4

Пренебрегая членами, которые не содержат GBi или GBz, ролучаем . .,

; - ~ t [GBs Q (G4 + G5)] + [GBj GBa GJ s [coa GBj G3 (G4 + Gb]

-K6BiGBsG3G5)

Преобразуя (5), находим / .

[Ca (G4 + G5)/Ggi G3 G,] + [(G4 + G5)/GBa G -j- cogj C X [(G4 + G5)/GBi G4] s + 1 + [шаа Оз (G4 + G,)/GB2 Gd/s

X{G + G,)/GBiGsG,)]s+ly g.

Примем s=jcu, тогда, полагая, что \C2{GA-\-Gb)lGBxGzGb\4y< и используя величину, обратную результату, получаем

Z S J * [ -}/(i(a2<s(Gi+G)/GB2C2G]+i(i>[{Gt+G)/GBiG]

- Gi Ga Оз I 1 + j со [(G4 + Сб)/СВа G, +co<,i С^ (G4+G5)/GBj G3 Сб] /

, :(7)

j . Чтобы проанализировать это выражение, определим функцию (со) с помощью соотношения

Re [Z О со)]

где Z(j-o)) - входное полное сопротивление неидеальеой искусственной индуктивности, моделированной как последовательное соединение сопротивлений и идеальной индуктивности. Фаза

arg[Z(jco)] = arctgiIgMJ. (9)

RetZQcD)]

Если Q велико, то Im[Z(jcD)] >Rel[Z(jco)], так что арктанген-сную функцию в (9) можно упростить. В результате имеем

arg[Z(jco)] :; jt/2-Re[Z(jco)/Im[Z(jco)]. (10)

Используя (8), получаем .

arg[Z(icD)] ;jt/2-l/Q(co). (11)

Решая полученное выражение относительно Q(cu) и применяя результат к случаю искусственной индуктивности путем использования (7) для определения a;rg[Z(Jcu)], находим

g4 + g5 , OarCAGi + G G + G

J coasGs{Gi + G)

GB2 g5 GBi Gs GB, G4 J co GBa G4

(12)

где Q(icu)>l. Это выражение можно переписать:

(ю)л;--

.G)(-~--)+io+л.±sJ±±

t-r BJQg GBGJ ЛхСзС, co ЛаСаС^