полностью идентичными и указанные схемы будут иметь те же характеристики.

Для получения практически таких же результатов можно использовать более простую реализацию, чем на рис. 6.3-2. Чтобы показать это, запишем (2) в виде

Vn = {Vi-y,)Yi, -V2 = (yn-Vts)i-Z,); (За), (36)

-Vis=i-V, + V,)Y3, V,-=i-Vis + Vi,)i-Z,); (Зв), (Зг>

Vib=C/,-V,)Y (Зд)

Структурная схема цепи, реализующей эти уравнения, показана на рис. 6.3-3. Заметим, что при этом не требуются инверторы с единичным усилением. Следовательно, реализация цепи упрощается. Перед переменными V2, Угз и т. д. в (3) стоит знак ми-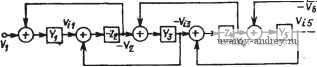

Рис. 6.3-3. Упрощенная структурная схема для моделирования цепи на

рис. 6.3-I

нус. Это значит, что передаточные функции от переменной Vi к этим переменным будут фактически инвертирующими, а не не-инвертирующими. Кроме того, все передаточные функции по напряжению, обозначенные Zi, будут теперь инвертирующими. Это приведет к тому, что указанные инвертирующие передаточные функции окажется легче реализовать, чем неинвертирующие.

Можно сформировать другую реализацию, если выразить (2) в виде

-Vn = {Vi-Vd{-Yi); -V, = {-Vn + Vts)Z2, (4а), (46) Visi-V + Vdi-Ys); V, = iVt3~V,s)Z,; (4в), (4г> -Vt, = iV,-V,){-Y,), (4д)

Эти уравнения реализуются с помощью схемы, показанной на рис. 6.3-4. Здесь все передаточные функции по напряжению,.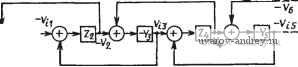

Рис. 6.3-4. Другая упрощенная структурная схема для моделирования цепи

на рис. 6.3-1

обозначенные как У являются инвертирующими. Отсюда видное, что как рис. 6.3-3, так и рис. 6.3-4 указывает на возможность осуществления структурно-перекрытой реализации.

Рассмотрим теперь применение перекрытой структуры для ре=-ализации ФНЧ, у которого все нули передачи лежат в бесконечности. В этом случае последовательные элементы Уг на рис. 6.3-1 будут нндуктивностями, а шунтирующие элементы - емкостями. Начальные и конечные элементы будут включать в себя сопротивления источника и нагрузки соответственно. Если указанная реализация возбуждается источником напряжения и имеет нечетный порядок, то конечный элемент будет таким, как показано на рис. 6.3-5,а (для п=5). Для случая возбуждения от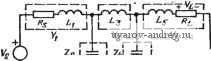

1l.s Lij

Puc. 6.3-5. Схема структуры пассивных ФНЧ: а-пятого порядка (нечетная); б-шестого порядка (четная)

источника напряжения реализации четного порядка конечный элемент будет таким, как показано на рис. 6.3-5,6 (для п=6). Другие случаи рассмотрены в задачах к главе. Для рис. 6.3-5,й передаточные функции по напряжению квадратиков (см. рис. 6.3-3) можно выразить так:

Ti (S) (S) = (1 /Li)/{s + RjLi); (s) -Z, (s) = - 1/s C,;

(5a), (56)

n (s) = n {s) = 1/s La; is) = Z, (s) = - 1/s Q; (5в), (5r)

n (s) = n (s) - = (1 /4)/(s + Rl il,). (5д)

Из этих передаточных функций по напряжению T2(s) и Ti{s) можно реализовать в виде обычных интеграторов на операционных усилителях, а Tz{s)-в виде интегратора, последовательно соединенного с инвертором, или в виде неинвертирующего интегратора, используя схему на рис. 6.3-6, для которой

VMlVi{s) = 2lsRC. (6)

T\{s) и Tb{s) могут быть реализованы демпфированным инвертирующим интегратором. Термин демпфирование отражает тот факт, что его полюсы смещены от начала координат. Реализация такого интегратора показана на рис. 6.3-7. Его передаточная функция по напряжению

Vo {s)lVi is) = (-\lRCI{s+ \IR, С). (7)

Полученная в результате структурно-перекрытая реализация схемы на рис. 6.3-5,а приведена на рис. 6.3-8,а; в ней использованы инверторы и построена она в соответствии со структурой а рис. 6.3-3. Все номиналы сопротивлений резисторов представлены через отношение к выбранному произвольно номиналу

Рис. 6.3-6. Схема неинвсртлрю-щего интегратора

Рис. 6.3-7. Схема лемп-фироваиного инвертирующего интегратора

сопротивления, которое может быть таким, чтобы удовлетворить желаемой нормировке по полному сопротивлению. Номиналы емкостей конденсаторов определены через то же R и значения соответствующих элементов на рис. 6.3-5,а.

Возможны также аналогичные рис. 6.3-5,а реализации, в которых используется структура на рис. 6.3-4. В этом случае требуются только два инвертора, т. е. на один усилитель' меньше. Реализованная схема показана на рис. 6.3-8,6. Точно так же схеме на рис. 6,3-5,6 соответствует реализация показанная па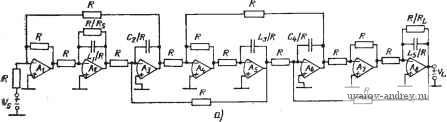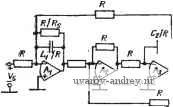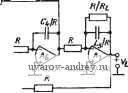

Рис. 6.3.-8. Реализации схемы на рис. 6.3-5,0, основанные на моделировании: а--схемы на рис. 6.3-3; б - схемы на рис. 6.3-4. Значения элементов схем

даны в омах и фарадах

рис. 6.3-9,G, если в качестве исходной используется структура на рис. 6.3-3, либо реализация, показанная на рис. 6.3-9,6,. если б качестве исходной используется структура на .рис. 6.3-4.. Интересно отметить, что во всех приведенных выше схемах полное сопротивление структурно-перекрытой реализации совершенно не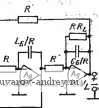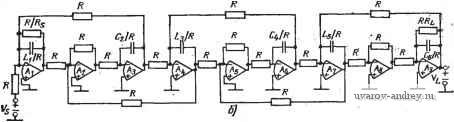

Рис. 6.3-5. Реализации схемы на ряс. 6.3-5,6, основанные на моделировании: с - схемы на рис. 6.3-3; б-схемы на рис. 6.3--4

зависит от полного сопротивления цепи-прототипа. Например, полагая, что операционные усилители идеальны, получаем, что структурно перекрытые реализации будут иметь нулевое выходное полное сопротивление и входное полное сопротивление, равное R.

На основе изложенного можно предложить следующую процедуру синтеза структурно-перекрытых фильтров.

1.. Синтезировать нормированный ФНЧ-прототип, используя приложение А.

2. Выбрать исходную структуру, взяв либо схему на рис. 6.3-> 3, либо схему на рис. 6.3-4.

3. Синтезировать внутренние элементы структурно-перекрытого фильтра, используя инвертирующие или неинвертирующие интеграторы и приняв нормированное сопротивление, равное единице.

4. Синтезировать входной и выходной элементы структурно-перекрытого фильтра, используя (7) и рис. 6.3-1.

5. Осуществить необходимое денормирование по частоте и полному сопротивлению.

Пример 6.3.-II. Структурно-перекрытый фильтр Баттерворта нижних частот третьего порядка. Требуется реализовать фильтр Баттерворта- нижних ча-

стот третьего иорядка с частотой среза 1 рад/с. Преццпалагаетсв, что ипточ иик напряжения на входе имеет внутреннее еопротивление, равное нулю.. Из приложения А получаем схему, показанную на рис. 6.3-10,с. Используя струк-турнонперекрытую схему на рис. 6.3-4 и выбирая i?=I, яолучаем схему фильтра на рис. 6.3-1 ОД Денормируя .по частоте (с .коэффициентом 1№) н по П0Л1ЮМУ сопротивлению (с коэффициентом 10*), обнаруживаем, что номиналы сопротивлений всех резисторов становятся равными 10 кОм, а номиналы емкостей .всех конденсаторов умножаются на величину 10~.

1,та 0,500

/,333J,

i В}

Рис. 6.3-10. Схема структурно-.перекрытого фильтра Баттерворта, реал!130В.чи-яого в примере 6.3-1. Значения элементов схем даны в омах, генри, фарадах

Метод структурного перекрытия, описанный выше для ФНЧ, применим также и к ПФ с нулями в начале координат и бесконечности. В этом случае ФНЧ-ПФ-преобразование применяется к каждому элементу ФНЧ-прототипа. Общий вид полученных в результате последовательных и шунтирующих ветвей показан на рис. 6.3-\\,а и б соответственно. Обычно сопротивление Ri на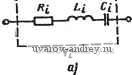

Рис. 6.3-11. Последовательные и параллельные ветви полосовой цепи

рис. 6.3-11,G равно нулю, а R, на рис. 6.3-П,б равно бесконечности. Полная проводимость двухполюсника на рис. 6.3-

Yi is) = (1/L,) sl\s + {RilLi)s-ir IJLi Q]- (8)

Полное сопротивление двухполюсника на рис. 6.3-11,6

Zj(s) = (l/Cj) s/[s + {\/Rj Cj) s+l/LjCj]. (9)

Очевидно, в случае ПФ требуемая передаточная функция по напряжению является передаточной функцией ПФ второго порядка. Следовательно, интеграторы ФНЧ-реализацйи будут^ замещаться любой схемой ПФ второго порядка, рассмотренной в нредыдущих главах. Из этого следует, что метод структурного

перекрытия дает еще одну методику получения реализаций высокого порядка на основе звеньев второго порядка. Полученные на практике реализации имеют прекрасные характеристики. Существует ряд требований, которые необходимо наложить на используемые при этом реализации ПФ второго порядка. Во-первых, реализация должна иметь возможность выполнять как инвертирующие, так и неинвертирующие операции, не требуя подключения дополнительных инверторов. Во-вторых, когда Ri = 0 или Rj=oo, добротность реализации второго порядка должна становиться бесконечно большой. Третье требование состоит в том, что реализация должна иметь возможность суммирования двух или более сигналов. Чтобы удовлетворить этому последнему требованию, следует использовать, как более предпочтительные, реализацию типа резонатора с одной петлей обратной связи и бесконечно большим коэффициентом усиления или модифицированную схему, основанную на методе. переменных состояния. Схема с бесконечно большим коэффициентом усиления потребует инвертора, тогда как резонаторная и основанная на методе переменных состояния схемы могут реализовать как инвертирующие, так и нешшертирующие полосовые передаточные функции. Чтобы получить очень высокие значения добротности с помощью реализаций с бесконечно большим коэффициентом усиления, следует применить как положительную, так и отрицательную обратные связи [65]. Если должен использоваться резонатор, то применяется схема, показанная на рис. 6.3-12, которая обеспечивает возможность суммирования. Соответствующая передаточная функция определяется выражением

/ s/RiC, yVn + V ), (10)

V s2 -f s ?i Ci -f- 1 /?a Ci Ca

Из выражений (10) и (8), a также (10) и (9) получаем соотношения, представленные в табл. 6.3-1. Эти соотношения необходимы для использования резонаторной схемы на рис. 6.3- 12 при реализации структурно-перекрытого фильтра.

Пример 6.3-2. Полосовой структурно-перекрытый фильтр Баттерворта шестого порядка. Требуется использовать метод структурного перекрытия для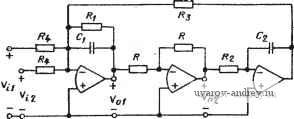

Рис.. 6.3-12. Модификация резонаторного фильтра для использования в полосовых структурно-перекрытых реализациях фильтров. Заметим: Уо1 - инвер-i тирующий, Уса-неинвертирующий выход

, V--- . Таблица

Расчетные соотношения для замены схем на рис. 6.3-11 резонатором на рис. 6.312

* JRj=i?3=JR и c,=C2=c, причем либо r, либо с выбирают произвольно.

синтеза шестиполюсного полосового фильтра Баттерворта со средней частотой 1 кГц и шириной полосы, равной октаве. Чтобы иметь устойчивый первый каскад, выберем двусторонне нагруженную структуру из приложения А с R=l. Соответствующий ФНЧ-прогогип показан на рис. 6.3-13,с.

Из § 2.4 находим, что ширина полосы, равная октаве, для средней ча.-сготы 1 рад/с составляет IfYz рад/с. Применяя преобразование ФНЧ-прототипа в ПФ-прототип с шириной полосы 2, получаем схему на рис. 6.3-13,6.

2=t: /?>-/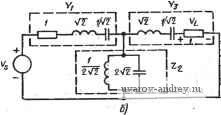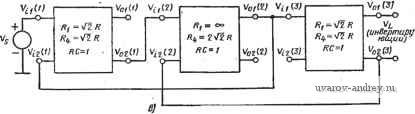

(неинввр' тирующий/

Все указанные на схеме напряжения измерены относительно земли

Рис. 6.3-13. Полосовой структурно-перекрытый фильтр шестого порядка, реализованный в примере.6.3-2. Значения элементОВ даны в генри, фарадах, омах

Если используем схему на рис. 6.3-12 для реализации лередаточных функций блоков на рис. 6.3-13,6, то сложность цепи лри выборе схемы на рнс. 6.3-3 или рис. 6.3-4 1будет практически од-инаиовой. Выбирая схему на рис. 6.3-3, получаем реализацию, показанную на рис. 6.3-13,е. Каждый из указанных на ней блоков соответствует схеме рис. 6.3-112. Если выбрать С рав-нЫМ 1 Ф, то 7?=1 Ом. Денормирование ло частоте осуществляется делением яомииалов .всех емкостей на 2л-10 Сопротивления можно выбирать произвольно н так, чтобы обеспечить приемлемые номиналы как сопротивлений, так и емкостей. Например, денормирование полного сопротивления с коэффициентом 10* дает R=\0 кОм и С=0,159 мкФ. Сопротивления Ri и R каждого блока можно вычислить, используя соотношения, приведенные на рис. 6.3-13,е.

Метод структурного перекрытия, вероятно, один из самых лучших методов реализации ПФ, так как он позволяет использовать полосовые звенья второго порядка, реализации которых рассматриваются в гл. 6, и обеспечить чувствительность реализаций, близкую к той, что дают пассивные цепи. На практике в некоторых случаях отдельные блоки второго порядка можно перестроить на несколько процентов без заметных изменений общей АЧХ. Метод структурного перекрытия также используется для реализации функций цепи с нулями на оси jco. Соответствующие подробности можно найти в литературе [66].

6.4. Основной резонаторный блок

В предыдущем параграфе было показано, как активные RC-схемы, каждая из К'Оторых реализует полосовую передаточную функцию по напряжению второго порядка, могут использоваться в качестве функциональных блоков в структурно-перекрытой реализации для получения ПФ высокого порядка. В этом параграфе рассмотрим еще один аналогичный метод, названный методом использования основного резисторного блока (метод ОРБ) [67-69]. В нем также используются в качестве функциональных блоков для построения ПФ высокого порядка полосовые реализации второго порядка. Однако этот метод имеет некоторое преимущество перед методом структурно-перекрытых реализаций, состоящее в том, что он не требует бесконечно большой добротности реализаций второго порядка. С другой стороны, как недостаток метода, можно отметить большую сложность расчетных соотношений, чем в методе структурно-перекрытых реализаций.

Общая структурная схема ОРБ порядка 2п показана на рис. 6.4-1. Каждый из блоков Ti представляет собой схему, реализу-

1 Л л

ц

Рис. 6.4-1. Структурная схема ОРБ

ющую передаточную функцию по напряжению второго порядка и имеющую (в идеале) нулевое выходное полное сопротивление. Обратная связь выхода каждого из п блоков второго порядка, соединенных каскадно, со входом операционного усилителя обеспечивается с помощью резисторов Ri(i=l, 2, п). Полная передаточная функция ОРБ

(s) -Со Ti (s) Гг (s) ... Тп (s)

Vi (s) 1-f ai Ti (s)-f Tj, (s) П ( )+ ... + П (s) П (s)...Tn (s)

где Гг (s) - передаточные функции отдельных каскадов ПФ второго порядка, а коэффициенты

aiRf/Ri,i = 0,l,...,n. (2)

Метод ОРБ может использоваться для синтеза реализаций ПФ, аналогично тому, как это было сделано для структурно-перекрытых реализаций. В качестве отправной точки процедуры синтеза рассмотрим инвертирующую передаточную функцию нижних частот п-го порядка с нормированной шириной полосы 1 рад/с

Л^нч (s) =-п--=° (3)

bn-bn-г^-+... + biS + bo Pis)

Нормированное ФНЧ-ПФ-преобразование (9), § 2.4, можно теперь модифицировать к виду

s=-(p+l)Q/p; (4)

полосовой фильтр, полученный в результате такого преобразования переменной, имеет среднюю частоту 1 рад/с и ширину полосы 1/Q. Подставляя (4) в (3) и обозначив комплексную частотную переменную р через s, получаем

N (s)-N (o]---. (5)

Vn(s)-/VH4\Q! s j - Vi is) - Di (s)

где

Предположим теперь, что все блоки на рис. 6.4-1 идентичны, и реализуем

Т, (S) = (Яо s/Qp)/{s + s/Qp +1), i = 1,2,..., п. (7)

В этом случае (1) упрощается и принимает вид

V, (s)/Vi (S) = i-uoH-s /Qp/D2 (s), (8)

где

D.(s)-(+s+iy+v°- -+ (>+ °-. (9)

Применяя биномиальную теорему к (s), получаем

i=0 V t

n-i\

< i )

X(s2+l) -W(s/Qp)+i. (10>

Цепь обратной связи на рис. 6.4-1 получается путем приравнивания (8) и (10) к (5) и (6); в результате имеем

aoH-/Q- = Hb,/Q-; (11>

-М--А 1 n-K,ki,2..... . (12).

Один из путей решения (11) и (12) состоит в том, чтобы принять

H,= l/c,Qp = Q/c, (13)

где с - произвольная постоянная, выбираемая по возможности так, чтобы сделать а,- неотрицательными. Подставляя (13) в (11) и (12), получаем

ао==НЬ,; (14>

(15)

\k } i=i \k-tj J

где в (15) Gft явно выражено через Gi, йг, аи-и Таким образом для выбранного значения с можно получить все коэффициенты Gi, G2, -, а-п.

Можно найти из (15) решение для an, выраженное явно через с, п, k и Ьг. Как получается каждое значение аи, видно из формулы

n-i\ k-i

(16)

где принято, что 6п=1. Выражение (16) можно проверить путем прямой подстановки в (15) и осуществления необходимых преобразований.

Диапазон изменения с, для которого сохраняется неотрицательность Gft, зависит от коэффициентов bi ФНЧ-прототипа. Относительно (16) интересно отметить, что ап=Р{-с), где P(s) - полином в 31наменателе, определенный в (3). Так как P(s) является (строго) полиномом Гурвица, то все его нули расположены в левой s-полуплоскости, т. е. Р(0)>0. Поэтому, обозначая вещественные нули P{s), расположенные ближе всего к началу координат, через -о(о>0), видим, что если 0<с<о, то а„>0. Из первого уравнения в (15) ясно, что GiO, если

0<c<6 i/n. (17)

Если рассмотреть для разных случаев другие уравнения (15) и (16), то можно получить другие границы для с.