те процедуру синтеза этого фильтра, используя величины сОп, Q и Яо из выражения (1), § 4.3.

5-5 (§ 5Л). Спроектируйте ПФ с однопетлевой обратной связью на одг ном усилителе с бесконечным усилением, который удовлетворяет техническим требованиям, приведенным в примере 5.1-2. Выберите соответствующее нормирование полного сопротивления для пассивных элементов.

5-6 (§ 6.1). Дайте эскиз АЧХ фильтра, схема которого показана на рис. 3.5-6. Пометьте значения коэффициента усиления по постоянному току, частоту среза и другие характеристики этой схемы.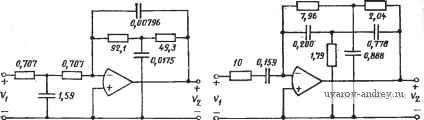

Рис. 3. 5-6. Значения элементов даны в килоомах и микрофарадах

Рис. 3. 5-7. Значения элементов даиы в килоомах и микрофарадах

5-7 (§ 5.1). Повторите задачу 5-6 для схемы на рис. 3.5-7.

5-8 (§ 5.2). Используя схему .фильтра на основе переменных стетояиня, приведенную на рис. 5.2-2, реализуйте полосовую передаточную функцию с Q=100 и резонансной частотой fn, равной 100 Гц. Примите Ci=C2=0,l мкФ и /?3=i?6=/?6=10 кОм. Найдите окончательное значение Яо из (1), § 4.3.

б) Пусть та же схема используется для .реализации передаточной функции нижних частот; каково значение Яо из выражения (1) § 4.2?

в) Пусть та же схема используется для реализации фунвдии верхних частот; каково значение Яо из выражения (16), § 4.3?

5-9 (§ 5.2). Используя резонаторную схему иа рис. 5.2-4, реализуйте полосовую передаточную функцию второго порядка с добротностью Q=IOO и резонансной частотой /п = 100 Гц, а также зиа.чением модуля Яо, равным единое [см. (1), § 4.3]. Примите Ci=C2=l,0 мкФ и Р2=Лз-

б) Повторите процедуру синтеза для передаточной функции нижних частот с теми же техническими т.ре6оеания;ми.

5-10 (§ 5.3). а) Используйте процедуру синтеза, приведенную в табл. 5.3-1, для синтеза ПФ, для которого Яо=1, fn=il000 Гц и Q=50, в случае, когда фазовый сдвиг активнсго элемента в полосе прапускания равен ±180°.

б) Повторите задачу для случая, когда фазовый сдвиг равен 0°.

5-11 (§ 5.3). а) Для фильтра, синтезированного в задаче 5--10, определите [если ам.плитуда напряжения на выходе ФВЧ равна I В (двойное пиковое значение)], чему равны амплитуды напряжений иа выходах ФНЧ и ПФ, когда частота входного воздействия равна сй=сОп/10?

б) Повторите задачу для случая, когда частота на входе (о=со .

в) .Повторите задачу для случая, когда частота на входе <в=10(Вп. 5-12 (§ 5.4). Чему равно избыточное запаздывание но фазе, вносимое

инвертирующим .интегратором, схема которого приведена иа рис. 5.4-1, с иа-

фаметрами: fHc = l кГц, fa=10 Гц и GB=1 МГц для сигналов низкого уровня на частотах f = GB/100, GB/50, GB/10 и GB/5?

I 5-13 (§ 5.4). Используя приемы, аналогичные тем, что приведены в §5.4, найдите избыточное запаздывание по фазе демпфированного интегратора, схе-ija которого дана на рис. 3.5-13. Считайте, что Ad{s) определяется (17) из приложения Б, а со изменяется в пределах Шо< <*;(B<GB.

1 5-14 (§ 5.4). Найдите положение нулей и полюсов передаточной функции по напряжению ддя интеграла на рис. 5.4-1, если Ad{s) определяется (17) из приложения Б, а Ro не равно ну-

Рис. 3.5-13 -

то. Считайте, что MRC-GB и Ша= 0. Сделайте эскиз асимптотических амплитуд-но- и фазочастотных характеристик при замкнутой петле обратной связи, если l/i?oc<4GB.

5-15 (§ 5.5). Иопользуя реализацию, основанную на переменных состояния, приведенную в табл. 5.3-1, найдите максимально возможное значение / в герцах, если Q =10, а GB=1 МГц и если разница между q я qo должна быть не более 10%.

5-16 (§ 5.5). Повторите задачу 5-15, но для резонаторного фильтра, схема которого .приведена на рис. 5.2-4.

5-17 (§ 5.5). Используйте фильтр на основе переменных состоякия, схема которого дана на рис. 5.2-5, для реализации всепропускающей цепи второго порядка, имеющей fzo=jfj>o=10 кГц и Q-p=-qz=10.

5-18 (§ 5.5). Повторите задачу 5-17, если q равна бесконечности.

5-19 (§ 5.5). Чему равны Ti и Т2 для рис. 5.5-3 (положите ЛГ=100), если со = 1000 рад/с и q=500?

5-20 (§ 5.6). а) Найдите чувствительность \SiQg\ .для реализации фильтра, основанного на методе переменных состояния, в которой q=10, f = = 10 .кГц, е=1, RelR5=0,l и R7=oo. Примите GB операционного усилителя равным 1 МГц.

б) Найдите фактическое положение полюсов этого фильтра. Каковы фактические значения Q и f ?

в) Найдите приблизительные положения полюсов, используя рис. 5.6-5, для случая, когда }п увеличивается до 60 кГц.

5-21 (§ 5.6). а) Найдите чуБ.ствительность резонаторного фильтра \SPi gb\, у которого q=10, f=10 кГц, Ji2=R3=Ri=Rs=Re==R, ci = C2=C и Ri=QR. Положите GB операционных усилителей равным 1 МГц.

б) Найдите фактическое положение полюсов для этого фильтра, используя (И). Каковы при этом фактические значения q и f ?

5-22 (§ 5.6). Найдите приблизительное положение полюсов по рис. 5.6-6 для случая, когда fp из задачи 5-21 увеличивается до 25 кГц. Каковы фактические значения Q и fn? Считайте, что (Bi=C07,/Q, (В2=Шп и Ri/Ri=Ho=l.

5-23 (§ 5.7). Резонаторная схема на ,рис. 5.7-1 имеет операционные усилители, у которых Ло=105 и GB = 10* Гц. Для схемы, реализующей функцию фильтрации с добротностью qo=10, найдите частоту, при которой она стано-

вится неустойчивой. Для процедуры синтеза примите i?2=i3=i?4=i?5=i?6=R,

6-24 (§ 5.7). При каком значении Qo фильтр, описанный в примере 5.7-1, становится неустойчивым?

5-25 (§ 5.7). Используйте схему на рис. 5.7-3 для синтеза ПФ с Qo= =5, / 0=50 Гц, Яо=1. Выберите ЛзЯъ=Яе=10 кОм и Ci=C2=3-10- Ф.

5-26 (§ 5.7). Используйте схему на рис. 6.7-5 для реализации ФНЧ, удовлетворяющего тем же техническим требованиям, что и в задаче 5-25.

5-27 (§ 5.7). Покажите, что чувствительность St модифицированного ПФ второго порядка на усилителях с бесконечным усилением, схема которого показана на рис. 3.5-27, равна нулю, если slGB:$> {s/GB)\ Оба уси лителя идентичны и имеют частотную характеристику, определяемую выраже нием Ad(s)=-GB/s. (Указание: рассмотрите сначала только пассивную цепь, обведенную пунктирными линиями, и запишите уравнения для узловых напря жений IB точке соединения двух конденсаторов Сз и инвертирующего входа А Затем используйте ограничения, свойственные усилителю, и решите уравнения относительно VVVi.)

Puc. 3.5-27

5-28 (§ 5.7). Используя приемы, рассмотренные в § 5.7, найдите добротность реализации, основанной иа методе переменных состояний (см. рис. 5.7-8,6), и покажите, что она не зависит от произведения коэффициеита усиления на ширину полосы операционного усилителя, если усилители согласованы. (Указание: в этой задаче может помочь материал, изложенный в § 5.5)

МЕТОДЫ МОДЕЛИРОВАНИЯ ПАССИВНЫХ ЦЕПЕЙ

В § 1 гл. 4 было указано, что существуют два общих метода использования активных /?С-фильтров для реализации функций цепи. Первый из них рассматривался в двух последних главах. Речь идет о каскадном методе, в рамках которого усилительные iC-фильтры использовались для реализации функций второго по-

рядка, а каскадное соединение таких реализации - для получения функций более высокого порядка. В этой главе обсудим другой общий метод использования активных /?С-фильтров для реализации функций цепи. Это так называемый прямой (непосредственный) метод, который характеризуется тем, что функции фильтрации любого порядка реализуются с помощью одной схемы.

В первом методе непосредственного синтеза схем, который будет рассмотрен вначале, процедура синтеза начинается с пассивной цепи-прототипа и затем используются активные /?С-цепи для моделирования определенных звеньев (частей) пассивной реализации. Такой метод называется методом моделирования пассивной цепи. Его преимущество заключается в низкой чувствительности, в основном соответствующей пассивной цепи-прототипу. Кроме того, так как таблицы значений номиналов элементов для реализаций пассивных цепей уже имеются, процедура синтеза смоделированных реализаций становится очень простой. Преимущества и недостатки этих методов перечислим при рассмотрении каждого отдельного типа фильтра.

6.1. Элементы активных цепей. Моделирование индуктивности

В этом параграфе начнем рассматривать некоторые типы активных элементов, используемых в методе моделирования пассивных цепей. Такие элементы лучше всего характеризуются с помощью обобщенных параметров четырехполюсника {АВСО-иат-рицы). Они определяются уравнениями вида

напряжения и токи четырехполюсника показаны на рис 6.1-1, отдельные обобщенные параметры выражаются в виде

Л(5) =

C(s) =

his)

B{s) =

Vi{s)

h(s)=0 -his)

(s)=0

- his)

V2 (s)=0

(2a) (26)

В качестве примера может служить т неиивертирующая реализация ИНУН на рис. 4.1-2,а, для которой Л (s) = + =Ri/{Ri-i-R2) и B(s) = C(s)=Z)(s)=0. v. Из (2а) и (1), § 4.1, следует, что A(s) обратна передаточной функции по напряжению данного устройства. Вход-вх ное полное сопротивление Zbx(s) четы- четырехпо-

рехполюсника, нагруженного на пол- дюсника, нагруженного полное сопротивление, как показано на ным сопротивлением

рис. 6.1-1, легко найти, если взять отношение отдельных уравнений и использовать соотношение ¥2(5)=-/2(s)iZi(s). Тогда

Iiis) C(s)VAs)-D(s)IAs) C{s)Zi(s)+D(s)

Теперь можно определить некоторые классы активных элементов цепи через ограничения на их обобщенные параметры. Существуют два общих класса активных элементов, а именно: конвертор обобщенного иммитанса (КОИ), который умножает нагрузочное полное сопротивление на величину A{s)fD(s) и инвертор обобщенного иммитанса (ИОИ), который умножает полное сопротивление нагрузки на величину C{s)/B{s) и инвертирует его. Эти два класса активных приборов и некоторые конкретные приборы в рамках приведенной классификации сведены в табл. 6.1-1. Другие подробности можно найти в литературе [56-58].

Таблица 6.1-1

Активные четырехполюсные элементы

Активные приборы*

Обобщенные параметры

Ограничения

Входное полное сопротивление

КОИ (конвертор обобщенного иммитанса)

КОИ (конвертор отрицательного иммитанса)

КПИ (конвертор положительного иммитанса)

¥=0

¥=0

А<а

или О<0

Л и £> те же

А

2вх = -гг.

ИОИ (инвертор обобщенного иммитанса)

ИОИ (инвертор отрицательного иммитанса)

ИПИ (инвертор положительного иммитанса)

Гиратор

¥=0

¥=0

В<0 или С<0

В и С

В=1/С

С Ч

Для конверторов (инверторов) обобщенного и отрицательного иммитансов сокращенные обозначения совпадают, однако ниже автор пользуется только понятиями конвертор (инвертор) обобщенного иммитанса, поэтому сокращения КОИ в ИОИ относятся только к ним. - Прим. пер.

Реализация обоих этих элементов, показанная на рис. 6.1-2, вероятно, наиболее широко используется на практике. Она была предложена в 1969 г. [59, 60] и выпускается промышленностью, как интегральная схема (ATF 431 Gyrator, Атретех Electronic Corp., Slatesville, R. I.; TCA 580 Gyrator, Signetics Corp., Sunnyvale, Calif.). Схема на рис. 6.1-2.a, в которой Zs(s) рассматри-

вается как полное сопротивление нагрузки, имеет обобщенные па раметры

Л(5)=1; B(s) = C{s) = 0; D(s) = Z,is) Z(s)/ZAs) Z,is)l/KAs).

Таким образом, этот четырехполюсник является КОИ. Величина Kc{s) называется постоянной КОИ. Так как A{s) = l, то он иногда называется токовым КОИ {КОШ)К Схема на рис. 6.1- 2,6 имеет следующие параметры (Z4 (s) - полное сопротивление нагрузки):

Л(8) = Д(5) = 0; Bis) = Z,(s); С is) = Z(s)/Zi(s) Zis). (5)

I--------------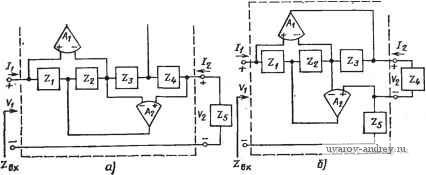

Рис. 6.1-2. Схема конвертора обобщенного иммитанса, использованная для реализации цепи обабщенного иммитанса

Таким образом, этот четырехполюсный прибор является реализацией ИОИ. Если рассматривается только входное полное сопротивление, то обе схемы на рис. 6.1-2 - идентичны. Входное полное сопротивление при этом имеет вид

вх (S) = Zi (S) Z3 is) Z, {s)/Z (s) Z, (s). (6)

В этом случае прибор называется ЦОИ (цепь обобщенного иммитанса) -двухполюсный прибор, один из зажимов которого заземлен. Этот прибор является исходным в технике моделирования пассивных цепей и используется здесь и в следующем параграфе.

Один из простейших подходов к моделированию пассивных цепей состоит в выборе RLC-Jxenu, удовлетворяющей определенным требованиям, налагаемым на фильтр, и замене катушки индуктивности активным /?С-эквивалентом. Полученный в результате элемент называется искусственной индуктивностью. Для

Для такого четырехполюсника часто используют сокращенное обозначение КОСТ. -Ярилг. пер.

Здесь и ниже автор не использует понятие гиратор , а пользуется п©-нятием искусственная индуктивность . Термин гиратор фигурирует лишь в табл. 6.1-1. - Прим. пер.

этой цели идеально подходит ЦОИ на рис. 6.1-2. Если Zzis) - конденсатор, а остальные полные сопротивления - резисторы, то входное полное сопротивление ЦОИ и эквивалентное значение ин-. дуктивности равны

2Bx(s) = si?iC,i?3W4; L . = R,C2RsRjRi- (7) Кроме того, если Z4(s) -конденсатор, то получаем

Zis) = sRiR,C,Rs/R2, L,. = RiR3CiRb/R2- (8)

Искусственная индуктивность, реализованная с помощью ЦОИ, оказывается, имеет прекрасные характеристики. Если усилители Ai и Л2 на рис. 6.1-2 согласованы, то влияние неидеальных параметров усилителей на искусственную индуктивность минимально. Кроме того, так как Zi (s) - всегда сопротивление, то задать нужные токи для обеспечения смещения по постоянному току на входах усилителей не представляет большого труда (эта проблема обсуждается более подробно в следующем параграфе). Единственным недостатком указанного подхода к синтезу цепей на основе искусственной индуктивности является то, что она, будучи активным прибором, должна иметь один заземленный зажим, т. е. J?LC-nenb должна быть такого типа, где все катушки индуктивности заземлены. Это ограничивает возможности подхода, основанного на использовании искусственной индуктивности, применении его, главным образом, в ВЧ реализациях, тогда как метод, основанный на использовании ЧЗОС, который будет рассмотрен ниже, в § 6.2, может быть применен к НЧ и П реализациям. Можно, конечно, реализовать незаземленные искусственные катушки индуктивности [61, 62], но их характеристики и простота реализации оставляют желать лучшего по сравнению с заземленными катушками индуктивности.

Представляет интерес рассмотреть уровни сигналов на выходе усилителей в искусственных катушках индуктивности. Рассмотрим для этой цели рис. 6.1-3, в котором ЦОИ возбуждается источником напряжения с последовательно включенным резистором. Для Z2{s) = l/sC2 и Zi(s)=Ri(i2) получим

Voiis)/Vi(s)=l+RjR,; (9а)

Vo2(s)/Vi{s}l-RjsRsR,C2{s~RjRsR,C2)/s. (96)

Для другого случая искусственной катушки индуктивности, где Ziis) = \/sC4, имеем

1 (s)/Fi is) = l + l/sR,C, = is+l /R, Q/s; (1 Оа)

(syv, is) = 1 -Rjs Rs Rb Ci = (s-RjRs Rb Ci)/s. (106)

Из выражений для этих передаточных функций видно, что при постоянной амплитуде синусоидального возбуждающего сигнала, приложенного на зажимах Vi{s), выходные напряжения усилителей не возрастают в зависимости от частоты и, следовательно, насыщение не происходит. Однако, так как искусственная индуктивность обычно воспроизводится на зажимах Fs(s), а не на за-

ясимах Vi{s), то практически может оказаться, что более целесообразно исследовать Voi{s)JVs{s) или F02(s)/Fs(s) для случая, когда Rs - комплексное полное сопротивление. Пример такой ситуации приведен в задачах.

Этапы применения для синтеза искусственной индуктивности следующие: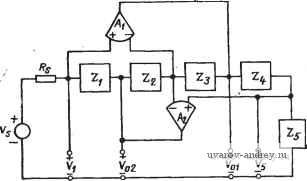

Рис. 6.1-3. Цепь обобщенного иммитанса, возбуждаемая неидеальным источником напряжения

1. Синтезировать нормированную iLC-цепь-прототип верхних частот, используя таблицы приложения А и метод, изложенный в § 2.4.

2. Синтезировать искусственные индуктивности, которые предназначены для замены индуктивностей прототипа. Использовать нормированные сопротивления и емкости.

3. Провести денормирование всех сопротивлений и емкостей. При проектировании реализации желательно провести контроль искусственных индуктивностей перед их включением в цепь. Так как указанные приборы моделируют пассивные элементы, то такой контроль легко осуществить. Например, для измерения значения индуктивности можно использовать явление резонанса искусственной индуктивности с известной емкостью. Другой путь состоит в возбуждении индуктивности с помощью источника напряжения с известным сопротивлением R и исследовании АЧХ, точка излома которой соответствует отношению L/R.

Пример 6.1-1. Фильтр Баттерворта верхних частот пятого порядка с искусственной индуктивностью. Требуется реализовать ФВЧ, используя искусственную индуктивность для моделирования пассивной цепи. Частота среза должна быть равна 10* рад/с, а сопротивления источника и нагрузки - 1000 Ом. Используя приложение А и применяя ФНЧ-ФВЧ-преобразование (см. § 2.4), получаем ВЧ цепь-прототип (рис. 6.1-4,а). Искусственные индук-тьвности легко синтезировать на основе (7), если принять \Ri=\Rs=Rt=\fi0.u, 2= 1 ф и /?5=0,618 Ом. Полученная в результате реализация показана на рис. 6.1-4,6. Чтобы получить денормированную реализацию, нужно умножить

все емкости на 10-, а все сопротивления на 10. Искусственные индуктивности должны быть настроены, как было описано выше.

Метод искусственной индуктивности, описанный выше, можно также применить и к ВЧ реализациям, имеющим конечные нули на оси J.W. Такие нули создаются при последовательном соединении емкости и индуктивности. Подсоединение одного из выводов катушки индуктивности к земле, позволит использовать метод искусственной индуктивности.

/?я=/ 1,618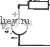

\а,Б18 \0,БЮ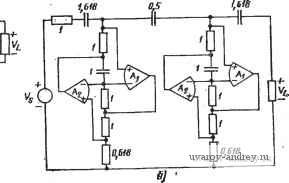

Рис. 6.1-4. Фильтр верхних частот пятого порядка, реализованный в примере 6.1-1. Значения элем.ентов даны в омах, генри, фарадах

6.2. Частотно-зависимые отрицательные сопротивления

Одним из наиболее полезных приборов для замещения пассивных цепей при использовании методов моделирования является ЧЗОС (частотно-зависимое отрицательное сопротивление). Это двухполюсный активный элемент, обозначаемый так, как показано на рис. 6.2-1, имеет проводимость

Y(s)Iis)/Vis) = D, (1)

где D - положительная вещественная постоянная. Размерность D - фарад-секунды (Ф-с). Если в выражении (1) провести замену s=j,cu, то получим y(jo))=-aD, которая является отрицательной функцией, также зависимой от частоты; она вещественна, т. е. физически соответствует сопротивлению. Следовательно, его характеристики могут быть, вероятно, описаны как характеристики частотно-зависимого отрицательного сопротивления, которое может быть реализовано с помощью ЦОИ, как показано на рис. 6.1-2. Для схемы общего вида входная полная проводимость

iBx (S) = Yi is) Уз is) Y, is)/Y, is) Y, (s), (2)

где Yiis) = l/Zi(s). Один из возможных способов реализации ЧЗОС -принять Yiis) = Y3is)=sC й Y2is) = Y4s)Ysis) = G. В этом случае (2) приводится к виду

Y,As) = iCVG)s = Ds (3)

Это и есть входная полная проводимость ЧЗОС, для которого Р^СУС. Соответствующая схема показана на рис. 6.2-2*.

Определим теперь некоторые свойства ЧЗОС. Так как его значение при 8=}(й - отрицательное вещественное, то оно является потенциально неустойчивым двухполюсником. Чтобы убедиться-в этом, рассмотрим схему на рис. 6.1-3, в которой ЦОИ везбуж-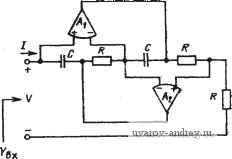

Рис. 6.2-1. Частотно-зависимое от-рицател,ииое сппротивлеине

Рис. 6.2-2. Иоиользавание ЦОИ для реализации ЧЗОС

дается от источника напряжения Vs{s), имеющего внутреннее сопротивление Rs. Так как входные напряжения, приложенные непосредственно ко входам операционных усилителей, равны нулю, то Fi(s) = F5(s). Тогда передаточная функция по напряжению от у., к Vi или Уб

Vi (s)/Vs(s) = V, (s) = 1 /11 + Rs Z, is) Z, is)/Z, (s) Z, (s) Z, (s)]. (4)

Существуют две широко используемых реализации ЧЗОС. Если Z,(s)=l/sC Z2(s)=i?2, Z3{s) = l/sC3, Z4(s)=/?4 и Zs(s)=i?s, то (4) принимает вид реализации (1)

Уг (s)/Vs (S) = (R-JR, R., R, Ci СМ + RJRs R2 Ri Ci С,) = + o)), (5)

где aoVRJRsRRiCiCs. (6)

Частота coo является такой частотой (в радианах), при которой наблюдается резонанс ЧЗОС с внутренним сопротивлением источника Rs. т. е. частотой потенциальной неустойчивости. На практике предсказанная неустойчивость может и не возникать, так как коэффициенты усиления Ai и А2 - конечны, а это приводит к тому, что полюсы сдвинуты немного влево от оси jloj. Однако передаточная функция по напряжению (4) будет и в этом случае иметь высокую добротность, следовательно, измерить ее будет физически трудно. В качестве альтернативного решения, дающего более удобные для интерпретации результаты, рассмотрим

* Хотя возможиы и другие виды ЧЗОС, приведенная здесь схема имеет определенные преимущества, обеспечивая хорошие характеристики. Она выпускается фирмой Амперекс Электроник корп. (Слейтсвидл, шт. Род-Айленд) как .микросхема гиратора ATF-431.