тика фильтра зависит не только от произведения GB, но и от мно- I гих других параметров операционного усилителя, таких как входное и выходное полные сопротивления и т. д. Одной из наиболее многоплановых и полезных схем фильтров, в которой заземлено по одному входному зажиму во всех операционных усилителях, явля-, ется схема резонаторного фильтра, представленного в § 5.2. Этг схема не только полезная и гибкая при реализации функций второго порядка, но и, как это было показано, является ценньш функциональным узлом при реализации функций фильтрации бо лее высокого порядка. Поэтому имеет смысл рассмотреть ее опти мизацию.

о---2-

Рис. 5.7-1. Схема -резонаторнаго фильтра

Основная схема резонатора приведена на рис. 5.7- 1. Анализ ее можно провести путем размыкания петли обратной связи в месте, показанном на рисунке пунктирными линиями, и исследования передаточной функции разомкнутой цепи F (s)/Fx (s). Для этого

Рис. 5.72. Каскад Л] резонаторного фильтра

сначала рассмотрим схему на рис. 5.7-2. На ней представлен первый каскад (усилитель Ai) резонаторного звена при условии, что Vi{s) равно нулю. Передаточная функция 71(5) такой схемы

Г^(,)п() -o>i(Ri/Rs)GBi

s + GBiS+aiGBi + viaiKai

где (Bai и GBi - соответственно ширина полосы Юо и произведение GB усилителя Ai. Это выражение получено в предположении, что <o>coai, И в нем принято

Фазочастотную характеристику (1) можно записать в виде arg [Ti (j со)] л; я-arctg [со GBJ{ai GB + cu i Кщ-а>)]. (3)

(Сравнивая передаточную функцию резонатора по напряжению \(20), § 5.2, со знаменателем стандартной передаточной функции Цорого порядка [см. (1), § 4.2], получаем

tOi = (Ono/Qo.

де (дпо и Qo - расчетные значения и Q. Тогда (3) можно за-шсать в виде

argfTJj©)] ;n-arctg[a)GBi/KoGBi/Qo + a)ai )no/Qo- )]- (5)

Если Q>1, то аргумент арктангенса становится большим и 5) упрощается:

argiriOo))] n/2-fcu o/Qo ) + )no/QoAi - )/G5i. (6)

1де Aoi - коэффициент усиления Ао усилителя Ai при разомкнули петле обратной связи.

Рассмотрим теперь каскад на операционном усилителе Лг (см. рис. 5.7-1). Если определить передаточную функцию У nniWnis), как Ti, то из (7), § 5.4, следует

argfTa (j )] /2 + а/со Лоа-to/GBa, (7)

гке a)2=l/i?aC2. (8)

Наконец, для инвертора Лз, который является третьим усили-тЬлем на рис. 5.7-1, определяя 7з(5) = Vx(s)/Vh4(s) из (96), §4.6, получаем (полагая RsRe)

arg[Tsii(i>)]n~2(o/GBs. (9)

Определим теперь общую передаточную функцию схемы при разомкнутой петле обратной связи как 7(s) =7] (s)72(s)73(s). Тогда общий фазовый сдвиг

arg [Т (1 со)] = arg [Т, (j со)] + arg [Т^ (] со)] +

+ arg [Ts (j со)] л^(1 /Qo + K/Qo + co/coo Л2) ( no/ ) -

- {a/GBi + a/GB + 2(ii/GBs). (10)

Из результатов, изложенных выше, следует, что инвертирующий каскад резонатора Лз имеет вдвое больший фазовый сдвиг чем каскад инвертора-интегратора. В этом состоит один из недостатков использования инвертора для получения неинвертирующего интегратора. Рассмотрим теперь, что произойдет, если величины Лог и GBi(t=l, 2, 3) стремятся к бесконечности. В этом случае (10) приводится к виду

arg [Г (j со)] (11)

Следовательно, в э^ом случае Q и Qo те же самые. Поэтому / фактическое Q можно выразить через Qo; тогда желаемое значение Q можно записать [объединяя (10) и (И)] в виде

Если воспользоваться процедурой проектирования (см. § 5.2) в которой Я2=Яз=Я4=Я&=Яб=Л {Ho=Qo для полосовой реал зации), Ci = C2=C и Ri - QoR и положить, что а)=сй о и что BCd усилители согласованы, то (12) можно упростить:

Q l/( 1/Qo + 1/Qo Ао + З/Ло-4 Wno/GB). (13

Следовательно, фактически полученная добротность выше, чей расчетная. Этот эффект увеличения добротности вызван запаздыванием по фазе в петле обратной связи, что может привести к неустойчивости цепи, если отношение оУпо/ОВ становится доста точно большим.

Пример 5.7-1. Эффект увеличения добротности резонаторного фильтре. Пусть требуется использовать резонаторную схему на рис. 5.7-1 для реал1-зации ПФ второго порядка с Q=4 и f o=38,185 Гц. .Принимаем iR2=\R3=Rt =J?5=J?6=J?, Ci=C2=C и Ri=RQo- Операционные усилители согласованы имеют следующие характеристики: Ло=10 и GB=l МГц. Фактическое значение добротности для этого фильтра при условии f-fno, можно найти из (13), откуда следует, что оно равно 10,28. Эффект увеличения добротности налицо, ф \

Выражение (13) можно также использовать для оценки значения частоты, при которой фильтр становится неустойчивым. С этой целью аппроксимируем указанное выражение, представив его в виде

Q l/(l/Qo-4 ) o/GB). (14)

Отсюда видно, что Q=oo, когда cu o=GB/4Qo. Этот результат справедлив, однако, только для малых изменений положения полюсов. В результате этого должно быть Q>10, чтобы можно было получить имеющий смысл результат. Например, используя данные примера 5.7-1, можно оценить максимальное значение © о, предсказанное с помощью (14), величиной 25 кГц. Фильтр, однако, устойчив и на более высоких частотах, так как Qo в этом примере слишко 1 мала, и использование выражения (14) не может быть оправдано.

Рассмотрим теперь, что произойдет, если инвертор-интегратор, представленный каскадами Лг и Лз на рис. 5.7-1, заменить на неинвертирующий интегратор, представленный на рис. 5.4- 10 (где R2 и 1 заменены на R5 и Re). В результате получаем модифицированную резонаторную схему, показанную на рис. 5.7-3. Фазовый сдвиг при замкнутой петле обратной связи мож-

[О начти, используя (27), § 5.4, и (6). В результате получаем ля (Ono<gfi2)

arg [Т (] ©)] [! /Qo+K/Qo Аог + (Wb)/Ao2]+ + [((o/GBa) (1 + RM -©/GBi-(©/GBg) (R/R (15)

где предполагается, что аргументы функции арктангенса малы.

я случая, когда R5=R6 и произведения ОБ операционных усилителей согласованы, получаем

arg [Т (j )] (1/Qo+/C/Qo Л + 1/Л) ( no/ )- (16)

Объединяя это выражение с (11), находим

Q l/(l/Qo + K/Qo Ао + 1/Ао). (17)

Этот результат показывает, что Q не зависит от GB, а, сле-доЕательно, для модифицированной резонаторной схемы эффект увеиичения добротности не наблюдается. Разница между ис-

Рис, 5.7-3. Схема модифицированного резонаторного фильтра

-IZ>

ходной и модифицированной резонаторными схемами иллюстрирует рис. 5.7-4. Графики, приведенные на этом рисунке, представляют две реализации ПФ, имеющего Qo=100. Значение / возра|стают вдоль оси абсцисс, начиная с 30 Гц. Исходная резона-торная схема становится неустойчивой уже на частоте приблизительно 2000 Гц, тогда как добротность модифицированного резо-

10W -

Т

io т то mm

Рис. 5.7-4. Сравнение характеристик нормального (/) и модифицированного (2) резона-торных фильтров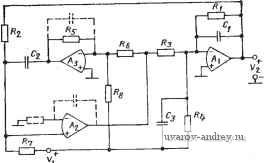

Рис. 5.7-5. Высокочастотная модификация биквадратного резонаторного фильтра

натора существенно не меняется вплоть до частоты 15 кГк. 3itf-спериментально наблюдаемые результаты находятся в хорошем согласии с (14), в соответствии с которым частота, где схема нет устойчива, составляет 2500 Гц (для GB = 1 МГц). Последнее преимущество модифицированной резонаторной схемы состоит в том, что температурные коэффициенты произведений коэффициенга усиления на ширину полосы отдельных операционных усилителей одинаковы. Таким образом, нежелательное запаздывание фазе устраняется в широком температурном диапазоне.

Общую схему ФВЧ второго порядка можно получить путчем подстановки в биквадратную резонаторную реализацию, приведенную на рис. 5.2-б, вместо инвертора и инвертирующего интегратора неинвертирующего интегратора, представленного 1на рис. 5.4-10. Полученная цепь показана на рис. 5.7-5 [55]. Техника синтеза, использованная в § 5.2, и табл. 5.2-1, справедливы и для этой цепи. Это обеспечивает гибкость общей процедуры синтеза и возможность иметь хорошие частотные характеристики. Чтобы убедиться в этом, заметим, что фактическую частоту полюса сор можно выразить через желаемую частоту полюса ©ро следующим образом:

©,©po(l-f 2©VGBi-f©VGS3)-2, (18)

где предполагается, что Ri=R2=R3=R5=R6=R; iRi ч \R7 - много больше, чем Rs и Ci = C2=C. Полюсную добротность Qp аналогично можно выразить через желаемую добротность Qpo, т. е.

п £0 /jgv

ij.n ( + RblR, + RblR, RJRb i + Cs/СЛ i + QpoCp[-------j I

Так как знаки отдельных членов в множителе, заключенном в скобки в знаменателе (19), как положительны, так и отрицательны, то при использовании приемлемой процедуры синтеза можно устранить влияние добротности произведения коэффициента усиления на ширину полосы операционного усилителя. Чтобы показать это, предположим, что GBi = GB2=GBs=GB, и определим

k = ?б/б + Cs/Ci - R/Re-R,/R8- (20)

Цель, таким образом, состоит в том, чтобы сделать k равным нулю. Из табл. 5.2-1 можно видеть, что Сз = 0 и R8 = oo требуются в случаях ФНЧ и ПФ. В этой ситуации k=0, если

Rb = Re- (21)

Аналогично для того, чтобы k равнялось нулю, в случае ФВЧ и расположения нулей на оси j© требуется удовлетворить равенству

?б/5 = (С3/2С1) [ 1 ± 1/1 -f (2С,/Сз)]. (22)

Следует отметить, что использование условия (22) часто приводит к таким значениям Re и Rs, которые вызывают значитель-

jfeie изменения уровня сигнала, снятого со средней точки соеди-1фния резисторов Rs-iRe на выход усилителя Лз на рис. 5.7-5. Эта разность уровней сигналов будет усугублять эффекты, вызванные конечной скоростью нарастания сигнала и до некоторой степени сведет к нулю результаты, достигнутые благодаря внутренней компенсации величины GB. Другая процедура полного уд ления резистора Ra из схемы (т. е. принимаем, что сопротивле! ие Rs=oo) состоит в том, чтобы отсоединить его от зажима, сое гветствующего Vi, и затем заземлить. В этом случае k про-дoJжaeт определяться выражением (20), однако резистор Rs дерствует теперь в соответствии с табл. 5.2-1, как если бы он им(л бесконечно большое сопротивление. Теперь для случая ФВН и нулей на оси jco можно принять Rs я Re а по-прежнему n0JW4HTb k=0, если положить

Cs/C2 = RjRs, (23)

где Rs подключается между инвертирующим зажимом Лз и землей.

Пример 5.7-2. Биквадратный резонаторный фильтр, независимый от GB. Пусть требуется использовать схему на рис. 5.7-5 для того, чтобы реализовать функцию фильтрации, имеющую Qpo=50, /j,o=10 кГц, Qzo=°° и го=7,5кГц. Из (28) и (29), § 5.2, получаем

(ulf, = R,/RsR,R,CC,; 4o = Re/R2R3RbC2Cs; (24а), (246) Wpo/Qpo= l/Rj Cj. (24в)

Можно выбрать R3==Rs=Re=lO кОм и С1=С2=Сз=3-10- Ф. Из i(24) получаем i?2=2,81 кОм, =265,26 кОм и J?7=5 кОм. Для того чтобы получить k=0, выберем Rs=Rfi=lO кОм и заземлим конец резистора Re, который присоединен к зажиму Il. На рис. 5.7-6 показана частотная характеристика это-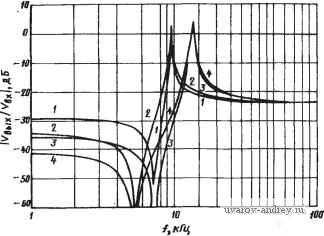

Рис. 5.7-6. Частотная характеристика фильтра в примере

5.7-2

го фильтра и демонстрируется процесс его настройки. Кривая / соответствует номинальному фильтру. Кривая 2 соответствует сопротивлению i?7=9 кЦм, чтобы показать его влияиие на cOz. На кривой 3 (где значение восстановлено до своей первоначальной величины - 5 кОм) иаменено до 1,3 кОм, Jto-бы настроить coj,. Наконец, кривая 4 показывает результат иопользовяния i?2=l,3 кОм и i?7=9 кОм для настройки KaiK coj так и Шг.

При вычислении характеристик этого фильтра следует иметь в виду,/ что схема исходного резонаторного фильтра стала бы неустойчивой при fp>GB/4Qj,o=2,5 кГц (полагаем, что GB=500). Улучшение характер.5стик схемы за счет модификации демонстрирует рис. 5.7-7. На рис. 5.7-7,а процентное изменение Qp вычерчивается в зависимости от температуры KaiK для

а 10 20 30 w so 60 70 en so m

n] T,C

J 7 .) Z

6] V -

I I 1 1 M I

jr s 7 ,ia

Puc. 5.7-7. Относительные изменения характеристик добротности фильтров в

примере 5.7-2:

1 - нормальный; 2 - модифицированный резонатор

исходного, так и для модифицированного варианта резонатора. Изменение Qp для модифицированного варианта составляет около 5% ири -изменении температуры более, чем на 60°, тогда как для исходного варианта оно равно приблизительно 130% в том же самом температурном диапазоне. Другая характеристика этого фильтра показана на рис. 5.7-7,6. Заметим, что здесь процентные отклонения фактического Q от желаемого, выраженные как функция fp, меньше, чем -2% для значений fp, изменяющихся от 1 до 30 кГц.

Одним из недостатков модифицированной резонаторной схемы, показанной на рис. 5.7-5, является то, что она требует более точной компенсации частотной зависимости параметров усилителей, чем исходная. Причину этого можно понять, если рассмотреть петлю обратной связи, состоящую из усилителей Лг и Лз. Ни один из этих усилителей не имеет в цепи собственной обратной связи конденсаторов, следовательно, не существует ко-роткозамкнутого пути для высокочастотных составляющих. В результате этого запаздывание по фазе усилителей на частотах, близких к GB, может создать значительный фазовый сдвиг, который может вызвать генерацию на высоких частотах. Как правило, частота колебаний численно равна GB, а амплитуда определяется усилителем. Часто высокочастотная генерация не искажает работу усилителя и даже может не быть заметна на выходе фильтра (благодаря демпфирующему действию конденсатора Сг). На практике, однако, характеристику усилителя на высоких час-

тотах следует тщательно контролировать, чтобы быть уверенным, :то высокочастотная генерация отсутствует. На рис. 5.7-5 пункти-)0М показаны элементы, используемые для того, чтобы исключить такую генерацию.

В заключение рассмотрим неустойчивый режим работы моди-Ьцированного резонаторного фильтра, который возможен при больших значениях Qp и fp и который обычно вызван фазовым сдвигом из-за конечной скорости нарастания выходного сигнала ((:м. § 5.4). Если уровни сигнала в схеме становятся достаточно б)льшими, то схема переходит в неустойчивый режим. Такой вид неустойчивости можно устранить подключением параллельно входам усилителей Л2 и/или Лз двух встречно-параллельно включенных кремниевых диодов, которые ограничивают входные сигналы удилителя до значения ±Vd, где Vd - падение напряжения на диоде в прямом направлении.

I Концепцию внутренней компенсации усилителей можно также применить к схемам основанным на методе переменных состояния. Метод с помощью которого можно достичь этого, иллюстрирует рис. 5.7-8,а. Если выходы усилителей Лг и Лз поменять местами.

/?г

г-il-i

1 v -о о-о-

-о

Рис. 5.7-5. Модификация фильтра, сформированного по .методу переменных состояния, для обеспечения собственной компенсации усилителей

ТО схема примет вид, показанный на рис. 5.7-8,6. Здесь полярность подключения усилителя Л 2 изменена на противоположную для обеспечения устойчивости. Аналогично тому, как это было сделано для модифицированной резонаторной схемы, можно получить соотношения, показывающие, что произведение коэффициента усиления на ширину полосы операционного усилителя можно исключить из выражения для добротности Qp. Соответствующий пример приведен в задачах к данной главе. Модифицированная схема фильтра, основанного на методе переменных состояния, требует включения обозначенных пунктиром элементов (см. рис. 5.7-8,6) для предотвращения высокочастотной генерации, которая может возникать, как было указано выше. Кроме того, может потребоваться пара кремниевых диодов, включенных параллельно входам усили-

телей Лг и Лз, для предотвращения неустойчивой работы схемь| из-за превышения допустимого уровня входных сигналов, когда Qp и /р велики.

До сих пор в этом параграфе мы рассматривали минимизацию чувствительности Scb- Часто оказывается важно также минимизировать чувствительности S<nQs и/или З^гов- Из них mi-нимизация Sn gb обычно не так важна, потому что большое зйа-чение этой чувствительности еще не означает, что фильтр будет неустойчив - это более вероятно, когда велико значение Sb.

SPi gb\ приводит 0д1

Конечно, минимизация чувствительности

временно к минимизации Sgb и S ugb. Достичь этого, используя только эффекты первого порядка, вполне возможно (см. задачи в конце главы), но техника подобного рода нуждается в усовершенствовании, чтобы ею можно было пользоваться в общем случае.

5.8. Выводы

В этой главе были рассмотрены несколько типов усилительных ?C-фильтpoв. В § 5.1 было показано, как один операционный усилитель можно использовать в схемах с многопетлевой и однопетлевой обратной связью для реализации большинства широко используемых фильтров. В § 5.2 были рассмотрены хорошо известные схемы резонаторных и основанных на переменных состоя-

Таблица 5.8-1 Сравнение различных типов ?С-фильтров на усилителях

Тип i?C-фильтра

Малое число пассивных элементов

Малое число активных эле.чеитов

Малый

номиналов элементов

Простые расчетные соотношения

Низкая чувствительность

Реализует высокие добротности

На одном усилителе с положительным коэффициентом усиления (§ 4.2 и 4.3) На одном усилителе с бесконечным усилением и многопетлевой обратной связью (§ 5.1)

На одном усилителе с бесконечным усилением и однопетлевой обратной связью (§ 5.1) Со многими усилителями на основе переменных состояния

(§ 5.2 и 5.3) Резонаторный, со многими усилителями

<§ 5.2),

шя фильтров со многими усилителями. Обе эти схемы хорошо юдходят для реализации высокодобротных функций. В § 5.3 ис-едовалась модификация фильтра, основанного на переменных 1ЯНИЯ, названная универсальным активным фильтром. В 5.4 детально исследовались свойства интегратора, использованного в фильтрах на основе переменных состояния и резонатор-ншх фильтрах. В § 5.5 было показано, как неидеальные свойства операционных усилителей приводят к эффекту увеличения доб-роггности для указанных типов фильтров. В § 5.6 обсуждаются общие последствия ограничений на произведение коэффициента ус!ления на ширину полосы операционных усилителей в различных фильтровых реализациях. Наконец, в § 5.7 был исследован вариант резонатора, который не зависит от произведения коэффициента усиления на ширину полосы. Обзор свойств различных схем 7?С-фильтров на усилителях, рассмотренных в этой и предыдущей главах, приведен в табл. 5.8-1. В этой таблице знак указывает, что качество данного фильтра по указанному параметру выше среднего, тогда как знак i - указывает, что качество фильтра в этом плане среднее или ниже среднего.

5-1 (§ 5.1). Используя схему многопетлевого фильтра на одном усилителе с бесконечным усилением, показанную на рис. 5.1-2, реализуйте бессе-леву функцию нижних частот второго порядка с ГВП 500 мкс я единмным коэффициентом передачи на постоянном токе. {Указание: выберите С= =0,05-10-* Ф, т=\14 и используйте меньшее из двух возможных значений

для Я2.)

5-2 i(§ 5.1). а) Для ФНЧ на одном усилителе с .бесконечным усилением и миогопетлевой обратной связью, схема которого даиа на .рис. 5.1-2, полагая i?i=/?2=tR3==/?, найдите выражения для величин Ши, l/Q и Яо из (1), § 4.2.

б) Иопользуя эти величины, найдите выражения для R и Се Полагайте, что Сб принимает удобные для использования значения.

в) Иопользуя указанные соотношения, найденные вьш1е, синтезируйте фильтр, удовлетворяющий специф.икации, данной в примере 5.1-1.

5-3 (§ 5.1). а) Синтезируйте ПФ с шириной полосы на уровне -3 дБ от 725 до 800 Гц и коэффициентом усиления на резонансной частоте О дБ. Используйте ФНЧ-ПФпpeolбpaзoвaниe соответствующей двухполюсной функции Баттерворта для нахождения полосовой передаточной .функции. Используйте полосовую структуру с многопетлевой обратной ювязью .на одном усилителе с бесконечным усилением, показанную на рис. 5.1-4, для реализации пары полюсов полосовой передаточной функции.

б) Повторите задачу, полагая, что коэффициент усиления на резонансной частоте должен быть равен 20 дБ.

5-4 (§ 5.1). Другую полосовую структуру фильтра с многопетлевон обратной связью на одном усилителе с бесконечным усилением можно реализовать, полагая Yi=sCi и Ys=Gi в схеме на рис. 5.1-1. Определите для да.н-иого выбора другие элементы, найдите передаточную функцию и разработай-