Заметим, что аир - вещественная и мнимая составляющие комплексных полюсов соответственно. Решая (21) относительно ¥2(5) и полагая, что на вход подана ступенчатая функция, получаем

VAs)Nis)/s[is+aY-\-n (23)

Проводя обратное преобразование Лапласа и определяя 12(0 = =2~[V2{s)], находим, что переходный процесс описывается выражением

£;,(0 = /Ci-fK2e- sin(p + 9), (24)

где величины Ki, /Сг и ф зависят от полинома N{s). Общий вид {t) представлен на рис. 5.5-3, где не показана форма колебаний при /=0, так как ф - произвольная величина. Значение а можно найти путем измерения интервала времени Ti между любыми двумя точками на огибающей, в которых амплитуда равна А и Л/е=Л/2,7183 (е - основание натурального логарифма) соответственно, как по- казано на рис. 5.5-3. Численное значение р можно найти путем измерения интервала времени Т2 между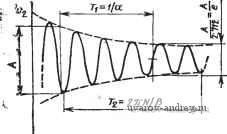

Рис. 5.5-3. Определение добротности высокодобротного фильтра

N минимальными или максимальными амплитудными значениями на характеристике. Следовательно,

а = 1/7-1; р = 2яВД. (25)

Из (22) следует,

Q = VlRV2a; (oViF+. (26)

Так как для высокодобротных схем переходный процесс, показанный на рис. 5.5-3, затухает очень быстро, то для практики этот метод измерения (й„ и Q очень удобен.

5.6. Частотно-зависимая чувствительность

В этом параграфе рассмотрим свойства реализаций фильтров, представленных в данной главе, в диапазоне частот, как следствие чувствительности их полюсов к изменению величины GB. Эти свойства реализации фильтра с бесконечно большим коэффициентом усиления можно проанализировать так же, как это сделано для фильтра с конечным коэффициентом усиления в § 4.7. В этом случае Оа [см. (20), § 4.7] равно 1/Ло 0. Подставляя выражения для полных проводимостей К из § 5.1 (для реализации фильтра ниж-

них частот с бесконечным коэффициентом усиления) в {П\, § 4.7, (gi=Ci, 1=0, 1,2), получаем

6а = СвСв; bi = Ce(Gi + Gs + Gs): К=0Сз\ (1а)

: 92==СеСв; 9i = Ce(Gi-(-G2 + G3) + GsCe; qGG + GG. (16) Для этого фильтра

(l = bo/b = bo/q; (aJQ=bJb = b,/q: (2а). (26)

1о2 Яо = Gi Gs/&2 = Gi Gs/92. (2в)

Из (16) видно, что qi = bi + G3C5 и 9о = 6о + С,Сз. Подставляя эти выражения в (2), получаем

o> = 9o/9a-Gi;G3/9i; co /Q = 9i/92-GsCe/a. (За), (36) Следовательно, л: и у из (Ю), § 4.7, примут вид

Х= -GsCbQ/co = -2 Q/JRa Ge = -9а Q VR Сь/з С ; (4а)

y = q-

(46)

Подстановка их в (16), § 4.7, дает

GB 1/4 да-1

I /%Сбу/2

Одна из процедур синтеза, используемая для реализации ФНЧ с бесконечно большим коэффициентом усиления, состоит в выборе равных номиналов сопротивлений, т. е. /?,=/?2=/?з=- При этом (5) приводится к виду

Is. =

GBy4Q -l [ С, Q

Для такой процедуры синтеза добротность

/ С у/2 I С, /

(7) (8)

(г=1/Св/Св/з.

Объединяя (7) с (6), получаем

So41 = (Q >n/G5 VW) (9Q2-2)/2.

Знаменатель третьего порядка передаточной функции для этого фильтра принимает теперь вид|

= qyiGB+sM I + (OJGBQ + {(oJG В) (R ClR С^)Ч^ ] +

+ 8К/(г + (ш2+й)2Я„)/ОВ1+ш2}. (9)

Преобразуя это выражение и полагая, что используется процедура с выбором равных номиналов сопротивлений, получаем

D (*) = (qGB) [s3 + s2 (GS+ojQ+3 Q со J+s (й) G5/Q+2fi)+GJ3].

Нормируя результат на имеем

D (s ) = -[s3 + (GB + l/Q + 3Q)s+(GB /Q+2)s + GB l. (il>

Местоположение комплексных полюсов, лежащих в верхней полуплоскости, в зависимости от величины GBn для рассмотренного полинома знаменателя с Q в качестве параметра показано на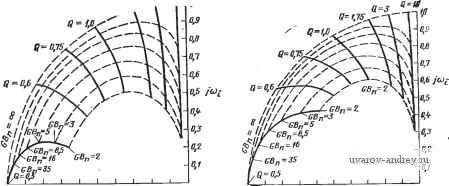

-iO-0,9 -0.8 -€,7 -Цб -0,5 -fl> -0,3-0,1-0,1 О

Рис. 5.6-1. Влияние GB на положение полюсов С-фильтра нижних частот второго .порядка на одном усилителе с бесконечно больпшм коэффициентом усиления (см. § 5.1)

1,0 ofl Ofi 0,7 0,6 Ofi 0,6 0,3 а,г o,i а <!i

Рис. 5.6-2. Влияние GB на положение полюсов ПФ второго порядка на одном усилителе с бесконечно большим коэффициентом усиления (см. § 5.1)

рис. 5.6-1. Сравнивая полученное с рис. 4.7-2, можно видеть, что реализации с конечным и бесконечно большим коэффициентами усиления имеют аналогичные зависимости от GB. Реализации ФВЧ и ПФ схемами с бесконечным усилением можно проанализировать так же, как это сделано выше. Результаты такого анализа сведены в табл. 5.6-1. Соответствующие зависимости положения комплексных полюсов, лежащих в верхней полуплоскости, от . величины GBn и Q в качестве параметра показаны на рис. 5.6-2 и 5.6-3.

Q=D,7S

Q = B,6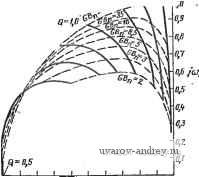

-Sft-ofi-Bfi -oj -o.-ofi-B,t-a,3-o,z-a,i

Puc. 5.6-3. Влияние GB на положение ФВЧ второго порядка на одном усилителе с бесконечно большим коэффициентом уоиления (см. § 5.1)

Частотно-зависимые чувствительности для реализаций фильтров с бесконечно большим коэффициентом усиления

Реализация

Ограничение

Нет

ФНЧ

(рис. 5.1-2)

(рис. 5.6-(1)

Ra Съ

D{sn)

( + 2)s -bGB

(рис. 5.1-4)

Нет

С2 = Сз = С

(рис. 6.6-2)

5Й| =

GBV4Q2

si -l-(GB +--b2Q)s2 +

+ GBn

Нет

ФВЧ

(рис. 5.1-5)

(рис. 5.6-3)

GBV4Q2 i

Re Gs

Яо fR,Csy/2 Q W

L5 Gz 1/2

C(s ) =

g2 0 n

Xsl+[+l)sn + GBn

Пример 5.6-1. Фактические значения cin и Q полосового фильтра с бесконечно большим усилением. Требуется реализовать ПФ второго порядка с Q=8,53, if = 1000 Гц, Hq-1, иопользуя процедуру синтеза с емкостями равных номиналов. Произведение коэффициента усиления на ширину полосы для усилителя равно 1 МГц. Фактическое положение полюсов можно найти, используя реализацию (13), § 5.1, и принимая С2=Сз=С=0,01 мкФ. В результате получаем /?i=135,8 кОм, ./?б=939 Ом и J?6=271,6 кОм. Желаемое положение (Комплексных полюсов можно айти из выражения Pi,2=<0n/2QX Х(-1±]4<Э^-!) Следовательно, pi,2=-368,8±j6272. Фактическое положение полюсов можно вычислить с помощью (И), § 4.7, иопользуя GB = 1000. Так как в соответствии с (10), § 4.7, для реализации ПФ с беоконечным ко-

вффициентом усиления с С2=Сз, у=0 и x-qQ, то вещественные и мни 11ые части полюсов можно найти из соотношений

Re I6pi/aGB] = -1/02 = 10в; (12а>

Imjapf/aGB] = (2Q2 1)/gb2 Qy4Q2 1 = 0,99.10-* lO -*. (126)

Вещественные и мнимые части вариаций положения полюсов за счет изменения GB можно найти путем домножения на dGB, т. е.

Re [dpf] Re [dpt/dGB] dGB = 2п; (I3aJ

Im [dpt] w Im [dPi/d GB] dGB = -2n. (1Щ

В этом случае dGB представляет собой изменение GB от оо до 1 МГц; следовательно GBdGB<iO. Фактические положения полюсов теперь таковы; Pi,2=-361dbj6266. Фактические fn и Q, обозначенные как fn** и дФакт^ вычисленные с учетом фактического положения полюсов, равны: факт=998,9 Гц и СФа =8,67. <ф

Последняя категория jRC-фильтров, которая будет рассмотрена в этом параграфе, - фильтры с использованием нескольких усилителей. Эта категория включает в себя фильтры, реализованные по методу переменных состояния, и резонаторные фильтры, введенные в § 5.2. Сначала рассмотрим реализацию фильтра на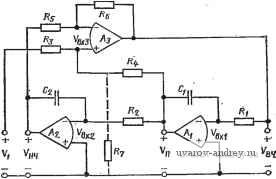

Рис. 5.6-i. Схема фильтра, реализованного по методу переменных

состояния ;

основе переменных состояния (рис. 5.6-4). Выражение для Vbi3.(s), определенного на рисунке, можно записать в виде

Определим теперь передаточные функции

-= Vn (s)/Fb4 (s); 4 (s) = l/нч isW (s);

4(*)-1b4(s)/Fbxs(s). (15)

- Решая эти уравнения относительно У^ч {s)/Vi{s), получаем

i+() + .()A()+A(s)A(s)(s);

.f (16)

Знаменатель этой передаточной функции будет одинаков для случаев ФНЧ и ПФ, как инвертирующей, так и неинвертирующей жонфигураций. Его можно записать в виде

D(s) =-?-+-!---+

Л (S) Л is) А is) Ai is) л is) /?5 + .

1 Ra , R>

Asis) Rs + Ri Rb + R, Используя (3), § 5.4, можно записать:

(17)

A-is) - fl: A,is)--=f (18)

s (s + wi + GBi) s (s + CO, + GBa)

!Где a)i = l/J?iCb 0)2=1/22 и cuo<cGB. Так как Лз(5) в выражении (15) дает коэффициент усиления операционного усилителя Лз при .разомкнутой петле обратной связи (рис. 5.6-4), то его можно вы-ipasHTb как

Asis)fifGBs/3. (19)

Объединяя приведенные выше результаты, получаем следующий полином пятого порядка для D (s):

+(-5) [?±(+ .+ и.+ >.и.)]1: (20)

можно показать, что .

cu2 = a)iCuai?e/5; (21а)

) /Q=[(1+ад)/(1 + ад+RJRt)] 1. (216)

Резистор Ri, введенный в схему фильтра, основанного на переменных состояния, как показано на рис. 5.6-4 (см. также схему универсального активного фильтра на рис. 5.2- 1) влияет только яа величину con/Q, приведенную в (216). Если Rj отсутствует в схеме, то, подставляя R7=oo в (216) и пренебрегая членами (s/GB)2 и is/GB) в выражении (20), получаем упрощенное выражение для D(s):

D is) (s + а) slQ+со2) + (s/GB) [(3 + RM +

-f(c0i + (fla + a)jQ)s + C02a) /Q]. (22)

Сравнивая его с (6), § 4.7, можно получить следующие соответствия:

А:=1; g2 = 3 + RjR; 9 = со + coj + cu /Q; goaajta. (23) Подставляя эти величины в (10), § 4.7, получаем

x = 2 + R,/R-(Q/VrJr,) {Уё+ ); (24а>

y = 3 + RR-l/Q{VefVRjR;), (246)

где 8 = cu2/b)i- (25)

Типичными расчетными значениями для реализаций по методу переменных состояния являются: Re/R5=l/10 и е=1. Следовательно, вместо (24) получаем

x=2,i~VQ; y3,l~VT0/Q. (26).

Полагая, что Q>1, находим х^-6,32 и ул3,1. Подставляя эти величины в (16), § 4.7, имеем

IWnQ/GBVWl.

(27>

Сравнивая этот результат с результатом, полученным для реализаций с одним усилителем, видим, что фильтр на основе переменных состояния похож на фильтры с положительным коэффициентом усиления в отношении его зависимости от произведения коэффициента усиления на полосу пропускания. График изменения положения комплексных полюсов в верхней полуплоскости можно-получить из (22) путем нормирования относительно соп; в результате

+ Sn{GBjQ+(oM+GBn

(28)

где a)iTi= )i/a) и a)2n==cu2/ )n- Годограф, получевный из этого уравнения, показан на рис. 5.6-5. Как видно из рисунка, полюсы реализации фильтра на основе переменных состояния могут оказаться в правой полуплоскости для больших значений добротности (на рис. часть оси jo представлена в большем масштабе, чтобы лучше видеть детали). Так как у фильтра на основе переменных состояния передаточная функция при разомкнутой цепи обратной связи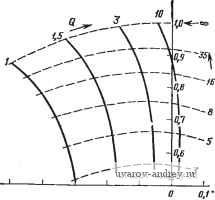

-0 -0,4 -0,3 -0,2 -0,i

Рис. 5.6-5. Влияние GB на положение п-олюоов фильтра, реализованного по методу переменных состояния

Is точке ып приблизительно равна 1Z.0°, то небольшое по величине 1 запаздывание по фазе, вносимое интеграторами и сумматором, вызовет эффект увеличения добротности. Это тем более верно для юольших значений ( .

\ Рассмотрим теперь резонаторную реализацию, схема которой юказана на рис. 5.1-4. Для этой реализации

(S) = - (s) V,, (s) = ~А (s) ( fl ] Vi (s) -

wm ( i = i/i?iCi; Ki+RiJRi+Ri/Rs, (Щ

Adi является коэффициентом усиления операционного усилителя Ai при разомкнутой петле обратной связи. С помощью рисунка можно определить

I A,{s} = V,{s)/V(sy, Л(5)=1/нч(5)Жп(8). (31)

Подставляя эти выражения в (29), находим

Уп() -AdAs)ai{Ri/Rd/{s + K(Oi)

Д + Adi (S)\ , +Лй(.5)Л(5)Л( )----

(32)

s + Кщ

Знаменатель этой передаточной функции можно записать в виде

Л (S) = (S -Ь K(d/Adi (S) (S) А, (S) + {s + c0i)M2 (s) А, (s) + со RjR. (33) Подставляя соотношения

Adi(s) i-GBJs; (34а)

(s) -GB/s (s -Ь + СБа); (346)

Лд (S) (- 0Вз/2)/(8 -Ь сад (34в)

ш полученное выше выражение, имеем D (S) = (s+S/Q + со2) -Ь (8/СБ) [4s2 + (Зю -Ь со + со /Q s -Ь со ш^Ц--Ь (s/GB)2 [5s2 + (2 i + Зсо, -}- 3 )j /О s -Ь (2 со со -Ь со со К)] +

+ (s/GBf [2s2 + (2 + 2(Bi /С) s -Ь 2 1 со], (35)

откуда следует, что

= 1 21/3; )n/Q = i; /C=i+i?i ?4+i/3; (36а)

cui=l/i?iCi; cU2=l/i?2C2. (366)

Пренебрегая членами (s/GB) и (s/GB) в (35), получаем .£) (S) = (s + и„ S/Q + и2) + (S/GB) [4s2 + (и, + Зю -Ь /Q s -Ь ш^]. (37)

Действуя далее, как и в случае реализаций на основе перемен-лых состояния, получаем

ft=l; , = 4; , = (o, + (o,4+--b-j; % = C0i(0,. (38)

Решение для х я у, определенных в (Ю), § 4.7, дает

х= -QR3/Ri-RjjR3-Ri/Ri= -4h/(-Q/(<oM-Ri/Ri; (39а>

у = A-RlRi = 4-©2/0)2. (39

Полагая, (Bi=<B2 и RilRt=H(, (ПФ), получаем

х=-\ -Q-Яо (40а>

i/ = 4-l/©2ft;4 (406)

для Qp>\. Следовательно, модуль чувствительности полюса

(4l>

Из результатов, полученных выше, видно, что характеристика-резонаторного фильтра для Qp>\ аналогична характеристике реализации фильтра на одном усилителе с бесконечно большим коэффициентом усиления. График изменения местоположения комплексных полюсов в верхней полуплоскости можно получить из (37> путем нормирования на ( -

GBn L

4s3 + si (GBn + гп + 2 + ©i К) +

GBn Q

(42)

где cuin=©i/cun и cu2n = ©2/©n. Результирующий годограф как функция GBn с Q в качестве параметра показан на рис. 5.6-6. При вы-

черчивании графика предполагалось, что cuin=l/Q, cu2n = l и К=

-=l + Q+Ri/R4. Это соответ-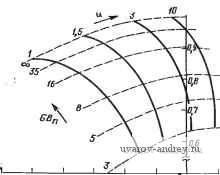

ствует процедуре синтеза^ данной в § 5.2. Можно видеть, что недостатком реализаций с бесконечным коэффициентом усиления является то, что корни могут оказаться в правой полуплоскости jco при больших значениях GBn. Сравнивая фильтр на основе переменных состояния с резонатор* ным фильтром, при условии, что процедуры синтеза одинаковы, можно сделать вывод, что первый из-них имеет больший запас устойчивости.

В этом параграфе исследовалось влияние частотной зависимости параметров усилителя на различные типы реализаций фильтров, которая характеризуется величиной \8Ргсв Если множитель {(OnlGB)/ ]/4Q2-1 исключить из формулы для чувствительности

-Ofi -0,5 -o,it -0,3 -о,г

Рис. 5.6-6. Влияиие GB на положение полюсов .резонаторного фильтра

которая здесь вычислялась, и если Qp>l, то можно провести сравнение чувствительностей различных реализаций. Предполагается, что величина Но приблизительно равна единице. Для реализаций на основе переменных состояния и положительного коэффициента усиления 5РгоБ не зависит от Q. Для резонаторной реализации и бесконечно большого коэффициента усиления Sp.gb пропорционален Q. Аналогичное исследование свойств реализаций с отрицательным коэффициентом усиления показывает, что 5оБ* .пропорционален Это еще одна причина непопулярности таких реализаций.

Вопросы, рассмотренные в этом параграфе, имеют большое значение в практике активных фильтров. Непосредственное использование результатов, полученных в нем, заключается в том, что-1бы учесть в процедуре синтеза величину произведения GBn- Если сй . и Q известны и известна GB, то сдвиг полюсов можно вы-числить либо с помощью графиков корневых годографов, либо с помощью выражения (8), § 4.7. Компенсированное положение по-люсов получается тогда путем добавления сдвига полюсов к желаемому положению полюсов. Знание компенсированных положений полюсов позволяет определить компенсированные значения to и Q, которые могут затем использоваться в качестве технических требований нормальной процедуры синтеза. Успешность такого подхода основана на предположении, что сдвиг полюсов линеен в окрестности желаемого положения полюса. Так, в примере 5.6-1 компенсированное положение полюсов может быть вычислено как р1,2=-375,1 ±j 6278,3, что согласуется с компенсированными значениями fn и Q, равными соответственно 1001 и 8,36. Хотя такая процедура не может обеспечить точной компенсации, тем не менее она позволяет значительно снизить влияние GB усилителя на синтезируемую реализацию и позволяет легко подстроить ее. Результаты, полученные в этом параграфе, позволяют также выделить такой тип реализации, который соответствует заданному набору технических требований. Кроме того, они могут использоваться для определения требуемых характеристик усилителей, необходимых для удовлетворения различных технических требований. Наконец, эти результаты дают ту основу, которая необходима для поиска реализаций, имеющих улучшенные частотные характеристики.

5.7. Реализации, не зависимые от произведения GB

Для того чтобы получить одновременно и хорошую характеристику в области высоких частот и большую добротность активного фильтра, важно минимизировать чувствительность ISioB] фильтра относительно произведения коэффициента усиления на ширину полосы. В этом параграфе покажем, как это можно сделать, используя .методы компенсации. Такие методы применимы, прежде всего, к тем схемам фильтров, у которых заземлен один из входных зажимов, так как в противном случае частотная характерно-