чение (Urc, однако, сохраняется постоянным и составляет 500 крад/с. Из приведенных кривых видно, что влияние выходного полного сопротивления уменьшается с уменьшением С, т. е. емкость нагрузки должна быть как можно меньше.

Запаздывание по фазе, обусловленное ограничением на значение GB операционного усилителя, может быть достаточно велико, что требует специальной компенсации. Один из методов осуществления этого состоит во включении небольшого сопротивления Rj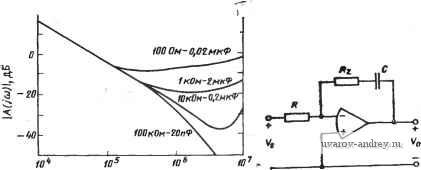

Частота, Гц

Рис. 5.4-4. Частотная характеристика реального инвертирующего интегратора

Рис. 5.4-5. Компенсация вапазды-вания по фазе для инвертирующего интегратора

последовательно с емкостью С, как показано в схеме на рис. 5.4- S. Это создает полюс функции в цепи обратной связи, что приводит к появлению соответствующего полюса в передаточной функции интегратора в целом. Анализируя схему на рис. 5.4-5, получаем передаточную функцию вида

-GB[s(Rz/R) + a>j,c] (13)

Vois)

Vs(s) S + (Oa + 0iic + GB)s + (x)ifca

где принимается Rz<R. Заметим, что знаменатели (13) и (3) идентичны, однако в числителе (13) появляется нуль, расположенный в точке (siz=\IRzC. Фазовый сдвиг (13) можно аппроксимировать выражением вида

arg [АЦа)]п + arctg (со/©,)-arctg [со GB/(u) corc-и^)] . (14)

Полагая, что соаСОдс-Ссо^, получаем

arg [А (]©)]? я/2 -i- co/co-co/GB. (15)

Таким образом, если (dz=GB, то запаздывание по фазе, вызванное конечным значением GB, устраняется и не возникает до тех пор, пока не начнут сказываться эффекты более высокого порядка. В качестве примера можно привести результаты, приведенные на рис. 5.4-6. В этом примере GB=1 МГц, R=200 кОм и G=20 пФ. Один из недостатков данного метода компенсации с ис-яользованием Rz состоит в том, что результат компенсации зави-

сит от соблюдения условия u)z=G5. Вероятно, температурные коэффициенты сог и GB неодинаковы, следовательно, компенсация полученная данным методом, будет зависеть от температуры. Другой недостаток данного метода заключается в том, что GB меняется в зависимости от конкретного операционного усилителя. В результате каждый операционный усилитель должен быть компенсирован в отдельности.

argA(jai)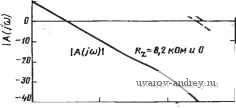

/о* to

Частота, Ги.

tss 90

Э

Г о ч:

о

--Яв -435

Рис. 5.4-6. Частотная характеристика компенсированного инвертирующего .интегратора

Второй метод компенсации запаздывания по фазе показан н.21 рис. 5.4-7. Здесь дополнительная емкость Ст включается параллельно сопротивлению R. Анализ этой схемы дает:

A{s):

Vo(s)

<rc GB

S-l- Mz

(16)

где ft)a~0 и fx)z=i/RCz- Для получения желаемой компенсации отрицательные вещественные полюс и нуль в этом выражении должны сокращаться. Таким образом, требуется, чтобы

©,=GB. (17>

В этом случае, если СБ>(йнс, то (16) определяет передаточную функцию идеального инвертирующего интегратора. Очевидно что недостаток, обусловленный необходимостью выполнения условия m=GB, описанный выше, присущ и этому методу компенсации.

Третий метод компенсации запаздывания по фазе, вносимого-инвертирующим интегратором, состоит в использовании еще одного операционного усилителя. Этот метод иллюстрирует рис. 5.4-бе-Усилитель с единичным коэффициентом усиления включен как буфер в цепь обратной связи инвертирующего интегратора. Передаточная функция этой схемы

(1 -f (S)) [ СОдс/(-Ь COj;c)]

Л(5) =

Yo{s)

V, (S) 1 /(S) + 1 /Лй, (S) (S) -I- S/ (S -I- Orc)

(18)

где Л^1(я) -коэффициент усиления усилителя Ai при разомкнутой цепи обратной связи и Ad2 - аналогичный коэффициент усиления усилителя Лг- Используя однополюсную модель для усилителей этой схемы, получаем

Vois)

Vs(s)

-cocGS, (S-I-GS2)

s [s + (GS2 -I- Шдс) s + (Иде GB2 + GBi GB2) + <Ofli GBi/s]

(19)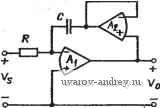

Puc. 5.4-7. Компенсация запаэдывания по фазе инвертирующего интегратора

Рис. 5.4-8. Использование операционного усилителя для компенсации запаздывания по фазе инвертирующего интегратора

Фазочастотную характеристику (19) можно записать в виде

arg [Л (]©)] = п/2-f-arctg (©/GBa)-

-arctg (cu/GBi + fflcoc/GBijBa-WRCtOai/wGBa), : (20)

где принято GBiGB2><i) и GB\><iiRc. Принимая во внимание то, что аргументы функций арктангенса в (20) малы, можно упростить (20):

rg И (j и)] fa n/2+<i)/GB-a/GBi~(ixoiic/GBi GS+cuKcb)ai/ Ga- (21)

Сравнивая этот результат с (7), видим, что буфер в цепи обратной связи внес опережение по фазе, которое можно использовать для устранения запаздывания по фазе, вносимого интегратором. Если 1С0 = <Влс, GBi = GB, Лог = Ло, (йаг = <йа, ТО

arg [Л (j щс)] л/2-{anc/GBf + содс/© Л^. (22)

Рассмотрим теперь реализацию инвертирующего интегратора. Один из подходов состоит в каскадном соединении интегратора и инвертора, как показано на рис. 5.4-9. Фазочастотная характеристика этой схемы

arg [Л (] ю)] -л/2-a/GBi-2 w/GB. (23)

При наличии согласованных усилителей характеристика принимает вид

arg [Л (]©)] #-п/2-3C0/G5. (24)

Из этого выражения следует, что схема на рис. 5.4-9 в общем случае неудовлетворительна из-за значительного запаздывания по фазе.

Схема другого неинвертирующего интегратора показана на рис. 5.4-10. В этой схеме инвертор помещен в цепь обратной связи инвертирующего интегратора для того, чтобы, во-первых, сформировать инвертирующий вариант интегратора, во-вторых, обеспе-

Рис. 5.4-9. Реализация неинверти- Рис. 5.4-10. Иопользование опера-рующего интегратора . ционного усилителя для компенсации

запаздывания по фазе в неинверти-рующем интеграторе

чить опережение по фазе, используемое для компенсации запаздывания по фазе, вносимое инвертирующим интегратором. Заметим, что для получения отрицательной обратной связи провод обратной связи должен подключаться к зажиму -Ь усилителя Ль Анализ pifc. 5.4-10 дает следующую передаточную функцию:

Vojs) Vs{s)

<ncilAdAs) + Rd{Ri+ R2)\

A{s).

(25)

Ri + Ri

Adi (s) (s) Aai (s) {Ri + i?)] Подставляя модель с доминирующим полюсом для Ad\{s) и A.d%{s), получаем

... о>р,с GBi [S + GB RiURi + R)]

A{s):

с

GB,+ t;GB,GB,+.

Ri+R

R1+R2

(26)

где принято, что (аа<.ОВ. Фазочастотная характеристика для А argH(i ] -f-farctg(--)-

{GBGBa R2 + GB2R2 iuAnR2 )

где (i\<.GBi (или GB2) и clibc<GBi. Если аргументы функций арктангенса малы и GBi = GB2=GB, то (27) можно переписать в виде

arg {А (з О))] л;-jt/2 + (й/GB + RClAoi-2 (fdiGBf s - л/2 + ш/СВ. (28)

Таким образом, указанный инвертирующий интегратор имеет избыточное опережение по фазе, приблизительно пролорциональ-ное (й/GB. Вследствие этого данная схема может быть полезна для устранения запаздывания по фазе, вызванного обычным инвертирующим интегратором (см. рис. 5.4-1), в цепях обратных связей которого содержатся оба типа интеграторов [54].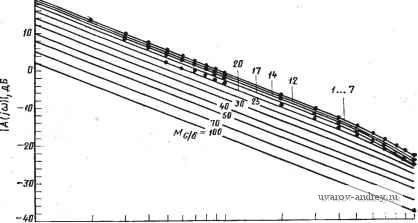

0,01 0,0Z 0,03 0,Dt 0,05 0,07 0,1 0,Z

gjleb

0,3 0,f 0,5 0,1 1,0

o,m B,az 0,03 o,af o,os 0,07 0,1 ofl. 0,3 o,-, 0,5 d,i 1,0

gjIgb S)

Puc. 5.4-11. Искажения в инвертирующем интеграторе в режиме боль-. . шого сигнала

Последнее, что рассмотрим в связи с инвертирующим интегра-Э'ором, это искажения в режиме большого сигнала, вызванные ограничениями на скорость нарастания выходного сигнала. Чтобы убедиться в их наличии, представим сначала выражение для фазочастотной характеристики в виде

arg [А (] О))] = я/2-arctg {1/[1 + (СВ/ш) N (Л)]}, (29)

где N{A) является описывающей функцией системы. Равенство N{A) = [ соответствует отсутствию искажений в режиме большого сигнала, тогда как неравенство N(A)<il соответствует искаже- иям, вызванным указанными выше причинами. Если N(A) устремить к нулю, то можно заметить, что результаты, полученные при этом в (29) и (10), § 4.6, отличаются, а именно: инвертирующий интегратор более устойчив к искажениям в режиме большого сигнала, чем инвертирующий усилитель. Влияние искажений в режиме большого сигнала на частотные характеристики инвертирующего интегратора иллюстрирует рис. 5.4-И для (йдс = СВ/10. Величина Mg является амплитудой входного сигнала, а б - пороговым уровнем (см. рис. Б-13 в приложении Б). Результаты, приведенные выше, соответствуют инвертирующему интегратору. Аналогично можно провести исследование неинвертирующего интегратора. Однако, так как ограничения на скорость нарастания выходного сигнала создают запаздывание по фазе, а данный неинвертирующий интегратор создает опережение по фазе, можно предположить, что его характеристики в режиме малого сигнала будут меняться в меньшей степени, чем у инвертирующего интегратора.

5.5. Эффект увеличения добротности

Когда схемы, основанные на методе переменных состояния, или резонаторные схемы, описанные в § 5.2 и 5.3, используют для реализации высокодобротных функций фильтрации, то оказывается, что полученные добротности обычно выше тех, которые ищут в соответствии с процедурой синтеза. Это явление носит название эффекта увеличения добротности. Он вызван, главным образом, запаздыванием по фазе за счет операционного усилителя. Если принять, что Qo и fno - исходные расчетные значения Q и fn, то обычно необходимо корректировать расчетную процедуру, когда Qofno больше, чем 10*.

Рассмотрим теперь, как возникает эффект увеличения добротности в фильтрах, основанных на методе переменных состояния. Найдем сначала фазовый сдвиг для передаточной функции схемы При разомкнутой петле обратной связи с Vbx{s) =0 я Rt и Rs, рав-йыми бесконечности, как показано на рис. 5.5-1. Для этого случая

Увц{5)- l-Л,{s)/{l-адБ) [l+RJRs l + Rb/Re

Если предположить, что Аз{5)СВз/8, то получим

L s + GBJ(l + R,/R,) J

Для установившегося состояния под действием гармонического сигнала это соотношение, если воспользоваться понятием фазоров вч п нч. можно записать в виде

?Я^вч = [Л1+2е+]?Я^п-[Л^-0-]нч. (3)

где, полагая а~{х)по<СВз, получаем

е+=е-= -arctg[Ko№)(i +RjRb)] -(<о„о№)(И-б/б); (4а)

М+ = IСВ,/[] © + СВз/( 1 + RR,)] I : (1 + RjRs);

м- = юв,1[] ©+СБз/(1 + ;?е/5)] I (1+5/ б)-

(46) (4в)

Pkc. 5.5-i. Схема фильтгра, реализованного по методу переменных состояния

Можно представить передаточную функцию от входа Fn и до нч как

нч/п = - 2 СБгД-© + i СБ-1- ©,;©2) - Л1,е„ (5)

где ©2= l/i?2C2, а ©а2, GB2 - соответственно ширина полосы и произведение коэффициента усиления на ширину полосы операционного усилителя Л2. Если GB2>©, то

Л12 ©2/©; е2 = я/2Ч-©2/© Ло-© № (6а), (66)

Следовательно, (3) можно выразить в виде

Можно показать, используя (4), (6) и (96), § 5.2, что если ©~©no. то

Это соотношение показывает, что Qo равно отношению двух величин. Числитель равен произведению коэффициентов передачи через усилитель Лг и инвертирующее звено усилителя Аз, тогда как знаменатель является коэффициентом передачи через неинвер-тирующее звено усилителя A3. Можно записать (7) в виде

= М+ [cos 0+ + j sin 0+-QO cos (9- + 62)- j Qo sin (6 + б^)]. (9)

П

Фазовый сдвиг от Тп ДО Т'вч

sin е+-Qo sin (6-+ 62)

0Д.В = arctg-

(10).

cosG+-Qocos(e--t-e2) Это выражение можно упростить, учитывая, что 6+0 и что

е- + 62 = я/2-[(Й2/сй о Ло-(й„о/СВ2-(<йпо/СВз) (1 + ЗДб) = /2 + е.

(11)

Используя приближенные выражения и тригонометрические со-отношения для cos и sin суммы углов, можно переписать (10) в виде

е+-Qo

= -arctg

iHBarctg-,---

Оо+( о/СВз) (I + Re/Rb)

1-fQt

[сОпоЛо GS2 GB Так как аргумент арктангенса в (12) велик, то

2 по со о

(1+Re/Rb)

(12)

. со о Ао GBz

. (13)

Qo + {o/GB,)(l+R,/R)

Добавляя полученное к фазовому сдвигу, вызванному инвертирующим интегратором [см. (7), § 5.4], получаем общий фазовый сдвиг Вт схемы, основанной на методе переменных состояния, при разомкнутой петле обратной связи

1 + Qo [соя/сопру^о-С) е/СВг-(озе/СВз) (l+Re/Rt)] Qo+(<m/GBs){l + RJR,)

(14)

В идеальном случае Ло и все величины GBf - очень большие, следовательно 6т стремится к значению 1/Qo. Поэтому для небольших отклонений

0г

(ОпьАе GBi

поЛ GBi 1 -f Qo К/ЮпоЛ- no/GB2-( пв/Обз) (1 + Re/Rt)] Qo+(o>nom(l+Re/Rb)

(15)

в результате получаем фактическую величину Q, выраженную через Qo и параметры реализации.

Пример 5.5-1. Эффект увеличения добротности фильтра, основанного на методе переменных состояния. Требуется синтезировать фильтр по методу переменных состояния с Яо=1 я Qc)=10, жиотуя при этом операционный усилитель лЛ741. Желательно найти значение (а„, при котором реализация становится неустойчивой. Из табл. 5.3-1 i?6i?6=l/10, coi=l/TOtt)n и С02= =1/10 а„. Приравнивая знаменатель (15) нулю и полагая GBi=GB (i= . = 1, 2, 3), получаем

(VlOMo-(Bn/GB) (Qo+ 1.1 a /GB) + 1 + Qo(-l/l0Mo-2,1 ш„/СВ) = 0. (16)

JaK как член Ю/Лр пренебрежимо мал, то (16) приводится к виду

(СВ/со )2-31 (GB/co ) -1,1 =0. (17)

Решая эхо уравнение относительно GB/con, получаем приблизительно 31. Следовательно, максимально возможная частота fn для GB= 1000 кГц равна 32,26 кГц. Заметим, что это соответствует нормированному значению GB, т. е. GBn. равному 31. ♦

Можно применить результаты анализа, проведенного выше, к задаче компенсации результирующего увеличения добротности. Из (15) следует

Q l/(l/Qo-3,ltujGB), (18)

где предполагается, что GB\ = GB2=GBzGB, Оо>а>п1СВ, Re/Rs - =0,1 и что член с Ао не оказывает влияния на реализацию. Выражение (18) можно переписать в виде

/ Q l/(l Qo-3,l/GB), (19)

где GB теперь выражено в герцах. Аналогичный результат для резонаторного фильтра будет получен в § 5.7; он имеет вид

/ Q !/(! Qo-4/GB), (20)

где GB также выражено в герцах. Выражения (19) и (20) полезны при проектировании схем, основанных на методе переменных состояния, и резонаторных схем, когда произведение fnQo становится большим. График зависимости этого произведения от fnQ показан на рис. 5.5-2 для двух реализаций: резонаторной и основанной на методе переменных состояния. Предполагается, что произведение коэффициента усиления на ширину полосы равно 1 МГц. Эти кривые могут использоваться для вычисления пре-дыскаженного значения Q, используемого при расчете. Чтобы осуществить это, начнем с величины fnQo и отложим ее значение по горизонтальной оси, показанной как ось fnQ- Проецируя это значение вверх до пересечения с соответствующей кривой (резонаторной реализации или реализации по методу переменных состояния), получаем точку, которая проецируется затем на вертикальную ось, показанную как ось fnQo, и считываем предыскаженное значение величины fnQo- Значение Qo, полученное путем деления этого про-

изведения на fn, и будет тем числом, которое следует использовать в процедуре синтеза. Если fn величина постоянная (что может быть только приблизительно верным), то фактическое значение Q будет близко к желаемому Qo-

J i, 5 6 783

Рис. 5.5-2. Кривые, иллюстрирующие эффект увеличения добротности:

/ - е резонаторных фильтрах и 2 - в фильтрах, реализованных по методу переменных

состояния

Пример 5.5-2. Синтез фильтров (резонаторного и основанного на методе переменных состояния) с использованием предыскаженного значения Qo. Требуется найти дредьюкажеиное значение Qo, которое должно быть использовано для синтеза резоиаторной реализации н реализации по методу переменных состояния с Q=10 и / = 10 кГц. Предполагается, что произведение коэффициента усиления на ширину полосы равно 1 МГц. Для обеих реализаций исходное значение произведения fnQo равно 100 ООО. Для схемы, осно-Bamioft на методе переменных состояния, рис. 5.5-2 дает предыскаженное значение fnQo, равное 75 760. Поэтому предыскаженное значение Qo равно 7,57. Для резоиаторной схемы предыскаженное значение fnQo равно 71430. Следовательно, предыскаженное значение Qo равно 7,14. Заметим, что для резоиаторной схемы требуется большее предыскажение, ф

Одной из проблем при синтезе высокодобротных схем является измерение полученного Q. Обычные методы требуют измерения ширины полосы на уровне -3 дБ. Однако при высокой добротности ее трудно определить, так как она очень мала. Другой подход для измерения добротности состоит в подаче на вход системы ступенчатого воздействия и анализа полученной во временной области реакции. Чтобы показать, как это делается, рассмотрим обобщенную передаточную функцию вида

2 {s)/\\ is) = N (s)/[s -Ь (o /Q) s -f = N (s)/[(s + a) -f p], (21)

где N{s) - полином числителя и

a = o)J2Q; р = (й„1/1-1/4 0Г (22)