схема хорошо известна как универсальный активный фильтр, изготавливаемый в виде микросхем отдельными производи-елями.

Схема модифицированного фильтра, основанного на методе переменных состояния, приведена на рис. 5.3-1. Она отличается от исходной схемы на рис. 5.2 - 2 двумя резисторами Ri и R&, кото-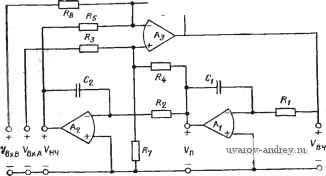

Рис. 5.3-/. Моянфицированная (универсальная) схема активного фильтра, ос- наваяного на методе переменных состояния

рые добавлены для того, чтобы сформировать новый вход Vbxb-Вход исходной схемы обозначен как Vex л. Анализ схемы на рис. 5.3-1 начнем с того, что положим Квхв = 0 и выразим Квч (s) как функцию всех входных напряжений усилителя Аз. В результате получим

R3\\R7

V RdRj

где символ II указывает на параллельное соединение связанных им элементов. Чтобы упростить выражение, обозначим

?4ll?7 RiR? . . 1

Rs + RM7 Rs R7 + RsRi + RiR7 1 -Ь Rs/Ri + Rb/R R3]\R7 RaR7 1

(2a) (26)

Ri + RM7 R3R4. + RaR + RiR7 1 + RJRa + RJR7

KsRe/Rb, K, = RjRs. (2b), (2r) Используя введенные величины, можно переписать (1) в виде ч is) = Iki V л is) + К, Кп Ш {l+Ks + Ki)~K, 1/нч (s)- (3)

Модель 881 фирмы Бекман , модель FS-50 (FS-51) фирмы Болдуин Электронике , модель цАК-2000 фир1мы Интегрейтид Майкросистем , модель AF-100 фирмы Нейшнл Семикондактор , модель UAF-41 фирмы Барр Браун Рисерч.корп. и модель ACF-7092C фирмы Дженерал Инструмент корп. .

Теперь определим

a)i=l ?iCi и (02=1/22 (4)

и заметим, что

. ; Гп(5)=-(ш1/8)Квч(5); (5)

VH4is)=~MVu{s) = {(o,aJs)V{s), (6)

тогда (3) можно переписать в виде

B4(s) = -(1 +Ks + Ki)M,/s)Vn(s)-

-{KsO(oJ)Vnis) + {l+Ks-{-Ki)KryA{s). (7)

Решая это уравнение, получаем передаточную функцию верхних частот для схемы на рис. 5.3-1 при условии, что Увхв = 0:

Если Fbxb = 0, то можно положить Rs = (x>, так что Ki=0. В этом случае (8) может быть записано в виде

Полосовую передаточную функцию и передаточную функцию нижних частот для схемы на рис. 5.3- 1 при условии, что Квхв = = 0 и i?8 = oo, можно найти, используя выражения (5) и (6). В результате

нч() {l+Ks)Kl<i>lC!>2 JJ4

Приравнивая знаменатели (9) и (10) или (И) стандартному полиному второго порядка, получаем уравнения вида

Сравнивая (9), (10) и (11) соответственно с общим видом передаточных функций нижних частот, полосовой и верхних частот второго порядка, получаем выражения для Яо, приведенные ниже:

для ФНЧ [см. (1), §4.2]

Яо = (1-[-/Сз)/С1 Сз = (1 +адб)/(1+ад4 4-ад); (13а) для ПФ [см. (1), § 4.3]

Ho=-KjK=~RJRs; (136)

для ФВЧ [см. (16) , § 4.3]

Ho{i+Ks)K,={i+Re/RMi+Rs/Ri-{-Rs/R,)- (13в)

Типичными в данном случае являются значения: К=0, 1, Ci - = 2=1000 пФ, i?4=-/?5=100 кОм и /?б=10 кОм. Для этих значений (12) и (13) можно привести к следующим выражениям:

to = ]/ю1 ю,/10 = 3,162 тУКЩ (14а)

Q=28.748(1/100 кОм+Щд+1/Я,)У^Ж; (146)

для ФНЧ

Яо=11/[1-1-?з(1/100 кОм4-1/ед (14в)

для ПФ для ФВЧ

Яо=-100 кОм ?з; (14г)

Яо=1,1/[1 + /?з(1/100 кОм-f 1 ?,)]. (14д)

Процедуру синтеза, использующую указанные выше значения, а именно: Ci = C2=1000 пФ, Ri=Rs=lOO кОм, Re=lO кОм, R8=oo и, кроме того, R1-R2, для схемы из рис. 5.3- 1 с Квхв = 0 можно представить в следующем виде. Из (14а) имеем

Ri = R5,0329 10* кОм. (15)

Значения Rs и Rj находим из (146), используя (14д). Полагая [Яо] = 1, получаем

для ФНЧ

для ПФ для ФВЧ

/?з = 316,2 kOm/Q; (16а)

/?з=100кОм; (166)

/?з = 31,62 kOm/Q. (16в)

Решая (146), находим

i?7=100 kOm/(3,4785Q-1 - 100 кОм ?з). (17)

Подставляя (16) в (17), получаем: для ФНЧ

/?,= 100 kOm/(3,162Q-1); (18а)

для ПФ

i?,= 100 kOm/(3,4785Q-2); (186)

для ФВЧ

100 кОм/(0,3162(2-1). (18в)

Заметим, что для ФВЧ добротность должна быть больше, чем У~Т0. Если такой нижний предел Q неприемлем, то отношение R2IR} можно подобрать так, чтобы понизить этот предел. Если произведение Ri и R2 равно исходному значению произведения, когда Ri и R2 были равны, то в этом случае изменение отношения 2/1 будет модифицировать только добротность. Этим заканчивается процедура проектирования функций. цепи, у которых Яо равен единице.

Пример 5.3-1. Инвертирующий ПФ, основанный на методе переменных состояния, с единичным усилением. Требуется синтезировать ПФ с Q=29, =1 кГц и Яо=1. В соответствии с процедурой синтеза, ириведенной выше (/?8=оо, Увхь=0), имеем Ri=Ri=lOO кОм, Лб=10 кОм и Ci = C2=11000 пФ. Из (15) получаем i?i=i;?2= 50,329 кОм, из (166) -/?з=100 кОм и из (186) - ./?7= 1,480 кОм. (См. пример 5.2-1 для реализации, осиованиой на методе переменных состояния, в которой \Но\ф1.) ♦

Интересно исследовать относительные значения модулей Унч{]()у (3<й) и (j( >) для фильтра на рис. 5.3-1. Если положить, что Сй1=(й2 и кб/к5=0, 1, то из (12а) следует, что ©i = =ft)2= l/10ft)n=3,162 © . Равенство (6) показывает, что для некоторой постоянной частоты (Ох справедливо соотношение

IVh4(J J 1=3,162

©71

ln(J Jl = 10

\Увч{М- (19)

Таким образом, уровень сигнала на различных выходах схемы может отличаться в 10 раз. Заметим, что это может вызвать насыщение, даже если вычисление амплитуды выходных напряжений на некоторых выходах не указывает на это.

Чтобы закончить общее знакомство с модифицированной реализацией, основанной на методе переменных состояния, необходимо рассмотреть использование входа, обозначенного Vbxb. В указанной схеме имеем Vbxa=0 и Rs=oo (см. рис. 5.3-1). Следуя процедуре, аналогичной той, что была применена для данной схемы в случае, если входом служила точка, обозначенная Vbka, можно найти ,

(20)

Это выражение можно упростить:

1вч (s) = -(1+ 3 + к,) щ Fb4 (s)/s-

-(а),со,адвч(5)-/<:41вхв(8), (21)

если воспользоваться (2), (6) и учесть, что К2=1{+R4Ri), так как Rs = cx>. Решив это уравнение относительно передаточной фунщии верхних частот, получим

Vn4{s)/VBxB{s)=~KiS/[s + {l+Ks+Ki)K(iS+fKs]. (22)

(6) можно использовать д верхних частот и полосовой.

нч(*) -coicogK * 24)

Уравнение (6) можно использовать для получения передатоЧ' ных функций верхних частот и полосовой. В результате

Сравнивая (9), (10) и (11) с полученными выше тремя выражениями, видим, что универсальный активный фильтр дает возможность реализовать ФНЧ, ПФ и ФВЧ второго порядка с фазовым сдвигом О или 180° на частоте, для которой определяется Яо. Приравнивая (22), (23) и (24) стандартной функции второго порядка соответствующего типа, получаем следующие соотношения:

а) = VcoTTa = V{RM/RiR2CiC; (25а)

i = (l+/3 + /.)/.l/= l/m- (256)

Значения Яо для этих трех случаев следующие: для ФНЧ

Яо = -KjKs = - RjRs. (26а)

для ПФ

Яо=---=-i + RjR,- (266)

K2{i + Ks + Ki) i + Rs/Re + Rs/Rb

для ФВЧ

Яо=-/С,= -ад. (26в)

Полагая, что /?4=/?s = 100 кОм, /?б=10 кОм и Ci = C2=1000 пФ,

как это делали и для схемы со входом, обозначенным Vbxa{s), получаем

а) = 3,162.10 /1/7Г; (27а)

Q = 0,3162 VRM + ; (276)

для ФНЧ

Яо=-100 kOm/R; (27в)

для ПФ

1 + 100 кОм ?, 1 -I- 100 kOm/R, . ,2jj,4

l--i?8/10 кОм--;?з/100 кОм 1--/?8/9,091 кОм

ДЛЯ ФВЧ

я =1оад. (27д)

Процедуру синтеза для входа Vbxb можно получить, если воспользоваться данными значениями и, кроме того, принять Ri = =R2- Значения Ri и R2 находим тогда из формулы

Ri = R5,0329 1 OV/n кОм. (28)

Полагая Яо1 = 1 в (27), получаем следующие формулы для расчета сопротивления Rs: для ФНЧ

i?8=100 кОм; (29а)

для ПФ

/?8 = 31.62Q кОм; (29б>

для ФВЧ

10 кОм. (29в)

Решая (276) относительно и учитывая, что Ri=R2, находим

R, = m kom/[3,162Q(l,l + 10K/i?8)-1].

Подстановка (29) в (30) дает: для ФНЧ

для ПФ

для ФВЧ

7?, = 100 кОм/(3,7947 Q- 1);

7?-=100 kOm/3,4785Q;

(30>

(31а> (31б> (31в>

R, = 100 кОм/(6,6402 Q- 1).

Пример 5.3-2. Неинвертирующий полосовой фильтр, основанный на методе переменных состояния, с единичным усилением. Пусть требуется спроектировать неинвертирующий ПФ с Q=20 и /п=1 кГц, используя вход Vbi в-на рис. 5.3-1. В соответствии с процедурой синтеза имеем: ./?4=i/?6=100 кОм,. J?6=10 кОм и Ci=C2=1000 пФ. Поэтому из (15) находим, что /?,=J?2= =50,329 кОм. Из соотношений (296) и (316) следует i/?8=632,40 кОм и J?7= = 1,437 кОм, Из (27г) определяем: Яо=1. ф

В табл. 5.3 - 1 сведены основные результаты процедур синтеза для модифицированного активного фильтра, основанного на методе переменных состояния, различных конфигураций (нижних час-

Таблица 5.3-1

Расчетные соотношения (в иизкочастотной области) для активного фильтра, реализованного по методу переменных состояния, Яо=1*

Параметр

Неиивертирующая реализация

ФНЧ

ФВЧ

Инвертирующая реализация ( 3 = ; VBxA=f>)

ФНЧ

ФВЧ

Фазовый сдвиг передаточной функции на частоте, где определяется Яо

Hi, Ла, кОм

Лз кОм Лв, кОм

Лу, кОм

0°

5,0329-10

316,2/(2

3,162 (2-1

± 180° 5,0329-10*

5,0329.10*

fn 100

31,62/(2 100

3,4785 (2-2

0.3162 (2-1

±180° 5,0329-10*

0°

5,0329-10*

100 100

31,62(2 100

3,4785 (2-1

3,4785 Q

±180° 5,0329-10*

100 6,6402 Q-t

* Процедура синтеза предполагает, что Л1=Л2, Л4=Лз=100 кОм, Лб=10 кОм, C,=Cj= = 1000 пФ.

тот, полосовой и верхних частот) при использовании как входа вхА, так и Увхв. Расчетные соотношения этой таблицы справедливы до тех пор, пока / много больше, чем GB операционных усилителей. Широкие возможности такой универсальной реализации активного фильтра хорошо показаны в таблице.

Рассмотрим теперь вопрос настройки универсального активного фильтра общего применения. Типичная схема фильтра с внешними резисторами Ru R2, Rb, Ri и R& показана на рис. 5.3 - 2. Ре-.зисторы Ri Vi R2 используются для настройки п- Для неинверти-рующей схемы или (в случае ПФ) могут использоваться для шастройки Q; Rj и R [исключая случай ПФ) можно также использовать для настройки Яо. Для инвертирующей схемы и Rs, можно использовать для настройки Q хотя Rs и Ri (только в слу- чае ПФ) могут использоваться и для настройки Яо.

1 1 ! ! JL

вх..г

И I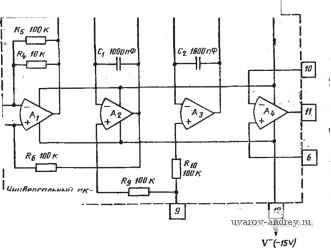

\тивмыи фильтр

IPuc. 5:3-2. Типичная практическая схема универсального активного фильтра. Из, Л? и Rb определяют добротность и коэффициент усиления; Ai, А2, Аз к Ai - операционные усилители типа р,Л741; Ri и R2 используются для установки требуемой собственной частоты

Теперь можно подвести некоторые итоги исследования универсального активного фильтра. Прежде всего рассмотрим уровни сигналов в усилителе. Это важно, так как высокие уровни сигналов требуют и высокой скорости нарастания сигнала на выходе усилителя (см. § 5.4), а слишком высокая скорость нарастания может вызвать его неустойчивость. Обычно размах максимального выходного напряжения универсального активного фильтра общего назначения составляет 20, 8 и 2 В для выходов ФНЧ, ПФ и ФВЧ соответственно. Эти предельные значения вьщерживаются в диа-

пазоне частот от 10 Гц до 1 кГц. На частоте 10 кГц размах вьа-ходного напряжения уменьшается до 8, 3 и 0,8 В соответственно.. Эти значения получены при напряжении питания ± 15 В. Рассмотрим теперь максимально достижимую добротность универсального активного фильтра. Она составляет примерно 50 и определяется прежде всего, частотной характеристикой операционного усилителя и потерями в конденсаторах. При конструировании универсальных активных фильтров, реализующих большие добротности разумнее всего использовать процедуру, приведенную для Яо = 1 в табл. 5.3- 1. Если требуется большее значение коэффициента усиления, то можно использовать дополнительный, не входящий в стандартную схему универсального фильтра усилитель.

Универсальный фильтр общего назначения используется обычно до частот порядка 10 кГц. Выше этой частоты важное значение приобретает эффект увеличения добротности, описанный в § 5.5,. что делает настройку более сложной. Хотя запаздывающий фазовый сдвиг благодаря конечному значению GB может быть скомпенсирован введением опережающего фазового сдвига (путем шунтирования Ri и/или R2 малыми емкостями), остаются проблемы, связанные с ограничениями, налагаемыми на зфовень сигналов и допустимую скорость нарастания. Для частот выше 10 кГц, должны использоваться высококачественные универсальные фильтры. Так, используя гибридные схемы, можно расширить диапазон до 100 кГц и более. Использование в этом случае высококачественных усилителей, естественно, приводит к удорожанию стандартных универсальных активных фильтров.

5.4. Интеграторы

Было показано, что использование операционного усилителя в; качестве интегратора имеет существенное значение в реализациях активных фильтров, представленных в § 5.2 и 5.3. Здесь рассмотрим некоторые детали, связанные с таким использованием, и прежде всего инвертирующий интегратор. Его основная схема приведена на рис. 5.4--1. Для нее

А(S) = l/ (s)/l/,is) = l-Aais)(ORcl{s + (ORc)]in +Aa{s)s/is + (i>j,c)], (1>

где u)Rc= I IRC. (2>

Используя модель с доминирующим полюсом для Ad{s) [см. (17) в приложении В], получаем

A{s) = Vo{s)/VAs)=--(ORcGB/ls + {(Oa + (iiRC+GB)s+(ownc]. (3>

Если (йа<; )дс ДЛЯ значений о, меньших, чем GB, то амплитуду (3) можно аппроксимировать следующим выражением:

IЛ (j со) I (Оде GB/(oV(+GB (4>

Фазу (3) можно записать как

argH(ju))] = n-arctg[u)(u) -l-u)/jc + G5)/(u) ft)/jc-и*)]. (5>

Если (Оа и (Оке меньше, чем GB, то (5) можно привести к виду

arg [А (j О))] лгя-arctg [ю С5/((о„ (Одс-со)]. (6)

В этой связи надо отметить, что аргумент функции арктангенс много больше единицы. Следовательно, (6) можно аппроксимировать выражением вида

argH(ju))]л/2-f й)оСйдс/£йСБ-©/GB = n/2-f ©;;с/й)Ло-w/GB. (7)

Это выражение позволяет выявить ряд важных особенностей ар актеристик инвертирующего интегратора. В частности, видно,

что уменьшение Л о приводит к опережению по фазе, тогда как увеличение отношения a/GB вызывает запаздывание по фазе. К сожалению, второй член в (7) $ много меньше третьего, поэтому взаим-Ч, ная компенсация фазовых сдвигов не-.5 возможна. Если начертить диаграмму Боде для Л (jco), определяемую (3), как показано на рис. 5.4-2, то увидим, что существуют две различные области полученных частотных характеристик. Первая из них соответствует частотам (о<(олс- Для нее

А (s) = Vo is)/V, (s) -(О, Ло/(з + ©J. . (8)

Вторая область, частот определяется соотношением.

GB. В этой частотной области выражения (4) .и (7) могут использоваться для анализа частотных характеристик инвертирующего интегратора.

Рис. 5.4-/. Схема иввер-тирующег-о интегратора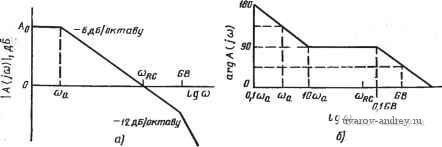

Рис. 5.4-2. Диаграмма Боде для инвертирующего интегратора (рис. 5.4-1): а - логарифмические АЧХ; б - ФЧХ

Входное полное сопротивление инвертирующего интегратора в основном определяется сопротивлением входного резистора R. Оно практически не влияет на характеристики активного фильтра. Выходное сопротивление операционного усилителя, напротив, может оказать значительное влияние на характеристику инвертирующего интегратора. Причина этого заключается в том, что с ростом частоты растет и модуль выходного полного сопротивления инте-

гратора, замкнутого обратной связью. Это говорит о том, что выходное по.пное сопротивление интегратора имеет явно выраженный индуктивный характер, что в сочетании с емкостной нагрузкой создаваемой последующим каскадом, может привести к созданию, комплексных полюсов. Кроме того, могут сформироваться дополнительные нули передачи, что может привести к значительным изменениям высокочастотной характеристики рассматриваемой схемы. Моделировать такой эффект можно, включив резистор Ro последовательно с выходом усилителя, а емкость Сь параллельно-указанному выходу. Полученная эквивалентная схема приведена на рис. 5.4 - 3,с. Схема, пригодная для вычисления Vo{s)/Vsis)

f

Рис. 5.4-3. Влияние вых-одного сооротивлвния операционного усилителя на характеристики Инвертирующего интегратора

показана на рис. 5.4-3,6. Если юнс<С5 и О, то можно показать, что

{s-GBlRoC)IRC

Л(5):

Vo(s)

Vs (s) s\s + s (l/i?o C) + GB {l/Ro )] Полюсы этой функции

PiO (доминирующий полюс интегратора);

Нули определяются так:

-AGBlao); ao=l/RCL.

1,2

±yGB/R,C.

(9>

(10> (П>

(12)

Полюсы р2 и рз становятся комплексными, если (uo<4GB. Для операционного усилителя с номинальным полным выходным сопротивлением при разомкнутой петле обратной связи, равным 50 Ом, и СБ = 1 МГц комплексные полюсы появляются при Cl больше 800 пФ. Два нуля, определенные в (12), устраняют влияние фазового сдвига, так как они являются приблизительно зеркально отображенными относительно оси ]ю. Однако АЧХ благодаря наличию этих двух нулей приобретает наклон 12 дБ/октаву., Эти изменения показаны на рис. 5.4-4, где представлена АЧХ инвертирующего интегратора с (ua<4G5. В качестве операционного' используется усилитель типа яА741 с GB, приблизительно равным 1 МГц. На рисунке показано влияние различных R п С. Зна-