добротных комплексных корней. Если желательно реализовать вьь сокодобротные комплексные корни, то предпочтительнее использовать пятую цепь, которая является двойным Т-образным мостом. Числитель I передаточной полной проводимости двойной Т-образной цепи является полиномом третьего порядка, а знаменатель - полиномом второго порядка. В процессе синтеза в этом случае предполагается, что один из вещественных полюсов (ci или 02) знаменателя будет приблизительно сокращен с корнем чисчителя при -1. Следовательно, остающийся полюс может быть сокращен с членом вида {s+a) в знаменателе передаточной полной проводимости другой цепи. Это предположение оправдывает себя, если добротность комплексных полюсов, которые должны быть реализованы числителем двойной Т-образной цепи, высока.

Пример 5.1-4. Фильтр нижних частот с однопетлевой обратной связью на одном усилителе с бесконечным коэффициентом усиления. Пусть требуется реализовать нормированную передаточную функцию

V2 (s)/Vi (s) = - \0/(s + y2s+ 1). (25)

Так как она соответствует ФНЧ, то из табл. 5.1-1 выбираем цепь типа 2 для цепи А и типа 4 для цепи В. Постоянная а должна быть (равна [/2. Таким образом, из табл. 5.1-1 для цепи В получаем: J?i=0,921 Ом, J?2=0,493Om. Ci=l Ф и С2=2,202 Ф. Если положить для схемы типа 2, взятой в качестве цепи А, что R=Ri=R2, то получим R=a/{2\Ho\). Если С=1 Ф, то R = =0,07071 Ом. Полученная схема приведена на рис. 5.1-7.

Рис. 5.1-7. Схема ФНЧ с однопетлевой обратной связью па усилителе с бесконечным коэффициентом усиления (к примеру 5.1-4). Значения элементов схемы даны в омах, фарадах

Реализация с однопетлевой обратной связью на усилителе с бесконечным усилением, описанная выше, имеет ряд недостатков, которые вызваны, главным образом тем, что цепи А и В должны каждая в отдельности реализовать те же самые собственные частоты. Вследствие этих требований необходимо иметь больше пассивных элементов, чем это требуется для других типов активных фильтров. Например, реализация ФНЧ в примере 5.1 -4 требует трех конденсаторов и трех резисторов по сравнению с двумя конденсаторами и двумя или тремя резисторами в других эквивалентных фильтрах. Кроме того, пассивные элементы должны иметь высокое качество и жесткие допуски, чтобы сокращение подобных членов в числителе и знаменателе было достаточно эффективным. Настройка такой структуры, учитывая требования сокращения подобных членов, достаточно сложна. Если не считать этих недостат-

KGB, МОЖНО сказать, что данная схема дает возможность удовлетворительно реализовать высокодобротные схемы и достичь больших значений Яо без большого разброса номиналов элементов. Кроме того, реализации с однопетлевой обратной связью и бесконечным коэффициентом усиления позволяют реализовать обобщенные функции цепи второго порядка, т. е. такие функции, которые имеют как комплексные нули так и комплексные полюсы и соответствуют общей структуре схемы, обсужденной в § 4.4.

5.2. Фильтр с использованием нескольких усилителей

Вследствие того, что технология изготовления активных приборов получила значительное развитие, многие традиционные установки оказываются недействительными. Одной из таких установок было использование как можно меньшего числа активных приборов. Это привело к появлению фильтров на одном усилителе, которые были рассмотрены в предыдущих параграфах. Однако с точки зрения современной технологии интегральных схем часто оказывается, что нет смысла минимизировать число активных элементов. Поэтому, если реализации на нескольких усилителях могут обеспечить лучшие характеристики, то они могут оказаться предпочтительными по сравнению с реализациями на одном усилителе. Цель этого параграфа - познакомить с двумя видами реализаций на нескольких усилителях. Они называются резонаторны-ми реализациями и реализациями по методу переменных состояния. В них используются от двух до четырех операционных усилителей в зависимости от желаемых характеристик фильтра.

Реализации фильтров по методу переменных состояния (они также называют KHN-фильтрами по начальным буквам фамилий авторов, которые ввели их в практику исключительно

гибки, имеют хорошие характеристики и низкую чувствительность. Эти реализации широко используются разработчиками фильтров широкого применения. Название переменные состояния происходит от переменных, рассматриваемых в теории пространства состояний, методы которой используются для решения дифференциальных уравнений, применяемых в процессе синтеза реализации. Чтобы пояснить это, рассмотрим инвертирующую полосовую передаточную функцию второго порядка

У2 т\ (S) - -1Я| S/(S2 -t- S + Go). (1)

в отечественных ссылках упоминается как метод прост.рапства состояний.-Ярнж. пер.

См. работу [50], а также более раннюю публикацию [51].

Используемый ниже метод так или иначе сводится к методу аналогового моделирования (методу последовательного интегрирования) дифференциального уравнения второго порядка, который был введен в практику значительно раньше цитируемой работы автора [50] и даже раньше [51], см., например, {3*, 4*, 9]. Прим. пер.

Введем в этом уравнении произвольную (в частотной области) переменную X(s) и умножим как числитель, так и знаменатель на X(s)/s, чтобы получить выражение вида

V2{s) -\H\X(s)/s ,2)

Vi{s) X(s) + ciiX(s)/s + aoX(s)/s

Если приравнять отдельно числители и знаменатели левых и правых частей в выражении (2), то получим следующие уравнения:

X (S) = \\ (s)-ai X (s)/s- Оо X {s)/s; (За)

Fa(s) = -X(s)/s. (36)

Если теперь провести обратное преобразование Лапласа обеих частей этого выражения, то получим интегральные уравнения (во временной области)

x{t) = Vi{f)~aix{t)dt-ao[x{t)dt]dt; (4а)

V2{t)==-\H\xit)di, (46)

где x{t)=:L-[X{s)]. Величины x{t), x{t)dt, x{t)dt]dt называются переменными состояния [52], которые и определяют название соответствующего фильтра. Схема для решения системы (4) с помощью аналоговой ЭВМ показана на рис. 5.2-1. Она легко преобразуется в схему фильтра, если использовать операционные усилители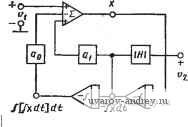

Рис. 5.2-/. Общая структурная схема фильтра, полученная на основе метода переменных состояния

О--о

Рис. 5.2-2. Схема фильтра, построенного на основе метода переменных состояния

для моделирования инвертирующих интеграторов. Полученная в результате схема приведена на рис. 5.2-2. Ее полосовую передаточную функцию можно получить, если учесть, что

Унч()--Vuis)/sRC,; Fn(s)=-Ws)/s/?iCi, (5)

где VH4(s), Vn (*) и 1вч(*) -соответственно выходные напряжения ФНЧ ПФ и ФВЧ. Дополнительно к этому Vtj (s) можно выразить как

B4(S) =

-у

H4(S) +

3 5 + ?в

Rs + R* Rb

Rs + Ri Rb

Используя (5) для того, чтобы исключить Vimis) и Квч

получаем

i+RelRe у , ) l+Re/Rb у ,-Л .74

sRiCi L Rs sRaCi

Решая относительно Vji{s)/Vi{s) приведенное равенство и используя (5), получаем передаточные функции соответственно полосовую, нижних частот и верхних частот

I + Rb/Rb s

l+RaIRi RiCi l+RelRs 1

где D(s) = s-

Ll + Rs/Ri Ri R2 Ci Ca s 1 + RelRb , Re/Rb

/d(s); JDis);

1 1 1 b RilRa i RiRs C1C2

(8a) (86) (8b) (8r)

Заметим, что реализации ФНЧ и ФВЧ являются неинвертирую-щими, тогда как реализация ПФ - инвертирующая. Выражения Мл и Q в этом случае принимают вид

4/3 6 1

Q ~ y + R.

Величина Яо различна для всех трех реализаций: для ФНЧ [см. (1), § 4.2]

1 + RblR l+RsIRi

для ПФ [см. (1), § 4.3]

fig = -RJRaj для ФВЧ^см. (16), §4.3]

1-f ?б/?5

1 + Rs/Ri

(9а), (96)

(10а) (106) (10в)

Если выбрать Rs=R6, Ri=R2=Rs и Ci = C2=C, то (9) примет вид

со = 1/RC; 1/Q = 2/(1 + RjR). (1 la), (11б>

Для выбранных соотношений, используя (И), можно описать следующую процедуру синтеза. L Полагаем, что соп и Q заданы.

2. Выбираем удобные значения для Ci = C2=C и /?з=-5=б.

3. Вычисляем

Ri = R= 1/ш„С; R = (2Q-1)R. (12а), (12б>

4. Яо принимает следующий вид: для ФНЧ и ФВЧ

Ho{2Q-l)/Q; . (13а>

для ПФ

Яо=1-2д. (136)

пример 6.2-1. Полосовой фильтр, реализованный по методу переменных состояний. Пусть требуется синтезировать ПФ на основе (переменных состояний с Q=20 и = 1.кГц. Выберем Ci=Cs=0,01 мкФ и i?3=J?5=i?6= = 10 кОм. Таким образом, из (12) получаем J?i=J?2=15,9 кОм и i?4=390 кОм. Из (10) и (13) получаем Яо=-39,0. Эта же реализация позволяет получить НЧ и ВЧ передаточные функции с Q=20 и f = l кГц при условии исполь-зоваиия в качестве выходных соответствующих зажимов схемы на ,рнс. 5.2-2. Яо для этих реализаций равна 1,95. ф

Одна из причин популярности фильтров на основе переменных состояния - низкие чувствительности основных характеристик. Используя определения § 3.5 и соотношения (9), находим

SL с. -si с. = -Sn = Sn 1/2; (14а) Si - -1/(1 + RM = -Sj (146)

Анализ этих соотношений показывает, что чувствительность добротности к Rb и Re можно свести к нулю, если выбрать /?5= -Re. Модули всех оставшихся чувствительностей меньше единицы причем большинство из них равно 1/2. Чувствительности добротности к коэффициенту усиления операционного усилителя для данной реализации даже меньше этой величины и имеют порядок QIKo, где Ко - коэффициент усиления операционного усилителя при разомкнутой петле обратной связи [47]. Вследствие такой низкой чувствительности фильтр на основе переменных состояния успешно использовался для реализации передаточных функций с добротностью до нескольких сотен. Методы построения таких фильтров можно распространить на случай п-го порядка [13].

Второй тип фильтра на нескольких усилителях, который обсуждается в этом параграфе, - резонаторный активный фильтр [53].

Основной подход в данном случае состоит в использовании ДС-генератора с отрицательной обратной связью. Этот метод именуется также методом образования биквадратного фильтра. Будем предпочитать название резонаторный фильтр, так как слово биквадратный (или биквад) используется также для описания класса передаточных функций. Резонатор можно получить из общей схемы аналогового моделирования генератора колебаний, как показано на рис. 5.2-3. Без отрицательной обратной связи эта схема дает решение дифференциального уравнения

х (0 + со2х(0 = 0 виде

x{t) = Asin4if,t.

Отриаатель-ная аоратная связь

(15)

Рш. 5.2-3. Общая структурная схема фильтра, основанная на модели резо-(16) натора (резонаторный фильтр)

Использование вместо интеграторов операционных усилителей на рис. 5.2 - 3 приводит к схеме, показанной на рис. 5.2 - 4, которая и называется резонаторным активным фильтром. Резистор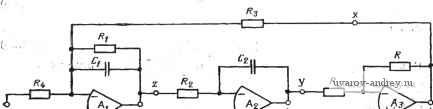

Рис. 5.2-4. Схема резонаторного фильтра

Ri обеспечивает отрицательную обратную связь. Входной сигнал Vt подается на схему через сопротивление Ri. Анализ этого фильтра начнем с нахождения Vyi{s)/Vi{s), лричем (s) можно выразить следующим образом:

VAs) = -VH4is) = Vis)/sR,C (18)

так что, подставляя (18) в (17), получаем полосовую передаточную функцию резонаторного активного фильтра

Vu{s)/Vi{s){-s/R,CMs + s/RiC+VR2RsCiC)- (19)

Эта передаточная функция привлекательна своей простотой. Теперь можно легко получить передаточную функцию нижних частот подстановкой (19) в (18). В результате

нч is) - mR, Cl C,)/ls + s/Ri Cl + 3 Cl CJ. (20>

Чтобы получить инвертирующую реализацию ФНЧ, следует взять в качестве выхода ФНЧ выход инвертора, идеальный интегратор между зажимами х и у можно заменить инвертором между зажимами у а z для того, чтобы создать неинвертирующую полосовую передаточную функцию на выходе Vx. Схему на трех усилителях (см. рис. 5.2 - 4) нельзя использовать для формирования передаточной функции верхних частот.

Приравнивая знаменатель выражения (19) и знаменатель стандартной полосовой передаточной функции второго порядка [см. (1), § 4.2], получаем

(Onl/VRRsCCi, 1/Q = (! ?,)У/?a/?3Ca/Ci; (21а), (216)

Из этих соотношений находим, что чувствительности Q и соп очень низкие, а именно, их значение не превышает либо 1, либо 1/2. Выражения для Яо имеют следующий вид:

для ФНЧ:

Яо = /?з/4; (22а)

для ПФ

\Ho\=Ri/R. {226}

В этом случае можно предложить следующую процедуру синтеза.

1. Полагаем, что cuni Q и Но заданы.

2. Выбираем /?2=/?з=/? и Ct = C2=C.

3. Принимаем то или иное значение для R или С и находим значение оставшегося С или R из формулы

со =1 ?С. - (23а)

4. Вычисляем: для ФНЧ для ПФ

RiQR; (236)

R, = R/H ; (23в)

R,Rj\Ho\. (23г)

Пример 5.2-2. Резонаторный активный фильтр. Пусть требуется синтезировать резонаторный активный фильтр второго порядка (ФНЧ и ПФ) с добротностью 20 и f = l кГц (Яо=1). Выбираем Ci=C2=C=0,01 мкФ. Таким образом, J?= 15,915 и J?i =318,31 кОм. Для реализация ФНЧ i?4= = 15,915 кОм и для реализации ПФ /?4=318,31 кОм. ф

В ЭТОМ параграфе были рассмотрены две наиболее удачные реализации активных фильтров второго порядка из тех, которые бу-

дут рассматриваться далее в этой книге. Из этих двух фильтр, реализованный по методу переменных состояния, обладает тем преимуществом, что дает возможность реализовать на его основе не только ФНЧ и ПФ, но и ФВЧ. Схема, основанная на методе переменных состояния (см. рис. 5.2 - 2), пригодна также для реализации (1), § 4.4, при наличии одного дополнительного усилителя. Этот усилитель используется для суммирования выходных сигналов фильтров нижних частот, полосового и верхних частот, чтобы создать биквадратную реализацию. Если хотят реализовать (1) с

±

Рис. 5.2-5. Реализация биквадратной функции цепи по методу переменных состояния

я, bi и Ъо (все они больше нуля), то можно использовать схему, показанную на рис. 5.2 - 5. Так как ФНЧ- и ФВЧ-реализации положительны, то они подаются на неинвертируюший вход А^. Тогда можно написать

1+7/8 10 l-t-Ag/f,

Используя (8) и (24), получаем

s2 + -

Vi{s) l+i?9/?io +RelRb

Vi{s) l+R,/Rs i+Ra/Ri

s 1 + R,/Rs

R7/R8

Rii -{-Rio/Ra RiRzCiCs

s 1 + RjRb

Re/Rb

RiCi 1+RJR3 R1R2C1C2

Один из вариантов упрощения этих уравнений - положить /?э=/?5=?8=/?9=1 и /?iCi=i?2C2= 1 с. Таким образом,

2 (S) j?4 (1 + /?б) (1 + Rio) s+sil+ R,)/(l + Rio) + Viis) Rio + s + s{l+Re)/{i+Ri)+RB

Приравнивая (1), § 4.4 к (26), получаем

(26)

(27a) (276)

P = VRe, Qp = VRe{l+RMl+e)-Из этих выражений видно, что резонаторный фильтр, основанный на методе переменных состояния, можно проектировать так, чтобы использовать Re и Rj для управления сор и coz, а i?4 и Rw для управления Qp и Qz. Кроме того, ули можно сдвинуть в правую половину комплексной плоскости путем подключения , Rio к неинвертирующему входу выходного сумматора Л4. В этом случае необходимо заземлить инвертирующий вход Л4 через дополнительный резистор, а значения элементов R7, Ra и Rio пересчитать (см. задачи в конце главы).

Этот резонаторный фильтр можно также использовать для реализации биквадратной передаточной функции. Для модификации этой схемы сначала повернем ее против часовой стрелки так, чтобы выход операционного усилителя Ai стал крайним слева. Добавляется еще один конденсатор Сз, а входной сигнал подается одно-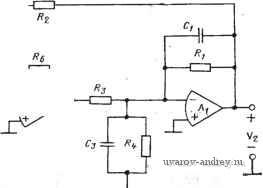

Рис. 5.2-6. Реализация биквадратной функции цепи, основанная на модели

резонатора

временно на входы всех усилителей (рис. 5.2 - 6). Можно показать, что передаточная функция этой схемы

8 3 / 3

F2(S) -Сз

\ Ri

R3 Rb Ri 2

(28)

Vi(s) Cl + s/RiCi+Re/R2RsRbCiC2

Расчетные соотношения для этой реализации приведены в табл. 5.2-1, где указаны значения соответствующих элементов для раз-

Таблица 5.2-t

Соотношения для синтеза и элементы настройки схемы на рис. 5.2-6

Значение Сэ может быть фиксировано, если коэффициент усиления в полосе пропускания является свободным параметром.

ЛИЧНЫХ видов функции второго порядка. Приравнивая (1), § 4.4, и (28), получаем

RgRb RiCa С3 Qj. \ Ri R3 Rs I Re Cg

l/ 6 J 1 i/ RsRsRbCa

P V RiRsRbCiC Qp Ri У RtCi

(29a)

.abiC Qp~ Ri У /?70

Пример 5.2-3. Требуется получить реализацию фильтра второго порядка, используя схему на рис 5.2-6. Исходные данные т-аковы: / =1,6 кГц, /р = = 1,5 кГц, Qi=oo и Qp = 10. Желательно иметь коэффициент усиления для нижних частот, равный -1.

Из табл. 5.2-1 шидно, что J?4=8=oo. Если выбрать J?3=6=iR6=10 кОм и Ci=C2=0,01 1М1кФ, то из (29) имеем: i?i = 106,l кОм и iR2=lll,26 кОм. Коэффициент усиления для нижних частот определяется отношением -(R2Ri)-Следовательно, для того-чтобы удовлетворить исходным требованиям, Ri должно быть равно lil,3 кОм. Так как определены все элементы, кроме Сз, то, воспользовавшись (29а) и зная со, находим, что Сз=8,76-10- Ф. ♦

Следует отметить, что схема на рис. 5.2 - 6 пригодна для реализации ФВЧ.

5.3. Универсальный активный фильтр

Одно из ограничений на фильтр, основанный на методе переменных состояния и описанный в предыдущем параграфе, состоит в том, что полосовую функцию цепи можно реализовать только в инвертированной форме, хотя функции цепи нижних и верхних частот могут быть реализованы как неинвертирующие. Кроме того, для определенной процедуры синтеза значение постоянной Яо нельзя выбрать свободно. В этом параграфе представим реализацию модифицированного фильтра, основанного на методе переменных состояния, которая позволит преодолеть эти трудности. Эта