для полосового фильтра показаны на рис. 1.3-4. Диапазон частот, которые пропускаются фильтром, называется полосой пропур-кания, ширина которой {BW) определяется как разность межДу частотами среза полосы пропускания. Используя Иг и coi, как показано на рисунках, в качестве верхней и нижней частот срра, получаем

BW = (U2-CDi. / (5)

Средняя частота ©о полосы пропускания определяется как/среднее геометрическое частот среза. Таким образом,

cuo = KtV. / (6)

На рис. 1.3-4,а показана идеальная (нереализуемая) характеристика полосового фильтра. На рис. 1.3-4,6 показана таракте-ристика, монотонная в том смысле, что производная АЧХ/ взятая

й), UJ 2 I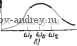

и, 01г

и, Ua (Jj

Рис. 1.3-4. Бия основных АЧХ ПФ

отдельно слева и справа от средней частоты, не меняет знака. Аналогично этому на рис. 1.3 - 4,в и г характеристики в полосе пропускания - равноволновые, а за пределами полосы пропускания- монотонные. И, наконец, на рис. 1.3-4,д показана эллиптическая характеристика полосового фильтра. Ее амплитуда на нулевой и бесконечно большой частотах может быть равна нулю или (как показано) быть ненулевой. Все АЧХ полосовых фильтров, показанные на рис. 1.3 - 4,а-г, составляют функции цепи, у которых в общем случае половина нулей находится в начале координат, а другая половина - в бесконечности. Следовательно, с учетом того, что эти функции рациональные, они имеют вид

N{s) = Hs /yB{s), (7)

где Н - постоянная, а п - степень полинома в знаменателе B(s), величина всегда четная. Фазочастотная характеристика для такой функции начинается со значения ( + 90п/2)° при нулевой частоте и уменьшается до (-90 п/2) в бесконечности. Она равна нулю на средней частоте.

Существует много других типов функций цепи, например, таких, которые имеют режекторные или всепропускающие характеристики. Л1ы рассмотрим их позднее.

1.4. Нормирование частоты и полного сопротивления

Технические требования, которые обычно задаются при проектировании фильтра, указывают реальные значения частот, которые могут составлять тысячи герц. Ясно, однако, что расчет фильтра

Мачительно облегчается, если использовать частоты в несколько Х)Ц или радиан в секунду, так как вычисления при этом упроща-[оТся (а вероятность ошибки уменьшается) - нет необходимости использовать различные степени десяти. В расчетных таблицах для различных характеристик фильтров также используются такие удобные значения частот. Их обычно называют нормированными значениями частоты. Для преобразования нормированных значений \ реально существующие частоты, требуемые для того или, иного конкретного применения, используется процедура денорми-рования частоты} Она включает в себя замену переменной комплексной частоты. Если рассматривать р как нормированную переменную комплексной частоты, а s как денормированную, то процедура! денормирования частоты будет определяться соотношением

\ s-finP. (I)

где fin V~ постоянная денормирования по частоте. Например, рас-CMOTpHjA катушку с нормированным по частоте значением индуктивности L генри и нормированным по частоте полным сопротивлением Znip) =pL. Денормированное полное сопротй^вление Z(s) находится из (1) и равно sL/fi , следовательно, оно соответствует индуктивности L/Qn. Аналогично, денормированная емкость будет иметь значение C/Qn- Основываясь на этом, легко получить дополнительные соотношения для других элементов цепи, подвергнутых денормированию по частоте. Сводные результаты такого денормирования приведены в первой строке табл. 1.4-1.

Таблица 1.4-1

Влияние денормирования по частоте и полному сопротивлению на элементы цепи

Примечание. ИНУН - источник напряжения, управляемый напряжением, ИТУТ - источ- тока, управляемый током, ИТУН - источник тока, управляемый напряжением, ИНУТ - сочник напряжения, управляемый током. Элемент ЧЗОС вводится в § 6.2.

В аналоговой фильтрации используются также термины: нормализован- biej. JJ денормализованные (или перенормированные ) частоты (сопротив-тя).-прим. пер.

Аналогичные результаты применительно к функциям цепи приведены в первой строке табл. 1.4-2. При использовании этих соотношений полезно помнить, что такие элементы, как сопротивление и управляемые источники, функции цепи для которых не являются функциями S, остаются инвариантными и в резульч^ате денормирования по частоте, тогда как реактивные элементы,/такие как индуктивности и емкости, которые характеризуются ф/у'нк-цнямн цепи, явно зависящими от s, изменяют свое значение., Для таких реактивных элементов изменение их значения обратно' пропорционально изменению частоты.

Таблицй 1.4-2

Влияние денормирования по частоте и полному сопротивлению, на функции цепи

В таблице а, (3, г - соответствующие коэффициенты усиления, а Л/- коэффициент трансформации.

Как пример денормирования по частоте, рассмотрим (нормированную) цепь на рис. 1.4-1,а. Передаточная функция по напря-

P,22SOeyfir О-- v-

0,ШЗЗ 10

Рис. 1.4-Денар.мярование частоты и полного сопротивления фильтра. Значения элементов схем даны в омах, генри, фарадах

жению при использовании р как переменной комплексной частоты имеет вид

yApWi{p) = N{p)=-0,6p/{p + 0,6p + 2). (2)

\ Полюсы функции цепи р = -0,3±j 1,38203. На основании материала, приведенного в § 1.3, можно заключить, что это соответствует характеристике ПФ, средняя частота которой равна 1/2 рад/с (корень квадратный из коэффициента при нулевой степени р в-знаменателе). Для формирования АЧХ, имеющей точно такую же форму, но со средней частотой 10 кГц, можно воспользоваться де-нормированием по частоте вида (1) определив постоянную денормирования по частоте Q = (2jt/1/2) 10* = 4,4429-10*. Подставляя s/4,4429-10 для р в (2), получаем денормиро'ванну;ю функцию' цепи

О,6-4,4429-10*S

-. (3>

Fi(s) s2 +0,6-4,4429-10* s + 2-(4,4429-10)2

полюсы которой s = -1,33287-10±]6,14019-10*, причем легко показать, что ее средняя частота равна 10* Гц. Применяя точно такое же денормирование по частоте к элементам цепи, показанной, на рис. 1.4-1а, получаем денормированную по частоте цепь, показанную на рис. 1.4-16, реализующую функцию (3).

Роль нормирования по частоте в процессе синтеза можно наглядно показать, если воспользоваться рис. 1.4-2. Начиная с нормированной функции цепи (крайний слева блок), можно синтези-

НормираВа-ние по частоте функции цепи j-

(Приме Л Iненив \ метода синтеза]

fНормированный по частоте фильтр

JJlEHOpMU - ч роВанный по частоте фипьтр,ло-пичениьш белением

LuCho Qn

( Функция цепи, денор-мирован-мая по частоте.

Денормиро-ванная по частоте функция цепи. N(s)

(fJp.

Применение , метода ( синтезах

Денорми -роВанныи по частоте ильтр

Рис. 1.4-2. Структурная схема для ирадставлеиня синтеза и денормирования

по частоте

ровать денормированный фильтр, следуя по любому из двух указанных путей. На нижней ветви порядок двух операций меняется местами. Следуя по любому пути, получаем один и тот же результат, однако рекомендуется использовать верхний путь, так как при этом значительно упрощаются численные расчеты.

Второй тип денормирования, который часто используют длЯ' упрощения численных расчетов, проводимых в процессе синтеза, называется денормированием полного сопротивления. Он позволяет использовать элементы, численные значения которых близки к единице, вместо того чтобы использовать фактические значения имеющие множители 10, Ю', 10 , Ю- и т. д. Нормированное-Полное сопротивление Z (s) может быть денормировано к полно-

му сопротивлению Z(s), т. е. преобразовано к практически используемым значениям с помощью соотношения

2( ) = г„2Л^). (4)

где Zn - постоянная денормирования полного сопротивления.

Для примера рассмотрим катушку, индуктивность которой пос-.ле нормирования полного сопротивления равна L генри. Нормированное полное сопротивление имеет вид Zn{s)=sL, а денорми-рованное (фактическое) сопротивление соответственно Z{s)=sZnL, т. е. соответствует катушке с индуктивностью ZnL. В то же время для конденсатора, емкость которого после нормирования полного сопротивления равна С фарадам нормированное полное сопротивление имеет вид Zn{s) = llsC, а денормированное - Z{s)~ =ZnlsC, что соответствует конденсатору с емкостью Cfzn. Таким образом, если осуществляется денормирование полного сопротивления, то значение индуктивности (в генри) увеличивается, а значение емкости (в фарадах) уменьшается. Аналогичные соотношения можно непосредственно получить и для других типов элементов, а также для функций цепи. Результаты сведены в табл. 1.4-1 и 1.4-2 (вторая строка).

В качестве примера денормирования полного сопротивления выберем Zn так, чтобы емкость конденсатора в цепи, показанной ма рис. 1.4-1,6, изменилась и стала равной 10- Ф. Из (4) находим, что 1/5-10-=г„/(5-0,11254-10-). Тогда получаем г„= 1125,4. Денормированные значения для элементов данной цепи указаны -на рис. 1.4-1,в. Так как функция цепи вида (3) для цепи на рис. 1.4-1,6 безразмерна, то указанное преобразование полного сопротивления на нее не влияет, следовательно, она также применима и к цепи на рис. 1.4-1,е. Следует отметить, что операции денормирования по частоте и полному сопротивлению (как это видно из третьей строки табл. 1.4-1 и 1.4-2) коммутативны: их можно осуществлять в любом порядке - результат будет одним и тем же.

1.5. Пример использования фильтров

Одним из интересных примеров того, как используются фильт-;ры в практических устройствах, является система кнопочного набора многих телефонных устройств. В такой системе телефон имеет группу из 12 кнопок, которые заменяют вращающийся диск. Каждая такая кнопка, будучи надавлена, возбуждает генераторы, которые одновременно генерируют и посылают в линию низкочастотный и высокочастотный звуковые сигналы. Частоты, соответствующие тем или иным кнопкам, показаны на рис. 1.5-1,а. Например, кнопка 3 генерирует частоты 697 и 1477 Гц. Таким образом, каждая кнопка идентифицируется двухтональным кодовым сигналом. На центральной телефонной станции эти сигналы деко-.дируются с помощью набора фильтров, соединенных так. как показано на рис. 1.5-1,6. Фильтры нижних и верхних частот на вхо- Де используются для разделения групп нижних и верхних частот.

770-

PRS 7

JKL 5

a полосовые фильтры - для Кнопки ноБара

идентификации определен- Частоты ных частот в каждой группе, группы Выходные напряжения полосовых фильтров КОНТрОЛИру- 657,

ются детекторами, которые путем использования простых логических схем позволяют идентифицировать ту кнопку, которая была нажата.

Такая система позволяет более быстро набирать номер, чем обычная система с вращающимся диском, в которой подсчитывается каж дый импульс постоянного тока для того, чтобы (Определить каждую цифру. Оче- git\-видно, что фильтры играют важную роль в работе системы кнопочного набора.

Опера-тар О

JJEF 3

Частоты SV группы а)

Сигнале теледт-иой

ФНЧ

Я>ВЧ

fo = 85г

п<?

fa = f203

П'Р

fo = шь

1ТФ ~, fa = по г

\fi,emei<-

Детектор

Аетек-твр

Детектор

Детектор

Детектор

Детектор

Клоеическим-схемам а переключающей системе

ПЧ>1 дополни -тельный канал

Детектор

Рис. 1.5-1. Кнопочная .система телефонного набора

1-1 (§ 1.1). Выведите выражение (3) в § 1.1 для передаточной функции То напряжению цепи, .показанной на рис. 1.1-2.

1-2 (§ 1.1). Выведите выражения (10) я (11) в § 1.1 для амплитуды и фазы шередаточной функции по напряжению цепи, показанной на рис. 1.1-2.

1-3 (§ 1.1). а) Найдите передаточную функцию по напряжению для цепи, локазавной иа рис. 1.3-3.

б) Найдите выражения для амплитуды и фазы передаточной функции.

1-4 (§ 1.2). Найдите передаточные функции по напряжению для цепей, схемы которых ианы ла рис. ЗЛ-4 и пожажите, что положение полюсов согласуется с данными табл. 1.2--1.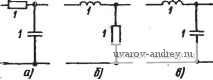

1 Ф^аОг,

Рис. 31-4. Схемы цепей к задаче 1.4. Значения элементов даиы в омах, генри,

фарадах

1-5 (§ 1.2). Найдите входную полную .проводимость (со стороны вход-;ной пары зажимов /) цепи на рис. 1.1-2, и покажите, что она имеет те же БОЛЮСЫ, что и передаточная функция .по напряжению, определенная выражением в (3) § 1.1.

1-6 (§ 1.2). Найдите входную полную проводимость (со стороны входной пары зажимов 1) .цепи на рис' 1.3-3 и покажите, что она имеет те же полюсы, что и передаточная функция по напряжению, определенная в задаче 1-3.

1-7 (§ 1.3). Амплитудно-частотные характеристики функций цепи часто изображают, откладывая по оси ординат значения затухания, а не коэффи-диента усиления. Предполагая, что это выполнено, определите, какой из графиков идеальных характеристик, показанных на рис. 3.1-7, соответствует ФНЧ, ФВЧ, ПФ и Р (режекторному фильтру).

п

Рис. 31-7. Идеальные характеристики фильтров к задаче 1.7

1-8 (§ 1.4). Цепь нижних частот на рис. 1.1-2 имеет полосу пропускания 1 рад/с для указанных значений еламентов.

а) Найдите значения элементов, которые они должны иметь в результате денормирования по частоте, необходимой для изменения ширины полосы пропускания до il кГц.

б) Запишите передаточную функцию по напряжению для такой д^енорми-рованной по частоте цепи.

в) Денормируйте шолное сопротивление так, чтобы оконечный резистор имел сопротивление 10 кОм.

г) Запишите передаточную функцию по напряжению для цепи с денорми-рованным полным сопротивлением.

1-9 (§ 1.4). а) Учитывая, что денормирование по частоте, использованное в задаче 1-8, применяется к .цепи иа рис. 1-1.2, запишите функцию входной лолной проводимости (определенную первоначально .в задачеl-) для де-нормироваиной по частоте цепи.

б) Полагая, что денормирование полного сопротивления, использованное в задаче 1-8, применено к рассматриваемой цепи, запишите функцию входного полного -сопротивления для результирующей цепи.

1-10 (§ 1.4). Цепь верхних частот, схема которой показана а ,рис. 1.1-3 имеет частоту среза 1 рад/с щля указанных номиналов элементов.

а) Найдите значения номиналов элементов, получаемые в результате денормирования ло частоте, проводимой для изменения частоты среза до 1 кГц^

б) Запишите передаточную функцию ,по напряжению для такой денормиро-ванной по частоте цепи.

в) Осуществите денормирование полного сопротивления так, чтобы оконечный резистор имел сопротивление 10 кОм.

г) Запишите передаточную функцию по напряжению для такой денорми-ровакной по частоте я полному сопротивлению цепи.

1-11 (§ 1.4). Передаточная функция по напряжению для полосовой цепи, схема которой показана на рис. 3.1-11, имеет среднюю частоту 1 рад/с и ширину полосы пропускания ОД рад/с.

Рис. 31-11. Схема цепи к задаче ZO 1.11. Значения элементов даны в Г--

омах, генри, фарадах Д£2

а) Найдите значения номиналов элементов, получаемые в результате денормирования по частоте, проводимого, чтобы средняя частота приняла значение 1 кГц.

б) Чему равна при этом ширина полосы денорм1нраванной цепи?

в) Чему равиы значения номиналов элементов, если, роме указанного проводится щенормирование полного сопротивления так, чтобы оконечный резистор имел сопротивление 1 кОм?

АППРОКСИМАЦИЯ

В гл. 4 - 7 будем рассматривать методы использования активных цепей для синтеза передаточных функций. Применяя эти методы, будем предполагать, что функция цепи, т. е. отношение полиномов, определяющее положение полюсов и нулей в плоскости комплексной частоты (или s-плоскости), задана как исходный пункт всей процедуры реализации. Однако при практическом синтезе фильтров главное внимание проектировщика сосредоточено-обычно на том, чтобы удовлетворить некоторым техническим условиям на характеристики цепи в установившемся режиме при гармоническом воздействии, т. е. на соответствующие амплитудно-частотные и/или фазочастотные характеристики как функции, зависящие от переменной вещественной частоты ш. В этой главе рассмотрим, насколько два Эти метода описания характеристик цепи соответствуют друг другу, т. е. как частотная характеристика связана с положением нулей и полюсов. Такая связь характеризуется общим термином аппроксимация.

2.1. Аппроксимация амплитудно-частотной характеристики. Максимально плоская характеристика

Наиболее часто используется тип аппроксимации, который модулю функц'ии ЛГ(]ш), определенной аналитически с помощью некоторого математического выражения, или набором данных, или, наконец, графически ставит в соответствие рациональную функцию F{s) так, что в некотором определенном смысле аппрок-

симирует Af(jtu) . Хотелось бы, чтобы в идеальном случае указанные две функции были идентичны, и в большинстве случаев мы

Таблица 2.1-1

Соотношения между значениями амплитуды в децибелах и В ли.чейной мере

Примечание. А - амплитуда.

убедимся, что это так и будет. Амплитудно-частотная характеристика (АЧХ) задается обычно либо в линейной, либо в логарифмической мере. В последнем случае в качестве единиц используются децибелы [20 lgiV(jtu) ]. В табл. 2.1 - 1 приведены соотношения между значениями амплитуды в линейной мере и в децибелах.

Изучение аппроксимации АЧХ начнем с рассмотрения необходимых свойств, которые должна иметь АЧХ. Фактически более удобно рассматривать квадрат модуля АЧХ. В этом случае можно записать

liV (j ш) 2 = iV (j to) N* (j oj) N{l&)N(-i to), (1>

причем подтверждением справедливости записи в правой частр; равенства служит то, что для рациональной функции с вещественными коэффициентами сопряженная функция находится путем замены ее аргумента на сопряженную величину, т. е. путем замены jo на -joj. Предположим теперь, что

jV( w b, + bis + b2s + bs + bis:* + ...

Тогда

ЛГ л- (Л Ьр -feg Сй -f 64 tu-- - - -Ь j (1 to -3 со + ...) /gv

йо-Ca св-f 0:4 ш*-...-f ] (ai to-Ь аз -1- )

Подставляя это соотношение в правую часть выражения (1), убеждаемся, что квадрат модуля A(jtu)P является отношением четных полиномов (первое свойство). Если теперь подставить в (1) (B=s/j, то сможем определить функцию

Т(s) = liV(j(o)\Usji N{s)Ni-s). (4)

Из выражения (4) следует, что полюсы и нули T(s) должны иметь квадрантную симметрию в s-плоскости, т. е. должны быть симметрично расположены по отношению к началу координат в правой и левой полуплоскостях. Это, конечно, является необходимым условием того, чтобы T{s) была равна произведению N{s)N{-s). В общем случае полиномы в числителе и знаменателе {5-) могут иметь только три типа сомножителей: I) s+as+b,. 2) -а(а>0) и 3) s+aiaO). Первый и второй типы сомножителей действительно имеют квадрантную симметрию, тогда как третий тин обладает ею только в случае четного числа таких сомножителей, т. е. в случае, если они имеют вид (s+a) (s-t-a)* и т. д., когда получающиеся в результате четно-кратные нули на оси jo будут иметь необходимую симметрию.

Подводя итог рассмотренному, можно сказать, что для того. чтобы данная функция A(j(o)p была квадратом модуля некоторой рациональной функции Nis) необходимо, чтобы, во-первых. Функция \N{1&)\ была отношением четных полиномов от со и, во-вторых, любые полюсы или нули на оси jo, связанной с ней функции T{s), определенной в (4), были бы четного порядка. Достаточность этих двух условий легко показать представлением