4-4 (§ 4.2). Используя расчетные соотношения (13), § 4.2, реализуйте фильтр BecceJl второго порядка с групповым временем прохождения 1 мс.

4-5 (§ 4.2). Другой метод синтеза ФНЧ на рис. 4.2-3, который позволяет удовлетворить требованиям, накладываемым на Яо, а также на Юп и Q, состоит в следующем: выберем К=Но н Ci=Ci=C, тогда

/?з = {1/2и„ QC) [1 + Vl + 4Q2 (Яо -2)1; 1/0)2 С2;?з,

где Яо>2.

Применяя эти соотношения, проведите синтез фильтра с fn=30 Гц, Q=1/A2; Яо=10 и С=0,1 мкФ.

4-6 i(§ 4.2). Выведите расчетные соотношения, приведенные в задаче 4-5.

4-7 (§ 4.2). Определите различные чувствительности в выражении (27), § 4.2, для реализации ФНЧ Саллена и Ки, показаниаго на рис. 4.2-4, в котором R=\QRi и С4=0,1С2.

4-8 (§ 4.2). Определите различные чувствительности в выражении (27), § 4.2, для реализации ФНЧ Саллена и Ки, схема которого показана на рис.

4.2-, в котором C2= l/3Q, С4=1, i?i=l/Qco , 7?з=1/( УЗсоп) и C4=l/2Qco .

4-9 (§ 4.2). Определите различные чувствительности в выражении (27), § 4.2, для реализации ФНЧ Саллена я Ки, схема которого приведена на рис. 4.2-4, IB котором C2=1/3Q, Ci=\, Ri=l/Q(u , /?з=1/(1/з'шп) и K=4l3. Считается, что эта реализация является наилучшим коморомиссом между чувствительностью активных и пассивных элементов [46].

4-10 (§ 4.3). Докажите, можно или нельзя использовать схему iJC-фильт-ра на усилителе с положительным коэффициентом уоиления для реализации комплексно-сопряженных полюсов, если установить усиление K=i.

4-11 (§ 4.3). Спроектируйте .полосовой /?С-фильтр на усилителе, используя метод, описанный в § 4.3, при условии, что проводимости реализуют следующие элементы; Yi=sCi и Уз=Оз. Получите расчетные соотношения, аналогичные выражениям (8) и (9) этого параграфа.

4-12 (§ 4.3). Еще одна процедура синтеза ФВЧ, схема которого показана на рис. 4.3-2, которая позволяет удовлетворить требованиям, наложенным на Яо, а также на Сй и Q, состоит в следующем: выберем С1=Сз=С, тогда

Ra = U/2Q + 1/2Щ;:Л)+1740 ]/2со С; = (2/сОп C)/[1/2Q + У2(Яо -I)-bl/4Q4.

Применяя эти соотношения, синтезируйте фильтр с Q=0,707, f =300 Ги и Яо=100.

4-13 (§ 4.3). ВьЕведите расчетные соотношения, приведенные в задаче 412.

4-14 (§ 4.3). а) Для схемы /?С-фильтра верхних частот Саллена и Ки, передаточная функция которого по напряжению приведена в (20), § 4.3, найдите выражения для чувствительности, аналогичные приведенным в (27), § 4.2, для ФНЧ. Используйте для ИНУН реализацию на операционном усилителе, как показано на рис. 4.2-4.

б) Используйте полученные выше результаты, чтобы составить таблицу чувствительности для первых двух вариантов, определенных в § 4.3.

4-15 (§ 4.3). Повторите предыдущую задачу для ПФ, шередаточная функция по напряжению которого приведена в (8), § 4.3, и щля варианта 1, рассмотренного в этом параграфе.

4-16 i(i§ 4.3). а) Найдите передаточную функцию по напряжению для (фНЧ с отрицательным коэффициентом усиления, показанного на рис. 3.4-2 (где K<G).

б) Полагая i?i=i?2=R3=iR и С4=С5=С, найдите расчетные соотношения для RC У1. \К\ В зависимости от и Q [ом. выражение (1), § 4.2]; найдите также выражение для Яо.

4-17 (§ 4.4). а) Используя схему фильтра, показанную на рис. 4.4-il, найдите реализацию функции цепи вида

V2 (s)/Fi (S) = Я (s2 + 1,2)/(s2 + о, 1 s+ 1).

Положите параметр т равным единице.

€) Чему равно окончательное значение постоянной Яо?

4-18 (§ 4.4). Повторите задачу 4-17 для функции цепи вида

(s)/Fi (s) = Я (s -Ь 0,9)/(s + 0,1 s + 1).

4-19 (§ 4.4). а) Повторите задачу 4-17 для схемы фильтра, показанной на рис. 4.4-3. Используйте множитель (s+1) в разложении на простые дроби.

б) Повторите задачу 4-18 для данной цепи.

4-20 (§ 4.4). а) Повторите задачу 4-17 для схемы фильтра, показаи-яой иа рис. 4.4-7. Используйте множитель (s+l) в разложении на простые лробн.

Щ Повторите задачу 4-18 для этой схемы.

4-21 (§ 4.4). а) Повторите задачу 4-17 для схемы фильтра, показанной яа рис. 4.4-8. Используйте множитель (s+l) в разложении на простые дроби, б) Повторите задачу 4-18 для этой схемы.

4-22 (§ 4.5) а) Проведите синтез активного iC-фильтра нижних частот восьмого порядка с пульсацией 1 дБ в полосе пропускания и частотой среза 20 жГц. Используйте фильтр, схема которого показана на рис 4.2-3, для каждого звена второго порядка в каскадной реализации. Используйте вариант 1, § 4.2, для определения значений элементов.

б) Повторите эту задачу, иопользуя вар'иант 2.

в) Повторите эту задачу, иопользуя вариант 3, и убедитесь в правильности соответствующих значений табл. 4.5-3.

4-23 (§ 4.5). Сделайте эскиз АЧХ ПФ Баттерворта четвертого порядка со средней частотой 1 рад/с и шириной полосы 1 рад/с, реализованного путем каскадного соединения полосовых звеньев второго порядка, в которых постоянная Яо принята равной едииице.

б) Повторите то же для каскадного соединения ФНЧ второго порядка и ФВЧ второго порядка, причем ФНЧ реализует полюсы, ближайшие к началу Координат, а постоянная Яо равна единице для обоих фильтров.

в) Повторите то же с той только разницей, что теперь ФВЧ реализует Полюсы, ближайшие ж началу координат.

4-24 (§ 4.6). Найдите частоту, на которой структура с неинвертирующим операционным усилителем, имеющим коэффициент усиления 10 и GB равным * МГц, будет иметь избыточное запаздывание фазы 10°.

4-25 (§ 4.6). а) Найдите значение избыточной фазы для неинвертирующего усилителя с коэффициентом усиления 10, когда (в = ОВ/100.

б) Повторите т^sжe для co = GB/10.

в) Повторите сделанное в п. а) и .6) для инвертирующего усилителя с коэффициентом усиления -10.

4-26 (§ 4.6). Найдите максимальную частоту, на которой запаздывание фазы, вызванное усилителем, использованным в схеме ФНЧ с отрицательным коэффициентом усиления (см. задачу 4-16), будет меньше 10°, если GB= = 1 МГц и Q=4.

4-27 (§ 4.6). а) Найдите величину избыточной фазы, которая создается инвертирующим усилителем с единичным усилением на частоте со=0,01 GB. i6) Повторите то же для со=0,1 GB. 4-28 (§ 4.7). Выведите выражение (9), § 4.7.

4-29 (§ 4.7). а) Найдите модуль 15 дв для реализации ФНЧ, в которой используется усилитель с положительным коэффициентом усиления Q=10, 71= 10 кГц, а GB операционного усилителя равно 1 МГц. Предполагается, что используется процедура, описанная в § 4.2 для равных номиналов сопротивлений резисторов и емкостей конденсаторов (вариант 1).

б) Найдите фактическое положение полюсов фильтра, рассмотренного выше, и вычислите фактические значения Q и f .

в) Повторите проделанное выше для случая, когда fn=50 кГц.

4-30 (§ 4.7). а) Используя табл. 4.7-1, найдите jSPjcgl для полосового i/C-фнльтра на усилителе с положительным коэффициентом усиления, если Q=10, 71=10 кГц GB операционного усилителя составляет 1 МГц. Предполагается, что используется процедура, описанная в § 4.3, для равных номиналов сопротивлений резисторов и емкостей конденсаторов (вариант 1).

б) Подтвердите правильность выражений, приведенных в табл. 4.7-1, для ISPj-ggl и D(Sn) для этого фильтра.

?С.ФИЛЬТРЫ НА УСИЛИТЕЛЯХ. ЧАСТЬ 2

В предыдущей главе были рассмотрены /?С-фильтры на усилителях, причем главным образом фильтры, в которых в качестве усилителя использовался ИНУН, имеющий относительно низкий коэффициент усиления, обычно в диапазоне от 1 до 5. В этой главе проанализируем другие типы фильтров с усилителями, и, прежде всего, фильтр на усилителе, в качестве которого используется ИНУН с бесконечно большим, в идеале, коэффициентом усиления, т. е. операционный усилитель. Фильтр с таким усилителем в качестве активного элемента будем называть фильтром с бесконечно большим коэффициентом усиления, где слово бесконечный, конечно, относится к коэффициенту усиления активного элемента, а не к коэффициенту усиления схемы в целом. Такой тип фильтра имеет как преимущества, так и недостатки, если сравнивать его с теми типами, которые рассматривались в предыдущей главе.

5.1. Фильтры на одном усилителе с бесконечным коэффициентом усиления

В этом параграфе рассмотрим, прежде всего, два типа фильтров с бесконечным коэффициентом усиления. Чтобы получить первую структуру фильтра, рассмотрим схему на рис. 4.1-3. Ее передаточная функция по напряжению приводится в (5), § 4.1. Из этого выражения, полагая, что К стремится к оо, получаем

F2(s)/Fi(s)=- /3i(s)/ /3a(s). (1)

Теперь можно определить первую структуру фильтра на одном усилителе с бесконечным усилением, если преобразовать общую схему пассивной цепи к виду, показанному на рис. 4.1-4. Заменив теперь схему ИНУН операционным усилителем, получим структуру на рис. 5.1-1. Для этой схемы, используя (10) и (И), § 4.1, находим следующую передаточную функцию по напряжению:

У2 (S) = -N {s)IN {s) = Гз/[Ге (F-f + Y, + Y,) + У3].

Заметим, что У4 не появляется в выражении (2). Причину этого легко увидеть в самой схеме на рис. 5.1-1. Так как напряже- ие на входных зажимах операционного усилителя в идеале рав-

Рис. 5.1-/. Общая структурная схема фильтра с мвогопетлевой обратной связью на усилителе с бесконечным коэффициентом усиления

Рис. 5.1-2. Схема ФНЧ с многопет-левой обратной связью на усилителе с бесконечным коэффициентом усиления

НО нулю, ясно, что напряжение на элементе У4 отсутствует, следовательно, этот элемент можно удалить, и это никак не повлияет на передаточную функцию данной цепи. Так как существзтот две петли обратной связи (замыкающиеся через элементы Уг и Уе) с выхода операционного усилителя к пассивным элементам цепи, то этот тип фильтра называют обычно фильтром с многопетлевой обратной связью. Сравнивая (2) с общей формой различных передаточных функций второго порядка, рассмотренных в § 4.2 и 4.3, можно получить различные типы реализаций фильтров.

В качестве первого типа фильтра рассмотрим ФНЧ, имеющий функцию цепи вида (1), § 4.2. Сравнивая ее с (2), замечаем, что

у, = Gi и Уз=Сз. Знаменатель (2) можно поэтому переписать в виде

D(s)Y,(Gi + Y+Gs + Y)+YG,. (3)

Чтобы этот полином был второго порядка, необходимо принять, что Yi=G2, Y5=sC5 и Y6=sCe. В итоге получаем реализацию ФНЧ, показанную на рис. 5.1-2. Ее передаточная функция

V2m\{s)-GMsCCe + sC,iGi+G + Gs)+G2G,]. (4)

Ее можно представить в виде

VAs) -\/RiRsC,Ce

Vl (5) + s (I/Cb) (1/Ri + 1/?2 + I/R3) + l ?2 3 Cfi Ce

Сравнивая (5) с (1), § 4.2, получаем следующие соотношения:

о)п = 1/У'теад; (6а)

1/Q=Vc;Ic;{VR/Ri+VrM+VrM); (бб)

Процедура синтеза, позволяющая выбрать стандартные номиналы емкостей конденсаторов, состоит в следующем: Дано: Но, Q и &п-Выбираем: Съ = С (для удобства). Вычисляем

С.тС; m<l/4Q2(l + ol); (7о)

/?2 = (1/2со СmQ) [ 1 ±Kl-4mQMl + lol)]; (76)

Ri=R.J\Ho\, Rs=\/(ofCRtn. (7в), (7г)

Другой подход, который можно использовать при синтезе активного ФНЧ с бесконечным усилением, приведен в задачах.

Пример 5.1-1. Фильтр нижних частот с многопетлевой обратной связью на одном усилителе с бесконечным коэффициентом усиления. Пусть требуется реализовать фильтр нижних частот Баттерворта второго порядка (Q=0,7071), для которого / =сй /2я=100 Гц и Яо = 1. Используя процедуру синтеза (7), выбираем С5 = С=0,1 мкФ. Так как из выражения (7а) следует, что т должно быть меньше, чем 1/4, выберем т=0,1, поэтому Сб=С/10=0,01 мкФ. Затем находим i?,=J?2= 199,7 кОм и J?3= 12,68 кОм.

Одно из основных Преимуществ фильтра с многопетлевой обратной связью на одном усилителе с бесконечным усилением состоит в низкой чувствительности фильтра к изменению значения элементов схемы. Используя определения, введенные в § 3.5, а также (6), получаем

=Q{l/Ri) VRRCJcI; (8а)

SS.--S8.= l/2; S- = C; (Sr), (8д)

Различные члены, заключенные в скобки в выражениях для чувствительности добротности к Ri, R2 и Ръ, меньше по модулю, чём выражения для 1/Q, приведенные в (66). Следовательно, произведение добротности на любой из этих членов в скобках должно быть по модулю меньше единицы. Отсюда делаем вывод, что

<1/2.

1; 5J<i/2;

Чувствительность этой схемы к коэффициенту усиления усилителя также должна быть меньше (и это легко показать), чем величины, приведенные выше [13]. Таким образом, эта схема обеспечивает крайне низкую чувствительность, причем предельные значения не зависят от Q. Аналогичные выводы можно получить и для ПФ и ФВЧ, основанных на этой схеме. Они будут рассмотрены ниже в этом параграфе.

Интересно исследовать схему на рис. 5.1-2 более подробно. Из выражения (1) ясно, что нули передаточной проводимости /32(5) создают комплексную пару полюсов передаточной функции по напряжению в целом. Для определения t/32(s) необходимо, чтобы зажим 1 на входе был заземлен. Полученная в результате пассивная /?С-цепь показана на рис. 5.1 -3. Заметим, что она не яв-

т

3 -о

Рис. 5.1-3. Определение j/32(s) для пассивной цепи на рис. 5.1-2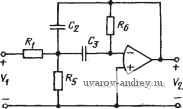

Рис. 5.1-4. Схема ПФ с мво--гопетлевой обратной связью на усилителе с бесконечным коэффициентом усиления

ляется лестничной цепью. По существу, нули передаточной проводимости короткого замыкания yz2{s) могут располагаться в любом месте левой полуплоскости комплексной плоскости. Фактически же данная цепь является просто хорошо известной мостовой 7-образной схемой с дополнительным резистором R. Эта же конфигурация является одной из тех, что формируют комплекснЬш собственные частоты во всех типах фильтров с многопетлевой обратной связью, рассмотренных в этом параграфе. -

Второй фильтр с многопетлевой обратной связью и бесконечным усилением, который здесь будет рассмотрен, является полосовым фильтром, имеющим функцию цепи вида(!),/§ 4.3. Из выражения (2) следует, что существуют два возможных варианта реализации этой функции. Рассмотрим сначала один из них, когда Yi = Gi и ¥з=8Сз. В этом случае знаменатель (2)

D (S) = Y, (Gi -t- Уа + S Сз -t- П) -t- Га S С3. (10)

Для того чтобы D{s) была второго порядка, примем: Y2=sC2, ¥5=05 и Ye=Ge. Полученная в итоге реализация приведена на рис. 5,1-4. Ее передаточную функцию

Vs{УУгis)- -SGiСз/[в^CC + s(G, Q +G,Q +Ge(G + G,)] (11)

можно переписать в виде

Vti ) -s/Ri С2 ,j2)

Сравнивая (12) с (1), § 4.3, выводим следующие соотношения: п = + Rb/Rif VR, Re Q (13a)

...... 1/Q = (V /?б CRe Сг -f VRb Cs/Re / Vl + Rb/Ri\ (136)

1о1=(ад)/(1+Са/Сз). (13в)

П()оцедуру синтеза можно получить, подставляя С2=Сз=С; тогда

;?1--=(3/со С|Яо1; (14а)

/?5 = еда-Яо1)со С; (146)

/?6 = 2<3/со С. (14в)

В литературе уже появился набор номограмм, позволяющих найти значения R в соответствии с (14) [47].

Пример 5.1-2. Полосовой фильтр с многопетлевой обратной связью на одном усилителе с бесконечным усилением. Пусть требуется реализовать ПФ второго порядка, для которого На-2, Q=2, (о„ = 10 крад/с.

Если выбрать С2=Сз=С=0,01 м Ф, то из (14) находим: /?i=10 кОм, i?6=3,33 кОм и /?б=40 кОм.

Можно исключить Rz из схемы на рис. 5.1-4, сохранив тем не менее полосовую реализацию. Однако, если сделать это, то Яо уже нельзя рассматривать как свободный параметр. Например, если С2=Сз и i?,= oo, то вместо (136) и (13а) получаем

т=2УЩ1я,- (15а)

Яо=/?в/2/?1. (156)

Таким образом, o=2Q2. При больших значениях Q модуль Яо будет очень большим. Это нежелательно, так как, если аналогичные каскады включаются последовательно, то общий коэффициент усиления может быть слишком велик, а следовательно, до-

-пустимый уровень сигнала и устойчивость пол)Д1енного в результате фильтра будут значительно снижены. Если выбрать Yi = sCi и Уз=Сз, то придем к другой возможной реализации ПФ. Эта реализация требует трех конденсаторов, вместо двух минимально необходимых в реализации, описанной выше. В качестве упражнения читатель может получить необходимые расчетные соотношения.

Последней реализацией, которую рассмотрим в этом параграфе как реализацию фильтра с многопетлевой обратной связью, будет ФВЧ, передаточная функция которого приведена в (16), § 4.3. Применяя данные табл. 4.3-1 для преобразования ФНЧ-прототипа на рис. 5.1-2, получаем в результате о-

Рис. 5.1-5. Схема ФВЧ с,многопетлевой обратной связью -на усилителе с бесконечным коэффициентом усиления

фильтр, схема которого показана на рис. 5.1-5, где Yt=sCi, У2 = = С2,Уз = 5Сз, Ys = G5 и Уб = Сб. Его передаточная функция

Ее можно представить в виде

(16)

(17)

Заметим, что требуются три конденсатора, т. е. полученная реализация неканоническая. Приравнивая (16) и (.17), получаем

(18а)

(186) (18в)

® = 1/] ?5бС2Сз;

1/Q - VRjRe (С1/1/СЙ+Vcjc+Vcjcy,

\H \Ci/C.

Набор расчетных соотношений можно преобразовать к более удобному виду, полагая, при этом €1 = 63=С, где С выбирается из конструктивных соображений. В результате получаем

R,= \Homw QC{2]Ho\ + l)]; /?б = (2ЯоЦ-1)0/со С; Q = C/o.

(19а) (196), (19в)

Пример 5.1-3. Фильтр верхних частот с многопетлевой обратной связью на одном усилителе с бесконечным усилением. Пусть требуется реализовать .передаточную функцию Баттерворта второго порядка (Q=0,707) для ФВЧ, где if =cu /2n=100 Гц и Яо = 1. Выбрав С=С,=Сз=0,1 мкФ, найдем, что С2=0,1 1мкФ, i?6=7,503 кОм и J?6=33,757 кОм. ф ..

Вторая структура фильтра на одном усилителе с бесконечным коэффициентом усиления, которая будет здесь рассмотрена, это

структура с однопетлевой обратной связью [48, 49] (рис. 5.1-6).

Цепи А Vi. В являются пассивными /?С-цепями с параметрами /°tj(s) и yiji.s). Анализ схемы показывает, что так как напряжение, приложенное к узлу <?, равно нулю и ток, текущий в операционный усилитель, равен нулю, то

h (.s) = - УЧ, (S) \\ (S); 4 (S) = -у% (S) Fa is).

(20)

Так как Ia{s)=-his), то передаточную функцию можно пред-

ставить в виде

VAs)n\{s)=-y°{s)/yl{s). Цепь в

(21)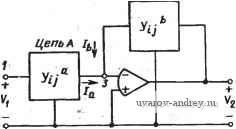

£ Рис. 5.1-6. Общая структурная схема фильтра с однопетлевой обратной связью на усилителе с бесконечным коэффициентом усиления

Передаточные проводимости короткого замыкания в (21) можно выразить через соответствующие полиномы их числителей и знаменателей:

y 2{s) = Nb{s)llfi2{s)\...y\2{s)N\2{s)ldi2{s). (22)

Подставляя эти выражения в (21), получаем

12 тг (S) = -N,2 {S) D?2 (S)/M2 (s) £>?2 (s). (23)

Предположим теперь, что пассивные цепи выбраны так, что полюсы y i2(s) и y\2{s) совпадают; тогда Z)i2(s) сокращается с D i2(s), в результате (23) упрощается:

{sWi (s) = -NI2 {s)/N\2 (s). (24)

Так как они являются числителями передаточных функций RC-neneu, то №12(5) и N>\2{s) могут иметь комплексно-сопряженные корни. Следовательно, в (24) могут быть реализованы как комплексные полюсы, так и комплексные нули. Данные об основных цепях реализующих различные / i2(s) и y\2{s), приведены в табл. 5.1-1 [27]2.

Метод реализации передаточных функций, использующий выражение (21), называют иногда методом одиночной инверсии, см. работу [2*]. - Прим. пер.

Более подробные таблицы схем с передаточными проводимостями короткого замыкания можно найти в работе: Н. Н. Слепов. Синтез фильтров по методу одиночной инверсии для систем анализа вибраций. - В кн.: Вибрации механшмов с зубчатыми передачами. М.: Наука, 1978, с. 89-98. - Прим. пер.

Таблица 5.1-1

Пассивные jRC-цепи, пригодные для реализации Уцв) и yhjis)

Схема ЛС-цепи

Передаточная полная проводимость

У12 =

- ks S + C

Значения элементов в омах и фарадах

RC

- k s+ a

.; a=

R1R2 С' ~ С Ui Rt )

о-i--о

У12 =

-ks s+a

и 12 1

Ci+Q i?(C,+Cg)

-(s + fls+l)

s-\-a l/2<a<2

i?i = 1/(2,5-a); Ci=l; <?2 = l ?ii?2

f/l2=-

(s+l)(s2+as+l)

(S + 0l)(S+02)

a<\

= (2,5-a)

1 + a

2 + a

C2 = l ?2 = C,/(Ci-l); C3=l ?3=Ci Ca/(l+a)

Передаточные проводимости каждой из этих цепей также приведены в таблице. Первые три цепи обеспечивают нули передачи в начале координат или в бесконечности, поэтому их можно использовать для реализации числителей передаточных функций нижних частот, верхних частот и полосовых. Передаточная полная проводимость каждой из этих цепей содержит в знаменателе член вида (s+g), который должен сокращаться с подобным членом в знаменателе передаточной полной проводимости цепи В. Четвертая и пятая цепи полезны для реализации комплексных корней, как в числителе, так и в знаменателе передаточной функции по напряжению всей цепи в целом. Четвертая цепь является Т-образным мостом, который можно использовать для реализации низко-