получаем характеристики, показанные на рис. 4.6-5. Аналогичные характеристики для режима большого сигнала здесь не приводятся только потому, что они более сложны, чем соответствующие характеристики инвертирующего усилителя [43].

ю

-I-I-I I I I

т-I I I I

J-Т ) Т Т I f

Ш OfiZ 0,03 O.Ot 0,05 0,07 0,t

* CUJGB

a)

B,Z 0,3 П,и 0,5 0,1 l,B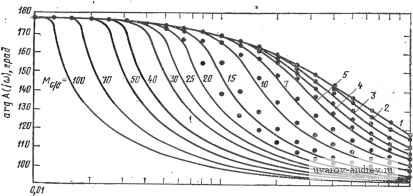

B,DZ 0,03 0,0t 0,05 opi 0,1 0,Z B,3 0,it 0,5 OJ /,в

gj си/ев

Рис. 4.6-4. Искажения в режиме большого сигнала для инвертарующего усилителя с единичным усилением

Избежать появления указанных искажений в режиме большого сигнала можно, либо выбрав операционный усилитель с более высокой скоростью нарастания, либо предохранив усилитель от такого нарастания. Операционные усилители с полевыми транзисторами на входе имеют не только более высокую скорость нарастания, но и большее значение 6, чем усилители с биполярными транзисторами. Операционный усилитель можно предохранить от чрезмерной скорости нарастания, предотвратив чрезмерное превышение

f) сигналом Vi. Однако это решение обходится слишком дорого, так как избыточное нарастание появляется тогда, когда амплитуда входного сигнала превышает уровень 6 и когда наклон выходного сигнала превыишет SR. К сожалению, когда амплитуда входного сигнала больше 6 и наклон выходного сигнала меньше, чем SR, то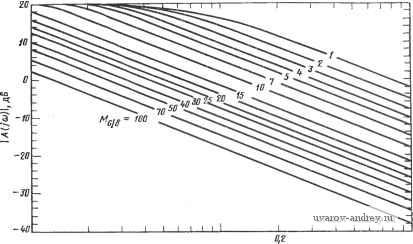

uj/ев с)

0,3 0,4- 0,5 Ц7 1,0

в,вг 0,03 орч 0,05 ofii aj

0,1 0,3 0,f 0,5 0,1 1,0

Рис. 4.6-5. Искажения в режиме большого сигнала для инвертирующего усилителя с коэффициентом усиления 10

избыточного нарастания не происходит, и оказывается, что нет необходимости ограничивать входной сигнал. Более удачным решением было бы установить перед операционным усилителем схему, ограничивающую скорость нарастания до величины, при которой наклон на выходе усилителя еще не превышает значения

SR [44]. К сожалению, такие ограничивающие схемы сами вносят дополнительные искажения фазочастотной характеристики. Во многих случаях при синтезе фильтров разработчику необходимо найти скорость нарастания, которая является предельной для данной реализации.

4.7. Чувствительность частотно-зависимых параметров цепи

В этом параграфе рассмотрим новую концепцию в анализе чувствительности, а именно: чувствительность частотно-зависимых параметров цепи. При реализации активных фильтров такая зависимость характерна для коэффициентов усиления активных элементов цепи. В частности, операционные усилители, используемые для синтеза таких цепей, являются дифференциальными и характеризуются известной моделью коэффициента усиления с доминирующим полюсом

Ad(s)=G5/(s+a) ) = A o) /(s-fo)), (1)

где Ао - коэффициент усиления по постоянному току, Оа - ширина полосы, а GB - произведение коэффициента усиления на ширину полосы, или ширина полосы единичного усиления. На частотах выше, чем Wa, (1) принимает вид

Aa{s)==GB/s. (2)

В этом параграфе исследуем чувствительность полюсов цепи к изменению GB. Больше всего для такого исследования подходит относительная чувствительность комплексных корней

р. \dPilPi 1 dPi /дч

° дСВ/Св piGB d{\IGB)*

где Pi - положение одного из полюсов передаточной функции цепи. Эту чувствительность будем далее называть частотно-зависимой.

Рассмотрим теперь общий метод вычисления SPiOB- Для случая, когда Ad(s) можно представить выражением (2), знаменатель D(s) JC-реализации на усилителях можно записать в виде следующего степенного ряда:

D (S) Ро (S) + Pi [s) {s/GB) + Р, (s) {s/GBf -f(4)

где коэффициенты Pi(s) ряда суть полиномы от переменной комплексной частоты S. Если оставить только первые два члена разложения, то

D{s)P is)-{s/GB)Pi{s). (5)

Полученное выражение можно переписать в виде

где k, Цъ q\ и Qu являются функциями сй , q и параметров реализации. Очевидно, что как только GB стремится к бесконечности, i?(s) стремится к виду, стандартному для знаменателя передаточной функции второго порядка. Используя методику § 3.4 и (5), можно получить

д {IIGB) dD (s)/ds

-sPjjs)

Pt dPQ(s)/ds sp Более удобная форма (7) имеет вид

dGB \GB ) д (l/GB) \GB )

dPe{s)/ds s=Pf

Применяя результаты в (8) к (6), получаем

dpi -

2kGB I Q

/ Я2

dGB 2fe l/(4(2a-1)GB2

Эти уравнения можно упростить путем замены

Тогда выражения (9) принимают вид

Re {dpildGB) = (-4>j2kGB){x/Q ~ у);

Im (dpi/dGB) (-(ol/2kGBYW) ix/Q-2x-y). Подставляя их в (3), получаем

(7) (8)

(9б>

(10)

(11а) (116)

\2kpiGB)

Так как /?i = (to72Q)(-l-bJT/4Ql),

(12)

то можно показать.

что

S/= (© даОВ) [~х+\(2Q2 y-x)iyW=].

(13>

Вещественную и мнимую составляющие (13) тогда можно выразить в виде

neSi==-anX/2kQGB;

(14а>

Im = © (2(2 y-x)/2k QGBVWh im

Решая эти уравнения относительно S и Sgb и используя (12), § 3.5, получаем

S$B = 1 )/4<2] (Im S- Re Sg); (15a>

( Se;n = ReSeJ/4Q2-b[(4Q2-l)/4Q2] (imS) (156>

(тот факт, что в этих соотношениях используется нормированная -чувствительность корней, не играет роли).

Другой полезной мерой чувствительности является значение -квадрата модуля SPiqb. Она особенно полезна при минимизации частотно-зависимой чувствительности, которая будет проведена ниже. Квадрат модуля Spxcb

\Sf-H/kGB4Q-l)] {x-xy+Qy, (16)

где X VI у определяются из (10).

Частотная зависимость реализаций на одном усилителе находится путем определения коэффициентов bi и q, как описано в (10), §4.1

b,s + biS+boY,(Yi + Y + Y,-\-Y,) + Y,Y,; (17а)

s2+CiS+c = (F3 + n + ye)(Fi + F, + K,)+K3(F, + n). (176)

Усилитель, используемый в реализациях на одном усилителе с конечным коэффициентом усиления, можно изобразить, как показано на рис. 4.7-1. Коэффициент усиления A{s) легко находится, если его представить в виде

т = V, {s)/Vi (S) = 1/11/А, (S) +1/(1 + /Cl)], (18)

где Ki определяет отношение сопротивлений резисторов, как показано на рис. 4.7-1. Амплитудно-частотную характеристику операци-..о онного усилителя можно представить в рамках + этой модели, если использовать (1) для выражения Ad(s). В результате получаем

v.- П' ° A{s)=1/[s/(GB)+ga]; (19)

где oa = 1/Ло +1/( 1 +i). (20)

Рис. 4.7-1. Схема не- Общая передаточная функция по напряже-гинвёр-гирующего уси- нию ДЛЯ реализации с одним усилителем вида

VAs)

(И).§4.

-. (21)

Vl (S) [С2 S+C-iS+ с,)/А (S)] - (б2 s2 -f fct S -f bo)

Подставляя (19) в (21) и полагая qi=Ci (г=0, 1, 2), получаем

V2is)\ YiY,

Щ (S) (<?2 s2 -f 91S-f qo) + (s/GB) (q s + qiS + <?o) - (*2 s + biS + bo)

(22)

.Последнее выражение можно переписать в виде

V2 is) Vi(s)

(oq-b)

a Яе-Ьо

a 92-2

При GB, стремящемся к бесконечности, имеем

lim Ь(± =-УгУеКо..-Ь.)

- I/ Г / vl 9l-1 rr.n--А.

GB- oo Vt (S)

, <l4 9o -to

Сравнивая полученное выражение со стандартной формой функции цепи второго порядка, видим, что

(ол Чо-Ьо)/{<Уа q-b); (25а)

(inlQiPAq-biVipAq-h)- (256)

Числитель такой стандартной функции будет иметь ви;:

для ФНЧ:

для ПФ для ФВЧ

Яо=Г1Уз/(ал9о-&о)1; (26а>

sH,= \YYAoAq-bd\; (266)

Яо =-1 Fi ал йа) I (26в)

Чтобы упростить (23), определим

! =04 92-&2- (27)

Г Тогда знаменатель (23) запишется как

D{s)k (s+сй slQ + 2) + s (92 + 9i s + 9o)/G5, (28)

что соответствует форме, приведенной в (6).

В качестве иллюстрации применения результатов, рассмотренных выше, исследуем реализацию ФНЧ, определенную выражением (10), § 4.2. Для этого, используя (17), находим

bs + bs + bosCG; (29а)

., <72S + 9iS + % = s2(C2Q) + s(C2G3 + QGi-bC4G3) + GiG3. (296)

. Из (20) и (27), учитывая, что 2 = 0 и Ло> (l-b/Ci), получаем

k = Gq2~b20Aq; a l/(l+/Ci), (30>

а из (25), так как и Ьо=0,

=?о/?2; (jQ=qiiq2-bi/GAq2- (31>

Преобразуя это выражение, находим

qoKq, ?2-(Q/ n)?i=-(Q/to )(Va)- (32)

Подставляя полученное в (10), имеем

x==~QbJ(o GA; у = 0. (33)

Квадрат модуля чувствительности корней функции по отношению к GB (16) будет теперь определяться следующей величиной:

Si Г = GB (4Q-1)] фМК (34)

Извлекаем квадратный корень из обеих частей равенства: GBy4Q-ll\RsCjV4<?-l

тде Но+1+Ki. Для варианта синтеза, использующего равные номиналы сопротивлений и емкостей (вариант / § 4.2), это дает

I si I - (Q/VWi) {Щ ijGB). (36)

Было бы интересно с этой точки зрения проиллюстрировать, как Pi зависит от частотной характеристики операционного усилителя, используя для этого графические средства. Чтобы сделать это, найдем траектории полюсов данной функции цепи при измене-:яии ОБ. Прежде всего перепишем (28) в виде

D (S) = {sVGB+s [OA +{l/GB) (co /Q + bJOA q)] +

+ S (OA co JQ + 02/G5) + OA co}. (37)

,Для варианта /, как он был определен в (14), § 6.2, имеем Оа = 1/К = Q/{3Q- 1) = 1/(1 + Ki); bJoA д., = 3 o -cu /Q. (38) В результате (37) принимает вид :(s) = iq/GB) + [Зю +GBQ/{3Q- 1)] -f s [ю^ + G5o /(3Q-1)] -f

+ OBQ(ol/i3Q~l)}. (39)

Нормируя на величину co , так что s = s/ft) и Вп=СВ/а)п, можно переписать (39) следующим образом:

( ) = -- [3 Ч- G5 Q/(3Q-1)] -Ь sjl-f GBjm-1)] -f

+ G5 Q/(3Q-1)}.

(40)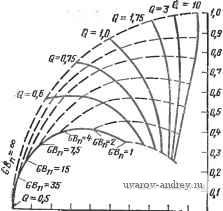

~I,B-0,Я -OJB-OJ-BJB-OJS-Ofi -0,3-0.1 -B,f a

Вычерчивая траекторию полюсов в верхней полуплоскости как функцию GBn и используя Q как параметр, получаем траектории, показанные на рис. 4.7-2. Эти кривые наглядно характеризуют влияние GB на рг [45].

Рис. 4.7-2. Влияние GB на положение полюсов ?С^фильт-ров Саллена и Ки нижиих и верхних частот второго по-ря1дка с равными номиналамя сопротивлений и емкостей (вариант 1, § 4.2 а 4.3)

Пример 4.7.1. Определение фактических значений (й„ и Q фильтра нижних частот на усилителе с конечным коэффициентом усиления. Требуется найти фактическое значение Шп и Q для реализации ФНЧ на усилителе с конечным коэффициентом усиления, вариант 1, § 4.2. Желаемые (й„ и О^авнш соответственно 100-2л крад/с и I. Значение GB равно 1,5 МГц, а частотная., характеристика усилителя имеет форму, описываемую выражением (1). Нормированное значение СВ равно 15. Из рис. 4.7-2 фактическое положение, нормированных полюсов соответствует следующим значениям: a ±JP7i=-0,4± +j0,78. Используя эти результаты, можно вычислить

tun НОРМ = к а2 -f р2 = 1/0,42 4- 0,782 = 0.876 рад/с; Q = и„ норм/2а„ = 0.876/2 (0,4) = 1,096. Поэтому фактически значения Шп и Q составляют 87,6-211 крад/с и 1,096,. В этом случае отклонение достаточно .мало, чтобы легко можно было пересчитать соответствующие значения. Для некоторых реализаций, однако, такукт-. йодстройку трудно осуществить, ф

Анализ других вариантов реализаций фильтров на усилителях, с положительным конечным коэффициентом усиления легко осуществить, следуя методике, описанной выше. Результаты некоторых таких исследований приведены в табл. 4.7-1. Сдвиги полюсов;. Pi в приведенных примерах показаны на рис. 4.7-2 - 4.7-4. Эти сдвиги можно непосредственно связать с запаздыванием фазы вызванным использованием неинвертирующего усилителя. Запаздывание фазы анализируется в § 4.6. В частности, в (46), § 4.6,.. показано, что как только GBn достигает значения, равного единице, запаздывание фазы становится большим. Однако, так как мо--дуль передаточной функции для реализации на усилителях с по-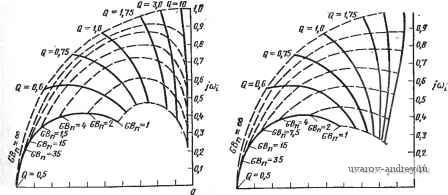

-1,в -0,3 -0 -BJ -afi -B,s -Bjt -в.з -o,z -e,i

~l,0 -BJ3 -Bfi -0,7 -0,6 -Bfi -В,Ч -0,3-B,Z -0.1

Рис. 4.7-3. Влияние GB на положение полюсов ?C-фильтplOв Саллена и Ки нижних и верхних частот второго порядка на усилителе с единичным усилением (вариант 2, § 4.2 и 4.3)

Рис. 4.7-4. Влияние GB на положение полюсов полосового iC-фильт-ра Саллена и Ки второго порядка с равными номиналами сопротивлений и емкостей (ва,риант 1, § 4.3)5

Сводка выражений для вычисления частотно-зависимой чувствительности для реализаций с положительным коэффициентом усиления

Вид реализации с положительным коэффициентом усиления

Ограничение

ФНЧ

(рис. 4.2-3)

(рис. 4.3-1)

ФВЧ

(рис. 4.3-2)

Нет

(рпс. 4.7-2)

= i?3/i?l=l

(рис. 4.7-3)

Нет

,Рс, Q {Я\(Оп\ 1 А^Гс:

\ 920 f 3 ,{o,nQ \ 2,1 \ ,

GBnQ 3Q-1

({n+{GBn+- + 2Q)sl+[l+-)sn + GBn

,Pi, (l+/<:i)eCOn (Ri \

Ri=-R2=Ri=R; Сз=Сб=С (рис. 4.7-4)

/ , , GBn \ . GBn Q 1

Нет

R2=Rl=R; Ci = C3=C (рис. 4.7-2)

-4Q-1 [ GB jy-RTCt

D (s ) - TO же, что и для случая ФНЧ с одинаковыми R яС

А=Но=1; n=RilR2=l; m= (рис. 4.7-3)

D(Sn) -то же, что и для случая ФНЧ с единичным усилением и /2=1

ложительным коэффициентом усиления при разомкнутой петле обратной связи никогда не превышает единицы, это не может привести к тому, чтобы реализация стала неустойчивой.

4.8. Выводы

В этой главе были рассмотрены ?С-фильтры на усилителях.. В § 4.1 была представлена общая структурная схема фильтра на. одном усилителе. Эта схема использовалась для реализации функций фильтрации нижних частот в § 4.2 и верхних частот и полосовых в § 4.3. Было приведено несколько вариантов процедур синтеза для каждого типа фильтра. Чувствительность таких реализаций, как было показано, должна быть относительно высока, следовательно, в общем случае они полезны только для реализации, низкодобротных звеньев фильтров. В § 4.4 обсуждались реализации функций цепи с комплексно-сопряженными нулями и полюсами, были представлены реализации, использующие один или два., усилителя с конечным или бесконечным коэффициентом усиления-Реализации фильтров более высокого (чем второй) порядка обсуждались в § 4.5. И, наконец, в §§ 4.6 и 4.7 исследовалось влияние ограничений, вносимых операционным усилителем, на характеристики ?С-фильтров с усилителями в области высоких частот.

В следующей главе рассмотрены некоторые дополнительные-структуры iC-фильтров на усилителях.

4-1 (.§ 4.1). а) Найдите полиномы, определенные в (10) § 4.1: Nsi(s),., N32(8) и N3i(s) для цепи на рис. 3.4-1. Считайте, что все пассивные элементы имеют .значение, равное единице.

б) Камим должен быть ИНУН - инвертирующим или -неинвертирующим, --для того чтобы с помощью этой схемы можно было реализовать комплеконо-сопряжеиные полюсы передаточной функции по напряжению.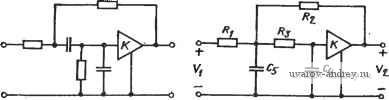

Рис. 3. 4-1. Схема фильтра задачи 4.1

Рис. 3. 4-2. Схема фильтра задачи 4.2

4-2 (§ 4.1). Решите задачу 4-I для цепи на рис. 3.4-2.

4-3 (§ 4.2). Повторите вывод, определяющий структуру ФНЧ с положительным коэффициентам усиления усилителя, .приведенный в § 4.2, полагая при этом, что в (10), § 4.1 6о¥=0, fci¥=0 и 2=0.