схема может быть расположена где-то внутри каскадной реализации; в этом случае необходимо использовать развязывающий усилитель.

Второй возможный путь, пригодный для случая, когда реализуется функция нечетного порядка (за исключением случая, когда порядок равен единице), состоит в использовании одной активной RC-cxeuu Саллена и Ки третьего порядка для реализации как отрицательного вещественного полюса, так и комплексно-сопряженной пары полюсов. Такая схема показана на рис. 4.5-3 [16]. Чтобы схема была практичной, емкости всех конденсаторов выбраны равными нормированной величине - единице, как и показано на схеме. Тогда передаточная функция по напряжению

Уг (Д) К

Vi (S) Ri /?2 Rs + [2 Ri Rs + RiR2 + R2 Rs (2-/C)] s-f [/?1-Ь^?з+(?2+?з) X

-. (5>

Чтобы определить сопротивление Ri и коэффициент усиления К неинвертирующего ИНУН, заметим вначале, что для передаточной функции нижних частот по напряжению третьего порядка, имеющий вид

(s)/Fi (s) = H/{asS + as + a,s+ 1). (6)

можно написать следующие расчетные соотношения:

aRiRRs; (7а>

a=2RiRs + R2Rs + RiR{2~К); (76)

ch = Ri + R3 + iRi + R.)i2-K). (7в>

Решение этих уравнений можно получить, используя численные ме-

тоды. Как пример, на рис. 4.5-4 показан ряд таких решений при различных значениях К для функций Баттерворта третьего порядка (аз = = 1, G2 = 2, ai = 2). Из рисунка видно что решение существует для диапазона изменения К, равного приблизительно 1,86... 2,99, хотя требуемые значения сопротивлений, особенно на краях диапазона, имеют очень большой разброс. Особый интерес J представляет решение при К=2, т.е. 2. 2,5 J при таком значении коэффициента

Усиление, К усиления, который, как было показа-

но выше, можно легко и с большой S °-ью получить с помощью опе-

стик с помощью фильтра, схема рационного усилителя И двух одина.. (которого да(на на рис. 4.5-3 ковых резисторов в цепи обратной

I I

связи. Для такого значения коэффициента усиления и функции Баттерворта третьего порядка получаем номинальные сопротивления резисторов: i?i = 1,565, 7?2 = 1,469, ?з = 0,435 Ом. Легко показать, что для К, равного двум, существует такое решение, которое дает положительное значение номинальных сопротивлений резисторов для любого выбора коэффициентов в (6) и для которого полином в знаменателе .функции цепи является полиномом Гурвица [37]. В табл. 4.5-1 приведена необходимая справочная информация для расчета каскадных реализаций нормированных фильтров Баттерворта различного порядка. Для заданного порядка п каждое значение в таблице дает номинальное сопротивление резистора для схемы второго порядка, показанной на рис. 4.2-3 (если определяются только Ri и Ръ) или для схемы третьего порядка, показанной на рис. 4.5-3 (если определяются Ri, R2 и Rz). В таблице предполагается использование единичных емкостей и коэффициента усиления ИНУН, равного двум.

Таблица 4.5-t

Реализация /?С-фильтров Баттерворта, использующая каскадное соединение звеньев второго и третьего порядков на одном усилителе

В табл. 4.5-2 и 4.5-3 приведена аналогичная информация, но для реализации чебышевских фильтров.

Теперь можно рассмотреть использование /?С-звена еще более высокого порядка на одном усилителе. Однако в общем случае чувствительность таких звеньев становится существенно больше, чем для звеньев, имеющих более низкий порядок. Для примера рассмотрим фильтр четвертого порядка, реализованный на одном усилителе или на двух каскадно-соединенных звеньях второго порядка, схемы которых приведены на рис. 4.5-5. Если обе реализации используются для получения характеристики Баттерворта и все коэффициенты усиления изменены на 5% от их номиналь-

Таблица 4.5-2

Реализация /?С-фильтров Чебышева с амплитудой пульсаций 0,5 дБ, использующая каскадное соединение звеньев второго и третьего порядков на одном усилителе

Таблица 4.5-3

Реализация JC-фильтров Чебышева с пульсацией 1 дБ, использующая каскадное соединение звеньев второго и третьего порядков на одном усилителе

ных значений, то в результате получаем картину, показанную на рис. 4.5-6. Очевидно каскад звеньев второго порядка обеспечивает лучшие характеристики. С увеличением порядка фильтра, реализованного одним каскадом, может существенно увеличиться чувст'

о-с

~г

о-с

г

Рис. 4.5-5. Реализация функции цепи нижних частот четвертого поря.дка: а-с помощью фильтра четвертого порядка; б -двух фильтров второго по рядка

вительность реализации. Для примера на рис. 4.5-7 приведены кривые чувствительности модуля реализуемой функции по отношению к значению коэффициента усиления К всех усилителей в данной реализации для фильтров Баттерворта пятого, седьмого и девятого порядков. Чувствительность минимизирована включением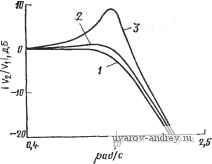

Рис. 4.5-6. Влияние 5%-ного изменения коэффициента усиления на АЧХ фильтра:

/ - АЧХ при номинальном значении коэффициента усиления; 2 - АЧХ яри 5%-ном изменении коэффициента усиления для каскадного соединения фильтров второго порядка; 3 -АЧХ при 5%-ном изменении коэффициента усиления для фильтра четвертого порадка

звена третьего порядка в каскадную реализацию комплексно-сопряженной пары полюсов с самой низкой добротностью. Чтобы показать, почему это важно, на рис. 4.5-8 приведен аналогичный график для фильтров девятого порядка, в которых фильтр третьего порядка реализует другую комплексно-сопряженную пару полюсов [38]. Очевидно, что для реализации звена третьего порядка в таком каскаде не следует выбирать высокодобротные пары.

С другой стороны, применяя методы каскадирования для реализации функций высокого порядка, следует отметить, что нет не-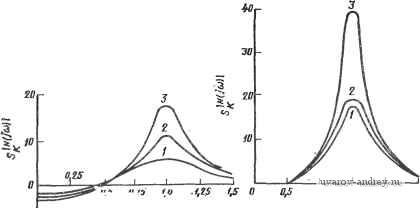

Т^З- 0,7S /,0

ц рад!с

Рис. 4.5-7. Чувствительность функции цепи к изменению коэффициента усиления каскадных реализаций с баттервортовской характеристикой:

.1 - пятый порядок; 2 - седьмой порядок; 3 - девятый порядок

0,75 1,0 1,tS GJ, padfc

Рис. 4.5-8. Чувствительность функции цепи к изменению коэффициента усиления для различных пар полюсов:

/ - с минимальной добротностью; 2 - с более высокой добротностью; 3 - с максимальной добротностью

обходимости использовать для реализации в целом звенья одного и того же типа. Например, если п четно и T{s) является полосовой функцией цепи высокого порядка, то один из вариантов состоит Б том, чтобы выбрать половину звеньев верхних частот, а половину звеньев нижних частот. Этот произвольно сделанный выбор нулей, связанных с определенным звеном, обеспечивает дополнительные преимущества. Есл'И отдельные передаточные функции имеют как комплексные нули, так и комплексные полюсы, то можно показать, что чувствительность i-ro звена можно уменьшить выбором подлежащих реализации нулей и полюсов настолько, насколько это возможно [39].

Другая важная особенность - выбор варианта, т. е. принятие решения, для каких полюсов и нулей должна быть реализована каждая каскадная реализация, иллюстрируется следующим примером.

Предположим, что необходимо реализовать полосовую функцию четвертого порядка, обладающую двумя комплексно-сопряженными парами полюсов и двумя нулями в начале координат (и двумя в бесконечности), как показано на рис. 4.5-9,а. Такую по-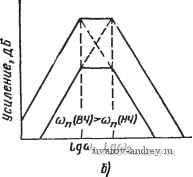

-JUf

Puc. 4.5-9. Каскадное соединение ФНЧ и ФВЧ

лосовую функцию можно реализовать в виде каскадного соединения звена нижних частот второго порядка и звена верхних частот второго порядка. Рассмотрим теперь, каково различие в выборе полюсов для этих звеньев. Сначала используем звено верхних частот для реализации лолюсов - oo±j щ и звено нижних частот для реализации полюсов - oo±j 0)2. Полученная в итоге диаграмма Боде показана на рис. 4.5-9,6 в виде кусочно-линейной зависимости, помеченной о)п(ВЧ) <о)п(НЧ). Если выбрать противоположную последовательность звеньев, то получим кривую, помеченную (Оп(ВЧ)>©п(НЧ). Хотя полюсы и нули передаточной функ-

ции в целом одинаковы в обоих слз^аях, коэффициент усиления в полосе пропускания будет выше для случая о)п(ВЧ) <:о)п(НЧ), чем для случая о)п(ВЧ) >(о„(НЧ). Причину легко понять, если проанализировать в отдельности каждое звено. В случае о)п (ВЧ) > >1соп,(НЧ) звено как верхних, так и нижних частот создает ослабление в полосе пропускания, тогда как в случае <й„(ВЧ)< <о)и(НЧ) ни одно из звеньев не вносит потерь в полосе пропускания; таким образом, для того чтобы достичь большого усиления предпочтительнее реализовать полюсы, расположенные наиболее близко к началу координат в звеньях верхних частот и полюсы, наиболее удаленные от начала координат в звеньях нижних частот. Более того, для достижения максимального динамического' диапазона необходимо ставить первыми звенья с минимальной добротностью. Это предохранит усилители от перегрузки. Другими-словами, даже если коэффициент усиления в целом окажется равным единице, отдельные высокодобротные звенья могут иметь достаточно высокий коэффициент усиления, так что сигнал может быть сначала усилен, а потом ослаблен последующими низкодобротными звеньями.

Пример 4.5-1. Полосовой фильтр высокого порядка. Требуется синтезировать ПФ, имеющий максимально плоскую АЧХ, используя каскадное соединение полосовых звеньев второго порядка. Средняя частота должна быть равна 3000 Гц с шириной полосы на уровне -3 дБ, равной 600 Гц, и шириной полосы на уровне -30 дБ не более, чем 1500 Гц. Коэффициент усиления IB полосе иропускания равен единице. Так как отношение ширины полосы на уровне -30 дБ к ширине на уровНе -3 дБ составляет 1500/600-2,5, можно прежде всего определить порядок нормированного ФНЧнпрототипа с шириной полосы на уровне -3 дБ, равной 1 рад/с, и минимальным затуханием 30 дБ на частоте 2,5 рад/с. Используя номограмму на рис. 2.1-4, находим, что порядок ФНЧ-прототипа должен быть равен четырем; это приводит к необходимости иметь четыре полосовых звена второго порядка для удовлетворения указанных условий. Табл. 2.1-3 дает нормированные значения полюсов ФНЧ-прототипа:

s .,2=0,3826 d=j 0,92388; s 3.4=0,92388±0,38268. (8а). (86)

Используя ФНЧ-ФВЧ-преобразование (см. § 2.4) и денормируя по частоте, получаем полюсы ПФ

Ри р*.=-1,67458-103±jl8,0616-103; (9а)

Р2, р*2=-1,80836-10=+jl9,5042-10=*; (96)

Рз, р*з=-0,65492-10=+jl7,1747-10=; (9в)-

Р4, р*4=-0,78775 10=±j20,6576-10=; (9г>.

0) f19588

в/= 13,21

-о

Рис. 4.5-10. Порядок каскадного соединения звеньев в примере 4.5-i

Используя приведенные выше значения корней, можно вычислить сощ и Qi для каждого из звеньев. В результате

ш„1 = 18139 рад/с, Qi = 5,416; (10а)

ш„2= 19588 рад/с, Q2=5,416; (106)

ш„з = 17187 рад/с, Q3=13,12I; (10в)

ш„4=20672 рад/с, Q4= 13,121; (Юг)

Порядок каскадного соединения звеньев показан на рис. 4.5-10. Предполагается, что коэффициент усиления на частоте резонанса каждого эвена равен единице.

4.6. Усилители с конечным коэффициентом усиления

В предыдущих параграфах этой главы мы познакомились со свойствами С-фильтров на усилителях. В этом параграфе рассмотрим свойства самого усилителя, в частности, влияние на характеристики усилителя с конечным коэффициентом усиления неидеальности операционного усилителя.

Общая схема неинвертирующего усилителя с конечным коэффициентом усиления дана на рис. 4.6-1. Для начала предположим, что операционный усилитель имеет бесконечно большое входное полное сопротивление и нулевое выходное полное сопротивление. Полагая, что A{s) коэффициент усиления схемы в целом, находим

А (S) = VoM/V, (s) = А, (s)/{l + А^ (S) [RM + s)]}- (1)

Используя для коэффициента усиления операционного усилителя с дифференциальным входом модель, учитывающую наличие одного доминирующего полюса, получаем

Лd(s) = G5/(s-fo)J = Лo}Дs-f o)J, (2)

где Ао-коэффициент усиления по постоянному току, Оа - ширина полосы, GB - произведение коэффициента усиления на ширину полосы, или ширина полосы единичного усиления. Подставляя (2) в (1), получаем

Л is) = Ко (s)/ys (s) = GB/{s + о)а [ 1 + Л, Ri/{Ri + R)]}

GB/[s + GBRM + 2)]. (3)

где приближенное выражение справедливо, если AoR\l{R\+R2)>-Тогда значение модуля и фазы (3)

IЛ (j £0) I = GB/ + [GBRM + R)f ; (4а)

arg [Л (j О))] = -arctg

{l+RM

(46)

Если ia<GB Ri/(R1+R2), то выражение (4) можно аппроксимировать следующими зависимостями:

Л (j (о)л^ 1 +R/Ri; arg [Л (j о)] -- (1 -R. (5а), (56)

Выражение (56) особенно важно для иллюстрации влияния частотной характеристики операционного усилителя на характеристики активного фильтра. Например, полагая, что l+/?2/-Ri = 3 и ro=G5/30, и используя (56), получаем, что такой усилитель с конечным усилением создает запаздывание фазы 5,73°. Это запаздывание может существенно влиять на характеристики реализации в. целом.

Рис. 4.6-1. Схема неинвертирующе-го усилителя с конечвым коэффициентом усиления

Рис. 4.6-2. Схема инвертирующего усилителя с конечным коэффициентом усиления

Общая структурная схема инвертирующего усилителя с конечным усилением приведена на рис. 4.6-2. Для нее передаточную функцию по напряжению

А (S) = Vo {s)lVs (s) =~А, is) [RARi + + Aa (s) [RJiRi + RS)-

Подстановка (2) в (6) приводит в результате к выражению Л (S) = Vo (s)/n;(s) = -IRARi + R}] GBl{s+oia [l+AoRJ(Ri + R2)]}f ir -IRARi + R)] GBl{s+GB [RAR1 + R2)]}, (7)

где приближенное выражение справедливо, если AaRi/{Ri+R2)>l. Амплитудно-частотную и фазовую характеристики (7) можно тогда выразить в виде

IЛ (/ ©) I = GBRARi + R2)/V+lGBRj{R+W; (8а) arg [А (j o))J = я-arctg [(mjGB) (1+RM]. (86).

Если (S)<GBRil{Ri+\R2), то выражение (8) можно аппроксимировать следующим образом:

\A(i(o)\RjRi (9а).

arg [А (jfo)] n~-{(o/GB) (1 -f R/R). (96)

Сравнивая (3) и (7), можно заметить, что полюсы инвертирующего и неинвертирующего усилителей с конечными коэффициентами усиления подобны друг другу. Существует, однако, одно отличие^ которое становится особенно заметным для низких значений коэффициентов усиления. Рассмотрим, например, усилитель с единичным коэффициентом усиления. Для неинвертирующей схемы-(см. рис. 4.6-1) требуется, чтобы Ri = oo и /?2 = 0. Следовательно^

полюс передаточной функции (3) расположен в точке s=- Для инвертирующей схемы, показанной на рис. 4.6-2, един ;- , ; усиление достигается при i?i=i?2- Из выражения (7) получаем vi&-полюс передаточной функции по напряжению этой схемы pT-tipff! ложен в точке s=-GB/2. Таким образом, инвертирующий усиД-тель с конечным коэффициентом усиления имеет более сущест]&2 йые частотные ограничения (ширина полосы вдвое уже), чем' инвертирующий усилитель. Очевидно, что, как только отношёШ. . R2(Rt становится большим, полюсы для обоих типов усилителями практически совпадают, принимая значение s=-GBRi/R2-

Рассмотрим теперь случай, когда входное и выходное полные сопротивления операционного усилителя неидеальны. В этой ситуации частотная зависимость величины Ad{s) приведет к тому, что входное и выходное полные сопротивления усилителя с конечным коэффициентом усиления также будут частотно-зависимы. Для этого случая [см. выражения (11) и (12) приложения Б] эквивалентные схемы усилителей показаны на рис. 4.6-3. В слу-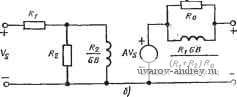

Рис. 4.6-3. Влияние входного и выходного соо'ротивлений операционного усиУ

лителя на параметры усилителей с конечным коэффициентом усиления: а - неинвертирующего; б - инвертирующего. Значения элементов даны воман.

генри, фарадах

чае неинвертирующего усилителя (см. рис. 4.6-За) A(s) опредес ляется выражением (3). В случае инвертирующего усилителя (см рис. 4.6-36). A{s) определяется выражением (7). При построении схем предполагалось, что R\ или R2 больше, чем Ro, и что R\ или R2 меньше, чем Ri. Другие подробности можно узнать, решая предложенные задачи. Точные эквивалентные схемы для этих усилителей можно найти в указанной статье :[40].

Для большинства применений активных фильтров значения входных и выходных полных сопротивлений усилителей с конеч-дым коэффициентом усиления практически не оказывают влияния на характеристики фильтра в целом. Как исключение можно привести реализации с отрицательным коэффициентом усиления, в которых входное сопротивление приблизительно равно R\, в результате чего нагружается /?С-цепь обратной связи. Другой проблемой в случае реализаций с отрицательным коэффициентом усиления является то, что отношение R2lR\ для схемы на рис. 4.6-2 должно быть велико для высокодобротных реализаций (для добротности, равной 10, /?2/J?i = 900). Однако из (86) следует, что для того, чтобы ограНичить запаздывание фазы, вызванное инвертирующим

\, лем, значением не более 6 при добротности 10, максималь- г' счетная инвертирующая частота должна быть порядка ). Так, если GB=l МГц, то указанное соотношение огра-чач : максимальную частоту фильтра приблизительно уровнем ). Эти и другие причины приводят к тому, что фильтры на глях с отрицательным коэффициентом усиления не пользу-опулярностью. Можно также сказать, что выходное полное со. явление неинвертирующих и инвертирующих усилителей с KOHvvibiM коэффициентом усиления мало влияет на характеристики активного фильтра в целом. Причина заключается в том, что эти сопротивления обычно малы, потому что внутренняя петля обратной связи, состоящая из резисторов Ri и R2, приводит к уменьшению собственного выходного сопротивления операционного усилителя.

Одним из параметров операционного усилителя, который оказывает заметное влияние на характеристики активного фильтра в целом, является скорость нарастания сигнала. Ограничения на скорость нарастания могут влиять на малосигнальные параметры усилителя с конечным коэффициентом усиления, когда уровень сигнала достаточно велик и/или частота сигнала достаточно высока. Чтобы убедиться в этом, рассмотрим модель влияния нарастания сигнала на характеристику усилителя, не охваченного обратной связью (см. приложение Б). Было показано [41], что если в схеме на рис. Б-12 вводится обратная связь [в этой схеме f{Vi) моделируется, как показано на рис. Б-13], то сигналы большой амш..1туды могут вызвать искажения как АЧХ, так и ФЧХ усилителя Для анализа таких искажений необходимо решить систему нелр ейных уравнений, поэтому здесь его проводить не будем. Однако важный результат такого анализа состоит в том, что для малого сигнала фазовый сдвиг инвертирующего усилителя можно запи ать в виде

arg [А (j О))] = я-arctg [(co/GB) (1 + R/R,)/N (Л)], (10)

где Л'(Л)-описывающая функция [42], а Л -амплитуда синусоидального напряжения, приложенного как Vi на рис. Б-12. Если искажения, вызванные конечной скоростью нарастания, отсутствуют, то Л^(Л) = 1. Однако, когда скорость нарастания влияет на рассмотренную характеристику, N{A) становится меньше единицы я приводит к возрастанию запаздывания фазы в режиме малого сигнала. Это, в свою очередь, может привести к возникновению проблемы обеспечения устойчивости для некоторых активных фильтров. Влияние искажений в режиме большого сигнала, описанное выше, показано графически на рис. 4.6-4 для инвертирующего усилителя с единичным коэффициентом усиления. Параметр

используемый на рисунке, предотавляет собой отношение {амплитуды входного сигнала) к пороговому уровню 6, определенному на рис. Б-13. На рисунке приведены как рассчитанные теоретически, так и наблюдаемые фактически значения. Если коэффициент усиления изменяется от -1 до -10, то в результате