Уз = 5Сз; 4=04 и У5==Уб = 0. Подставляя эти значения A3i(s), Ns2(s) и Nssis), определенные в (10), § 4.1, получаем, что передаточная функция (16) имеет вид

is) СгС^К

Vi (s) s2 C1C3 + s (GCg + G,Ci + GCs-KG + G G4 Деля числитель и знаменатель (19) на С1С3, получаехм

V2 is) sK

Уг (S) s+s{l/IiCi+l/RiCs+l/RiCi-KiR2Ci)+l/RRi С^Сд, Сравнивая полученное с (16), имеем

со = I/VR2R4C1C,; (21а>

(19) (20)

1 /Q = VRC,/RC1+VR2CJR Cs + VR2Cs/R Ci-K VRiCJR Cj

(216)

H-=K. (2lB)

Следуя первому варианту процедуры для цепи ФНЧ, § 4.2, и выбирая R2=Ri=R и Сх = Съ=С, получаем вариант /

r,-\lRC; l/Q3-K; Но = К, (22а), (226), (22в;)

который идентичен (14), § 4.2. Таким образом, ФВЧ-реализацию с добротностью Q = 0,7071 и Шп = 6280 рад/с можно получить, используя в схеме на рис. 4.3-2 значения R, С и К из примера 4.2-1, соответственно 1/С, 1/R и К.

Как и ФНЧ-реализацию в § 4.2 с положительным коэффициентом усиления, реализацию ФВЧ второго порядка можно получить подстановкой К=1. Полагая m = Cz/Ci и n=RJR2 и подставляя Ci = C и R2=R, получаем вместо (20)

I т+1 , 1

2(s)Ai(s) = sV

(23)

RC п т mn(RC)

Сравнивая полученное с (16), находим еще один вариант расчетных формул (вариант 2):

anVVmnRC; l/Q = {m+l)/Vmn. (24)

Отсюда видно, что для любого заданного значения п минимум 1/Q достигается при т=1. Так как обычно желательно иметь минимум 1/Q для любого заданного п, то примем т=1. В этом случае (24) упрощается и принимает вид

io=l/V RC; Q = Vn/2. (25)

Пример 4.3-3. Фильтр верхних частот с единичным коэффициентом усиления (вариант 2). Пусть требуется, используя ИНУН с единичным коэффициентом усиления, реализовать передаточную функцию по напряжению вида

V2 (S) /Vi (s) = s/ (s + 0,179 S + 0.988), (26)

где комплексная частотная переменная нормируется с постоянной 10 рад/с. Добротность и сОп норм имеют те же самые значения, что и найденные в при-

мере 4.2-2, а именно: 5,553 и 0,994 ра.д/.с. Из (25) находим, что n=4Q= = 123,34 и i?C=l/(B l/ 0,09058. Денормируя, получаем i?C=0,09058-10-<. Если выбрать С=0,01 мкФ, то i?=i?2 = 905,8 Ом и 7?4=111,72 кОм.

В другом используемом на практике наборе номиналов элементов /?С-фильтра верхних частот на одном усилителе с положительным коэффициентом усиления, показанного на рис. 4.3-2, емкости обоих конденсаторов имеют равные номиналы, а коэффициент усиления ИНУН равен двум. Тогда нормированные значения Ci = = Сз=С и /С=2. Используя выражение (20), в этом случае находим

(Onl/CVRjRl; is>jQ = (llC){2lR-\lR). (27)

Эти уравнения можно решить относительно R2 и Ri аналогично тому, как это было сделано в примере 4.3 - 2.

Рассмотрим теперь некоторые вопросы чувствительности схемных реализаций ПФ и ФВЧ, приведенных в этом параграфе. Сравнивая знаменатель передаточной функции нижних частот по напряжению, приведенной в (И), § 4.2, со знаменателями полосовой функции и функции верхних частот, приведенных соответственно в (8) и (20) этого параграфа, легко показать, что во всех этих случаях тип разложения полинома, используемый для получения комплексно-сопряженных полюсов, один и тот же. Таким образом, корневой годограф для всех трех фильтров имеет обший' вид (см. рис. 4.2 - 2). Анализ чувствительности реализаций ФВЧ и ПФ как таковой, приводит к результатам, аналогичным тем, что указаны в табл. 4.2 - 1 для ФНЧ. Например, чувствительности (Лп по К равны нулю для всех трех типов фильтров. Другие подробности такого анализа приведены в задачах.

В этом и предыдущих параграфах были обсуждены структуры Саллена и Ки на усилителе с положительным' коэффициентом усиления для ФНЧ, ПФ и ФВЧ. Преимущество этих структур заключается в том, что они характеризуются в общем случае простыми расчетными соотношениями; проектировщик имеет возможность легко управлять значениями номиналов элементов и их разбросом; кроме того, допустимо использовать небольшие значения коэффициента усиления ИНУН, которые удобны тем, что их легко стабилизировать. Есть также и некоторые недостатки; основной из них состоит в том, что они характеризуются высокими значениями чувствительности, если с их помощью пытаются реализовать схемы с высоким Q. Этот результат можно получить, не только анализируя чувствительность, приведенную, например, в табл. 4.2-1, но также исследуя форму их корневого годографа, показанного на рис. 4.2 - 2. Из рисунка видно, что когда полюсы высокодобротные, т. е. расположены близко к оси jco, небольшие изменения коэффициента усиления могут сдвинуть их в правую полуплоскость плоскости комплексной частоты и сделать, таким образом, цепь Неустойчивой. Одно из решений проблемы чувствительности, которое можно предложить, состоит в использовании структур фильт-

ров с отрицательным коэффициентом усиления усилителя, т. е. в использовании инвертирующих схем ИНУН. Корневой годограф таких фильтров не переходит в правую полуплоскость. Важно не только то, что эти фильтры всегда устойчивы, но и то, что чувствительность этих фильтров обычно ниже, чем чувствительность фильтров с положительным коэффициентом усиления. К сожалению, фильтры с отрицательным коэффициентом усиления имеют и некоторые недостатки: разброс номиналов элементов зачастую велик; методы проектирования их более сложны, и они требуют большого значения коэффициента усиления ИНУН, который труднее стабилизировать, чем небольшой коэффициент усиления. Однако в общем случае указанные недостатки перевешивают их достоинства. В результате фильтры с отрицательным коэффициентом усиления не используются столь широко. Некоторые примеры таких фильтров можно найти в задачах.

4.4. Фильтры, реализующие комплексно-сопряженные нули

В этом параграфе рассмотрим реализации активных фильтров для обобщенной передаточной функции второго порядка. Такие функции включают как частный случай ФНЧ, ФВЧ и ПФ. Их обычно относят к биквадратным функциям фильтрации. Общий вид биквадратных передаточных функций по напряжению второго порядка таков:

Vi (s) s+as + ao + (cop/Qp) s+mp

где H - постоянная, <0z и - нули и полюсы, соответствующие собственным частотам, а Qz и Qp - добротности комплексных нулей и полюсов. Предполагается, что нули могут быть вещественными или комплексными и что они могут быть расположены в любом месте на плоскости комплексной частоты, включая и правую полуплоскость. Выражение (1) может соответствовать и эллиптическим функциям, определенным в § 2.3. В этом случае оно принимает вид

Y = H + 0 =я + (2)

Fi (S) S2 + S -f flo s2 + (cop/Qp) s+

где нули расположены на оси jco.

Первый тип биквадратного фильтра, который мы рассмотрим, реализует (2) на основе схемы с одним усилителем и конечным коэффициентом усиления [28, 29]. Эта схема показана на рис. 4.4-1. Она соответствует общей схеме на рис. 4.1-3 и имеет функцию цепи, аналогичную (5), § 4.1. Из анализа этой функции

Формаль'н-о Q определяется только для комплексных полюсов; однако здесь удобно .распростраиить это понятие на нули.

видно, что нули 1/31 (s) определяют нули передаточной функции. Так как yzi представляет собой передаточную полную проводимость 7?С-цепи, то ее нули могут лежать на оси j(o, как это и требуется. Цепь, необходимая для реализации этой функции, является модификацией двойной Т-образной цепи [30]. Модификация со-

Рис. 4.4-1. Реализация биквадратной функции цепи на усилителе с конечным коэффициентом усиления. Значения элементов даны в омах.

а{тп+1)

стоит в добавлении одного резистора или конденсатора в качестве элемента У(s) на рис. 4.4-1. Если Y=IIR, то схема реализует (2) с ограничением ao>feo, означающим, что нули расположены ближе к началу координат, чем полюсы, в плоскости комплексной переменной. Передаточная функция с учетом этого ограничения имеет вид (случай 1)

V2 (S) Kjs+l/a} .3

Vi(s) s + l(m+l)/a]ll/R+{2-K)/m]s+l\ + {m+\)/R]/a

где а, т и К показаны на рис. 4.4-1 и где т можно выбрать произвольно, чтобы иметь возможность управлять разбросом номиналов элементов. Приравнивая (2) и (3), получаем расчетные соотношения:

а - УЩ; R{m+ 1)/(Со/&о-1): (4а), (46)

К = 2 + [m/(m + 1)] (С0/&0- l-ajVbo); Н^К. (4в), (4г)

Если y=aCs, то схема 4.4-1 реализует (2) с ограничением feo>Go, означающим, что теперь полюсы будут находиться ближе к началу координат, чем нули. Передаточная функция с учетом этих ограничений примет вид (случай 2)

(s) {K/[(m-bl)C-bl]}(s-bl/o)

ri(s) s-+s{[,m+\)[C+(2~K)lm]la[{m+\)C+\]}+\la[{m+\)C+\]

Приравнивая (2) и (5), получаем следующие расчетные соот ношения:

а-иУТо; C = {bJao-mm + l); (6а). (66)

/С = 2-t-[т/{т+1)] (&о/ао- KVoo); = (Оо/оЖ. (6в), (6г),

Как и раньше, множитель т можно выбрать произвольно.

Пример 4.4-1. Эллиптический фильтр нижних частот. Требуется реали.-зовать эллиптическую передаточную функцию по напряжению

У2(я)/У1(8) = (s2-J-7,464102)/(s2-l-0,998942s-i- 1,170077). (7).

В табл. 2.3-1 показано, что эта функция имеет амплитуду пульсаций-1 дБ в полосе пропускания и затухание не менее 17 дБ для всех частот, боль

ших чем 2 ра1д/с. Очевидно, применим случай 2; из выражения (6), используя т=0,2, найдем, что а=0,36603, С=4,4826, К=2.5078 я Я=0,39312. Полученная схема показана на рис. 4.4-2. Учитывая, что значение Я=0,139713 соответствует максимальному коэффициенту усиления в цолосе шрапуокаяия, равному единице (см. пример 2.4-2), получаем, что в данной реализации максимальный коэффициент усиления в полосе пропуокания равен 0,39312/0,139713= =.2,8138. ф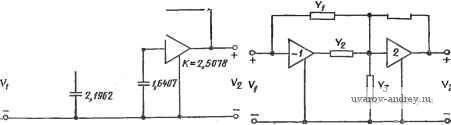

Рис. 4.4-2. Реализация эллиптического ФНЧ в примере 4.4-1. Значения элементов даны в омах, фарадах

Рис. 4.4-3. Реализация биквадратной функции цепи на двух усилителях с конечным коэффициентом усиления

Биквадратный фильтр второго типа, рассматриваемый в этом параграфе, представляет собой фильтр с двумя усилителями с конечным усилением. Одна из причин для рассмотрения такой структуры- сложность расчетных соотношений, полученных для схемы на одном усилителе, рассмотренной выше, когда нули передачи не расположены на оси jco. Структура фильтра с двумя усилителями С конечным усилением приведена на рис. 4.4-3 [31-33]. В этой реализации используется один инвертирующий усилитель с коэффициентом усиления, равным единице, и еще один неинвертирующий усилитель с коэффициентом усиления, равным двум. Оба они легко осуществляются с помощью операционного усилителя. Передаточная функция фильтра имеет вид

V, (.)/]/, (S) = 2 (Г1-П)/(Гз-П). (8)

Значения полных проводимостей можно найти путем деления числителя и знаменателя (1) на (s-bc), с>0, что делает возможным разложение на элементарные множители, реализуемые пассивными iC-цепями. Например, для числителя получаем

H(f + bs-\- bo)/{s + c) = Hs+Hb,/c + kt, s/{s + с) = 2 {Y,-Y,). (9)

Величина кь является вычетом полюса в точке s = -с;

kt, = Hic--cbi + bo)/{-c). (10)

Он может быть положительным или отрицательным, в зависимости от соотношения с, fei и feo- Если h - положительно, то ¥2= = 0 и

Fi (s) = Я s/2 -t- Я bo/2 с + \/{2/kb + 2 c/h s).

(11)

Реализация Yi в этом случае показана на рис. 4.4-4,а. Если же kb отрицательно, то

Y{s)=Hs/2 + Hbo/2c; Yis)=l/(2\kb\+2c/\kb\s). (12>

Их реализация приведена на рис. 4.4-4,6. Разложение на элементарные дроби знаменателя (1), деленного на (s+c), имеет вид

{ + 015 + ao)/(s +c)s+ Со/с -I- ka s/(s + с) = Fg- F4. (13>

Z ZC

2с Y?

\кь} Zc

с; 6)

Рис. 4.4-4. Реализация полных проводимостеи У\{в) и Y2{s) на рис. 4.4-3

Величина ka является вычетом соответствующего полюса в' точке s=-с;

К = (.с^-а,с-\-а,)1{-с). т

Если ka положительно, то 4=0 и

Fg (s) = S alc +1 /(I Ika + cfka s). (15>

Реализация показана на рис. 4.4-5,а. Если ka отрицательно, то

Fg(s) = s + ao/c; FJs)= l/(l/fej+c fejs). (16)

Их реализации приведены на рис. 4.4-5,6. Так как существует свобода выбора с, его можно выбрать так, чтобы либо ka или Ьь были равны нулю.

с

Рис. 4.4-5. Реализация полных проводимостеи Уз(5) н F4(s) на рис. 4.4-3

Пример 4.4-2. Всепропу екающая функция. Используя структуру на, рис. 4.4-3, реализовать следующую всепропускающую передаточную функцию:

V2{s)!VAs)=is-2s+l)/(s + 2s+l). . (17),

Если вйбрать с= + 1, то цепь упрощается. В этом случае получаем еле* дующее разложение на дроби:

(s2 2s + l)/(s + 1) = s + I -4s/(s + 1). (18)

Следовательно, Yi{s) = (s+l)/2 и y2(s)=2s/(s+l). Знаменатель разлагается следующим образам:

(s2-b2s-bl)/(s-bl)=s-bl. (19)

Таким образом, Уз(8)=5+1 и У4( )=0. Окончательный вид реализации показан на рис. 4.4-6. ф

Рис. 4.4-6. Реализация всепропуокаю-щего фильтра в примере 4.4-2. Значения элементов даны в омах, фарадах

Рис. 4.4-7. Реализация биквадратной функции цепи на усилителе с бесконечным коэффициентом усиления

Следует заметить, что схему, приведенную на рис. 4.4-3, можно также использовать для реализации функций цепи более высокого порядка. В этом случае числитель и знаменатель должны быть поделены на (s-fci) {S + C2) ... (s+Ch), где k меньше, чем степень числителя или знаменателя (любая из них больше).

Третий тип биквадратного фильтра реализуется одним усилителем с бесконечным коэффициентом усиления. Его схема показана на рис. 4.4-7 [34]; используется операционный усилитель с дифференциальным входом. Передаточную функцию такого фильтра легко найти

(s) Yi (F2 + Yb + Уз) -n (Yj + Ya + Г4) Vi (s) Уз(У1 + Ya+Y-y,(Уа + Yb + Уз)

Если У14-Уа + У4=У2+Уь + Уз или У„=У24-Уз или то (20) примет вид

Для упрощения синтеза любые общие множители (У14-У4) и (2+Уз) можно опустить. За исключением общего множителя 2, .выражения (8) и (21) в точности совпадают, таким образом, .процедура синтеза почти та же самая. Подробности оставляем получить читателю в качестве упражнения.

(20)

Уь = У.-1-У4. (21)

в четвертом типе реализации биквадратного фильтра, который рассматривается в этом параграфе, используются два операционных усилителя, как показано на рис. 4.4-8 [35]. Анализ этой схемы дает

У^тг (S) == {Уг- УМУь~ П). (22)

что совпадает с (21). Таким образом, к этой конфигурации также применима в общих чертах процедура синтеза фильтра, показанного на рис. 4.4-7.

Рис. 4.4-8. Реализация би-ивадратной функции цепи на двух усилителях с бесконечными коэффициентами усиления. Сопротивления даны в омах

Рассмотрим здесь еще одну реализацию биквадратного фильтра. Как видно из рис. 4.4-9,а, в ней используются двойные Т-образные цепи в качестве пассивных компонентов [36]. Передаточная функция фильтра по напряжению

УЛ) fs + (g/T)s + {b/n)

Vi(s) s+(ad/T)s + ll+a(2+b)]/T

где

(23)

b + 2g + e; f + 2 = d; T = RC. Из (1) и (23) получаем

(24)

(25)

ii>p=V\ + a{2 + b)lT; Qp = Y\+a{2-\-b)lad;

z = VfVTT; =Vbf/g; Яо = /.

Если Но, (Hp, (s)z, Qp и Qz подлежат определению, то приведенные уравнения можно разрешить относительно параметров а, Ь, е, i, g, R С. В табл. 4.4-1 показаны некоторые стандартные слу-

с

л/а

f

Лалосовая

9а

Рис. 4.4-9. Реалюация биквадратной функции цепи на усилителе с бесконечным коэффициентом усиления

чаи, в которых используются эти методы реализации фильтров второго порядка. Схема на рис. 4.4-9,а должна быть модифицирована, как показано на рис. 4.4-9,6, чтобы реализовать нули в правой полуплоскости. Если Ri=R3, то передаточная функция для схемы на рис. 4.4-9,6

Vo(s) р2 (2а/г)5-К1+2а)/7-

Ri U-b(2a/r)s+(I+2a)/H

В этом Случае получаются всепропускающие цепи. Процедура их синтеза приведена в последней строке табл. 4.4-1. Некоторые другие реализации биквадратных фильтров можно найти в § 5.2.

Таблица 4.4-/

Процедура синтеза фильтра на рис. 4.4-9

Всепропускающий

g+e = 2; g=4a

-R2 {s

2 a 1 -f 2a

f2a\ T2 j

/ 2a \2a\

4.5. Фильтры высоких порядков

Большинство методов синтеза, представленных в предыдущих параграфах этой главы, ограничивалось рассмотрением реализации фильтров второго порядка. Однако, как указывалось в § 4.1, такие реализации можно каскадировать для получения фильтров более высокого порядка, так как использование ИНУН в качестве выходного элемента обеспечивает необходимую изоляцию каскадов. Такое каскадное соединение будет иметь структуру, показан-

ную на рис. 4.5-1. Полная передаточная функция по напряжению T{s) будет определяться выражением вида

T{s)T(s)T,(s)...Tf,(s), (1)

где п - порядок фильтра в целом, причем он предполагается четным, а Ti{s) -передаточная функция по напряжению отдельного звена:

Ti (s) = {at s + (his+aoi)/ls + (w/QO s -f <.]. (2)

Существует ряд важных особенностей, которые нужно рассмотреть применительно к каскадным методам реализации функций более высокого порядка.

Рис. 4.5--1. Каскадная реали- вх зация, использующая звенья

второго порядка о-

вых

Рассмотрим сначала случай, когда функция, подлежащая реализации, имеет нечетный порядок. В этом случае существуют два возможных пути реализации. Первый из них состоит в том, чтобы добавить пассивное звено первого порядка, сделав его одним из элементов каскада. Это позволит реализовать отрицательный вещественный полюс, связанный с функцией нечетного порядка. В зависимости от того, должен или не должен реализовываться нуль в начале координат, пассивная цепь будет иметь вид, показанный либо на рис. 4.5-2,а, когда передаточная функция по напряжению (нуль в начале координат отсутствует)

(s)/Fi (s) = {llRC)]{s + IIRC), (3

либо на рис. 4.5-2,6, где передаточная функция по напряжению с нулем в начале координат)

V(s)lVAs)sl{s + llRC). (4)

Каждую такую схему удобно добавить как последний элемент каскада, в этом случае выход ИНУН предыдущего каскада обес-лечивает необходимую изоляцию. С другой стороны, пассивная

с

Рис. 4.5-2. Звено первого рядка

Рис. 4.5-3. Схема фильтра нижних частот третьего порядка Саллена и Ки