следующих параграфах используемая нами основная процедура будет распространена на другие типы функций цепи.

В общем виде передаточную функцию по напряжению ФНЧ второго порядка можно записать в виде

где Яо - коэффициент усиления на постоянном токе соп - собственная частота, а Q - добротность, определенная первоначально в § 3.5. Правая часть в формуле (1) взята из (П), § 4.1. Если полюсы функции цепи (1) располагаются в точках Рй = ооЛ-]ч>й, то между величинами сои и Q и положением полюсов имеется соотношение

Po = a ±jcOo=-±jV4Q-l. Это соотношение иллюстрируется рис. 4.2-1.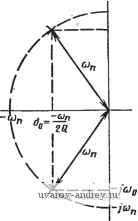

Рис. 4.2-2. Траектория изменения положения корней (4) в зависимости от изменения К

Рис. 4.2-/. Соотношевия между параметрами, определяющими комл-левсные полюсы

Сравним теперь (1) с соотношением, приведенным в (10), § 4.1. В первую очередь, обратим внимание на числитель; из (10а), § 4.1, следует, что коэффициенты а\ и Ог для ni{s) должны быть равны нулю. Таким образом, величины У] и Уз должны быть постоянными, т. е. должны представлять собой проводимости резисторов. Следовательно, их можно записать в виде

У 1 = 0; Уз=Сз. (3)

Рассмотрим теперь знаменатель выражения (1). Знаменатель правой части может рассматриваться как разложение полинома в знаменателе s-b (cu /Q)s + cu2 средней части этого выражения. Так как рассматриваются только функции второго порядка и так как Л/зз(5) и Л^з2( ) суть соответственно числители входной RC-

функции проводимости и передаточной проводимости лестничной Rf-mnn, то их положение нулей ограничено отрицательной ве-щ'ественной осью. Таким образом, если используется разложение-типа разность, см. (12), § 4, RC-cxeua на усилителе (рис. 4.1-4) формирует комплексно-сопряженные полюсы.

Как численный пример, основанный на (1), положим, что соп. нормирована к единице, Л^зз(5) =s + 3s-b 1 = (s-b0,382) (s+2,618) к N32(5) =s. Приравнивая знаменатели в (1), видим, что

s + (l/Q)s+l=(s + 0,382)(s-f 2,618)-7<:s. (4>

Корневой годограф этого выражения [полюсы функции цепи определены в (1)] изображен как функция коэффициента усиления ИНУН на рис. 4.2 - 2. Из рисунка видно, что как только К возрастает, полюсы (1) начинают двигаться из своих начальных точек s=-0,382; -2,618 (К=0) навстречу друг другу, совпадая в точке s =-1 (К=1). Затем они разбиваются на комплексно-сопряженную пару и, двигаясь по окружности, пересекают ось jco В: точке s=±jl (=3). Дальнейшее увеличение коэффициента усиления приводит к неустойчивости цепи.

Остальные элементы ?С-фильтра на усилителе можно определить, если обратить внимание, что в (10), § 4.1, требовалось выполнение условия Сг=70 (i = 0, 1, 2) для того, чтобы N33(3) была функцией второго порядка с вещественными отрицательными нулями. Кроме того, для того чтобы имелся простой нуль N32(5) в. начале координат, потребуем, чтобы 0 = 2 = О и ЬхфЬ. Используя эти результаты, получаем

iV32 = П (Gi + П + G3 + П) -f у 2 G3 = 61S; (5а>

Л^зз (S) = (Gs + П + П) (Сз + 2 -f Уь) +Сз (У4 + У,) = с, -Ь q S + Со-

(5б)<

При 0=2 = 0 видим, что из (5а) следует

Уа = S Са; Уе = О ; следовательно, N (s) = s Gg. (6)i

Очевидно, что при этом реализуется требуемый нуль в начале координат для N32{s). Используя этот результат, получаем вместо (56)

iV33 (S) = (G3 + У,) (Gi + S С, + У5) -f G3 У,. (7).

Для С2ФО потребуем, чтобы У^=8Сц. Подставляя это значение в (7), получаем

iV33 (S) = (G3 + S С4) (Gi + s -Ь У5) + SG3 Q. (8).

Теперь можно заметить, что подстановка У5 = 0 и полученное таким образом упрощение цепи позволяют удовлетворить требованиям СгФО. Сделав так, получим

Л^зз (S) = (Gg + S Q) (Gi + s Ca) + s Gg Q = CC+s (G3 Q + G Q +

+ G3Q) + G,G3. (9>

Окончательная реализация ?С-фильтра нижних частот на усилителе показана на рис. 4.2-3. Легко показать, что передаточная функция при этом будет иметь вид

V2 (S) GjGsK /10)

Fi (s) CC + s (Оз + Gi Q + G,Q -KG CnG.G,

Более привычная форма (10) достигается делением числитатя и знаменателя на С2С4 и использованием подстановки Ri=llGi. В результате

V2 (S) K/Ri С2 Q 1

Vi (s) s+s {l/Rs Q+I/i?, C, + l/R, C-K/Rs C4) + RgCC, Сравнивая (1) и (11), получаем следующий набор уравнении:

a>n=l/VRrRsC,C,- (12а)

1 /Q=VR3 cjRi С,+УЖс7Щск + (1 --Ю К^Гад^; (126)

Яо = 7. (12в)

Так как получаются пять неизвестных, а именно: Ru С2, R3, я К, к только три уравнения, то единственное решение можно получить, если положить, например,

Ri = R = R; С2 = С,=С. (13а),(13б) Подстановка (13) в (12) дает

w=l/RC; l/Q = 3-K; Но = К. (14)

Теперь легко получить набор расчетных формул (вариант /)

RCl/r; K = S-l/Q. (15)

В этом случае Яо не является больше свободным параметром, а ограничивается величиной К- Реализацию, показанную на рис. 4.2-3, часто называют активным RC-фильтром нижних частот Саллена и Ки}

ЧС=Ь

+ V2

Рис. 4.2-3. Схема фильтра нижних частот Саллена и Ки

Пример 4.2-1. Фильтр ниокних частот, имеющий одинаковые сопротивления и одинаковые емкости (вариант 1). Требуется синтезировать ФНЧ, для которого С0п=6283 рад/с (1 кГц) и Q=0,7071 (характеристика Баттерворта). Из (15) получаем

i?C= 1/6283 = 1,59-10-*; /С= 1,586.

(16)

См. работу Саллена и Ки [26], на которую чаще всего ссылаются специалисты то активным фильтрам.

I Если выбрать С=0,1 мкФ, то ii?=l,59 кОм. Окончательно получаем о= = 1,586. ♦

Другую процедуру синтеза (вариант 2) можно получить из (13), если примем /(=1. Используя выражение (12), получаем

1/Q = VRsCJRiC+УЖсЖС^. (17>

Определим теперь параметры

n-=Rs/Ri \ m = CjC. (18)

Следует заметить, что пит являются отношениями значений сопротивлений и емкостей соответственно. Далее положим

RR; С^ = С. (19)

Выражение (11) теперь можно записать как

V{s)/\\{s)il/mnRC)/[s + (l/RQ 1{п+ l)/n]s + l/mnRC]. (20)

Приравнивая (1) и (20), получаем следующие расчетные формулы:

сап=1/УШрС; 1/Q = (R+1)1/7. (21)

Из выражения для 1/Q можно получить, что для любого заданного значения т значение Q будет максимально, когда п=1. Однако этот случай не является оптимальным, так как, если п=1, то Q = 0,5l/m. Для более высоких. значений добротности требуется использовать существенно большие отношения емкостей. Более практичный подход состоит в том, чтобы выбрать значение т, совместимое со стандартными номиналами емкости конденсаторов так, чтобы

;n<l/4Q2. (22)

Тогда п можно вычислить из формулы

п = (1/2mQ~l)± {1/2mQ) VI-4mQ. (23)

Это выражение дает два значения п для любых заданных Q и т. Легко показать, что эти величины взаимно обратные; таким образом, использование любой из них дает тот же самый разброс значений элементов.

Пример 4.2-2. Фильтр нижних частот с единичным коэффициентом усиления (вариант 2). Пусть требуется использовать ИНУН с единичным коэффициентом усиления 1ДЛЯ реализации передаточной функции по напряжению-вида

Vs (s)/F, (s) = 0,988/(s2 + 0,179 s -f 0,988), (24>

ВДВ комплексная частотная переменная нормирована (ом. § 1.4) с коэффициентом 10-* рад/с. Из (1) получаем Юп ворм=0,994 рад/с и Q=5,553. В соответствии с (22) следует выбрать т<:0,0081. Принимая т=0,001, найдем из. (23), что п=0,0329 и 30,397. Если выбрать п=30,397, то из (21) с учетом того, что (в„=10(в„ норм, получаем J?C=5,7703 10-4. Если выбрать С2=С= =0,1 мкФ, то С4==100 яФ, J?i=K=5,77 кОм и i/?3=175,4 Ом. ф

(25)

Другой используемый на практике вариант активного ФНЧ на одном усилителе с положительным коэффициентом усиления зтолучается тогда, когда номиналы емкостей обоих конденсаторов одинаковы, а коэффициент усиления ИНУН принимается равным двум. Одинаковые номиналы конденсаторов удобны тем, что они могут быть нормированы по полному сопротивлению к стандартно применяемым на практике значениям. Коэффициент усиления 2,0 привлекателен тем, что можно получить его точное значение путем использования одинаковых по номиналу сопротивлений резисторов цепи обратной связи операционного усилителя. Из (1) и (11) для C2=Ci=C /С=2 легко найти (вариант 3)

Rs = l/Ri(о\ или i?3 = Пример 4.2-3. Фильтр нижних частот с равными номиналами емкостей м коэффициентом усиления, равным двум (вариант 3). Требуется реа.чизовать нормированную передаточную функцию по напряжению (характеристика Баттерворта)

Vs {s)/Vi (s) = 2/(s2 + T/fs + 1). (26)

для которой была проведена нормировка на 10. Из (25), используя С=1, >(о„=1 и Q=l/l/2, найдем Я,= 1/1/2~а J?8= Т/зГ Денормируя по частоте и -применяя дополнительное денормирование полного сопротивления с коэффи-циентом 10 получаем расчетные значения i?i=0,707 кОм, i?s= 1,414 кОм, С2=С4=0,1 мкФ и К=2. ф

Как было указано в связи с выражением (12), существуют только три основные характеристики функции цепи, а именно: Юп, Q и Яо, хотя существуют пять параметров цепи. Учитывая это, л{ожно сказать, что существуют, очевидно, другие процедуры синтеза, отличные от описанных выше, которые можно предложить для ФНЧ Саллена и Ки .[27]. В этом плане три процедуры, описанные в предыдущих параграфах, типичны для большинства из них. Другие процедуры можно встретить в задачах.

Теперь рассмотрим чувствительность фильтров Саллена и Ки. Для большей общности будем использовать цепь, показанную на рис. 4.2 - 4, в которой резисторы в цепи обратной связи операционного усилителя, определяющие коэффициент усиления, обозначены через Ra и Rb к где коэффициент усиления ИНУН К= 1 + +Rb/Ra- Используя определение чувствительности из § 3.5 и соот-шошения (12) и (1), получаем

Sl = -l/2 + QVRsCJR.C, -Si ; (27а)

= -1 /2 + Q(VR.CJRsC + VRTcTRTC) = -Sg,; (276)

-S% = QKV~r;QR,; S=-Q(K-mrR;CCi=-SRj, ;

(27b) , (27r)

Sl:.R,.c..c. = -1/2 ; в = О- (27Д), (27е)

Таблица 4.2-Г Чувствительности для трех вариантов ФНЧ Саллена и Ки

Значения полученных чувствительностей для вариантов /- приведены в табл. 4.2-1. Из таблицы ясно видно, что чувствительности Ши одинаковы для всех трех вариантов, тогда как чувствительности добротности изменяются в широком диапазоне.

Часто оказывается возможным снизить чувствительность, указанную в табл. 4.2-1, хотя при этом следует уточнить цену такого уменьшения. Чаще всего это приводит к увеличению разброса номиналов элементов. Например,

выбирая отношение 1:10 для сопротивлений резисторов i?i и /?з и 10:1 для емкостей конденсаторов Сг и С4, а не отношения 1:1, как было определено для варианта /, можно получить значительное уменьшение многих из рассмотренных чувствительностей. Аналогичные результаты получаются при выборе равными Ri и Кг для варианта 2. Наконец, значение коэффициента усиления можно выбрать так, чтобы получить наилучший компромисс между чувствительностями активных и пассивных элементов.

Примеры ряда описанных выше ситуаций можно найти в задачах.

Рис. 4.2-4. Схема фильтра нижних частот Саллена и Ки с использованием операционного усилителя

4.3. Полосовые фильтры и фильтры верхних частот на одном усилителе с положительным коэффициентом усиления

Б предыдущем параграфе использовалась общая конфигурация звена второго порядка на одном усилителе, описанная в начале этой главы и конкретизированная для схемы ФНЧ. В этой главе будем использовать аналогичные процедуры для того, чтобы получить схемы ФВЧ и ПФ. Рассмотрим сначала полосовую функцию цепи. Обобщенная полосовая передаточная функция по напряжению второго порядка имеет вид

2 (sWi (S) = Яо K/Q) s/ls + K/Q) S+ш2] == KN,i is)/[Ns (s) - KN,{s)].

В этом выражении Яо - максимальная амплитуда функции цепи в полосе пропускания. Эту величину часто называют коэффициентом усиления на резонансной частоте. Величины Шп и Q определяются точно так же, как они определялись для ФНЧ, а именно: (On - собственная частота^ и Q - добротность. Эти величины связаны с полюсами функции цепи так, как описано в (2), § 4.2, и на рис. 4.2-1. Правое выражение в (1) взято из (1Ц, § 4.1.

Сравнивая числитель (1) с (10а), § 4.1, видим, что коэффициенты йо и 2 должны быть равны нулю для /3i(s). Следовательно, проводимости Yi и Кз должны быть: одна емкость, другая - сопротивление. Пусть

n = G,; \\ = sC,. (2)

Следовательно, Ыз\{5) =sG\Cb. Используя ту же процедуру, что /была рассмотрена в связи с выводом выражений (5), § 4.2, получаем

ЛАз2 (S) = Y, (Gi+ + * Сз + П) + S Cg У^; (За)

ЛАзз {s) = (S Сз + У, + Уе) (Gi + У, -f У,) + s С3 (У, + Y). (36)

Разложение знаменателя может быть различным, имеющим те же формы, что и в случае ФНЧ. Чтобы получить его, выберем

52=2, Уе = О, следовательно, N. (s) = s Сд G. (4)

В этом случае

ЛАзз (S) = (S Сз + У,) (Gi + G, + П) + S Сз У4. (5)

Наконец, чтобы сделать N33(8) полиномом второго порядка, как это требуется при разложении, выберем Yi=Gi и Уб=5С5. В результате получим

ЛАзз (S) = Сз С5 -f S(Gi Сз -f Ga Сз + G, С3 -f G, Q) + G, (G-f G). (6)

* В оригинале как в § 4.2, так и в § 4.3 эти характеристики определя-.Ются ак недемпфированная собственная частота и коэффициент качества .-Ярыж. пер.

Передаточная функция по напряжению в целом примет вид

Kg (s) sKGCs

(s) s3 Сз Сб + s (Gi Cs + Q + G4 Cs + G4C5-/G,Cs)+G4(Gi + G) *

Ее можно записать также в виде

V2 (s) S fC/l

Vi (S) S2+S(l/7?1 Сб+1/?2 Сб+1/?4 C5+l/?4 Cs-KIR C)+(. ICsC) X

(8>

Полученная в результате схема показана на рис. 4.3-1. Ее обычно называют схемой полосового фильтра Саллена и Ки. Решая приведенное выше уравнение относительно параметров функции цепи в (1), получаем

(1 + RilRz) Ri i?4 Cs C5

[1 + (R1/R2) (1 -Ю] V Ri CsIRi С, + -УЩСЦЪ + VRjCRCs

KjRi Сб

Сб + I/R2 с, + l/i?4 Сб -f l/ 4 C3-K/R2 Сб

Одна из процедур получения /?2

единственного решения для зна-

чений элементов цепи - выбрать одинаковые номиналы сопротивле- о-I [-

(9а> (96) (9в)

Рис. 4.3-1. Схема полосового фильтра Саллена и Ки

±1-

(10) (И)

НИИ всех резисторов и емкостей всех конденсаторов. Следовательно (вариант /),

1 = 2 = 4 = > = С5 = С.

В этом случае соотношения (9) принимают вид

(OnVmC; Q = >2/(4-/C); H, = Kl(fi-K).

Решая их относительно RC и К, получаем

RC = ; К = 4- V2/Q. (12>

Заметим, что для того, чтобы Л' было положительным, Q должно быть, больше чем 2/4.

Пример 4.3--1. Полосовой фильтр с одинаковыми номиналами сопротивлений резисторов и емкостей конденсаторов (вариант 1). Пусть требуется реализовать ПФ, у которого Q=10 и <0п=104 рад/с. Из (12) находим, чта RC=\/2-lO-* с и К=3,8586. Выбирая С=0,1 мкф, получаем iJ?= 1,414 кОм.. В результате Яс=27,289. ф

Существует много возможностей выбора значений элементов фильтра, показанного на рис. 4.3-1, отличающихся от тех, что приняты в (12). Другой практический вариант синтеза состоит в шыборе коэффициента усиления ИНУН, равного двум, который, как уже было указано, легко получить с большой точностью, ис-яюльзуя два одинаковых высокоточных резистора в цепи обратной связи операционного усилителя. В этом случае можно выбрать следующие соотношения между номиналами (вариант 2):

/?1 = Сз = С5 = 1, К=2. (13)

При таком выборе номиналов, приравнивая (1) и (8), получа-

ш^ = (l + l/;?2)/,; a) /Q=l+2 ?,-l ?2. (Иа), (146)

Эта совместная система нелинейных уравнений легко решается, позволяя получить определенные значения Ши и Q.

Пример 4.3-2. Полосовой фильтр с равными номиналами емкостей и коэффициентом усиления усилить чя, равным двум (вариант 2). Пусть тре-буется синтезировать ПФ, нормированный по частоте и полному сопротивлению, (ДЛЯ которого (Вп = 1 -и Q=2. Ыоминалы емкостей конденсаторов при этом .должны быть равны единице, а коэффициент усиления ИНУН - двум. Используя (14) н полагая для удобства dllRu получаем

[1 = (1-С2)С^; 0,5 = 1+204-02. (15а), (156)

Решая первое уравнение относительно О4, подставляя результат во вто-.рое уравнение и приводя подобные члены, получаем 02+0,502-2,5=0. Решая это уравнение относительно О2 и подставляя результат в (15а), находим, что i?2=0,7403 Ом i?4=2,3508 Ом. ф

Различные схемы ПФ, основанные на схеме, описанной выше, получаются путем подстанов'ки Vi = sCi и Уз = Сз вместо того, чтобы использовать соотношения (2). Осуществляя далее указанную процедуру реализации, приходим к схеме с тремя конденсаторами. Как таковая она представляет меньший практический интерес, чем схема, описанная выше. Другие подробности, относящиеся к этой схеме, можно найти в задачах.

Второй тип фильтров, который рассматривается в этом параграфе, - ФВЧ. Обобщенная передаточная функция по напряжению ФВЧ второго порядка имеет вид

(s) Яр 5 KNsi (S)

Viis) s2 + ((B /Q)s + Nss{s)-KN32{s)

В этом выражении Яо - коэффициент передачи на бесконечно большой частоте, а со , Q и член в правой части (16) определяются аналогично тому, как в (1). Схему фильтра, реализующ ,ю эту функцию цепи, можно получить аналогично тому, как были получены полосовая функция и функция цепи верхних частот. В данном случае выберем более простой путь. Заметим, прежде всего, что этот тип функции цепи легко получить из функции нижних частот, если воспользоваться ФНЧ-ФВЧ-преобразованием, вне-

денным в § 2.4, а именно: положить s=l/p, где s - исходная переменная комплексной частоты ФНЧ-прототипа, ар - новая комплексная частотная переменная ФВЧ.

Теперь можно непосредственно использовать ФНЧ-реализацию для получения ФВЧ-реализации путем применения указанного преобразования частоты к элементам исходной схемы. Кроме того, можно применить нормирование полного сопротивления Это

последнее преобразование не нарушит инвариантности передаточной функции по напряжению, учитывая ее безразмерную величину. Для любого резистора (ФНЧ) с сопротивлением R рассмотренная процедура сводится к следующему:

ФНЧ - ФНЧ-преобразование

.пРеобр(Р)-/Р- (17)

Нормирование полного сопротивления 1/р

Результатом этих двух преобразований будет, очевидно, емкость, равная \/R, в реализации ФВЧ. Аналогично для емкости (ФНЧ) С получим

Yn4{s) = tC

Fb4(s) = C/p

Yz up еобр (P) - С.

ФНЧ - ФНЧ-преобразование Нормирование полного

сопротивления 1/р

Таким образом, в этом случае результатом двух указанных преобразований будет сопротивление, равное 1/С Ом. Так как коэффициент усиления ИНУН безразмерен и независим от частоты, ИНУН остается инвариантным после этих преобразований. Полученные результаты сведены в

Таблица 4.3-1

Преобразование элементов цепи при переходе от ФНЧ к ФВЧ

1. Используя данные применительно

C=t/R

табл. 4.3 этой таблицы

к цепи на рис. 4.2-3, получим реализацию ФВЧ, показанную на рис. 4.3-2. Таким образом, получаем следующие соответствия для пассивных элементов на рис. 4.1-4: F, = sCi; Y2 = G2\

R=i/C

o--o-J-о

I--o I-о

о--о

Рис. 4.3-2. Схема фильтра верхних частот Саллена н Ки