Типичные характеристики конденсаторов, пригодных для использования в активных фильтрах

ся слюдяные, полистироловые, полипропиленовые и керамические (типа NPO) конденсаторы.

Результаты и выводы, полученные при изучении различных типов чувствительностей, рассмотренных в этой главе, окажутся полезными в последующих главах. В общем случае меры чувствительности дают одну из наиболее важных методик оценки раз-.личных типов активных и пассивных реализаций фильтров, следовательно, мы еще не раз сошлемся на материал по чувствитель-iHOCTH в оставшихся главах этой книги.

3-1 (§ 3.1). а) Выведите: а) свойство (7) в табл. 3.1-1; б) свойство 14; т) свойство 15.

3-2 (§ 3.1). Покажите, что производная функции чувствительности Sx для случая, -когда у является фунвдией х (причем яе обязательно линейной) определяется 1как [23]:

3-3 (§ 3.2). а) Начертите графики, аналогичные тем, что были приведены на рис. 3.2-2, для случая, ковда индуктивность L в примере 3.2-1 яв-.яяется варшруемым параметром.

б) Повторите то же для случая емкости С.

3-4 (§ 3.2). а) Найдите чувствительность для цепи, показанной

а рис. 3.3-4, где N(s)-передаточная функция по напряжению разомкнутой щепп V2{s)IVi{s) ах - индуктивность i.

б) Повторите то же для емкости С.

в) Повторите то же для сопротивления R.

г) Повторите то же для активной проводимости G.

Рис. 3. 3-4. Значения элементов схемы даны в омах, снм.менсах, генри, фарадах

3-5 (§ 3.2). Покажите, что соотношения (15) в § 3.2 для цепи, иополь-.зуемой в примере 3.2-1, согласуются с графика'ми, приведенными на рис. 3.2-2.

3-6 (§ 3.2). Найдите миогопараметрические вариации rfAf(jl)/JV(jl) для >фуикции цепи, описанной в задаче 3-4, относительно параметров L, С, G 4i R

3-7 (§ 3.3). а) Найдите чувствительность коэффициентов для функции а1,епи N{s), определенной в задаче 3-4, по отношению к индуктивности L. б) Повторите то же для емкости С. в) Повторите то же для сопротивления Л. т) Повторите то же для активной проводимости G.

3-8 (§ 3.3). а) Используя результаты задачи 3-7, получите чувствительности для N(s) по отношению к индуктивности L, полученной в задаче 3-4. б) Повторите то же для емкости С.

в) Повторите то же fljyi сопротивления R.

г) Повторите то же для активной проводимости G.

3-9 (§ 3.3). Используя чувствительность коэффициентов, определенную в (6), § 3.3, найдите чувствительность функции цепи относительно К для цепи на рис. 3.3-1. Проверьте правильность результата путем непосредственного вычисления чувствительности.

3-10 (§ 3.4). Подтвердите правильность соотношений (8) в § 3.4.

3-И (§ 3.4). Найдите ненормированную чувствительность полюсов цепи в примере 3.2-1 относительно параметров R, L и С.

3-12 (§ 3.4). а) Докажите, что траектория полюсов для функции цепи в примере 3.2-1 по отношению к вариации сопротивления R представляет собой окружность.

б) Повторите то же для индуктивности L.

в) Повторите то же для емкости С и покажите, что траектории полюсов - Гфямые линии.

3-13 (§ 3.4). а) Найдите ненормированную чувствительность полюсов для функции цепи iV(s), определенной в задаче 3-4, относительно индуктивности L.

б) Повторите то же для ем:кости С.

в) Потвторите то же для сопротивления R.

т) Повторите то же для активяой проводимости G.

3-14 (§ 3.4). Используя чувствительность коэффициентов, приведенную в табл. 3.3-1, найдите ненормированную чувствительность полюсов цепи в примере 3.2-1 относительно inaipaMCTpoB R, L п С. Сравните результаты с теми, что были получены в задаче 3-11.

3-15 (§ 3.4). Используя чувствительность коэффициентов, определенную в задаче 3-7, найдите ненормированную чувствительность полюсов для цепи рис. 3.3-4 относительно параметров L, С, \R и G. Сравните результаты с теми, что были получены в задаче 3-13.

3-16 (§ 3.4). Используя чувствительности коэффициентов, определенные в (6), § 3.3, найдите ненормированиую чувствительность полюса относительно К для цепи на рис. 3.3-1. Сравните результаты с выражением (8) в § 3.4.

3-17 (§ 3.4). Для цепи на рис. 3.2-1 примите следующие значения элементов: £=1, С=1, \R=2. Используя технику обращения с кратными полюсами, представленную в § 3, 4, определите изменения в положении полюсов при изменении \R nz +1%.

б) Повторите то же для изменения R на -1%.

3-18 (§ 3.4). Повторите задачу 3-17, используя в качестве варьируемого параметра С.

3-19 (§ 3.4). Повторите задачу 3-17, используя в качестве варьируемого параметра L.

3-20 (§ 3.4). Выведите чувствительности функции цепи, приведенные в примере 3.2-1, основываясь на ненормированных значениях чувствительности полюсов, найденных в задаче 3-11.

3-21 (§ 3.5). Найдите чувствительности Q и сОп для цепи, описанной в примере 3.2-1, по отношению к элементам R, L к С.

3-22 (§ 3.5). а) Найдите чувствительности Q и сй для цепи, описанной в даче 3-4, относительно индуктивности L. \ б) Повторите то же относительно емкости С. ! в) Повторите то же относительно еапротивления R. \ г) Повторите то же относительно активной проводимости G. \ 3-23 (§ 3.5). Схема цепи нижних частот, третьего порядка, показанная на рис. 3.5-1, имеет функцию цепи, определенную в примере 3.5-2, и используется для реализации чебышевской характеристики третьего порядка с пульсацией 0,5 дБ. Требуемые значения элементов К=2, i?i=0,268I Ом, Rz= =2,778 Ом, i?3=ij,876 Ом, а все емкости равны единице [24]. Найдите чувствительности Q и со и по отношению к К.

3-24 (§ 3.6). а) Найдите статистическую мнoгoпapaмeтpиqвcкyю чувствительность в диапазоне частот О ... I рэд/с для передаточной функции по напряжению цепи, показанной на рис. 3.3-24. Рассмотрите только знаменатель и предположите, что нормированные рвариации значений элементов некоррелнро-ваны и имеют равномерное распределение с дисперсией IQ-.

б) Повторите то же, но для случая, жогда коэффициент корреляции между элементами равен -0,7.

Рис. 3.3-24 Рис. 3.3-25

3-25 (§ 3.6). а) Найдите статистическую многопарамечрическую чувствительность в диапазоне 1частот О ... I рад/с для передаточной функции по напряжению цепи, показанной на рис. 3.3-25. Рассмотрите только знаменатель и предположите, что нормированные вариации элементов некоррелированы и имеют равномерное распределение с дисперсией 10.

б) Повторите то же для случая, когда коэффициент корреляции между всеми элементами равен -0,7.

3-26 (§ 3.7). Убедитесь в спра1ведл1иеости анализа во временной области для токов 1В ветвях и напряжений, цриведенных в примере 3.7-1.

3-27 (§ 3.7). Используя метод присоединенных цепей, найдите чувствительность У(]1й) к параметрам R, L к С для цепи, определенной в примере 3.2-1. -sss*

3-28 ( § 3.7). Найдите чувствительность передаточной полной проводимости для цепи, схема которой показана иа рис. 3.7-4 к изменению элементов схемы. Передаточная полная проводимость выражается в виде 121=-/рг/Урь где пара зажимов 2 определяется как пара зажимов в правой части цепи, полученная путем удаления вертикальной черты, показывающей короткое замыкание схемы.

3-29 (§ 3.7). Подтвердите яравильность определе.чия чувствительностей, найденных в примере S.7-2, толучив выражение для /?вх и взяв соответству-гощие частные производные.

С.фИЛЬТРЫ НА УСИЛИТЕЛЯХ. ЧАСТЬ 1

.Эта и следующие главы посвящены общим вопросам активных фильтров. Если говорить более конкретно, в них рассмотрены методы реализации всех типов функций цепи, основанные на использовании схем фильтров, включающих как активные, так и пассивные .элементы; из последних будут рассматриваться исключительно резисторы и конденсаторы. Такие фильтры относят к классу активных RC-фильтров или безындуктивных фильтров. Использование активных фильтров привлекательно по целому ряду причин и может быть предпочтительней пассивных iLC-экви-валентов. Например, активные iC-фильтры обычно имеют меньшую массу и занимают меньше места, чем пассивные. Это имеет большое значение при использовании фильтров в аэрокосмических приборах. Другое преимущество - активные фильтры могут быть изготовлены в микромодульном исполнении при использова-шш технологии интегральных микросхем. Кроме того, они относительно недороги и могут производиться в массовол масштабе. С другой стороны, так как катушка индуктивности не может быть выполнена в интегральном исполнении, то пассивные схемы можно создать только с помощью дискретных компонентов. Этот вариант значительно дороже. По .этим и ряду других причин во многих традиционных областях применения фильтров, особенно в радиосвязи, приходится проводить модернизацию, направленную на исключительное использование активных фильтров. В результате .этого ежегодное производство активных фильтров юценивается миллионами, и многие компании предлагают их как стандартные блоки. В этой главе познакомимся с одним из наиболее широко используемых типов активных /?С-фильтров - RC-фильтрами на усилителях.

4.1. С-фильтры на усилителях

Существуют два общих метода использования активных RC-фильтров при реализации функции цепи. Первый из них - метод каскадной реализации. Этот метод называется так потому, что реализуем.ая функция сначала факторизуется (разлагается на

\произведение сомножителей второго порядка). Каждый сомно китель реализуется затем отдельно активной 7?С-схемой, после -его каскадируется, или последовательно соединяется с другими, обы реализовать функцию цепи в целом. Отдельные активные 7?1С-схемы, конечно, должны быть синтезированы так, чтобы он не взаимодействовали друг с другом.

Второй общий метод использования RC-схем для реализации фуккций цепей - метод непосредственной реализации, в котором для реализации функции в целом используется одна единственная, схема. Этот метод обсуждается в гл. 6.

1аскадный метод использования активных RC-cxeu для реализации функций цепи дает много преимуществ инженеру-проек-тиро,вщику. Прежде всего, любая рассматриваемая JC-схема, требуемая для реализации звена второго порядка обычно относи--тельно проста, а число требуемых элементов невелико. В результате этого процедура синтеза, необходимая для определения значений элементов, обычно несложна и позволяет легко учесть дополнительные ограничения, такие как использование стандартных номиналов элементов или ограничения, накладываемые при* минимизации чувствительности. Другое преимущество состоит bi том, что каждое звено второго порядка можно индивидуально настроить для реализации соответствующей характеристики. ЭтOi, конечно, значительно легче, чем пытаться настроить схему, в которой все элементы взаимодействуют друг с другом; именно это и происходит, когда используется непосредственный метод реализации.

Рассмотрим теперь активный элемент активного ?С-фильтра'. Хотя теоретически в качестве такого активного, элемента м'ожно использовать любой тип управляемого источника, на практике чаще всего используется один ИНУН (источник напряжения, управляемый напряжением). Идеально ИНУН представляет собой четырехполюсник, который характеризуется следующими свойствами: 1) бесконечно большим входным полным сопротивлением-2) нулевым выходным полным сопротивлением; 3) выходным напряжением, пропорциональным входному, причем коэффициент пропорциональности обычно называют коэффициентом усиления. Эквивалентная схема и вариант обозначения схемы приведены на рис. 4.1-1. Часто ИНУН называют просто усилителем напряже-

Рис. 4.1-1. Схематическое изображение источника напряжения, управляемого напряжением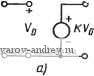

I--1

-о

* Если реализуется функция нечетного порядка, то необходимо использовать в каокадном соединении либо паооивное звено первош порядка, либо активное звено третьего порядка. Подробнее ом. в § 4.5. .

ния или, еще проще, усилителем. Коэффициент усиления можр,!;,. быть положительным (в этом случае говорят, что ИНУНд.и11:/:К вертирующий) или отрицательный (в этом случае говор:> .п,/!., он инвертирующий). Среди других причин широкого pacn,j-.,-j..i-нения ИНУН как активного элемента активных ?C-фй;:vтpc>в можно указать на легкость его реализации с помощью операционного усилителя. Например, неинвертирующий ИНУН можно реализовать, используя операционный усилитель с дифференци-альным входом; схема реализации показана на рис. 4.1-2,а. jKo-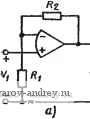

-о о-1-о о * о

6) в

Рис. 4.1-2. Реализация ИНУН: а - неиввертирующая; б - ловторитель напряжения; в - инвертирующая

эффициент усиления полученного ИНУН определяется соотношением

VjVi = {R. + Rx)IRx-=K. (1)

Очевидно, что коэффициент усиления всегда больше единицы. Неинвертирующий ИНУН с единичным коэффициентом усиления можно реализовать так, как показано на рис. 4.1-2,6. Эту схему называют обычно схемой повторителя напряжения. Инвертирующий ИНУН можно реализовать так, как показано на рис. 4.1-2,в. Его коэффициент усиления

VJV-RlRiK. (2)

Теперь можно определить конфигурацию обобщенного активного С-фильтра, который состоит из пассивной шестиполюсной С-цепи и соединенного с ней ИНУН (рис. 4.1-3). Эта схема и будет в дальнейшем называться RC-фильтром на усилителе. Основной функцией цепи для такой схемы является передаточная

функция по напряжению

о

Пассивная цепь

V2{,s)IVi{s). Заметим, что благо- даря нулевому выходному полно-о му сопротивлению ИНУН функ-+ ция цепи, реализуемая этим филь-Vz тром, полностью независима от - любой другой цепи, присоединенной к выходным зажимам, на ко-Рис. 4.1-3. Структурная схема RC- Рых определяется напряжение фильтра с одним усилителем V2(s). Таким образом, операцион-

Х й усилитель такого /?С-фильтра обеспечивает необходимую ;ю между каскадами, требуемую при каскадной реализа-

\ Уктуру ?С-фильтра на усилителе можно проанализировать, рассматривая, в первую очерезь, пассивную шестиполюсную цепь, которая определяется системой полных проводимостеи короткого замыкания или системой г/-параметров. Следовательно, для ука-зан^юй пассивной цепи на рис. 4.1-3 можно записать

где, учитывая пассивный характер цепи, yij{s)i=yji{s), т. е. у-мат-рица симметрична. Учитывая характерные особенности ИНУН, имеем

/з() = 0; V,{s) = K/s(s). (4)

Объединяя (3) и (4), получаем передаточную функцию по напряжению 7?С-фильтра на усилителе

V2 (s) i {s)-K Уз1 т Узз (S)+к г/з2 (S)]. (5)

в большинстве /?С-фильтров на усилителях, которые рассматриваются в этой главе, будем ограничивать пассивную цепь структурой, показанной в квадрате, обведенном штриховой линией на рис. 4.1-4. Чтобы найти /-параметры этой цепи, напишем, прежде-всего, уравнения узловых напряжений

h О

О

О

О

О

О

Уг + Уг + У^ + У, }

\\-

где для удобства убрали обозначение зависимости (s). Левые части третьего и четвертого уравнений принимаются равными нулю, так как внешние токи, приложенные к третьему и четверто-

ассивная I цепь

Рис. 4.1-4. Схема /?С-фильт.ра с одним усилителем и пассивной цепью специального шда

му узлам, отсутствуют. Если разрешить четвертое уравнение от* носительно Vi, то получим

П = + Y,V, + Уз V,yD (s),

где

D{s) = Yi + Y + Y, + Y,. Подставляя (7) в (6), найдем

(7) (8)

О

D(s) Y, F,

D(s)

D(s)

Y2Y3 D(s)

D(s) \r Y2 F3

D(s)

Y, + Y,+Y,-

При сравнении полученного с (3) видим, что эти соотношения определяют /-параметры пассивной цепи, показанной на рис. 4.1-4. Если теперь наложить ограничения и считать, что каждая из полных проводимостей будет либо активным сопротивлением, либо емкостью, то полиномы, которые будут стоять в числителе выражений, описывающих эти параметры, будут иметь, самое большее, второй порядок. Таким образом, для у-параметров, использованных в (5), можно написать

- Уз1 (S) = = = К s + a,s+a,)ID{s); (1 Оа)

- г/з2 (S) = [Y, (F,+Г, + Уз + П) + П YVD {s) - Л^з2 {s)lD (s) =

= {bs + biS + bo)ID{s); (106)

Узз (.) = (з + К, + Ке)(К, + К, + П)+Кз(П + Кв)

D(s)

= (c2S + qs + Co)/D(s). (10в)

Эти соотношения, которые определяют коэффициенты полиномов N?,\{s), Ns2{s), Nsz{s) в выражении (10), содержат только суммы и произведения проводимостей пассивных, т. е. имеющих положительные значения сопротивлений, резисторов и емкостей конденсаторов. Таким образом, коэффициенты этих полиномов могут быть только положительными (или равными нулю). Учитывая этот факт, можно переписать обобщенную передаточную функцию по напряжению (5) с учетом положительности этих коэффициентов полиномов:

V, {sWi {s)=KN,i {s)/[N {s)-KN (s)]. (11)

Из этого выражения видно, что если коэффициент усиления ИНУН положителен, т. е. если ИНУН неинвертирующий, то раз-

Ложение полинома знаменателя указанной передаточной функции шлет иметь вид разложения типа разность. В этом случае передаточная функция по напряжению в целом также будет неинверти-рующей. Аналогично, разложение типа сумма получим тогда, ког-да\ коэффициент усиления ИНУН будет отрицательным; в этом случае передаточная функция по напряжению также будет инвертирующей. Из практики известно, что использование неинверти-рующего ИНУН дает лучшие результаты. Причины этого будут указаны в следующем параграфе этой главы. Следовательно, разложение типа разность является более важным. Один из многих видоЬ такого разложения обычно встречается в ?С-фильтрах на усилителях. В этом случае полином второго порядка в знаменателе P{s) можно разложить так:

P(s) = s2 + a,s + ao {s+a){s+a)~Kas, (12)

где Oi и ао определяют результирующее положение полюсов, а Си 02 и а являются функциями различных пассивных элементов цепи. При таком разложении корневой годограф (как функция Л') имеет вид окружности (рис. 4.1-5). Из рисунка видно, что когда К, увеличиваясь, становится больше величины (01 + 02)/а, то полюсы функции цепи сдвигаются в правую полуплоскость и цепь становится неустойчивой. Для нормированного по частоте полинома знаменателя, имеющего вид P(s)=s+ {l/Q)s+l, оптимальным разложением типа разность будет разложение is+l)-Kas. р„,. 4.; 5. р,з„ е на разность Оно дает нижнюю границу оценки составляющих

для равную 2Q-1 [25]. Так

как эта величина относительно велика, ?С-реализации на усилителях пригодны в общем случае только для функций цепи с низкой добротностью.

4.2, Фильтры нижних частот на одном усилителе с конечным коэффициентом усиления

В предыдущем параграфе была представлена основная конфигурация ?С-фильтра на усилителе, пригодная для использования в реализациях передаточных функций по напряжению второго порядка. Схема была приведена на рис. 4.1 - 4. В этом параграфе покажем, как можно использовать общую структуру, показанную на этом рисунке, для реализации функций цепи нижних частот. В

Детальное исследование разложения типа суммы и разности можно най-га я 1[13].