состоит в использовании одной из многих существующих программ машинного проектирования, таких как ASTAP, SYSCAP, SCEPTRE или SPICE. С их помощью можно провести анализ цепи с номинальными значениями элементов, затем повторить анализ, изменив значение одного из элементов. В общем случае это не очень желательная процедура, так как она требует большого числа повторений такого анализа, по одному на каждый элемент. Кроме того, точность вычислений невысока, так как зависит от точности вычисления разности двух близких чисел. В этом параграфе представим значительно более эффективный метод.

В качестве предварительного шага при разработке эффективного метода вычисления чувствительности рассмотрим теорему Теллегена.

Пусть V - вектор напряжений ветвей данной цепи Л^, а Vm - вектор независимых узловых напряжений; из общих топологических соображений известно, что существует матрица инциденций А, которая в соответствии с законом Кирхгофа обладает тем свойством, что v=Av *. Кроме того, если предположить, что i- вектор токов ветвей, то в соответствии с законом токов Кирхгофа Ai = 0. Из этих соотношений получаем

iTv = v-i = (Av )4 = v;:;Ai = 0. (1)

Полученный результат говорит о том, что сумма мгновенных мвщностей, поступивших во все ветви данной цепи, равна нулю, т. е. что мощность сохраняется. Рассмотрим теперь второй четырехполюсник Й с вектором токов ветвей i, который имеет ту же самую топологию и то же число ветвей, но не обязательно то же

самое число элементов, как в Л^. Матрица инциденций А для Я, очевидно, та же самая, что и для Л^, т. е. А=А. Следовательно Ai=Ai = 0. Теперь можно записать, что

Vi = (А^v )hi = 0. (2)

Проводя преобразования, аналогичные предыдущим, получаем группу выражений

vi = r v = v4= iv = 0. (3)

Отсюда следует теорема Теллегена, согласно которой мгновенная сумма произведений напряжений ветвей (или их токов) цепи на соответствующие токи ветвей (или их напряжения) топологически эквивалентной цепи Й равна нулю.

Пример 3.7-1. Пример применения теоремы Теллегена. Рассмотрим цепь N на рис. 3.7-1,а. Если на входе ее в момент t=0 приложено ступен-

* Используемая здесь матрица А называется иногда укороченной матрицей инциденций, так как в ней отсутствует узел, соответствующий общей точке ( земле ).

чатое налряжение с амплитудой 2 В, то при Иулевьи начальных условиях с помощью (Программы анализа цепей найдем:

2(0 = - е-

-е-е'+2.

h (0=- е- - - е- Ч-1 : t-a = -5- е- + -g- е-е' ;

2 2 2 12

is (О = -7- е--- е-е<; t = е- + е-в'.

Рассмотрим теперь схему Я на рис. 3.7-1,6. Она имеет те же топологию и Ч:Исло ветвей, но элементы в ветвях различны. Для нее находим (для любого момента .времени):

i =(-1,1,3/2, -1/2, -1/2); V =(4.1,3,-1,4).

(5>

1 1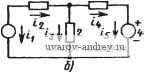

Рис. 3.7-1. Схемы цепей, иллюстрирующие теорему Теллегеиа в примере 3.7-1. Значения элементов даны в омах и генри

Легко показать, что все произведения, заданные в (3) для этих двух цепей, должны быть равны нулю. ♦

Теперь введем понятие присоединенной цепи. Прежде всего, заметим, что соотношения, определенные теоремой Теллегена (3), применимы также и к преобразованным переменным, т. е. можно i написать:

v4 = FV= V4 = rV = 0, (6)

где путем использования заглавных букв показано, что данные величины Ур являются функциями комплексной частотной переменной s. Рассмотрим

тейерь две цепи N r N, яз которых р^о --. удалены все независимые источники, 3 р^ удалены^все незТви- чтобы сформировать внешние пары шмые источники

важимов, как показано на рис. 3.7-2. Пусть Vp и 1р - векторы

соответствующих переменных на зажимах цепи Л^, а Vp и 1р- .аналогичные векторы, но для цепи N. Тогда с помощью приведенных ниже соотношений определяются матрицы полных сопротивлений Zx.x и Zx.x разомкнутой 2/г-полюсной цепи и матрицы пол-яых проводимостей Ук.з и Fk.3 короткозамкнутой 2п-полюсной щепи:

Vp--Zj. J. Ip ;

Ir,= --Y ,V,

k.3 Vpi

где знак минус определяется только выбранным направлением переменных на зажимах (см. рис. 3.7.2). Предположим теперь, что зависимые источники ветвей имеют переменные Уь и \ь для цепи

N ц Vb и h для цепи N. На основании этого можно определить

з^атрицы полных сопротивлений ветвей Zb и Хь, а также матрицы

;яолных проводимостей ветвей Уь и с помощью следующих соотношений:

Vb=bh; Vb = ZbIb; Ib = Yj,Vi,; h (8)

Для некоторых конфигураций цепи одна или обе эти имитанс-шые матрицы могут не существовать. В таком случае добавление выбранных паразитных элементов позволит обойти эти затруд-шения. С другой стороны, для установления соотношений между переменными данных ветвей можно использовать гибридную мат-дзицу. Для цепи ее можно представить в виде

Аналогично для можно записать

(10)

Предположим далее, что управляющие ветви для управляемых источников должны быть либо разомкнутыми схемами (при управлении напряжением), либо короткозамкнутыми (при управлении током) Если теперь цепи N п N линейные инвариантные во времени, то их называют присоединенными (друг к другу), если удовлетворяются следующие условия:

1. Эти две цепи имеют одни и те же топологию и упорядочение ветвей; тем самым две матрицы инциденций окажутся равными, а именно А=А. Следовательно, теорема Теллегена применима к переменным напряжения и тока ветвей этих двух цепей.

2. Матрицы полных сопротивлений ветвей и матрицы полных

проводимостеи ветвей для этих двух цепей являются перестановочными, т. е

Zj=Zb; У1%. (11)

В результате выполнения этого требования две цепи окажутся идентичными, если они не содержат управляемых источников Как следствие указанных требований, можно показать, что

YL3=Y ,. (12)

Если используется гибридное представление, то соответствующее требование примет вид

Н21 Н22 J

(13)

Ни - Hi - Н12 HJ2-

3. Соответствующие независимые источники в обеих цепях; относятся к одному и тому же типу, т. е. являются либо источниками тока, либо источниками напряжения, но не обязательно*, чтобы их токи или напряжения были одинаковы.

Второе требование, приведенное выше, содержит необходимую информацию для проектирования присоединенной цепи А? по известной исходной цепи Л^. Прежде всего, дублируются пассивные RLC-элементы, так как они представляют собой диагональные элементы в матрицах 2ь и \ь- Информацию об управ^ ляющих источниках можно получить, анализируя структуру исходных Zb, Y или других матриц. Например, ИТУН с коэффициентом усиления g, управляющее напряжение для которого снимается с ветви t, а выходной ток соответствует ветви / в цепи будет представлен в матрице \ь элементом yij=g. Следовательно,

в Yb необходимо иметь yij=g. Это будет соответствовать ИТУН с управляющим напряжением, снимаемым с ветви / и выходом, соответствующим ветви i. Легко получить соотношения и для других типов элементов. Наиболее важные из них приведены в табл.. 3.7-1. Пример использования соотношений табл. 3.7-1 показан-на рис. 3.7-3. На рис. 3.7-За приведена схема исходной цепи на рис. 3.7-36 - присоединенной цепи.

Используем теперь теорему Теллегена и понятие присоединенной цепи цля определения чувствительности. Пусть вектоо токов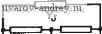

VsCp Y,.JVo yg/ VsK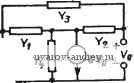

a) SJ

Рис. 3.7-3. Схемы цепей: a - исходной; б - соответствующей ей присоединенной цепи

Таблица 3.7-1 Элементы присоединенной цепи

А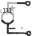

I В исходной цепи Л^ состоит из двух составляющих: вектора токов через внешние зажимы !р и вектора токов в ветвях h. Используя аналогичное представление для вектора напряж:ений V цепн N, а также соответствующих векторов токов и напряжений

I и V в цепи N, можно записать: ,х^(1.,х). V=(Vj,vp;

= V- = (V.V?). (14)

Пусть теперь значения элементов исходной цепи претерпевают случайные изменения. Тогда результирующий вектор токов можно записать как 1 + Л1. На основании закона Кирхгофа для тока имеем А(1+Л1)=0, а следовательно, получаем, учитывая, что А1 = 0:

АА1 = 0.

(15)

Таким образом, вместо I в любое из соотношений (6) можно подставить AI. Точно также в эти же соотношения можно подставить AV вместо V. Проводя такие подстановки и используя (14), получаем

>- I--о

VjAIp + VlAIb = 0; IAVp+lUVb-O. (16)

Вычитая приведенные выше равенства, находим

А 1р- 1; А\р + \1А 1ь- 1 АУь = 0. (17)

Из (7) и (8), используя приближение первого порядка, имеем

А Vp = - А (Z , 1р) = - А 1р- Z,., А 1р ; AVb = A(Zb Ib) = AZbIb+ZbAIb.

(18)

Подставляя полученное в (17) и проводя упрощения, нахо-

дим

ipMZ,.,Ip= II AZblb. (19)

Кроме того, проводя аналогичные преобразования, получаем

VAY .,Vp = VlAYbVb. (20)

Уравжния (19) и (20) устанавливают четкие соотношения ме-ШДУ изменениями значений элементов ветвей и изменениями значений параметров 2п-полюсника. Например, из (19) вытекает, что если воздействие приложено только к паре зажимов / цепи

и к паре зажимов i цепи Л^, то можно, используя в качеств ; воздействия единичные токи, записать

4 = 0; /, = 1; /, = 0.

(21)

Тогда (19) примет вид

ll А Zb lb,

(22)

где lb и lb - токи ветвей в цепях N и N соответственно, которые возникают в результате указанного воздействия. Следовательно, проведение анализа только дважды: один раз для f! и другой - для N, дает возможность получить все чувствительности для функции цепи Zfj.

Пример 3.7-2. Определение чувствительности с помощью присоединенной цепи. Пусть для цепи на рис. 3.7-4,а требуется найти чувствительности входного сопротивления Re по отношению к элементам цепи Ro, Ri, Rs и Rs-Чтобы сделать это, перерисуем цепь так, так показано на рис. 3.7-4,6. Используя программу анализа схем для входного тока /pi = l, получим вектор токов ветвей в виде (-1, -1, -6/5, 1/5, 1/5). Присоединенная цепь, сформированная на основе табл. 3.7-1, показана на рис. 3.7-4,е. Для входного

тока 7pi.= l находим вектор тока ветвей Г'=( -1, -1, 3/5, -2/5, -2/5). Тогда матрица приращений полных сопротивлений ветвей

Д/?1 О О О О

Д Zu =

О О

О О

О о о Д/?з О О

о о о

о

о о

о AR,

Следовательно, из (19) получаем

Д^?вх=Дгц = Д/?1-Ь

18 2 2

-AR..--AR.-\-~ARo.

(23)

(24)

Отсюда в предельном случае, когда приращения стремятся к нулю, находим

dRi dRB dRi

dRs 25

dRBx

(25)

Указанные чувствительности, очевидно, легко найти, используя соответст-аующие частные производные. Эти результаты мо;кпо подтвердить непосред-ствеиньим анализом исходной цепи, ф

Заслуживают внимания некоторые моменты приведенной выше процедуры, в которой для вычисления чувствительности используется присоединенная цепь. С вычислительной точки зрения метод превосходен, так как требует только двух анализов заданной цепи для вычисления чувствительности иммитансных функции заданной цепи, безотносительно к числу элементов этой цепи.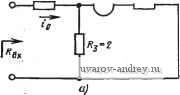

/?,=/

1Ы

+ -t- I/,

ы

о-о-

+ - +-

Рис. 3.7-4. Использование пpи^-.соединенной цепи для определе>-ния чувствительности в примере 3.7-2. Сопротивления даны в:

Кроме того, полученные результаты точны, т. е. получаются точные значения частных производных. Эту процедуру легко распро>-странить на случай устойчивого состояния при наличии гармонического воздействия, когда вычисление чувствительности проводится на заданной частоте [20, 21]. В таком случае частотно-зависимые элементы в матрицах иммитансов ветвей также должны рассматриваться как частотно-зависимые; следовательно, частотная зависимость должна присутствовать и в матрице приращений иммитансов ветвей. Например, ветви с полным сопротивлением Z=]aL будут представлены в матрице приращений полных сопротивлений ветвей членами вида: AZ=jtuAL. Однако множитель jo следует убрать для получения частной производной по L.

3.8. Выводы

В этой главе были рассмотрены вопросы чувствительности. В частности, в § 3.1 были получены важные общие соотношения, применяемые к функции относительной чувствительности любо-

Кроме указанной процедуры, основанной а методе присоединенных цепей, существует ряд других niponeflyp, основанных на методе преобразованных цепей Быховокого, методе точек чувствительности Кокотовича, методе сигнальных направленных графов и др. - Прим. ред.

ro типа. В § 3.2 было рассмотрено понятие чувствительности функции цепи в целом. Было показано, что для s=jco такая чувствительность функции цепи имеет вещественную часть, которая определяет чувствительность модуля функции, и мнимую часть, определяющую чувствительность фазы функции. В этой главе были исследованы и другие типы чувствительности: чувствительность коэффициентов (§ 3.3), ненормированная чувствительность корней (§ 3.4), чувствительности Q и (On, нормированная чувствительность корней (§ 3.5) статистическая многопараметрическая чувствительность (.§ 3.6). В результате исследования свойств различных типов чувствительностей было показано, что между ними существует взаимосвязь - например, если известна чувствительность коэффициентов, то можно вычислить чувствительность функции цепи. Наконец, в § 3.7 было показано, как вычислить чувствительность, проведя при этом анализ только два раза: один раз для исходной цепи, другой - для присоединенной цепи.

Важно выяснить, вместе с тем, как допуски на отдельные элементы активного фильтра связаны с допусками на характеристики цепи в целом. Чтобы проследить это, предположим, что такой характеристикой является у и пусть Xi{i=l, 2, .... п) -отдельные элементы данной цепи. В этом случае

y = f(Xi,X2,...,xJ. (1)

Тогда можно записать вйражение для полного дифференциала:

dy=Kdx,+ - dx, + - -Ь (2)

dxi дх2 дхп

Относительные изменения у можно найти, используя многопараметрическую чувствительность, определенную в (16), § 3.2. Тогда

dy I ( df dxi ,df дх2 df dxn

- = ------h X2 - 1- ... -t- Xji---

у у \ dxi Xi dxz X2 dXn Xn

S</ *-1-5г/ .+...-1- ЗУ (3)

Xi X2 Xn

где dxilxi (t=l, 2, n) - относительное изменение элемента Xi.

Пример 3.8-1. Допуск на величину резонансной частоты. Задана функция цеои, имеющая в знаменателе полином вида (s-f-(£o /Q)s-l-£o ). Схем-иая реализация этой функции такова, что cun=4ARC, где R имеет допуск ±5%, а С -допуск ±10%. В соответствии с указанным выше, найдем

Таким образом, относительное изменение Шп в расчете на худший случай составит ±0,15 или 15%. ♦

Паразитные составляющие неидеальных пассивных компонентов активных фильтров могут быть обусловлены различными факторами: границами допусков, температурной зависимостью, паразитной частотной зависимостью и шумами. Среди них наиболее важную роль играет температурная зависимость как для сопротивлений резисторов, так и для емкости конденсаторов. Кроме того, для конденсаторов наличие шунтирующего сопротивления утечки, определяемого тангенсом угла потерь, может привести к нелинейной частотной зависимости. Для резисторов более важными могут оказаться шумы.

Эта зависимость отдельных элементов цепи от любых паразитных составляющих, указанных выше, может оказать влияние на характеристики цепи в целом, причем масштаб этого влияния определяется значениями этих элементов. Чтобы показать это, рассмотрим еще одну характеристику цепи у, которая является функцией значений элементов Xi, Х2, как показано в (1). Если элементы х зависят от некоторых паразитных составляющих неидеальных элементов, обозначенных через z, то у также является функцией Z. Разделив (2) на dz, получим

dydl dxj j dx2 j dxn

dz dxi dz dx2 dz dXn dz

Как правило, зависимость у or z считается эффектом первого порядка и выражается как относительное изменение у на единицу Z, обозначаемое обычно в миллионных долях на единицу z. Умножая левую и правую части (5) на \\у, получаем математическую формулировку такой зависимости в виде

= J (6)

dz у \ dxi dz дх2 dz дхп dz j

Эту общую форму можно использовать для оценки относительного изменения функции у в зависимости от параметра z.

Пример 3.8-2. Температурная зависимость усиления усилителя.

Конечный коэффициент усиления усилителя определяется как iC=l+J?2№i. Если номинальные значения R2 и \Ri зависят от температуры, то желательно найти относительное изменение К ъ миллионных долях/ С Предположим, что K=IG и \Ri={ кОм. Тогда J?2=9 кОм, откуда /(=10. Пусть, кроме того, паразитная температурная зависимость R и R2 определяется следующими значениями: d;?,/dr=2000-10-V°C и dR2ldT=\0(X)-\Q-r С. Тогда из (6) следует:

dKIK 12 dRilRx R2 dRlRX dT ~ К\ Ri dT Ri dT )

-[--) = -)=~--У'С- ♦

В табл. 3.8-1 и 3.8-2 приведены некоторые свойства резисторов и конденсаторов различного рода. Из них металлопленоч-ные резисторы широко используются для реализаций активных фильтров. Из указанных типов конденсаторов обычно используют-

ТаЗлица S.8-1

Типичные характеристики резйс*орбб, широко иепоЛьзуемых в акгийиых фильтрах

Характеристика

ТолстопленочныГ! металлокерамика

Тип резистора

Тонкопленочный

Нитрид тантала (оксийитрид)

Специальный

Дискретный

Проволочный

На углеродистом составе

Металлопленоч -ный

На углеродистой пленке

Температурный коэффициент 10-ТС

Температурный диапазон линейности ТКС, С

Диапазон .номиналов со-]противлений. Ом

Достижимая точность, %

Старение, %/20 лет

Максимальное значение, Ом/еднницу площади

Примечание

-МОО

Нелинейный

3 Ом ... 1 МОм

0,5 1,0

Специальные краски и обработка могут улучшить устойчивость и точность

-100±20 (-200+20)

0...100

10 Ом ... 1 MOi

0,1 0,1

- 10 -55.. + 125

100 Ом ... ... 0,3 МОм

0,02 0,01

±10- ГС и старение 10-10-*/год (возможные значения)

+ 25... +85

100 Ом... ... 100 КОм

0,01

0,01

Специальные методы намотки могут уменьшить индуктивность

-1500

Нелинейный

10 Ом ... ... 2 МОм

5,0 5,0

0... -f50 -f 25...-f 85

10 Ом .. 1 МОм 0,5 0.1

Старение 0,1 и ТКС= =-±10-ТС (возможные значения)

0...-f 50 Нелинейный

10 Ом ... 2 МОм 1,0 2...5,0

Взято из работы Су 122],