2-23 (§ 2.5). Используя выражение, приведенное в (22) § 2.5 определите коэффициенты лолияома знаменателя функции цепи для фильтра Томсона четвертого порядка. Проверьте шравильность результата, используя тавл. 2.S-1.

2-24 ( § 2.5). Используя выражение, [приведенное в (23) § 2.5, определите коэффициенты полинома знаменателя функции цепи фильтра Томсона пятого торядка. Проверьте правильность результатов, используя табл. 2.5-1.

2-25 (§ 2.5). а) Определите требуемый поря1ДОк функции цепи, имеющей ГВП 1 мс ic ошибкой не больше 2,5% и амплитудными потерями не больше 3 дБ для Всех частот вплоть до 1500 рад/с.

б) Реализуйте указанную функцию цепи в Виде передаточной проводимости, используя лестничную цепь .без потерь с одним нагрузочным сопротивлением 1 кОм.

2-26 (§ 2.6). Для функции цепи W(s) = (2s-l-3)/(s-l-l) (s-1-2) .найдите время нарастания tr и ширину полосы на уровне -3 дБ с и сравните произведение этих величин со значением, указанным в (5) § 2.6.

2-27 (§ 2.6). Решить задачу 2-26 для функции цепи вида N(s) = = l/(s2+s+il).

ЧУВСТВИТЕЛЬНОСТЬ

Одна из проблем, с которой постоянно сталкивается разработчик, состоит в оценке полученной реализации, особенно в сравнении с другими возможными реализациями, которые удовлетворяют тем же самым техническим требованиям. Для того чтобы сделать это, разработчик должен воспользоваться понятием чувствительности фильтра. Под чувствительностью понимают меру изменения некоторой характеристики цепи (или .функции цепи), которое произошло в результате некоторого отклонения одного или нескольких элементов цепи от их номинальных значений. Даже если реализация цепи привлекательна с теоретической точки зрения, она может быть практически бесполезной, если ее чувствительность высока. Таким образом, при проектировании фильтра разработчик должен быть заинтересован не только в том, чтобы выбрать реализации, имеющие низкую чувствительность, но и в том, чтобы минимизировать чувствительность тех реализаций, которые он хотел бы использовать. В этой главе мы столкнемся с примерами решения этих двух задач.

3.1. Относительная чувствительность

Для обозначения чувствительности используется символ S. Кроме того, используются верхние индексы, чтобы указать, чувст-ьвительность какого параметра оценивается, и нижние индексы,

для указания того элемента цепи, который явился причиной изменения данного параметра. Если в качестве параметра взять у, а элементом, вызвавшим изменения, считать х, то можно определить относительную чувствительность следующим образом:

дх у дх/х д (1п х)

Существует множество вариантов выбора параметра у. Им может быть, например, функция цепи (как функция s или о), или же в качестве него могут выступать положения полюсов (нулей), определенные коэффициенты функции цепи, отдельные параметры, такие как добротность Q функции цепи и т. д. Как использовать различные типы чувствительности, будет показано в следующих параграфах этой главы. Здесь же рассмотрим некоторые свойства, характерные для любой чувствительности, определенной выражением (1). Эти свойства пронумерованы и сведены в табл. 3.1.1.

Свойства 1 и 2. Чувствительность любого произведения параметра на постоянную равна чувствитлеьности исходного параметра. Чтобы показать это, запишем

kydjky) X d{ky) ду X . 2

* дх ky ду дх ky

где k не является функцией х. Аналогично, 8Уьх=8Ух.

Свойство 3. Чувствительность к изменению обратной величины равна чувствительности к изменению исходной величины, взятой с обратным знаком. Чтобы показать это, запишем

gy ду 1/х ду дх ду х

д(1/х) у дх д{1/х) у дх у

Аналогично 8х^у=-5Ух.

Свойства 4-9. Чувствительность произведения параметров равна сумме чувствительностей отдельных параметров. Чтобы показать это, запишем

(УхУг) У^ду! X J yidy

дх УгУ2 дх у^у^ дх , у^у^ ах У1 дх У2

Распространяя это свойство, можно показать, что чувстви тельность параметра, возведенного в п-ю степень, равна произведению показателя степени на чувствительность исходного пара-**етра, т. е. 8у х=п8Ух. Аналогично, 8Ух - =8Ух/п.

Свойства 10 и И. Чувствительность отношения параметров равна разности чувствительностей исходных параметров. Исполь зуя свойства 3 и 4, получаем

Sii = S4-Sy.! = S?-S?=. (5

Свойства функций относительной чувствительности

* в этом соотношении у - комплексная, ад: - вещественная величины.

Свойства 12-14. Чувствительность комплексного парамеТ' ра также является комплексной величиной. Вещественная часть является чувствительностью модуля, мнимая часть соответствует чувствительности фазы, умноженной на фазу (предполагается, что X вещественно).

Пусть Y - модуль у, а ф - фаза у. Таким образом, y=Yeif. Используя (1) и свойство 4, получаем

Sr=Sr 4-Sf = sr =sr +j = sr +]ф5Г (6)

Табл. 3.1-1, кроме соотношений, полученных выше, содержит и некоторые другие полезные формулы.

При синтезе пассивных или активных фильтров любого типа неминуемо возникает проблема минимизации чувствительности. Для случая, когда у является линейной функцией х, легко получить

-A- -is?(I- ). ,7)

В этом случае производная функция чувствительности легко оценивается и не требует дифференцирования. Аналогичная ситуация (хотя при этом получаются более сложные выражения) возникает при нелинейной зависимости у от х (см. задачу 3-2).

3.2. Чувствительность функций цепи

В этом параграфе введем первую специальную функцию чувствительности, соответствующую форме относительной чувствительности, определенной в (1), (см. § 3.1). В качестве параметра у в этом соотношении выбрана функция цепи N{s). В качестве х обычно выбирается какой-то активный или пассивный элемент схемной реализации этой функции. Такая чувствительность называется чувствительность/о функции цепи. Она определяется следующим образом:

cNHs) dN (s) X ...

дх N{s)

Если функция цепи записана в виде отношения полиномов A{s) и B(s), т. е.

N{s) = A{syB{s), (2)

то можно получить следующую удобную формулу (1):

= X [А' {s)/A is)-B is)/B (s)], (3)

где A{s)=dAis)/dx; В'{s) =dB{s)/dx.

Рассматривая установившееся состояние при гармоническом Воздействии и применяя свойство 12 (см. табл. 3.1-1), находим

oW(ito) oJV(](o) I gargjV(jco)

* Она часто называется классической чувствительностью или чувствительностью по Боде. Впервые она была Я|редставлена в работе Боде [9] ib виде <оотноц1еиня, обратного данному.

Другую форму этого выражения, которая часто оказывается полезной, можно получить при использовании таких понятий, как частотные зависимости затухания а (ко) и фазы Р(а)):

a(a)) = l/lniV(jft)); р (и) = arg (j ш). (5) Используя их, можно записать

сЛ (] о) да{<а) . . gp(<a)

dxlx dxlx >

Таким образом, вещественная часть чувствительности дает изменение функции затухания, а мнимая часть - фазовую характеристику, в обоих случаях по отношению к изменению нормированного значения элемента.

Пример 3.2-1. Чувствительность функции цепи для пассивной RLC-цепи. В качестве примера вычисления чувствительности функции цепи рассмотрим последовательную iLC-цепь (рис. 3.2-1). Для этой цепи

У (S) = S (11 mis + S {RIL) + 1/Щ. (7)

Рис. 3.2-1. Схема il-Счцепи, используемой в примере 3.2-1. Значения в омах, генри, фарадах

г=/ /?=/

/r= j =

Применяя (3), находим

Sl< = -sy[s + s {RIL) + I/LC] ; S() = (1 /LC)/[s2 + s (RID + 1 ILC\ ; (8)

.Анализируя далее чувствительность к R путем подстановки номннальныл значений элементов, локазанных на рис. 3.2-1, и полагая s=jm, получаем

5V(J СО) = 2/{(3 2)2 , £,2] + j [ <в (3 -0)2)]/[(3 £o2)2 2]. (9)

Графики .модуля и фазы функции цепи для значений R, равных I и 1,1 Ом, и соответствующей чувстюительности (для R=l Ом) показаны на рис. 3.2-2.

Важно уяснить, что соотношения, определяемые с помощью функций чувствительности, являются точными только тогда, когда рассматриваются бесконечно малые приращения; тогда, используя (4), для случая x=R можно записать

d arg (j (О) = Im dR/R;

d\N(ia>)\l\N{]ay)\=ReSUR/R. (10)

Если используются конечные приращения, т. е. если dargNda), d\N{i(x>) \ к dR в (10) заменяются на AR, AargAf(j(o), A\N{i<o)\, то указанные соотношения нужно рассматривать как приближенные. В подтверждение этого отметим, что если оценить чувствительность к R, заданную выражением (9), на частоте

=2 рад/с. то получим 5нУ<12)= 0,8+] 0.4. Если же фактически изменим /? на 107о, т. е. например, до величины 1,1, и рассмотрим фактические изменения модуля и фазы Y{j2), то получим значение чувствительности -0,747-fj 0,369. Как только процентные из-ленения R становятся меньше, данные значения приближаются к указанным выше.

Другое интересное наблюдение, касающееся функций чувствительности, связано с обобщенной полосовой функцией цепи второго порядка. Она имеет вид

N(s) = as/{s + bs + bo). (11)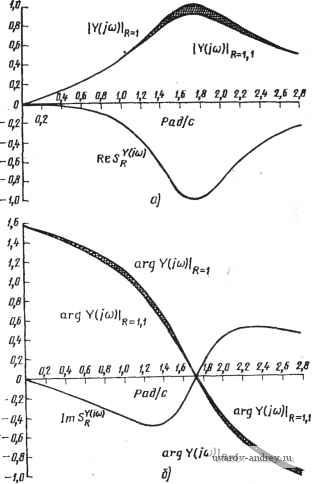

Рис. 3.2-2. Чувствительности функций цепи, приведенной а рис. 3.2-1: *[ -модуль функции цепи и вещественная часть чувствительности для этой нкции; б-фаза (аргумент) функции цепи и мнимая часть чувствительности для этой фзщ'кции (фазы приведены в радианах)

Ее чувствительность по отношению к комплексной частотной переменной s, как это нетрудно видеть, равна

\ CiS s + bis + bo J s + bis + bo

Оценивая значение чувствительности на резонансной частоте, т. е. в точке s=j находим

>U, VK = 5= - j 2 = - j 2 Q. (13)

где второй член получается как результат применения свойства / (см. табл. 3.1-1), а добротность цепи Q определяется как^

Q = Vhlb. (14)

Таким образом, чувствительность функции цепи по отношению к комплексной или вещественной частотной переменной является чисто мнимой в точке резонанса. Применяя (4) к указанной выше функции цепи, получаем

(а=УЬо д со/и

= -2Q. (15)

Эти результаты показаны на рис. 3.2-2.

Анализ чувствительности функции цепи, проведенный в этом параграфе, легко распространить на случай, когда определяется влияние на функцию цепи более чем одного параметра. В этом случае выражение (1) в § 3.2 можно записать в виде

~=[ыыш-р^1, (16)

где п - число рассматриваемых элементов. Используя (4), можно заметить, что

d\N(i(u)\ ynggW(]co) dxt

d arg (3(0)) =2 ImS.i-. (18)

Таким образом, в (16) дана компактная оценка изменения как модуля, так и фазы. В качестве иллюстрации этого, можно найти для примера 3.2-1 чувствительность ко всем трем элементам в точке резонанса ((о=1/3): 5л^ з ) = ! ru/F) =

Добротность Q более Полно обсуждается в § 3.5.

В !ряде отечественных работ, например в [1*], добротность определяется .как 2\/%/bi. - npuM. пер.

в результате получаем

dY{s)

s=j V 3

lK(jV3)i

= (-i)+(-iK3)-+(-jT/3)

(19)

I . с

Используя результаты, представленные в (19), можно указать на другие особенности, связанные со схемой на рис. 3.2-1, а именно: в точке резонанса изменение значений L или С не влияет на модуль функции цепи и максимальная чувствительность по отношению к R равна единице. В § 3.6 рассмотрим многопараметрическую чувствительность более подробно.

Для случая влияния многих параметров имеется и ряд других полезных применений чувствительности функций цепи. В первую очередь это относится к определению отклонения АЧХ данной реализации цепи от номинальной в расчете на худший случай, когда элементы цепи имеют предписанный допуск. Если обозначить номинальное значение каждого из п элементов х как х^ , то можно определить поле допуска следующим неравенством:

(1-е)х^хГ{1+г), i=l,2.....и. (20)

Из (16) видно, что худшим случаем будет такой, когда все элементы примут свои крайние верхние или крайние нижние значения, что соответствует граничному значению поля допуска е. При этом, конечно, предполагается, что рассматриваются эффекты первого порядка. Следовательно, можно определить чувствительность модуля в расчете на худший случай W J*)) I с помощью соотношения

(21)

Максимальное отклонение от номинальной характеристики, т. е. характеристика, которая получилась в результате того, что элементы приняли свои крайние значения, определяется в результате как eWi J*) I. Для других значений элементов цепи Хи удовлетворяющих (20), АЧХ будет лежать в определенных границах, как показано на рис. 3.2-3. Аналогичную процедуру можно

Рис. 3.2-3. Чувствительность модуля фуинции цепи в расчете на худший случай:

/ - верхний предел максимального отклонения; 2 - номинальное значение; 3 - нижний предел максимального отклонения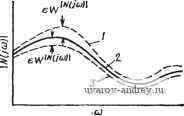

использовать для определения фазовой чувствительности в рас-счете на худший случай.

Для некоторых классов цепей можно показать, что амплитуд, пая чувствительность для наихудшего случая имеет нижнюю границу. В качестве примера рассмотрим цепь, пассивными элементами которой являются сопротивления, емкости и идеальные трансформаторы, а активные элементы представлены гираторами, КОС, ИТУТ, ИНУН. ИТУН и ИНУТ . Для такого класса цепей можно показать, что для любой безразмерной передаточной функции T{s)

(22)

S5j/>=25r<>.

i

где Xi включает только такие пассивные элементы, как сопро-тивление и емкости, и такие активные элементы, как ИНУТ и гираторы. Это выражение можно переписать в виде

2=5 и 2 Si

(23)

(24)

Применяя (21) к полученному выше, имеем

Сравнивая первый и последний члены этого выражения, можно определить нижнюю границу LW I -Cia) чувствительности модуля в расчете на худший случай [10]:

lj7ini ,i 25ir(]co,i 25)

Из правой части этого уравнения следует, что нижняя граница зависит только от функции цепи T{s) и, таким образам, не зависит от конкретной техники синтеза, используемой для реализации функции цепи. Аналогично этому можно получить нижнюю границу для фазовой чувствительности, рассчитанной на худший случай.

Чувствительность функции цепи применяется еще и тогда, когда хотят использовать машинные программы оптимизации для выбора значений элементов так, чтобы одновременно минимизировать чувствительности цепи к изменению всех элементов. Процесс оптимизации минимизирует, как правило, скалярную функцию, указывая уровень, достигнутый при минимизации. Далее,

Используя Параметры п-ередачи четырехлолюсннка (или параметры цепной матрицы.-Яриж. пер.), а также обобщенные параметры {прим. ред.), определенные с помощью соотношений

эти элементы можно определить следующим образом: гиратор: Л=О=0, С>0, В>0; КОС (конвертор отрицательного полного сопротивления): В==С=0; (Л/С)<0; ИТУТ у4=В=С=0, ВФ; ИНУН: B=C=D=0, Аф{; (см. такжр § 6.1); ИТУН: Л=С=£>=0, Вфй; ИНУТ: Л=В=О==0, Сф.

как правило, оценивают среднеквадратичную сумму вкладов отдельных функций. Следовательно, можно определить квадратиче-скую амплитудную чувствительность Q\N{]iii)\ следующим выражением:

QA.(i (ReS/iT. (26)

Скалярную оценку можно также использовать для одновременного оценивания амплитудной и фазовой чувствительности путем определения квадратичной чувствительности в виде

(27)

1 .=1 Примеры таких типов чувствительности приведены в последующих главах.

Использование функций чувствительности дает возможность исследовать важные свойства широко используемых двусторонне нагруженных лестничных фильтров без потерь, приведенных в приложении Л. Для таких фильтров можно показать, что на любой частоте максимального усиления в полосе пропускания источник доставляет максимум полезной мощности в нагрузку. Таким образом, для любой такой частоты любые изменения как в сторону увеличения, так и в сторону уменьшения номинальных значений любых элементов L или С могут привести только к уменьшению усиления. В результате этого, если рассмат-ривакется эффекты только первого порядка, чувствительность амплитуды, т. е. вещественная часть функции чувствительности, должна быть равна нулю [12].

В качестве примера рассмотрим широкополосный ПФ (рис. 3.2-4,а). Обозначим его передаточную функцию по напряжению через N{s) = V2is)IVi{s). Как видно из АЧХ фильтра, приведенной на рис. 3.2-4,6, его средняя частота равна 1 рад/с, ширина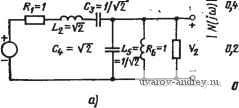

CJ, рад/с 6)

Рис. 3.2-4. Широкюиолосный ПФ четвертого порядка: -схемная реализация; значения элементов даны в омах, генри, фарадах;

б - АЧХ фильпра.

Впервые предложена Скеффлером [41] и иногда называется чувстви-льностью по Скеффлеру.