Изучение почти любой области техники: электротехники, механики, гидравлики, теплотехники и т. д., всегда можно разделить на две части - анализ и синтез. При анализе имеют дело с нахождением характеристик или свойств какой-то уже существующей системы. Этот процесс иллюстрируется структурной схемой на рис. 1.1 - 1,а. Ее можно прочитать так: Задана система, требуется найти ее свойства . Часто, конечно, система может существовать только как схема, показывающая взаимные связи идеализированных- элементов. В этом случае схема определяет модель системы, а анализ в силу этого определяет свойства данной модели. Если такая система (или модель) описана полностью, то ее свойства, конечно, однозначны. Следовательно, в задаче анализа существует Т'олько одно решение.

При синтезе имеют в качестве исходного желаемый набор свойств, и цель состоит в том, чтобы найти систему в ее фактическом виде или (как это чаще бывает) в виде модели, которая имеет такие свойства. Этот процесс иллюстрируется структурной схемой, на рис. 1.1 - 1,6. Ее можно прочитать так: Задан набор

Система 1

Система!

Свойства

Рис. 1.1-/. Структурные схемы: а -анализа; б - синтеза

свойств, найти систему, которая ими обладает . В общем случае, как это и показано на схеме, существует обычно больше, чем одна такая система. Следовательно, в задаче синтеза решение редко бывает единственным. Как следствие этой неединственности, в процессе синтеза требуется конечный этап, а именно: оценка нескольких различных систем, каждая из которых имеет желаемый исходный набор свойств, с целью выделить среди них наилучшую. Прежде чем можно будет сделать это, следует определить, что подразумевается под словом наилучшая. Другая возможность ра-

зобраться в данной ситуации состоит в том, чтооы дополнительно К: исходным заданным свойствам рассмотреть еще одно или несколько свойств, что позволило бы сделать выбор среди полученных систем. Очевидно, что процесс синтеза значительно более сложен, чем процесс анализа!

Цель книги состоит в том, чтобы исследовать синтез особого класса систем, а именно: фильтров для электронных схем. Такие фильтры широко используются в современных системах связи и обработки сигналов. В самом деле, трудно найти даже не очень сложное электронное устройство, которое не содержало бы один или несколько фильтров. В процессе изучения фильтров будем заниматься поиском способов соединения элементов цепи, которые позволили бы реализовать схему, обладающую определенными характеристиками фильтрации. Для достижения этой цели необходимо рассмотреть несколько вопросов. Один из них - такое определение методов выражения или аппроксимации свойств фильтров, которое облегчает их синтез. Этот вопрос составляет содержание задачи аппроксимации. Другой полезный вопрос - развитие методов исследования изменений свойств заданных реализаций фильтров в результате вариации расчетных значений их элементов. Эти вариации могут быть вызваны старением, температурными изменениями, допусками на параметры компонентов и т. д. Это - основной вопрос темы чувствительность, которая дает ценные технические приемы для сравнительной оценки схем фильтров, хотя и различных по форме, но имеющих аналогичные свойства. Еще один круг вопросов, который рассмотрен здесь, - изучение элементов активных цепей. Фильтры, построенные на основе таких элементов, часто имеют существенные преимущества по сравнению с фильтрами на пассивных элементах. В последующих главах эти вопросы, а также ряд других, будут рассмотрены так, чтобы дать читателю исчерпывающую и единообразную трактовку современных методов синтеза активных фильтров.

1.1. Функции цепи

В этом параграфе дадим краткий обзор основных концепций теории цепей. Дополнительные обсуждения этих концепций можно найти в работах, указанных в списке литературы.

Обычными переменными, которые ассоциируются с электронными схемами, являются напряжения и токи, измеренные в различ-иых точках этих схем. Они являются физическими или реально существующими переменными в том смысле, что их можно измерить с помощью измерительных приборов или отобразить на экране осциллографа, а если они достаточно велики, то могут вызвать лоявление осязаемых признаков своего присутствия, таких, напри-i мер, как искра или удар. В подавляющем большинстве случаев использования фильтрации значения этих переменных не постоянны, а изменяются во времени. Следовательно, мы записываем их в форме v{t) н i(t) и относимся к ним как к переменным, опреде-

ленным во временной области. Временное определение характеристик фильтрации представляет собой описание того, как возникает некая реакция (или выходной сигнал), переменной {t), которая может быть напряжением или током, в результате воздействия (или подачи на вход) переменной e{t), которая, в свою очередь, может быть напряжением или током. Определение соотношений между входными и выходными переменными, если они являются функциями времени, является в вычислительном аспекте занятием достаточно утомительным, так как приводит к необхо димости решать интегродифференциальные уравнения и не дает возможности проследить, каким образом различные элементы данной цепи влияют на данное соотношение. Вместо этого для схем с линейными инвариантными во времени элементами обычно используют преобразование Лапласа, которое создает новые (преобразованные) переменные: R{s) -для реакции и E{s) -для воздействия. Эти переменные связаны с r{t) и e{t) следующими преобразованиями:

7?(s) = S;{r(0} = J/-(0e-d;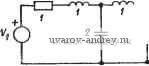

E(s)X{e{t))=le{t)~tdt, (1)

о

где S{ } можно прочитать как преобразование Лапласа от . В подынтегральных выражениях, приведенных выше, показатель экспоненты в члене е~** должен быть безразмерен. Поэтому можно

прийти к заключению, что величина s Т~% должна иметь размерность обратного Л времени или частоты. Таким образом, у г говорят, что переменные R{s) и E{s) определены в частотной области, а & называется переменной комплексной Рис. 1.1-2. Схема, функция частоты. Ее значения часто отобража-цепи для которой задана вы- ются на двумерную плоскость коми-re=U?~e,!pt --ной .шстоты. Соотношение между фарадах /<(s) и t{s) в общем случае задается

путем определения функции цепи N{s) как отношения реакции к воздействию для случая, когда все начальные условия цепи нулевые. Следовательно,

N{s)R(s)/E{s). (2)

Для примера рассмотрим цепи на рис. 1.1-2. Если определим переменную реакции как Vzis), а переменную воздействия как ¥1(5), то, используя обычные методы анализа цепей, найдем, что функция цепи

(s) = is)/V (s) = 0,5/(s3 + 2s2 + 2s + 1). (3)

Выражения в частотной области, аналогичные приведенному выше, являются наиболее общими в том смысле, что они приме-

йимы почти к любому типу возбуждающей функции во временной области. Однако чаще всего требования фильтрации основа-нй на анализе установившегося режима цепи при гармоническом воздействии. Следовательно, предполагается, что воздействие имеет вид

е(0 = К2£оС05(сй + а), (4)

где Wo - среднее квадратическое значение (cKe)e{t), © - круговая \частота в радианах в секунду и а - фаза в радианах. Для такого воздействия, предполагаем, что N{s) устойчива' после того, ккк составляющая переходного режима во временной области для r\t) уменьшилась, затухая, до пренебрежимо малой величины, r{t) будет иметь вид

; r(0 = >/?oCos((D/-fp), (5)

где Ro - среднее квадратическое значение r(t), а (3 - его фаза. В этих условиях легко найти соотношение между e{t) и r{t), если использовать комплексные числа, названные фазорами, для представления гармонически изменяющихся величин. Для фазоров, соответствующих e{t) и r{t), будем использовать символы и 5?:

eEoei; J = R,ei. (6)

Соотношение между фазорами и 5? получается непосредственно путем замены переменной s в выражении (2) для функции цепи N{s) на переменную jco. В результате получаем

A(j(o) = /g = /? eiP/£oei . (7)

Часто интересуются только соотношением между средними квадрэтическими значениями гармонических сигналов возбуждения и реакции. В этом случае, взяв модули от обеих частей выражения (7), получим

\Nii(o)\ = \J%/S\ = \[/\S\ = Ro/Eo. (8)

Эти величины можно, конечно, выразить в логарифмической мере (децибелах), если взять 20 lgA(jcu) . Кроме этого, можно выразить разность фаз между гармоническими сигналами возбуждения и реакции. В этом случае, вычисляя аргументы обеих частей (7), можно записать

arg iV (j со) = arg (/g) --= arg-arg & = p-a. (9)

В качестве примера вычисления этих величин рассмотрим цепь на рис. 1.1 -2 и функцию цепи (3); в результате получим

A(jco) =0,5/[(1-2(оТ + (2со-(оЗ)2]1/2; (Ю)

arg N (] со) = - arc tg {(2©-(оЗ)/( 1 - 2©)}; (11)

Графики этих функций приведены на рис. 1.1 -3. Итак, функция цепи N(s), определенная в (2), обладает очень важным свой-

Под еловой, устойчива подразумеваем, что для любого ограниченного воздействия e(i) реакция r{t) также будет ограничена.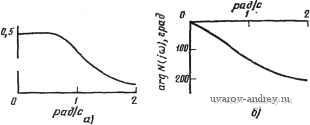

Рис. 1.1-3. Амплитудно-частотная и фазочастотная характеристики цеинУ схема которой триведена на рис. 1.1-2 /

ством, а именно: она определяет для всех частот реакцию ц^пи в установившемся режиме на гармоническое воздействие. Почти все методы синтеза фильтров используют указанную функцию цепи в качестве исходной.

1.2. Свойства функций цепи

В предыдущем параграфе было введено понятие функции цепи. Такие функции могут определяться различными путями. Самая простая ситуация соответствует случаю, когда интересуются напряжением и током как переменными цепп только на одной паре зажимов. Если принять за основу направление и полярность переменных, показанные на рис. 1.2 - 1, то такую цепь относят к разряду двухполюсников, а функции цепи называют входными функциями.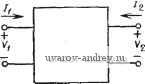

Рис. 1.2-/. Схема двухполюсной цепи

Рис. 1.2-2. Схема четырехполюснои цепи

Для двухполюсника определяются только два типа входных функций. Если ток трактуется как переменная возбуждения, то функция цепи определяется как входное полное сопротивление Z{s) = Vi{s)/Ii{s); если же в качестве переменной возбуждения рассматривается напряжение, то функция цепи определяется как входная полная проводимость y(s) ==/i (s)/Vi (s). Очевидно, У(5) = = l/2(s).

Более интересен для практических применений фильтрации случай, когда цепь имеет четыре внешних зажима. Эти зажимы размещаются так, что образуют двелтары, названные входами, позволяя, таким образом, определить четыре переменных: две - напря-

жения, две другие -токи. Примем относительные направления и Уюлярности переменных такими, как они показаны на рис. 1.2 - 2; \огда указанная цепь называется четырехполюсником. Нижние (на рисунке) зажимы двух входов часто являются общими, в этом случае цепь иногда относят к разряду трехполюсников. В дополнение к входным функциям, которые можно определить для таких четырехполюсников, может рассматриваться любая функция цепи, включающая в себя переменные с обоих входов, которая называется передаточной функцией. Такие функции могут быть переда-тоодыми полными сопротивлениями и полными проводимоетями, а также безразмерными передаточными функциями по напряжению, такими как Viis)IVi{s) или Fi(s)/V2(s), или же безразмерными перекаточными функциями по току, такими как l2{s)/Ii{s) или /i (s)l 2(s). Последнее соотношение требует наличия пути прохождения для тока реакции на воздействие. Это обычно обеспечивается либо коротким замыканием схемы, либо включением нагрузки со стороны второй пары зажимов (со стороны выхода).

В \общем случае функция цепи N(s) имеет вид отношения по-линo а Л (s) в числителе к полиному В (s) в знаменателе, т. е.

N{s) = A(s)/B{s). (1)

Нули полинома числителя A(s) называются при этом нулями функции цепи N{s); это значит, что они имеют такие значения s (называемые иначе местоположениями в плоскости комплексной частоты), при которых N{s) равна нулю. Нули полинома знаменателя B{s) именуются в этом случае полюсами функции цепи N(s). Они имеют такие значения s (или местоположения в плоскости комплексной частоты), при которых N(s) бесконечно велика. Положение полюсов непосредственно связано с фильтрующими свойствами данной цепи. Например, для устойчивой цепи полюсы ее функции цепи должны лежать в левой полуплоскости или, если они располагаются на оси jo, то должны быть простыми, т. е. быть функциями только первого порядка. Цепи, у которых функции цепи имеют полюсы в правой полуплоскости или полюсы порядка выше, чем пер1вый, на оси j to, неустойчивы, т. е. они характеризуются неограниченной реакцией при ограниченном воздействии на входе и, следовательно, не могут соответствовать физически реальной ситуации.

Рассмотрим теперь, как изменяется вид функции цепи под влиянием элементов, из которых состоит фильтр. В общем случае для линейных сосредоточенных конечных цепей A{s) и B{s) -полиномы с вещественными коэффициентами. Следовательно, функция цепи

N{s) = A {s)/B (s) = (ao + a,s + a,+...)/{bo + biS + bs + ...). (2)

В этом случае N{s) называется (вещественной) рациональной функцией, т. е. отношением полиномов. Для трехполюсной цепи, состоящей только из пассивных элементов, таких как сопротивления, емкости, индуктивности (jRLC-цепь), коэффициенты bi в вы-

ражении (2) должны быть неотрицательны, а полюсы N{s) всегда/ должны лежать в левой полуплоскости и/или быть простыми н^ си j(D. Однако, если в цепи присутствуют активные элементы, тг кие как управляемые источники (УИ), коэффициенты bi мог> быть отрицательными, а полюсы N{s) -лежать в правой Eonf-&Л0СК0СТИ. В этом случае цепь, конечно, будет неустойчива.

Можно было бы провести дальнейшую классификацию свойЛв тюлюсов N{s), если рассмотреть возможное положение этих полюсов для цепей, содержащих различные типы элементов. НапЬи-м.ер, для цепей с iLC-элементами полюсы могут располагаться в ,51юбой части левой полуплоскости и/или на оси jco. В последнем случае они должны быть простыми. Для LC-элементов полюсы будут лежать только на оси jco (и будут простыми). Для RC-j или iiL-элементов полюсы будут лежать только на отрицательной вещественной полуоси или в начале координат. Однако для i/епей, содержащих jRC-элементы и усилители (моделированные как управляемые источники), полюсы могут находиться :в любом месте плоскости комплексной частоты. Фильтры, реализованные с помощью таких цепей, относятся к классу RC-фильтров с усим теля-ми. Они дают пример класса активных фильтров или активных RC-фильтров. По существу, они обладают всеми преимуществами ILC-цепей, в том числе могут иметь любое желаемое расположение полюсов в левой полуплоскости, при этом нет необходимости иметь катушки индуктивности. Так как катушки индуктивности имеют достаточно большую массу, то их отсутствие в jRC-цепях снимает эту проблему, что очень важно, например, в космических орименениях. Кроме того, это позволяет избежать нелинейности, свойственной катушкам индуктивности при насыщении, а также их неидеальности, или рассеяния энергии из-за потерь в обмотке и сердечнике. И, наконец, катушки индуктивности, как правило, не реализуют в интегральном исполнении, в противоположность R- и С-элементам. Таким образом, активные jRC-фильтры имеют мно-

Таблица 1.2-1

Характеристики полюсов для различных классов элементов цепи

го преимуществ по сравнению с пассивными Л-С-фильтрами, за исключением тех применений, где требуется фильтровать очень большие напряжения или токи, например, в импульсных цепях ра-гаров. Кроме указанных выше /?С-фильтров с усилителями, существует несколько других типов активных /?С-фильтров, в неко-Ьрых из них используются КОБИ (конверторы обобщенного (импеданса) полного сопротивления) или операционные усилители (©У) в качестве активных элементов. Свойства функций цепи для сцм, составленных из различных комбинаций этих и других упо-М5щутых выше элементов цепи, сведены в табл. 1.2- 1.

1.3. Типы фильтров

этом параграфе приведем краткий обзор основных типов фильтров, которые будем рассматривать в этой книге. Первым из них является фильтр нижних частот (ФНЧ). По определению, свойства этого фильтра таковы, что низкочастотные составляющие сигнала, действующего на вход, вплоть до постоянного тока, переда) этся на выход, тогда как высокочастотные составляющие, вплоть до бесконечно больших частот, задерживаются. Таким образом модуль функции цепи нижних частот в идеале имеет вид, показанный на рис. 1.3- 1,а. Полоса нижних частот, которая пропускается на выход, называется полосой пропускания фильтра. Как доказано на рисунке, она равна значению наивысшей передаваемой частоты с. Эта частота называется частотой среза. На практике представленную идеальную АЧХ можно реализовать только приближенно.

Рис. 1.3-1. Вид основных АЧХ ФНЧ

Несколько вариантов такой аппроксимации показано на рис. 1.3- 1,6-д. Заметим, что в каждом случае модуль функции цепи достигает нуля только на бесконечно большой частоте. Для этих характеристик ширина полосы определяется заданием некоторого-допустимого отклонения АЧХ от ее максимального значения. Этот максимум может иметь место на нулевой частоте, как показано на рис. 1.3-1,6, или на некоторой промежуточной частоте или частотах, как 1[Оказано на рис. 1.3v- 1,в-д. Такое отклонение ил

Более общий термин по отношению к широко истюльзуемым КОИ (конвертор отрицательного (импеданса) полного сопротивления) и КОС (конвертор отрицательного сопротивления). Однако, ниже мы будем использовать сокращение КОИ. - Прим. пер.

пульсация часто определяется на уровне - 3 дБ, хотя могут быть выбраны и другие величины. Амплитудно-частотные характеристи-/ ки, для которых все локальные максимумы и минимумы в задан/ ном диапазоне частот имеют одинаковую величину в полосе пру'-пускания, как показано на рис. 1.3-1,г и д, называются равнр-волновыми. Характеристики, значение производной от которых не меняет знак в заданном диапазоне частот, называются монотт-ными. Например, такова характеристика, приведенная на шс. 1.3-1,6. Другой пример - характеристики, показанные на рис. 1.3- 1,6 и г; их можно описать как равноволновые в полосе пропускания и монотонные за ее пределами. Все нули функций пени нижних частот, амплитуды которых показаны на рис. 1.3 - 1,р-г, должны в общем случае лежать в бесконечности. Следовательно, полиномы в числителе этих функций должны быть нулевой йтепе-ни, т. е. числитель должен быть постоянной величиной, независимо от степени полинома в знаменателе. В общем виде это можно записать так:

iV(s)=:Я/B(s), (1)

где Я не является функцией s, а вид полинома B{s) зависит от элементов заданной цепи. Например, для цепи на рис. 1.1-2 B{s)=s+2s+2s+\. i

Амплитудно-частотная характеристика ФНЧ при нулево1 частоте обращается в ненулевую положительную величину. Следовательно, фазочастотная характеристика (ФЧХ) всех ФНЧ, функции цепи для которых имеют вид, определяемый выражением (1), начинается с нуля (в предположении, что Я>0) и убывает при возрастании частоты. Если функция цепи является рациональной, то максимальное значение фазы равно -90 п° на бесконечно большой частоте; здесь п - порядок полинома в знаменателе B{s). Таким образом, максимальное значение фазы для фильтра, показанного на рис. 1.1-2, равно -270°.

Если характеристика равноволновая как в полосе пропускания, так и в полосе задерживания, занимающей диапазон частот .ш<оо, то происходит модификация основной АЧХ ФНЧ, как показано на рис. 1.3-\,д. Такая характеристика называется эл-. липтической, причем амплитуда на бесконечно большой частоте может быть равна нулю или (как показано) быть ненулевой. Чтобы характеристика была эллиптической, нули функции цепи должны лежать на оси jco плоскости комплексной частоты. Следовательно, эллиптические функции цепи имеют вид

N{s)A{s)IBi,s), (2)

где нули A(s) лежат на оси jco, а нули B{s) -в левой полуплоскости.

В отечествениой литературе чаще используют термин неравномерность АЧХ (для аналоговых фильтров); термин пульсация используется обычио в цифровых фильтрах. Этот термин, как более адекватный, используется и здесь. - Прим. пер.

Следующий тип фильтра, который рассмотрим в этом парагра-г, - фильтр верхних частот (ФВЧ). Фильтр верхних частот за-рживает нижние частоты (полоса задерживания) и пропускает зхние частоты (полоса пропускания). Некоторые АЧХ для

жций цепи верхних частот показаны на рис. 1.3-2. Их описа-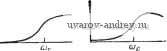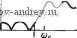

б) - ej

Рис. 1.3-2. Вид основных АЧХ ФВЧ

ние амалогично сделанному в случае ФНЧ. На рис. 1.3-2,а показана идеальная (нереализуемая) характеристика, на рис. 1.3- -2,6-4 полностью монотонная характеристика. На рис. 1.3-2,в и г даны характеристики, равноволновые в полосе пропускания и монотонные вне ее, а на рис. 1.3-2,д - характеристика, равновол-новая как в полосе пропускания, так и в полосе задерживания 0<fl№s, т. е. эллиптическая. В этом случае на нулевой частоте амплитуда может быть равна нулю или (как показано) быть ненулевой. Для ФВЧ ширина полосы пропускания бесконечно велика, так как теоретически она простирается до бесконечно больших частот. Поэтому вместо того, чтобы определять ширину полосы, было бы более разумно определить частоту среза, которая на рисунке обозначена как ©с. Все нули функции цепи верхних частот, АЧХ которых показаны на рис. 1.3-2,а-г, должны в общем случае лежать в начале координат плоскости комплексной частоты. Следовательно, для рациональных функций они должны иметь вид

N{s) = H/B{sj), (3)

где Я - постоянная, а п - степень полинома знаменателя B{s).

Например, для ФВЧ, схема которого показана на рис. 1.3-3, функция цепи имеет вид

П {s)i\\ is)0,5 sV{s + 2s + 2s+\). (4)

Фазочастотная характеристика для рациональной функции цепи верхних частот, заданной в виде (3), начинается со значения 4-90 п° при нулевой частоте и уменьшается до нуля на бесконечно большой ча- - стоте.

Третий общий тип фильтра, который +

удем здесь рассматривать, - полосовой

фильтр (ПФ). Полосовой фильтр пропу-

екает одну полосу частот (полоса пропу- <кания), тогда как две других полосы ча-

стот а именно, ниже и выше полосы про-

пускания задерживаются (полосы задер- значения элементов даны кивания). Некоторые АЧХ-41увкЦВИ-цени----£1 омах, генри, фарадах