причем сумма кратностей полюсов равна степени знаменателя Q{p) передаточной функции W{p), т. е.

то импульсная характеристика определяется более сложной формулой:

v=o u?=o P

p=Pv fi

(2.41)

Предположим теперь, что входной величиной линейной части системы является скачкообразная функция (см. рис. 2.5, б)

(1 при >0,

W-() = {o при .<0. (2-42)

Реакцию линейной части системы на воздействие вида скачкообразной функции будем называть переходной характеристикой. Изображение скачкообразной функции равно

Yip) = L{l{f)} = j. (2.43)

Следовательно, из (2.31) находим изображение переходной характеристики

Z{p)==Hip)=. (2.44)

Обозначим переходную характеристику через h{t). Поскольку деление на р в области изображений соответствует интегрированию в области оригиналов, то из (2.41) получаем

/ W .-S .V iiel ,2.45)

О v=o м,=0 v=0 х=0

где для краткости обозначено

Если полюсы W (р) простые и отличные от нуля, то s = п, Го = г,= ... =г„=1, fx = 0, и из (2.45) и (2.46) получаем

Л(0 = Соо+]с„оеЧ (2.47)

где

Р{0) Р (ру) ,

Если W{p) имеет все простые полюсы и один из них равен нулю, т. е. S = п - 1, Го = 2, /-, == /-2 = ... = = 1, то из (2.45) и (2.46) следует:

h (t) = Coo + Cot + S ce -, (2.49)

где

Coo -

P{p)

dp L Q (P)

P(0)

Q(0)

в тех случаях, когда W{p) представляет собой отношение трансцендентных функций, формулы разложения при некоторых ограничениях сохраняют свой вид, но число полюсов становится равным бесконечности.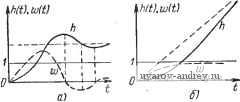

Рнс. 2.6. Примерный вид временных характеристик: а) -устойчивая, б) -нейтральная линейная часть. Сплошные кривые соответствуют переходным характеристикам, а жирные пунктирные линии-нмпул сным характеристикам.

Переходная характеристика является функцией времени и вид ее может быть самым разнообразным в зависимости от параметров и структуры линейной части системы. На рис. 2.6, g и б изображен примерный вид временных характеристик для устойчивой (а) и нейтральной (б) линейных частей системы. Импульсные характеристики представляют собой производные переходных характеристик. Они изображены жирными пунктирными линиями на рис. 2.6, а и б.

Частотные характеристики. Предположим теперь, что ко входу линейной части системы приложено гармоническое воздействие (рис. 2.5,б), которое мы будем обозначать через y{t),

y{t) = y{t)y cosiat + ), (2.51)

где ут, ш и г]) - амплитуда, частота и фаза и которое представляет собой вещественную часть более общего воздействия, записанного в комплексной форме:

Здесь

г/(О == Уте'

Ут<

(2.52) (2.53)

- величина, определяющая амплитуду и фазу гармонического воздействия, называемая комплексной амплитудой.

Так как изображение y{t) равно

y{p)-L{y{t)}=j, . (2.54)

то изображение выходной величины Z(p) найдется умножением Y{p) на передаточную функцию W{p), т.е.

Z{p) = W{p)j- (2.55)

.Кроме полюсов передаточной функции W{p), изображение Z{p) имеет еще один полюс, р = /ы. Воспользовавшись общей формулой разложения*), выходную величину в этом случае можно представить в виде

z{t) = W(;ш)е' +ут е'\ (2.56)

v=0 ц=0

где

l--{p-.pj . (2.57)

1 d V

(Av-H-l)I dp-v-- LQ(p)(p-/cu)

Выражение (2.56) состоит из двух составляющих. Первая составляющая представляет собой периодическую функцию времени и характеризует вынужденный процесс в линейной части системы. Обозначим этот. периодический или в данном случае гармонический процесс через z{t). Вторая составляющая выражения (2.56) характеризует переходный процесс в линейной части системы. Характер этого переходного процесса зависит от полюсов pv передаточной функции W{p). Если эти полюсы pv имеют отрицательные вещественные части, то вторая составляющая выражения (2.56) с ростом веремени t стремится к нулю, и в системе будет существовать вынужденный или, в данном случае, установившийся процесс

() = W7(/co)Le , (2.58)

или, принимая во внимание (2.52),

t{t) = W{{t)- (2.59)

Величина 1(/ш), связывающая гармонически изменяющуюся входную величину y{t) с установившейся, также гармонически

*) См. Приложение I.

изменяющейся, выходной величиной z(t), называется частотной характеристикой. Сопоставляя передаточную функцию W{p) с частотной характеристикой К^(/сй), замечаем, что последнюю можно рассматривать как частный случай передаточной функции при р - /ш.

Таким образом, для получения частотной характеристики следует в передаточной функции W{p) заменить р на /ш. Для пояснения физического смысла частотной хаарктеристики представим ее в показательной форме:

й7(/(о) = И7о(©)е'б( , (2.60)

где К^о (с) - модуль, а е(ш)-фаза. Тогда выходную величину линейной части системы в установившемся режиме можно согласно (2.58), (2.59) и (2.53) представить в виде

г it) - Го (со) yei м+Ф). (2.61)

Отсюда следует, что частотная характеристика показывает, как изменяются амплитуда Wo(a)ym. и фаза е(ш) + г]) выходной величины линейной части системы при изменении частоты входной величины.

В вещественной форме выражение для установившейся выходной величины линейной части можно представить в виде

g(0 = Wo(M)t/cos(©/-f е(со) + г1)). (2.62)

Отсюда вытекает известное правило определения установившегося режима при гармоническом воздействии.

Для определения установившегося режима при гармоническом воздействии необходимо амплитуду последнего ут умножить на Wo (о), а к сдвигу фаз г]; прибавить е(ш), где ш -частота внешнего воздействия.

Зависимость Wo{a) от ш называется обычно амплитудно-частотной характеристикой, а зависимость е(ш) от © - фазо-частотной характеристикой.

Для целей дальнейшего исследования удобным оказывается представление частотной характеристики в виде суммы вещественной и мнимой частей

W (/со) = {/(©) + jV (со). (2.63)

Воспользовавшись известным равенством

g/e cos е (со) + / sin 6 (со),

нетрудно из (2.60) найти выражение для вещественной и мнимой частей:

C/(cu) = iro(to)cose(ai), F (со) = Wo (а) sine (а). (2.64)

Задаваясь различными значениями со, можно построить амплитудно-частотную и фазо-частотную характеристики (рис. 2.7, й) либо вещественную и мнимую части (рис. 2.7,6) частотной характеристики.

Часто эти характеристики совмещают и изображают частотную характеристику W(/co) в комплексной плоскости {U, jV), или, что то же самое, в полярной системе координат {Wo, 6). На рис. 2.7, е изображен примерный вид частотной характеристики устойчивой линейной части (кривая /), соответствующей р^нее изображенным характеристикам Uo(co), G(co) и t/(co), К(со), а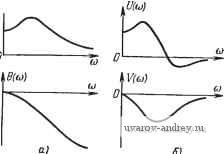

Рис. 2.7. Амплигудно-частотная и фазо-частогная характеристики {а), действительная и мнимая части частотной характеристики (б), амплитудно-фазовые характеристики (е): /-для устойчивой, 2-для нейтральной линейной части. \

также примерный вид частотной характеристики нейтральной линейной части системы (кривая 2). Иногда предпочитают изображать частотную характеристику в логарифмической прямоугольной системе координат (201g Uo(co), 6(со)).

Частотные и временные характеристики тесно связаны между собой. Известны соотношения, позволяющие по частотным характеристикам вычислить временные и обратно.

Так, если линейная часть системы устойчива, т. е. W (р) имеет все полюсы с отрицательными действительными частями, то импульсная характеристика w{t) определяется формулами

w{t)-- и ((d) cos at da

(2.65)

или

w{t) =--V (<o) sin со/ dco.

(2.66)

Аналогично может быть определена и переходная характеристика h{i) формулами:

sin at da

или

- cos at da.

h{t)=U{0) +

Соотношения, обратные к (2.65) -(2.68), имеют вид

U{a) = h{0)+ { w{t)cosatdt

(2.67)

(2.68)

(2.69)

причем

V{a)= w (t) sin at dt,

w{t) = h{t).

(2.70),

(2.71)

В том случае, когда линейная часть нейтральна и W{p) имеет один полюс, равный нулю, а действительные части остальных полюсов отрицательны, формулы (2.65) и (2.66) заменяются на

tc;(/) = f/(0) +

cos at da

или

(0 = t/(0) + 4

cos at da.

(2.72) (2.73)

a формулы (2.67) и (2.68) - на

hit)V{0) + U{0)t + j

или

h{t)U{0)t + -

U(0)-U (ffl)

cos(oM(o (2.74)

(2.75)

в качестве обратных соотношений к (2.72) - (2.75) теперь будем иметь

о

W (t) sin at dt, (2.76)

V (ш) = - -i- j w(t) cos at dt, (2.77)

где

w{t) = h(t). (2.78)

Приведенные выше соотношения являются простыми следствиями основных определений прямого и обратного преобразований Лапласа при р = /со; они справедливы и в том случае, когда W{p)-трансцендентная функция, т.е. для элементов с распределенными параметрами.

Для практического применения этих соотношений обычно аппроксимируют и (а), V(a) (если нужно найти w(t)) или w{t), w{t) (если нужно найти U{a) или V(a)) отрезками прямых, для которых вычисление содержащихся в формулах интегралов не представляет труда.

Благодаря этому вычисление импульсной w{t) или переходной h{t) характеристик по формулам (2.65), (2.66) или (2.67), (2.68) не требует предварительного определения полюсов передаточной функции W{p), знание которых необходимо при вычислении временной характеристики по формулам разложения. Это обстоятельство особенно важно в тех случаях, когда линейная часть сложна, содержит внутренние, обратные связи, элементы с распределенными параметрами и т. д., т. е. тогда, когда полюсы W{p) не могут быть просто определены через параметры элементов.

Методика приближенного определения w{t) или h(t) по U{a) или V{a), а также U(a) и V{a) по w{t) или h{t) довольно подробно описана в литературе по линейной теории автоматического регулирования*).

В заключение заметим, что по w{t), и W{ja), по крайней мере принципиально, можно найти реакцию линейной части системы на воздействие любого вида.

§ 2.3. Уравнения релейных элементов

При отсутствии гистерезиса уравнение релейного элемента Можно представить в виде существенно нелинейной зависимости

У = Ф{х), (2.79)

*) См. В. В. С о л о д о в н и к о в [1], А. А. Воронов [1], [2].

где

Ф (х) = kp sign X =

К О

при X > о, при х = 0, при X < О,

(2.80)

при отсутствии зоны нечувствительности (см. рис. 1.48, е) и

- [sign {х - Ко) + sign {х + щ)] =

I -k

р при X > Хо, при х|<Ио, при Х<-Ио,

(2.81)

когда имеется зона нечувствительности (см. рис. 1.48,(5).

При наличии гистерезиса уравнение релейного элемента не может быть записано в виде, подобном (2.79), поскольку управляющее воздействие у теперь не однозначно определяется значением управляющего сигнала х.

В общем случае уравнение гистерезисного элемента определяется не функцией от управляющего сигнала х, а оператором; определенном на управляющих сигналах х, и может быть представлено в виде

y(t) = Q){x{f)f,o\ (2.82)

Эта запись показывает, что управляющее воздействие y{t) в момент времени t определяется значением управляющего сигнала x{t) не только в момент времени t, но и его значениями во все предыдущие моменты времени и, кроме того, y{t) зависит от некоторого параметра а*). Для релейных элементов без гистерезиса уравнение (2.82), естественно, упрощается.

Рассмотрим вначале релейный элемент с положительным гистерезисом без зоны нечувствительности (см. рис. 1.48, й). Обозначим через а - У\ = +kp значение управляющего воздействия после последнего переключения реле; тогда уравнение релейного элемента с положительным гистерезисом можно представить в виде

yit) = 0{x; у^), (2.83)

где

Ф (х; Уд =

- kr, для

х>щ,

X < - о,

- Ко < JC < Ио,

если с~у1== kp,

если о = у1 = - kp

(2.84)

*) Задачам описания нелинейных элементов при наличии гистерезиса в общем случае посвящены работы В. А. Якубовича [1], [2] и М. А. К р а с-нрсельскогс [11.

Для описания релейного элемента с отрицательным гистерезисом без зоны нечувствительности (см. рис. 1.48, ж) обозначим а = = signi = ±l- Тогда уравнение такого релейного элемента можно записать в форме:

где

ф(л:; signx) ==

у = ф{х; signx), kp для I

(2.85)

kp для

(2.86)

Х>Ко,

Яох> - Ко,

- щ^х<щ, если 0 = sign х ~ - 1.

Аналогичным образом могут быть записаны уравнения релейного элемента и при наличии зоны нечувствительности. В табл. 2.1 приведены уравнения для типовых релейных элементов с симметричными характеристиками.

Для релейных элементов с гистерезисом величина

Ф{хЦ); a)dx{t)

характеризует приращение площади.

Нетрудно проверить, что характеристики релейных элементов с зоной нечувствительности и гистерезисом удовлетворяют неравенствам

0{x{t); a)dx{t)kp\xit) \,

(2.87)

где а~у1 - dtkp или О, если гистерезис положителен, и

Ф(х(0; a)dxit)-kp\x{0)\,

(2.88)

где а = sign л: = ±1, если гистерезис отрицателен*). Таким образом, уравнение релейного элемента с гистерезисом мы будем записывать в форме

у = Ф{х;а). (2.89)

Здесь а = у1, где уи равное ± или О - значение управляющего воздействия после последнего переключения, если гистерезис положителен, и а = sign л: = ±1, если гистерезис отрицателен.

*) Неравенство (2.88) является частным случаем условия положительности В. А. Якубовича [1], [2].

ТАБЛИЦА 2.1

Характеристики и уравнения типовых релейных элементов

у=Ф(х. о)

kp х>0, -kp х<0.

у = Ф^{х,а) =

X >>{(

щ^х> - щ,

а = J/I = kp.

\ -Кв<:Х<У

<Хо,

а = у1 = - kp.

а X

у = Ф^(х, а) =

Х>Хо,

Ко>х> - Хо,

а = signA: = 1.

< - Но,

ио<х<х;о,

<Т= sign X = -1,.

У

у = Ф^{х) =

kp Х> Хо,

о -щ<х<щ, - kp л; < - о-