где

Pi (0) Qi(0)

Pi(Pv) Ql(Pv)Pv

(14.23)

После подстановки й в (14.11) получаем

n-l n-l + 4 CvoCpO

2c2 - f

W-1 n / n-l /

. (14.24)

Зная 6(0, находим z{t), используя уравнение второй линейной части,

2(0=2 5Д0

(14.25)

где - реакция на начальные условия, - полюсы переда точной функции 12 (р) (для простоты они предполагаются простыми), и, наконец.

fi= 1, 2, .... п.

(14.26)

Начальные условия определяются требованием периодич Hocrti:

После преобразований имеем *)

2я , . 2я

- 2с2 -

2п

е - 1 - 9ц

V, Г1=1

ш

fl-l

2п

9ц - Pv

1+е

2л

е - е - Wfi-Pv) -е

V (О

9ц

9ц - Рц - Рг]

V, Г1=1

-2с^1

401 Ьп-

Cvi е ~е

---ЙГ +

l-l. Pv -

, , Cv

(9ц - Pv)

. (14.27)

Дифференцируя это соотношение по /, получим e{t):

ч2 р W

Чсо/ п-1

9ц

2п

2п

V, п=1

) См. Ю. в, Д о л г о л е н к о [6].

2л

fп--I

e - e

2л

e - e - (9ц - Pv) - e

(9u - Pv)

,2 u

Zji q - Pv -

qe* - (Pv + Pt) e

( v+Pr,)

V, 11=1

Pv - Pn

(1 + Л^)(,+Л^)

/ Cvo

, X vo 9n le - e V j (1, p.,) p.y/e v

2л

(14.28)

Соотношения (14.27) и (14.28) определяют выходную величину разомкнутой экстремальной системы и ее производную. Выше

предполагается, что z (/) непрерывно при О < , т. е. что

z(t) при не имеет скачка, что обычно выполняется в

экстремальных системах с инерционным объектом. В идеализированном случае, соответствующем безынерционному объекту, следует учитывать скачки 2 (/). Учет их производится обычным путем. Мы, однако, этот случай далее рассматривать не будем.

§ 14.3. Условия существования периодических режимов

Рассматривая поведение координат разомкнутой экстремальной релейной системы при периодическом воздействии (см. рис. 14.6), нетрудно установить условия существования периодических режимов в виде условия надлежащего момента переключений

(14.29)

и условия надлежащего направления переключения.

(~)<0- (14.2.9,1

Кроме того, должно быть выполнено условие отсутствия дополнительных переключений, которое состоит в том, что не существует таких значений t (О / 2зт/сй), для которых выполняются одновременно условия

xit) = - Ko, Jc{t)<0. (14.30)

В общем случае здесь

x(0 = 5(0 + Лfo(coo;-f Ф), (14.31)

а при отсутствии внешнего воздействия (Л = 0)

x(t)z{t). (14.32)

В последнем случае условия существования автоколебаний (14.29) и (14.29) запишутся в виде

12я\

<0.

2п

(14.33)

Этим условиям можно дать удобную геометрическую интерпретацию на основе понятия годографа релейной экстремальной системы.

§ 14.4. Годограф релейной экстремальной системы

В отличие от годографа обычной релейной системы, определим годограф релейной экстремальной системы как

/ (ш) = Re / (ш) + Лт / (ш) = I () + }z [). (14.34)

Полагая в (14.20), (14.21) t =

находим

2 оо W

(2т- 1)

п=1 т~1

2т - I

X {102 [( - т) ш] cos [е, [{2п - 1) -f)

-W7o2[( + /n-l)o)]X

-e,((2m-l)f )-f е2(( -т)со)

>< cos [e, ((2n - I) I-) -f e, ((2m - 1) -) -f 02 ((n + m- 1) -f)] }

. (14.35)

X { 02 [( - т) со] (п - т) sin [б, ((2п - 1) -) - е, ((п - т) --) +

+ б2((и--т)со) - - 1Го2 [( + m - 1)(й](п -f m - 1) sin [б, ((2 - 1)-) +

+ е, ({2т - + 62 ((я -f m - I) со)] }. (14.36)

Поскольку в релейной экстремальной системе с инерционным объектом z{t) непрерывна, выражение годографа релейной экстремальной системы можно представить в виде

оо оо

п=1 т=\

(2 -1)-

(2 -1)-

2 - 1

2т- 1

(2 -1)

(2.г-1)--

п=1 т=1

2 ~ 1

2m-l

X { 20 (( - т) со) [(п - т) sin [б, ((2п - 1) - - е, ((2т - 1) --) + 62 (( - т) со)] - / cos[e, [{2п - 1) --) -- е, ((2т - 1) -)-Ь 62 (( - т) со)] -- W2o[in + m - 1) со] [(п + m - 1) sin [б, ((2п - 1) -) -f + 6, ((2m - 1) -f-) + 62 ((n + m - 1) )] - / cos [е, ((2/г - 1) -) -Ь + e, ((2m - U-f) + Ы(п -f m - l)co)] ] }. (14.37)

Можно получить выражение годографа релейной экстремальной системы не в виде ряда, а в замкнутой форме. Для этого нужно воспользоваться соотношениями (14.27) и (14.28). Полагая в них t = 2я/со, будем иметь

(1=1

2л

/ at

9 2 ]

V. 11=1

2n , 2эт

-2cl

- 1 - 9й

n-l

01 (0

2n 2л

2л

2ЭТ -

e - e - (9ц - Pv) - e

..2 -I

2n,

\2e ~\

2Я 1 m

(14.38)

+ 2-X

9ц

/2л , л

(0 ?i (0; + 2 9ц-ру-р^

V, rj=l 2Л

9ц IT (Pv+Pri) S в с

-1-9ц

2я со

2л

4 > со 2 9,-

2л

2л

9ц-Pv

2п

1+е

- е - (9ц - Pv) - е

2п

2я PvlT

1+е

2л

2л ц и

е

2Я й (О

0,1 -Pv -

2 / 2л

24 />-

-2- е 9ц \

I* со

CvoCtio 9це -(Pv + PTi)e

ч 2Л

( v+Pii) IT

, 9ц-Pv-Pn ( piU pHN

> (О

2л

2л

(9ц - Pv)

/ 2л 2л\ 2л

2л

(14.39)

Часто при анализе релейных экстремальных систем можно рассматривать приближенное выражение для годографа /(со), которое значительно упрощает вычисления.

Если ограничиться в (14.37) слагаемыми при п = m = 1, то

Ji)w![i)wAO)e-+Wi{j)wAi<). (14.40)

Учитывая, что W2{0) = 0, получаем

Ч )--Г?(/-2-)Г2(/(0).

(14.41)

Это выражение с точностью до постоянного множителя совпадает с эквивалентной частотной характеристикой экстремальной системы, которая широко используется при анализе экстремальных систем на основе приближенного метода гармонической линеаризации *).

§ 14.5. Исследование периодических режимов

Введенное выше понятие годографа релейной экстремальной системы позволяет исследовать периодические режимы (автоколебания и вынужденные колебания) в экстремальных системах таким же путем, как и в обычных релейных автоматических системах. Действительно, согласно определению годографа (14.34) условия существования автоколебаний (14.33) можно записать в виде

Im/((u)== -Хо, 1

I (14.42)

Re/(cu)<0.

*) Эквивалентная частотная характеристика экстремальной системы введена И. С. МоросаноБым [1].

Эти условия имеют обычную геометрическую интерпретацию. Проведем на плоскости годографа релейной экстремальной системы прямую -Хо (рис. 14.7). Точки пересечения годографа /((о) с этой прямой, лежащие в левой полуплоскости, и определяют возможные частоты автоколебаний. Исследование автоколебаний проводится по методике, описанной в главах V, VI.

При наличии внешнего периодического воздействия частоты (Оо величина x{t) определяется соотношением (14.31). Условия

j/mjiol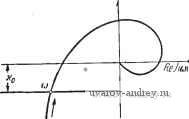

Рис. 14.7. Годограф релейной экстремальной системы. К определению периодических режимов.

Рис. 14.8. Определение условий существования вынужденных колебаний релейной экстремальной системы по годографу / (и).

(14.29), (14.29) существования вынужденных колебаний интерпретируются при помощи коплекснозначной функции, которая аналогична введенной в § 8.1:

(2я - ф) = Л [fо' (2я - ф) + /7о (2я - ф)]. (14.43)

Строя эту комплексиозначную функцию относительно точки (О = СОо годографа релейной экстремальной системы /(со), определяем при заданной амплитуде фазовые сдвиги ф (рис. 14.8), которые соответствуют возможным вынужденным режимам. Аналогичным образом, заменяя (14.43) на

(2я - ф) = Л [ vf; (я - ф) -f /7о (2я - ф)] (14.44)

при заданном v, можно исследовать и возможные субгармонические режимы (см. § 8.5). Таким образом, исследование существования периодических и, в частности, субгармонических режимов в релейных экстремальных системах, по существу, ничем не отличается от методики исследования периодических режимов в обычных релейных системах. Это дает возможность довольно просто решать задачу коррекции релейных экстремальных систем.

Исследование устойчивости периодических режимов в релейных экстремальных системах сводится к исследованию устойчивости соответствующей нелинейной импульсной системы. Нелинейность вызвана наличием в релейной экстремальной системе параболического звена. Хотя принципиально задача исследования устойчивости возможных периодических режимов и разрешима, мы ее из-за сложности здесь рассматривать не будем.

§ 14.6. О сложных периодических режимах

В некоторых типах экстремальных регуляторов, работающих по отклонению от экстремума, используются нелинейные элементы с несколькими порогами срабатывания, кратными величине Хо (рис. 14.9). В таких релейных экстремальных системах могут возникать так называемые сложные периодические процессы, которые характеризуются тем, что выходная координата объекта z{t) пересекает -

и---т -

более одного уровня квантования.

Рис. 14.9. Нелинейный элемент с несколькими порогами срабатывания.

Рис. 14.10. Условия существования сложного периодического режима.

Будем называть сложным периодическим режимом кратности Л' такой периодический режим, когда выходной сигнал объекта пересекает N уровней квантования. На рис. 14.10 показаны процессы в релейной экстремальной системе, когда в ней возникает сложный периодический режим. Из этих графиков видно, что сложный периодический режим связан с повышением потерь на поиск.

Условия существования сложного периодического режима естественным образом вытекают из рис. 14.10. Для режима кратности N они имеют такой вид

. s=l, 2, iV, (14.45)

{Q < 0.

Сложный режим i/jv(0 можно представить*) в виде суммы простых режимов, смещенных на время 4 == (-1) ~*УбГ, где Г -период сложного периодического процесса z(t)

(0=2У7-( + (-1ГЧаГ), 8 = 0,1,2, N, (14.46) -1 Y, = 0.

Здесь г(;+(-l)ysT)-простой периодический процесс с периодом Т, смещенный на время {-l)ysT.

Воздействие jv(0 поступает на вход линейной части с передаточной функцией Wi{p) и, следовательно, ее выходную величину можно представить в виде

uAt)=urit + {-iy~ysT), (14.47)

где через йг(; + (-О^ув) обозначена реакция линейной части на элементарное периодическое воздействие yrit + {-l)~\sT). Согласно структурной схеме системы (14.11) и рис. 14.4 имеем

vAt)= Iiurit + {-iy\sT)ur{t + {-lY-yj), (14.48)

S=l r=il

М

zAt)= liSr,m{t), (14.49)

где .

Из этих соотнощений следует, что для вычисления выходной величины объекта в сложном периодическом режиме можно использовать ранее полученные выражения для простых периодических режимов (14.20) и (14.21), если ввести семейство годографов релейной экстремальной системы, определяющих сложные режимы:

JNi)-S,() + jz,(f). (14.51)

Используя эти годографы, условия существования сложного периодического режима можио записать в виде

Im /д, (со) = - 8щ,

Re/ (co)<0. =1>2,...,;V. (14.52)

Эти условия подобны условиям существования сложных режимов в обычных релейных автоматических системах (см. § 5.5).

*) См. Ю. С- П о п к о в [1].