Составим уравнение

f/n(co)+F ( ))+- = 0.

(13.21)

левая часть которого совпадает с левой частью неравенств (13.17), (13.17). Уравнение (13.21) представляет собой в плоскости Wn прямую Попова, проходящую через точку (--у-, oj

с наклоном -1. Поэтому критерий устойчивости частотно-импульсной системы, вытекающий из неравенств (13,17) и (13.17)., можно сформулировать в следующей форме:

Частотно-импульсная автоматическая система будет устойчива в целом, если общая линейная часть системы устойчива

Рнс. 13.10. К формулировке критерия устойчивости в целом частотно-импульсной системы.

Рис. 13.11. К формулировке критерия устойчивости в целом частотно-импульсной системы (при 9=0).

или нейтральна, а преобразованная частотная характеристика линейной части Un(/co) лежит справа от прямой Попова для значений со, при которых (Ji{a) > О, и лежит слева от прямой Попова для значений со, при которых {Ji{m) < О (рис. 13.10) *). . В частном случае для И-частотно-импульсной модуляции

Ki{jm) = - e-actgT, > (13,22)

fi/cD -f I /rfcB + I

Следовательно,

-tg6,(co) = rico и f/,(co)>0. (13.23)

При этом вместо двух условий (13.17) и (13.17) получаем одно условие:

(/ ( ) +Г,соК„(со)+> О,

(13.24)

*) Критерий устойчивости в этой форме был установлен В. И. Д ы м к о-вым [1].

так как г = kiJT\. Действительная и мнимая части преобразованной характеристики (13.20) в этом случае равны

Кп(сй) = Г,(0Ун(( ). J

Частотно-импульсная автоматическая система будет устойчива в целом, если общая линейная часть устойчива или нейтральна, а преобразованная частотная характеристика линейной части 1п(/со) располагается справа от прямой Попова, проходящей

через точку, (--, с наклоном -1 (рис. 13.11). Попытка

применить этот частотный критерий устойчивости для обычной частотно-импульсной модуляции не приводит к конструктивным результатам. Действительно, в этом случае

ii(/co) = = r. . (13.24)

Следовательно,

f/i( )) = 0, l/i((o) = -<0, (13.25)

и значит, из условия (13.16) получаем

F (ft)) = lmir (/a))>0. (13.26)

Очевидно, что для реальных систем это условие не может быть выполнено, так как оно соответствует опережающим, нереализуемым устройствам. Причина такой ситуации состоит в том, что мы насильно в критерии устойчивости приняли = 0. Таким образом, для систем с частотно-импульсной модуляцией следует пользоваться общим критерием устойчивости, сформулированным в § 13.3 *).

§ 13.5. О периодических режимах

В частотно-импульсных системах, как и в иных нелинейных системах, при невыполнении условий устойчивости в целом возможно возникновение автоколебаний. Эти автоколебания могут быть подавлены внешним периодическим воздействием, которое навязывает системе вынужденные колебания. Описанные в предыдущих главах методы исследования периодических режимов пригодны и для частотно-импульсных систем. Периодический

*) См. А. X. Гелиг [6-8].

7£

Рнс. 13.12. Сложный периодический режим.

вежим В частотно-импульсных системах в общем случае соответствует сложному периодическому режиму, так как в полупериодах возможно различное число импульсов управляющего воздействия (рис. 13.12). Поэтому решение задачи о периодическом режиме с произвольным числом импульсов в полупериоде сводится к исследованию сложных видов периодических режимов. Лишь тогда, когда чи-ело импульсов в полупериоде равно единице, мы приходим к исследованию простейших видов периодических режимов.

Эти же замечания можно сделать и по отношению к вынужденным колебаниям. При фактическом вычислении годографов частотно-импульсной автоматической системы, по которым определяются периодические режимы, следует учитывать специфику общей линейной части. Передаточная функция и частотная характеристика общей'линейной части определяются выражениями (13.5) и (13.9), причем, индекс всегда равен единице. Устойчивость возможных периодических режимов исследуется с помощью уравнений в вариациях, методика составления которых остается без существенных изменений. Мы не будем выписывать выражений годографов частотно-импульсной системы и ее уравнений в вариациях и проводить исследования периодических режимов, так как при необходимости это может быть сделано читателем по аналогии с обычными релейными системами.

В заключение отметим, что процессы в устойчивых частотно-импульсных системах представляют собой реакцию линейной части на конечное число импульсов, постоянных по амплитуде и длительности. Поэтому построение процессов сводится к суммированию реакций линейной части на смещенные друг относительно друга импульсы. Это обстоятельство позволяет несколько упростить построение процессов. Но методика построения процессов остается аналогичной той, которая была описана в главе 1П.

Глава XIV

РЕЛЕЙНЫЕ ЭКСТРЕМАЛЬНЫЕ АВТОМАТИЧЕСКИЕ

СИСТЕМЫ

§ I4.I. Структурная схема

Экстремальная автоматическая система характеризуется тем, что она поддерживает не заданное, а экстремальное - максимальное или минимальное значение регулируемой величины с помощью процесса поиска.

В релейной экстремальной автоматической системе, представляющей собой один из видов экстремальных автоматических систем, управляющее воздействие постоянно по абсолютной величине и изменяет знак на обратный после прохождения экстремума в соответствии с тем или иным правилом переключения. Поиск экстремума в релейных экстремальных автоматических системах осуществляется за счет автоколебаний.

РЭР

Рис. 14.1. Структурная схема релейной зкстремальной автоматической системы.

Рис. 14,2. Характеристика иелинейной части.

Структурная схема релейной экстремальной автоматической системы иображена на рис. 14.1. Регулируемый объект состоит из линейных частей, обладающих передаточными функциями и Ki{p)- Между ними находится нелинейная часть, характеристика которой имеет экстремум. Уравнение нелинейной части запишем в виде

v = F{u\ (14.1)

Обычно при исследовании релейных экстремальных систем предполагается, что эта нелинейная зависимость описывается квадратичной параболой (рис. 14.2). Исполнительное устрой-

ство (ИУ) содержит в себе интегрирующий элемент и, следовательно', его передаточная функция, в частности, имеет вид

/Сиу(р) = -. (14.2)

Выходная величина объекта подается в устройство, вычисляющее показатель экстремума - ту величину, по которой переключается направление поиска. Это устройство - измеритель показателя экстремума - описывается передаточной функцией Квв{р), обычно обладающей свойством /Спэ(О) = 0.

Экстремальный регулятор в рассматриваемой системе переключает направления поиска тогда, когда сигнал на выходе измерителя показателя экстремума переходит заданный порог ±>со. Его характеристика изображена на рис. 14.3, а для случая, когда экстремум - максимум; при этом порог равен -щ.

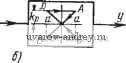Рнс. 14.3. Характеристика экстремального регулятора -(а) и эквивалентная характеристика-(б).

Обозначим множество значений x{t), при которых сохраняется предыдущее значение y(t) через Ах, а множество значений x{t), при которых происходит переключение - через Вх.

Ax[x{t)>-Ko, х(/)<0; x{t)<Ko, x{t)0;

x{t)<-Xo, x{t)0; x{Jt)>-Ko, *(/)>0}, (14.3)

В,[х{{) = -щ, x{f)<Q}. (14.4)

Тогда уравнение характеристики, показанной на рис. 14.3, а, примет вид:

y{t-G) = kp, x(t)< y{t-0) = -kp, x{t) y{t-0)-kp, x{t) y{t-0) = kp, x{t)

Нелинейная характеристика экстремального регулятора, изображенная на рис. 14.3, а, может быть реализована на различных элементах.

Когда впервые появились экстремальные регуляторы этого Типа, они были выполнены на электромеханических элементах. В простейшем из них *) двухпозиционное реле с порогом -ко

y{t) =

при

kp при

Ах, В,.

(14.6)

*) См. Д рей пер и Ли [I].

перемещало рычаг храпового механизма, петлевая характеристика которого изображена на рис. 14.3, б. Последовательное соединение нелинейных элементов, показанных на этом рисунке, может быть описано гистерезисной характеристикой (14.3) - (14.5). Действительно, допустим, что входной сигнал экстремального регулятора х > -щ и начальное положение на характеристике храпового механизма соответствует точке А. При этом выходной сигнал у регулятора равен +ftp. В момент времени ti, когда x{ti)<CO и x{ti) =-ио, выходная величина релейного элемента меняет знак и происходит переход из точки А в точку В. На выходе экстремального регулятора появляется сигнал у = -ftp.

Если x{t) будет теперь возрастать и достигнет при t = t2 величины -Ко, то сигнал на выходе релейного элемента снова изменит знак. Согласно характеристике храпового механизма произойдет переход из точки В в точку С, но при этом сигнал на выходе регулятора сохранится: у = -ftp.

Только теле того как снова окажется л:(з)<0, и x{ts) = - -Хо, произойдет перемещение в точку D, т. е. на выходе регулятора сигнал станет равным -fftp.

Совершенно аналогичная картина имеет место для характеристики экстремального регулятора, изображенного на рис. 14.3, а.

Выходной сигнал y{t) релейного экстремального регулятора представляет собой последовательность импульсов, знаки которых чередуются с частотой вдвое меньшей, чем частота входного сигнала z{t). Переключение реле наступает, когда значение показателя экстремума равно -хо, если экстремум - максимум, и Хо - если экстремум - минимум. При этом условия переключения для экстремума - максимума имеют вид

x{t) = - Ko, x{t)<0, (14.6)

а для экстремума ~ минимума

xit) = Ко, xit)>0. (14.7)

Далее для определенности мы будем полагать, что экстремум есть максимум, а не минимум.

Объединяя линейные звенья, получим расчетную модель релейной экстремальной автоматической системы, изображенную на рис. 14.4. На этой схеме указано возможное внешнее воздействие f{t) и приняты следующие обозначения:

WAp) = -KAp), W2{p)=K2(p)Kns{p). (14.8)

Рабочим режимом релейной экстремальной автоматической системы является режим автоколебаний, который в рассматри-

ваемой системе обладает некоторыми особенностями. Одна из них состоит в том, что процессы v{t), z{t) и x{t) изменяются периодически с частотой со, а процессы y{t) и u{t) изменяются

так же периодически, но с частотой --. В нелинейной части

объекта, характеризуемой функцией F{u), происходит удвоение частоты, так как F{u) -четная функция.

РЭР

Рис. 14.4. Расчетная модель релейной экстремальной автоматической системы.

Другая особенность рабочего режима релейной экстремальной системы состоит в том, что процесс на выходе нелинейной части v{t), а иногда и на выходе объекта z{t), имеет постоянную составляющую, тогда как процесс y{t) ее не содержит, и его форма от величины постоянной составляющей процесса z{t) не зависит.

§ 14.2. Поведение разомкнутой релейной экстремальной системы при периодическом воздействии

Составим прежде всего уравнение релейной экстремальной системы (см. рис. 14.4). Уравнения линейных частей относительно изображений записываются в обычной форме:

U(p) = Wdp)Y{p), Z{p)W,{p)V[p).

(14.9) (14.10)

Уравнение нелинейной части объекта принимается в виде параболы

v{t) = ~ku(t). (14.11)

Что же касается уравнения регулятора, то в общем случае его можно представить в форме

y{t) = Rix{t). Хо. kp).

где Хо, ftp -параметры регулятора, причем

x{t)zit)-i-f{t).

(14.12) (14.13)

Уравнения (14.11), (14.13) относительно изображений записы-ваются в виде

V{p) = -kL{uHt)}. (14.14)

и

: Y(p) = L{R{xit). щ, kp)}. (14.15)

Разомкнем экстремальную систему на входе регулятора (рис. 14.5) и подадим на вход этой разомкнутой системы периодическое воздействие частоты со.

Хотя в реальной системе процесс x{t) имеет постоянную составляющую, но, как отмечалось выще, на вид процесса y{i) на выходе экстремального регулятора она не влияет. Поэтому при подаче на вход регулятора только периодической компоненты форма процесса y{t) будет та же, что и в реальной замкнутой системе.

Характеризменения величин в различных точках разомкнутой экстремальной системы изображен на рис. 14.6. Здесь наглядно видно удвоение частоты и независимость величин между выходом экстремального регулятора и входом квадратичного нелинейного элемента от постоянной составляющей. Найдем периодически изменяющиеся величины z{t) и z{t) разомкнутой экстремальной системы. Это можно сделать двумя путями. Первый путь основан на использовании частотных характеристик.

Представим периодическую знакопеременную последовательность частоты сй/2 в виде ряда Фурье. Для этой цели заменим Б (5.12) со на ю/2:

() = S; (2 -1)T-- (14.16)

Тогда, замечая, что частотные характеристики линейных частей равны

1Г,(Усо) = 1Г,о( ))е'е.( , 1Г2(/сй) = 1Г2о(ю)е№(о)), (14.17)

находим реакцию выходной величины первой линейной части в виде

(2т-1)

= -7Г S 2т-1 [( - 1) f + е, ((2т -1) -1-)

(14.18)

РЭР

f(u)

Рис. 14.5. Разомкнутая экстремальная система.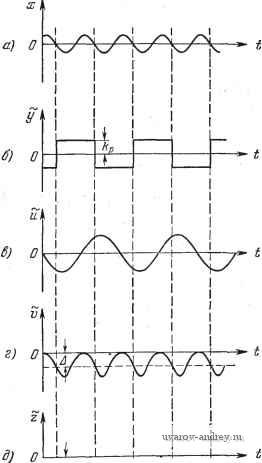

Рис. 14.6. Характер изменения величин в разомкнутой релейной SKcrpeMaJlbHoa системе.

Подставляя u{t) в (14.П), получим

-8/efec

(2 -l)f

2n- I

2m- 1

Xcos[(n-m)co< + e,((2n-l)-)-e,((2m-l)-) -- cos [(n + m-1) со; + e, ((2n - 1) --) + 6, ((2m - . (14.19)

Зная t)(;), легко найти z(t) обычным путем

5(0 = -

n=l m=l

(2 -I)-

2n - I

2/n- I

х{2о[(п- m) ш] cos [{n -m)cit~ 6, ((2n - 1) -f-) -e, ((2m - + 02 (( - m) co) -- №'20 [( + m - 1) со] cos ( + m - 1) co + + 6, ({2n - 1) --) e. ((2m - 1) f) + e2(( -m) со)] }. .(14.20) Дифференцируя (14.20) по t, получим

Ht)-

8kkp

(2m-Df

(2/n-I)-

2n-l

2m- I

X { 120 [( - m) со] (n - m) sin [( - m) + G, ((2 - 1) -e,((2m-l)--)-fe2((n-m)co) -- 2o\in + m- 1)ш](я + m - 1) sin ( + m - 1)ш; +

+ 9, ((2 - 1) f) + e, ((2m - 1)--) + 62 (( + m - 1) ш)]}. (14.21)

Второй путь основан на представлении реакции линейных частей экстремальной системы в замкнутой форме, которая аналогична приведенным в §§ 11.3, 11.4. Поскольку первая линейная часть в релейной экстремальной системе, как правило, содержит интегратор, то реакция этой линейной части представ-.ляется в виде

u{t)= - kp

<:14.22}