Оригиналы, соответствующие этим изображениям, равны

t

Следовательно, условие существования непрерывного скользящего режима (12.26) примет вид

или, так как е <1, то

10 <. (12.29)

Таким образом, если величина внешнего воздействия не превосходит величины йрГаб/Гс, то будет иметь место непрерывный скользящий режим.

Условие (12.29) можно получить и не определяя оригиналов Zi(t) и Xi(t). Поскольку они достигают своих максимальных значений при = О, то достаточно определить Zi{Q) и i(0) и подставить их в неравенство (12.26) при = 0. Найти i(0) и х(0) можно с помощью теоремы о предельных значениях.

Действительно, согласно теореме 8 о предельных значениях (Приложение 1)

г, (0) = lim р

kp kp

л;,(0)= hm р т^бр+Л ~ТЖ-

р~>оо

Подставляя эти значения в (12.26) при = О, приходим к найденному выше условию существования непрерывного скользящего режима (12:29).

При отсутствии гистерезиса скользящий режим соответствует движению с бесконечно большой частотой включений и бесконечно малой амплитудой изменений x{t). Поэтому его часто называют идеальным скользящим режимом *).

*) Иные подходы к определению условий существования скользящих режимов в релейных системах описаны Ю. В. Долголенко [3], Ю. И. Н е й-марком [5], [6], П. В. Бромбергом [3], а в более общих разрывных системах В. И. У т к и н ы м [1], [2].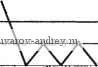

Учет гистерезиса делает частоту включений и амплитуду конечными. Так, для релейной системы с характеристикой релейного элемента с зоной нечув-* ствительности, изображенной

на рис. 12.10, g, характер изменения x(t) будет иметь вид, показанный на рис. 12.18. Та-t кое движение соответствует - - реальному скользящему режиму. При и- -О или ?t-*l этот реальный скользящий режим переходит в предельный. Ре-

Рис. 12.18. к пояснению реального сколь- ИЛЬНЫЙ СКОЛЬЗЯЩИЙ рСЖИМ, ПО зящего режима. СуЩССТВу, ЯВЛЯСТСЯ рабоЧИМ

режимом частотно-импульсных автоматических систем, которым посвящена глава XIII.

§ 12.5. Сопоставление способов линеаризации

Описанные в предыдущих параграфах способы линеаризации релейных систем могут быть реализованы лишь при выполнении соответствующих условий, которые были выше рассмотрены.

Важное значение при выборе частоты и амплитуды дополнительного периодического воздействия имеет понятие годографа релейной системы /(со), применяющееся при исследовании автоколебаний и вынужденных колебаний. С помощью годографа /(со) можно определить критические значения амплитуд дополнительного воздействия (при превышении которых в системе будут существовать вынужденные колебания основной частоты или субгармонические колебания, обеспечивающие линеаризацию релейной системы), а также выяснить влияние параметров тех или иных внутренних связей на частоту автоколебаний (в тех случаях, когда линеаризация производится за счет автоколебаний).

По годографу релейной системы /(со) можно также установить необходимое условие существования скользящего режима. Это необходимое условие будет выполнено, если годограф релейной системы /(со) не пересекает действительной оси в левой части плоскости и индекс линейной части равен 1.

Очевидно, что вынужденные колебания или автоколебания, линеаризующие систему, должны быть устойчивыми, а также должно быть устойчивым положение равновесия релейной системы, линеаризуемой при помощи скользящего режима.

Считая, что все эти условия выполнены и, следовательно, релейная система линеаризована, произведем краткое сопоставление рассмотренных способов линеаризации.

Линеаризация релейной системы при помощи вынужденных колебаний позволяет в широких пределах изменять частоту и амплитуду дополнительного периодического воздействия и тем самым осуществить необходимую линеаризацию. Изменением амплитуды дополнительного периодического воздействия можно изменять коэффициент усиления системы. Если эту амплитуду сделать зависимой от некоторой величины, характеризующей состояние системы, то вместе с изменением последней будет изменяться и коэффициент усиления.

При линеаризации этим способом линейная часть системы остается неизменной.

Линеаризация релейной системы при помощи автоколебаний ограничена в возможности изменения частоты и амплитуды автоколебаний. Если все же удается достигнуть линеаризации, то тем самым влияние параметров элементов линейной части, охваченных обратной связью, устраняется. Однако это обычно справедливо при относительно медленном изменении внешнего воздействия.

Отметим, что оба эти способа линеаризации позволяют эффективно устранять влияние зазоров, люфтов, сухого трения и т. д. *) и пригодны для релейных систем с любым видом характеристик релейных элементов, в том числе и тех, для которых коэффициент возврата отрицательный.

При линеаризации с помощью скользящего режима устраняется влияние параметров исполнительного устройства, охваченного обратной связью.

Все описанные способы характеризуются тем, что верхний предел скорости изменения внешнего воздействия ограничен. Кроме того, средняя скорость выходной величины исполнительного устройства всегда меньше ее скорости при длительном включении, т.е. при отсутствии линеаризации.

Если линеаризация релейной системы тем или иным способом осуществлена, то процесс, протекающий в ней, определяется соответствующей линеаризованной системой. Схемы этих линеаризованных систем для соответствующих способов линеаризации были приведены в предыдущих параграфах.

Расчет линеаризованных систем в диапазоне их линейности ничем не отличается от расчета линейных систем непрерывного регулирования. Он достаточно подробно изложен в литературе по теории автоматического регулирования, к которой мы и отсылаем читателя.

*) Об этом см., например, А. А. Красовский [1], В. А. Бесекер-с к и й [1]. . f 1- F

Глава XIII

ЧАСТОТНО ИМПУЛЬСНЫЕ АВТОМАТИЧЕСКИЕ

СИСТЕМЫ

§ 13.1. Понятие о частотно-импульсных автоматических системах

Частотно-импульсные автоматические системы характеризуются тем, что управляющее воздействие представляет собой последовательность импульсов постоянной амплитуды и длительности, модулированных по частоте (рис. 13.1). С одной стороны,

эти системы представляют собой существенно нелинейные импульсные автоматические системы, а с другой стороны, многие из них можно рассматривать как разновидности релейных автоматических систем, работающих в скользящем режиме. Это последнее обстоятельство позволяет использовать результаты теории релейных автоматических систем для анализа и исследования частотно-импульсных систем.

Частотно-импульсные автоматические системы широко применяются в различных областях техники. Примеры некоторых частотно-импульсных автоматических систем были приведены в главе П. В последние годы интерес к исследованию процессов в частотно-импульсных системах возрос в связи с тем, что подобные же процессы имеют место при передаче информации в нервной системе живых существ, в формальных моделях нейронов и нейронных сетях.

Мы не будем здесь останавливаться на классификации частотно-импульсных автоматических систем и специфических методах их исследования. Интересующиеся этим кругом вопросов могут обратиться к специальной литературе*).

*) См. В. М. Кунцевич, Ю Н Чеховой [3]. В этой монографии приведена библиография работ по частотно-импульсным системам. Из последних работ укажем работы Кана и Джури [1], А. X. Г ели г а [4-81. .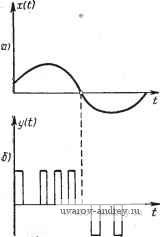

Рис. 13.1. Управляющий сигнал 10) и управляющее воздейс вие б) в частотио-импульсной автоматической системе.

Ограничимся рассмотрением частотно-импульсных систем, которые приводятся к эквивалентньш релейным автоматическим системам.

§ 13.2. Представление частотно-импульсной системы в виде релейной автоматической системы

Структурная схема частотно-импульсной автоматической системы изображена на рис. 13.2. Она состоит из частотно-импульсного модулятора и непрерывной линейной части. Частотно-импульсный модулятор преоб-

ЧИН

Wjp)

2ft)

Рис.- 13.2. Структурная схема частотно-импульсной системы.

разует непрерывный управляющий сигнал x{t) в последовательность прямоугольных импульсов постоянной амплитуды, расстояние между которыми зависит от величины управляющего сигнала. Это значит, что частотно-импульсный модулятор осуществляет модуляцию частоты следования импульсов.

Во многих случаях подобный частотно-импульсный модулятор (рис. 13.3) можно представить в виде следящей релейной

чин

xit),

и, (pi

yit)

Kcip)

Рис. 13.3. Частотно-импульсный модулятор (а) н эквивалентная ему релейная автоматическая система (б).

системы, работающей в скользящем режиме с конечной частотой скольжения (см. § 12.4). Эта релейная система состоит из релейного элемента с характеристикой Ф, имеющей гистерезис и, вообще говоря, зону нечувствительности, и двух линейных элементов (рис. 13.3,6). Передаточные функции К.\{р) и /Сс(р) этих элементов должны быть таковы, чтобы выполнялись условия скользящего режима. Типичная характеристика релейного элемента, применяемая в ряде частотно-импульсных модуляторов, изображена на рис. 13.4. Для нее хо > О и О < X < 1 (с), либо Хо > О и X = О (б). Из условий существования скользящего режима (см. § 12.4) следует, что индекс / передаточной функции Ki(p)Kcip) должен быть равен единице.

Конкретный выбор передаточных функций Ki{p) и Кс{р) определяет вид частотнр-импульсной модуляции. Так,

передаточная функция

(13.1)

соответствует обычной частотно-импульсной модуляции, а

(13.2)

соответствует так называемой 2-частотно-импульсной модуляции.

-Кр -ЛКо

/.Но Hq

Рис. 13-4. Характеристики релейного элемента в частотно-импульсных модуляторак и > 0: О < Ж 1 (а) Ка>0. Я=0 (б).

Передаточная функция Кс{р) при этом не должна зависеть от р и обычно она равна

(13.3)

Ко(р) =

где

г = lim pKi (Р) = k, (0) ф 0.

(13.4)

Заметим, что для обычной частотно-импульсной модуляции

г = ki, & для Е-частотиой импульсной модуляции г = -. Если

обозначить длительность модулируемых импульсов через Тп и выбрать

~ То

то площадь импульсов будет единичной. При То->-0 коэффициент fep -* оо и выходная последовательность импульсов частотно-импульсного модулятора будет представлять собой последовательность модулированных по частоте следования импульсов бесконечно малой длительности, бесконечно большой амплитудь! и

конечной площади, которые описываются импульсивными функциями.

Пользуясь эквивалентным представлением частотно-импульсного модулятора в виде простейшей релейной системы с гистерезисом, можно частотно-импульсную автоматическую систему изобразить в виде релейной автоматической системы с внутренней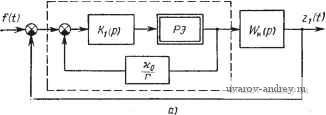

f(t)

<2)-*.

WapJ

Рис. 13.5. Релейная авгоматическая система с внутренней обратной связью, эквивалентная частотно-импульсной системе, а) -исходный вид, б)-преобразованный внд.

обратной СВЯЗЬЮ (рис. 13.5,а). Эта система может быть приведена к эквивалентной форме (рис. 13.5,6) при надлежащем пересчете внешнего воздействия f{t). Таким образом, частотно-импульсная система представляет собой некую релейную систему

Рис. 13.6. Простейшая форма релейной автоматической системы.

С внутренней обратной связью, предназначенной для создания скользящего режима.

Объединяя линейные элементы и линейную часть в общую линейную часть, получим схему эквивалентной релейной системы в привычной форме (рис. 13.6).

. Передаточная функция общей линейной части этой релейной системы равна

W{p) = [wAp) + ~]KdP)- (13.5)

К полученной релейной автоматической системе применимы описанные выше методы исследования.

§ 13.3. Критерий устойчивости в целом

Для устойчивых в целом частотно-импульсных систем число импульсов, появляющихся на выходе релейного элемента, конечно, т.е. после некоторого момента времени на выходе релейного элемента импульсы возникать не будут.

Исследование устойчивости в целом частотно-импульсной

-Г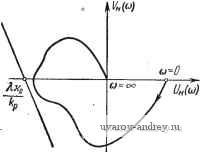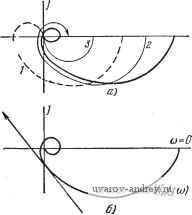

Рис. 13.7. К формулировке критерия устойчивости в целом частотио-импульсной автоматической системы, Кфо.

Рнс. 13.8. Построение модифицированной частотной характеристики линейной части.

системы можно провести на основе частотного критерия устойчивости релейной автоматической системы, установленного в § 4.6. Сформулируем этот критерий устойчивости применительно к рассматриваемым частотно-импульсным системам.

Для того чтобы частотно-импульсная система была устойчива в целом, достаточно, чтобы общая линейная часть системы была устойчива или нейтральна, а частотная характеристика общей линейной части системы удовлетворяла условию

Re (1+9/ ))1Г (/( ) +

Ли о

(13.6)

где 90.

Введем обозначение для модифицированной общей частотной характеристики

й?м(/ )) = /м((о) + уТЛ )), (13.7)

где

f/ (co) = f/((o)-Reir(/G)), 1 F (со) = ©F (й) = ю Im W(/<й). /

(13.8)

Используя результаты, изложенные в § 4.6, приходим к такой формулировке критерия устойчивости в целом для частотно-импульсной системы.

Частотно-импульсная автоматическая система будет устойчива в целом, если модифицированная частотная характеристика ее общей линейной части лежит справа от прямой Попова,

проходящей через точку-- и имеющей неположительный

наклон (рис. 13.7).

Так как общая частотная характеристика линейной части, получаемая из (13.5) при р = /со, равна

W(/(o)= WAh) + (/< ).

(13.9)

то модифицированную общую частотную характеристику можно построить по частотной характеристике линейной части следующим образом (рис. 13.8). На плоскости W изображаем частотную характеристику Wnijai) = Uaia)-\-jVh{(a) (кривая 1), смещаем ее вправо на величину (кривая 2) и перемножаем с частотной характеристикой /(i (/со) (кривая 3). Тем самым находим W(/co) (рис. 13.8, с). Изменяя каждую ординату частотной характеристики общей линейной системы в <й раз, получаем модифицированную частотную характеристику общей линейной части 1Fm(/co) (рис. 13.8,6). Проводя прямую Попова с неположительным наклоном, определяем конкретные параметры, при которых частотно-импульсная автоматическая система устойчива в целом. В частности, для систем с обычной частотно-импульсной модуляцией

откуда следует, что

(/ (со) = V (со) = Im (/со),

Vu (со) = - [f/н(00) + 1 1 - - kyU, (со) - щ,

(13.10)

(13.11)

так как г == ki.

Модифицированная частотная характеристика может быть построена согласно (13.11) непосредственно по действительной И мни!иой частям Ц7н(/со).

§ 13.4. Частные случаи

Рассмотрим некоторые частные случаи частотного критерия устойчивости в целом для частотно-импульсной системы. При Я = О или = оо из (13.6) получаем

Re(l+9/й))Г(/(о)>0.

В этом случае прямая Попова проходит через начало координат (рис. 13.9). Придадим теперь параметру q фиксированное

значение, а именно, положим 9 = 0. Тогда из (13.10) получаем

Reir(/(o)>0 или, с учетом (13.9),

(13.13)

Wh(/co) + JK,(/ ))>0.

(13.14)

Поскольку

W (/co) = f/H ( )) + /r (co),

Рис. 13.9. к формулировке критерия устойчивости в целом частотно-импульсной автоматической системы при Я=0.

/Ci(/co) = (/,(co) + yT,( )). то условие (13.14) представится в виде

иЛ) + f/i( ))-F ( ))F,( ,)>0.

(13.15)

(13.16)

После деления на <7, (со) ф О имеем

иЛ)-1Т^)Л<>)-\->0, если C/i( ))>0 (13.17)

или

1Л<)-1Т^)Л^) + < если f/,(co)<0. (13.170 Замечая, что

-ftS==tge,(co), (13.18)

где 01 (со) -фазовая характеристика линейного элемента, обладающего частотной характеристикой Ki(/m), введем преобразованную частотную характеристику 1}п(/со)

где

Wn<yco) = t/n(co) + /F (o)), (13.19)

г Л (13-20)

t/n( ))=t/ (co) = RerH(/co), F (со) = - tg 6 (со) У„(со) = - tg 6 (со) Im W,