Глава XII

ЛИНЕАРИЗАЦИЯ РЕЛЕЙНЫХ АВТОМАТИЧЕСКИХ

§ I2.I. Физические основы линеаризации релейного элемента

Релейный элемент является существенно нелинейным элементом. Выходная величина релейного элемента (управляющее воздействие) изменяется скачком, когда входная величина (управляющий сигнал) проходит пороговые значения. В интервале между моментами времени, соответствующими прохождению входной величиной пороговых значений, выходная величина релейного элемента неизменна.

Такие свойства релейного элемента позволяют сравнительно простыми средствами коммутировать большие мощности, но пропорциональность между выходной и входной величинами здесь отсутствует.

Если одновременно с управляющим сигналом на вход релейного элемента подавать дополнительное периодическое воздействие, то релейный элемент может при определенных условиях приобрести свойства пропорциональности.

Для выяснения этого эффекта предположим вначале, что релейный элемент не обладает зоной нечувствительности и дополнительное периодическое воздействие .Лfд((oO таково, что

f[<(t+i-)] = -fA<i)- (12.1)

Здесь, как и ранее, принято, что тах| fa((o/) = 1.

Выходная величина релейного элемента при наличии дополнительного воздействия Лfд((oO и сигнала Xi{t) будет равна

y(t) = 0[xi(t) + Af,{cot)]. (12.2)

Предположим пока, что Xi (t) представляет собой постоянную величину Хи, тогда

Аргумент этой нелинейной функции

Хп + А!,{Ш}

при условии

I I < А

периодически изменяет знак. Поэтому yit) =y{t) представляет xit) собой также периодическую функ-

цию с частотой дополнительного периодического воздействия.

Это наглядно иллюстрируется рис. 12.1, где изображены входная и выходная величины релейного элемента при различных значениях х^. Так как y{t) = - yit) представляет собой пе-. риодическую функцию, то ее можно представить в виде ряда Фурье: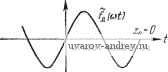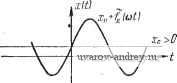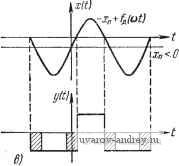

y{t) = \-VyCrZo{t-\(,).

(12.4)

Каждому значению Хп будут соответствовать своя величина постоянной составляющей, а также величина амплитуд и фаз гармоник. Постоянная составляющая определяет среднее значение y{t). Обозначим последнее через г/ср. Тогда

г/ср = -у-.

(12.5)

Если на выход релейного элемента включен фильтр нижних частот, который ослабляет все гармоники, то выходная величина фильтра как раз будет равна г/ср-Найдем зависимость г/ср от х-ц. Среднее значение равно алгебраической сумме площадей импульсов с положительным и отрицательным знаками, отнесен-

в) x < 0. 2л;

п нон к периоду -.

Как видно из рис. 12.1,6, разность площадей будет равна где определяется как абсцисса, при которой функция Л/д((оО

Рнс. I2.I. Определение зависимости от Xj, при а) JC[,=0. б) > О,

достигает значения, равного Хи, т. е. является наименьшим корнем уравнения

Лfд((DДO = л:п. (12.6)

Обозначая через f функцию, обратную функции fд, находим значение Д^ в виде

=if:(-)- . (12-7)

Следовательно, искомое среднее значение уср будет равно

Это выражение справедливо при \хи\ <. А. Если же \Хи\ А, то переключений реле не происходит и

t/cpl = V (12.9)

Из (12.8) следует, что среднее значение выходной величины

релейного элемента определяется функцией от обратной

к функции дополнительного воздействия.

Чтобы найти зависимость г/ср от достаточно по заданной

функции внешнего воздействия /д((оО в интервале - ш*

построить ей обратную функцию, используя обычный графический прием зеркального отображения относительно биссектрисы, проходящей через I к III квадранты, с учетом масштабов по осям.

Построенные таким образом зависимости г/ср от Хи Для различных форм дополнительного воздействия приведены в табл. 12.1 *).

Нетрудно видеть, что эта зависимость имеет тот же характер, что и зависимость фазы вынужденных колебаний от амплитуды дополнительного воздействия, которая была приведена в

табл. 8.1 (стр. 301). Предположим, что f~( ) непрерывна в окрестности начала координат. Обозначая через к/ наклон касательной к f~ при Хп = О, эту функцию при малых значениях - можно заменить линейной функцией ш тогда

*) См. Г. С. Поспелов [1]-[3].

Уср

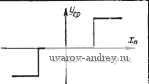Если дополнительное воздействие имеет форму треугольника (табл. 12.1), то последнее выражение справедливо во всем диапазоне изменения -j- от -I до Полученные выше соотношения (12.10) или общая форма (12.8), очевидно, остаются справедливыми, если сигнал Х\ будет не постоянной, а переменной величиной, медленно изменяющейся по сравнению с ffl(co/) (рис. 12.2). В этом случае

Чкр , / X, (О

(12.11)

Зависимость Уср от Хп для различных форм дополнительного воздействия А7д(а)0

XI it)

при \xi{t)\< л или при малых значениях

Уср it)

. X, (t)

(12.12)

Таким образом, при наличии дополнительного периодического воздействия относительно высокой частоты по сравнению с входной величиной {управляющим сигналом) релейный элемент {вместе с фильтром) превращается в функциональный преобразователь. Закон преобразования опреде-1 ляется функцией, обратной к функ-

ции дополнительного периодического воздействия.

xit)

Xn-AfJcjt)

Рис. 12.2. к пояснению пропорциональной зависимости у^ от х it).

Рис. 12.3. Опрелелсние зависимости у^ от прн ЩФО; Х=1.

В частном случае при дополнительном воздействии треугольной формы релейный элемент превращается в линейный усилитель с коэффициентом усиления

2fepfef пА

Коэффициент усиления такого линеаризованного релейного элемента обратно пропорционален амплитуде А внешнего периодического воздействия.

Рассмотрим теперь релейный элемент с зоной нечувствительности.

Для выходной величины этого релейного элемента, как видно из рис. 12.3, разность площадей равна

2/Sp(A,-fA/2).

где Ai и Д<2 являются наименьшими (по абсолютной величине) корнями уравнений

Л?д(сйД<,) = п-Ио. Л^д(сйД^2)=Хп + Хо> (12.13)

соответственно.

Отсюда находим, что

I .-1 / а:о - Ир \ д, , I .-1(Хп + аЛ

где fд' - функция, обратная к f

Среднее значение г/ср в этом случае будет равно

2fep (Ml + As) 2я л

,-.() + ,;(i4-)]. (,2.14,

Для того чтобы найти ср. нужно, как это следует из (12.14), сместить /д (-1 вдоль оси абсцисс на величины ±

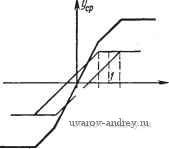Рис. 12.4. Зависимости j/j,p от-- при ЯсьО и =1; а) -дополнительное воздействие синусоидальной формы, б) дополнительное воздействие треугольной формы.

(рис. 12.4, а) и полученные таким образом кривые сложить. Изменяя теперь масштаб вдоль оси ординат в - раз, находим

зависимость Уср от Эта зависимость симметрична относительно начала координат, а при \ Хп\> А + щ становится постоянной.

При %Q = 0 из (12.14) получаем прел<ний результат (12.8).

Для малых значений из (12.14) будем иметь

А

Xyi Kg Л^п Ч~ (

лп - /VQ лп -г ло 2р ЛГп г. гч

где fef - наклон касательных к f (-х^) точках Хп = ± о-Это же выражение будет справедливо в диапазоне изменений Хп от -Л + /о до А-Ио, если дополнительное воздействие имеет треугольную форму, как это видно из построения рис. 12.4,6.

В рассмотренных случаях зона нечувствительности не оказывает влияния на среднее значение выходной величины г/ср, которое в некотором диапазоне линейно зависит от входной величины. Таким образом, при линеаризации влияние зоны нечувствительности устраняется.

Наличие гистерезиса (что соответствует отличию Х от 1) не изменяет полученных выводов. Заметим, что если амплитуду А, а также коэффициенты релейного элемента fep, kq сделать медленно меняющимися функциями времени, то релейный элемент вместе с фильтром можно рассматривать как некоторое вычислительное устройство, осуществляющее операции вычитания, деления и нелинейного преобразования.

Таким образом, подача на вход релейного элемента дополнительного высокочастотного периодического воздействия наряду с медленно изменяющейся по сравнению с ним входной величиной {управляющим сигналом) приводит, по крайней мере

при малых изменениях J , к линеаризации релейного элемента, т. е. к тому, что среднее значение выходной величины его становится пропорциональным величине Xi{t) (см. рис. 12.4). При этих условиях релейный элемент эквивалентен линейному усилителю. Характерной особенностью такого усилителя является зависимость коэффициента усиления от амплитуды внещнего воздействия А. Увеличение последней уменьшает коэффициент усиления.

В общем случае релейный элемент эквивалентен нелинейному усилителю (функциональному преобразователю). Это позволяет использовать подобный элемент в адаптивных системах.

Если в релейной системе создать высокочастотные (по сравнению с внешним воздействием) колебания, то релейная система приобретает свойства линейной или пропорциональной системы, причем настройка этой последней системы может осуществляться за счет изменения амплитуды этих относительно высокочастотных колебаний. Роль фильтра в релейной системе будет играть ее линейная часть.

Дополнительное высокочастотное воздействие, осуществляющее линеаризацию релейной системы, может быть создано при помощи вынужденных колебаний или автоколебаний, если эти колебания существуют и устойчивы.

Процесс линеаризации аналогичен процессу модуляции. Релейный элемент представляет собой модулятор, дополнительное периодическое воздействие соответствует несущей частоте, а внешнее воздействие (управляющий сигнал)-модулирующему сигналу.

Более точно в релейном элементе при наличии дополнительного периодического воздействия происходит своеобразная ши-ротно-импульсная модуляция. Отсюда вытекает соотношение между частотой модулирующего сигнала и несущей, при кото рой процесс модуляции будет осуществлен без существенных искажений. Отношение частоты несущей к частоте сигнала должно быть по крайней мере больше трех*). Это накладывает ограничения на скорость изменения управляющего сигнала.

Несколько цной способ осуществления линеаризации связан с созданием так называемого скользящего режима, о котором речь будет далее.

Рассмотрим подробнее эти способы линеаризации релейных систем.

§ 12.2. Линеаризация вынужденными колебаниями

Рассмотрим релейную систему автоматического регулирования (рис. 12.5). В общем случае в ней, если не приняты соответствующие предосторожности, будут автоколебания некоторой частоты (Оо- Если к релейной системе приложить дополнительное периодическое воздействие частоты со, создаваемое некоторым генератором, то прн превышении амплитудой этих колебаний критического значения, определяемого, например, по годографу релейной системы /(о) (см. § 8.1), автоколебания частоты юо будут подавлены, но вместо них возникнут вынужденные колебания частоты Ир. Если эти вынужденные колебания устойчивы, то, выбирая частоту со значительно большей соо, мы не только устраняем автоколебания, но и линеаризуем релейную систему. При достаточно высокой частоте cOq линейная часть системы сильно подавляет гармоники y{t), начиная с сОд, и тогда выходная величина z(t) будет зависеть (с точностью до подавления этих гармоник) от среднего значения управляющего воздействия г/ср, которое при отсутствии внешнего воздействия равно нулю. Если к системе приложено внешнее воздействие f{t).

*) См., например, Л. А. Меерович и Л. Г. Зеличенко [1],

Генератор

1}Ч

т

медленно изменяющееся по сравнению с частотой вынужденных колебаний, то релейная система будет реагировать на него как некоторая линеаризованная или нелинейная непрерывная система автоматического регулирования (см. рис. 12.5,6).

Эффект подавления автоколебаний и линеаризацию релейных систем указанным способом называют вибрационной линеаризацией. Примерами релейных систем, линеаризованных вынужденными колебаниями, могут служить описанные в § 1.1 простейшая релейная следящая система (см. рис. 1.24), в которой дополнительное периодическое воздействие подается иа первичную обмотку трансформатора; следящая система с управлением по скорости (рис. 1.27), в которой дополнительное периодическое воздействие подается на специальные обмотки реле. В этих системах дополнительное периодическое воздействие создается независимым генератором. Обычно частота этого генератора выбирается в пределах 10-50 гц.

Отметим, что принципиально место подачи дополнительного периодического воздействия безразлично.

Однако для уменьшения мощности независимого генератора целесообразно дополнительное периодическое воздействие подавать на вход измерительного устройства или релейного элемента, обладающего малым потреблением мощности.

Некоторым неудобством описанных выше систем является необходимость в наличии отдельного независимого генератора. Это неудобство устранено в системе автоматического регулирования числа оборотов (см. рис. 1.13), где роль генератора дополнительных периодических колебаний играет сама регулируемая величина. Благодаря кулачку, связанному с валом центробежного тахометра, контакты 5-5 находятся в непрерывном колебательном движении, что эквивалентно наличию дополнительного периодического воздействия. То обстоятельство, что в этой системе частота колебаний контактов несколько изменяется вместе с изменением регулируемой величины, не играет существенной роли, если эта частота относительно велика.

Линеаризация релейных систем автоматического регулирования вынужденными колебаниями обладает гибкостью в смысле

Рис. 12.0. Линеаризация релейной автоматической системы вынужденными колебаниями (а). Схема линеаризованной системы (б).

возможности изменения в широких пределах частоты и амплитуды дополнительного периодического воздействия.

Дополнительное воздействие может быть создано соответствующей схемой самого релейного устройства, если придать ему свойства генератора, т. е. включить по схеме самовозбуждения, например, по типу электрического звонка или электромагнитного прерывателя*), как это показано на рис. 12.6.

Вых -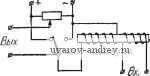

а) 6]

Рне. 12.6. Включение реле по схеме самовозбуждения.

Частота колебаний здесь зависит от электрических и механических постоянных времени. Эти схемы могут быть разнообразными.

Примерами систем, в которых независимый генератор отсутствует, могут служить: следящая система на переменном токе (см. рис. 1.25), в которой благодаря конденсаторам 5-5 осуществлена прерывистая работа тиратронов так, что частота Р2 Р1 импульсов тока в тиратроне

t пропорциональна величине напряжения на сетке; система измерения скорости судна (рис. 1.28), в которой колебания подвижного контакта создаются электромагнитами, работаю-щими по схеме самовозбуждения (электрического звонка).

Весьма интересен с точки зрения совмещения релейного элемента и генератора дополнительного периодического воздействия релейный время-импульсный элемент**). Схема его приведена на рис. 12.7. Релейный время-импульсный элемент

*) Теории подобных электромагнитных прерывателей посвящены работы Н. А. Ф у ф а е Б а [1], [2].

**) Этот элемент предложен А. Б. Челюсткиным [1]. Он был применен и детально исследован в качестве регулятора электрических машин В. Г. В а с и л ь е в ы м. . .

Рис. 12.7. Релейный время-импульсный элемент.