ризации - частотной характеристикой, то автоколебания отсутствуют. В действительности же согласно точному методу (рис. 11.15,6), где использован годограф релейной системы /(и) из табл. 6.4 заключаем, что в системе имеют место автоколебания частоты (Оо, определяемой точкой пересечения прямой

11 UllO)

Vac. U.I5. Применение метода гармонической линеаризации (а). Применение точного

метода (б).

-Хо С годографом /((о). Значения частоты и амплитуды автоколебаний легко определить аналитически. Из условия

1т/((Оо)=-г() = -АоШ2=-хо, где ko - kjkp, находим

С0о==-

Г, 1п

и поскольку

кр + Щ ко - Ко

(11.92) (11.93)

тах2() = ио,

то амплитуда автоколебаний равна ис, т. е. автоколебания происходят внутри петли гистерезиса (рис. 11.16). Причина несоответствия результатов точного и приближенного методов состоит в резкой несинусоидальности автоколебаний.

Метод гармонической линеаризации непосредственно не применим к системам с внутренними обратными связями (рис. 11.17), если индекс передаточной функции Wi (р)

не превышает единицы. Это следует из того, что внутренний контур, охватывающий релейный элемент, ведет себя как рассмотренная выше простейшая релейная автоматическая система.

Рис. п. 16. Вид автоколебаний.

Для иллюстрации этого факта приведем числовой пример Пусть частотная характеристика основной линейной части имеет вид

а частотная характеристика элемента обратной связи равна

На рис. П.18, й изображены частотные характеристики Wo(/co), Wi (/(о) и сумматорная частотная характеристика

* W (/со) = Wo (/со) + Г, (/со), (11.96)

а на рис. П.18, б изображен годограф релейной системы /(ю), полученный суммированием двух годографов, /о (со) и /i(m).

Как видно из рис. 11.19, на котором изображены годограф релейной системы /(м) и частотная характеристика в изменен-

ном масштабе - W (/ю), они существенно отличаются друг от

друга. Можно провести горизонтальную прямую -ио так, что по приближенному методу будут возможны автоколебания частоты а по точному методу - автоколебания частоты много

большей, чем Для иных значений величины щ приближенный метод дает по-прежнему автоколебания лишь одной частоты rajf, а по точному методу - автоколебания частоты ©(j), cojp), afK Таким образом, здесь имеет место не только количественное, но и качественное различие. Можно подумать, что это различие обусловлено свойством импульсной характеристики линейной части: w{0) ф О, для которой левый и правый годографы релейной системы отличны друг от друга. Покажем, что метод гармонической линеаризации может привести к неверным выводам и для релейных систем, в которых w{0) = О, т. е. когда левый и правый годографы совпадают.

Рассмотрим, например, ту же релейную систему с внутренней обратной связью (см. рис. 11.17), но в которой li(/co) (11.95) заменено на

( )-(0.01Д.Н- (11-97)

На рис. 11.20, й приведено построение, соответствующее методу гармонической линеаризации, а на рис. 11.20,6 - соответствующее точному методу. Из сопоставления годографа /( ) и

W (/©) В этом случае следует, что при щ 2 приближенный метод приводит к заключению об отсутствии возможных

Щ(р) -J

Рис. 11.17. Релейная система с внутренней обратной связью.

3,0 Ю

3D 450

jV(u)

Wtjci) 50 УО W Ulu)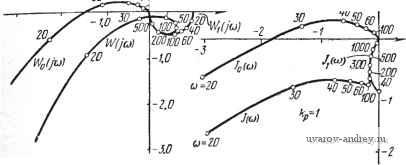

ReJiuj)

r(a)=Jg(u)*J,(a) 6)

Рис. 11.18. Частотные характеристики Wo (/(0), Wx (/и) и (la) + Wi (/ш) -(a); годографы /о (ш), /, (со) и /о ((a) + /, (00) -(б).

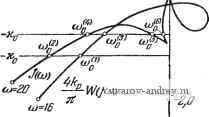4ftp

Рис. 11.19. Сравнение годографа / (и) и частотной.характеристикиIF (О)),

автоколебаний, тогда как согласно точному методу автоколебания могут иметь место при любом щ > 0.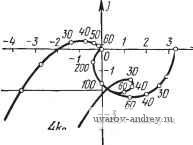

/?eJ(co)

Рис. 11.20. Частотные характеристики Wc (/ш), Wi 0 ш) и IWo (/со) + (а); го-

дографы /о (и), J, (ш) и /. (ш) + / (ш) -(б).

♦

Из приведенного рассмотрения вытекает уточненный приближенный метод исследования автоколебаний в подобных релейных автоматических системах, состоящий в использовании выражения годографа

/ (оз) = /,(со) + -1Го(/со),

в который входит годограф /i(o)) релейной системы, образуемый внутренней обратной связью, и первое слагаемое годографа релейной системы без обратной связи*). На рис. 11.21 приведены графики точного J (а) и приближенного У ((о) годографов релейной системы, которые весьма близки друг к другу.

Рассмотрим еще релейную автоматическую систему, линейная часть которой неустойчива**), а релейный элемент не имеет зоны нечувствительности, но может обладать гистерезисом. Предположим для определенности, что частотная характеристика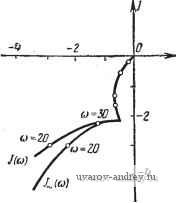

Рис. 11.21. Сравнение годографов / (со)

и (00).

*) См. Н. А. К О р О л е в [3].

На этот пример, внимание автора было обращено Е. К. Круг и о. М. М и н и н о й.

такой системы равна

или

lF(/co) =

jA((a)7-,)2+l)((cor,)+l)

g/(n-l-arctg шГ,-arctg иГг)

Качественный вид частотной характеристики, увеличенной в

раз, т. е. -IF (/со) при Ti > Гг, изображен на рис. 11.22.

Обратному неравенству (Г, < Гг) соответствует характеристика, симметричная относительно действительной оси. В этом случае автоколебания отсутствуют, и поэтому мы ее рассматривать не будем.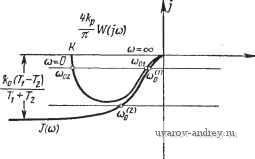

г *,=4

Рис. U.22. К сопоставлению точного-и приближенного метода исследования автоколе-

Пользуясь выражением годографа релейной системы /(со), приведенным в табл. 6.4, полагая в нем Г = -Ту, Т' - Гг и изменяя ко на -ко, получим выражение годографа релейной системы в рассматриваемом случае

/(со)

Ti + T,

2aTi

+ th

-/(r,th-

-To th-

2(oT, 2(07-2 / где ко = л^р-

Качественный вид этого годографа /(со) при Г1 > Гг изображен также на рис. 11.22. Можно показать, что 1т/((о) при (а~*оо стремится к величине

Ко 7-, +

Для определения частоты возможных автоколебаний нужно на плоскости этих характеристик провести прямую -хо. Точки

пересечения этой прямой в левой части плоскости с годографом /(со) определяют значение частоты автоколебаний согласно точному методу, а точки пересечения с кривой -~W(j(i)) - значение частоты автоколебаний согласно приближенному методу. Из рис. 11.22 следует, что при О <щ<. оуру согласно точному

методу имеется всегда одна частота возможных автоколебаний coi при <р = х|, и со<2 при х'К Согласно же приближенному методу при >{q = имеются две частоты возможных автоколебаний cooi и (Й02 (причем, при малых х^ значение cooi близко к со)), а при x = x[f автоколебания отсутствуют. Это сопоставление свидетельствует о сильном качественном различии результатов точного и приближенного методов. Приближенный метод приводит к выводу о существовании частоты автоколебаний соог, которая отсутствует, и об отсутствии частоты автоколебаний со*,, которая существует.

Аналогичные результаты совпадения и расхождения точного и приближенного методов имеют место и при исследовании вынужденных колебаний.

Tow построена по Ли)

---Прибт - wcmpoem по

If WIja]

Рис. 11.23. Сопоставление границ существования вынужденных колебаний в релейной следящей системе, полученных точным (сплошная кривая) и приближенным (пунктир)

методами.

На рис. 11.23 приведено сопоставление границ существования вынужденных колебаний для следящей системы, подробно изученной в предыдущих главах. Как и выше, сплошная линия соответствует точному результату, а пунктирная - приближенному, В этом случае границы существования вынужденных колебаний вблизи частоты автоколебаний качественно и количественно совпадают. Вдали от частоты автоколебаний имеет место количественное расхождение.

Отметим, что это расхождение зависит от точки приложения внешнего воздействия.

Определим границы существования непрерывных вынужденных колебаний в электрическом приводе при учете сухого трения.

Так как f/((o) в этом случае положительно (см. рис. 10.28), то критическое значение амплитуды определяется выражением (11.90). Амплитуда внешнего воздействия, приведенного к входу релейного элемента, равна

Л = двД

(см. § 8.6).

Частотная характеристика линейной части системы равна

/(Ио7 )2 + 1

После подстановки этих значений в (11.90) получаем приближенное (по первой гармонике) условие существования вынужденных колебаний, т. е. непрерывного движения

B>BiKp = - или - ,

Зависимость -.- приведена на рис. 11.24 пунктиром. Здесь же ftp

сплошной линией изображена точная зависимость, полученная в § 8.6. Приближенная и точная зависимость отличаются не только количественно, но и качественно. В области / приближенный метод приводит к выводу об отсутствии вынужденных колебаний, тогда, как согласно точному методу, они существуют. В области 2 приближенный метод приводит к выводу о существовании вынужденных колебаний, тогда как согласно точному методу, они не существуют.

Нетрудно видеть, что по самой своей идее (предположение о близости искомой величины к гармонической) приближенный метод не может обнаружить сложные виды автоколебаний и вы нужденных колебаний, о которых речь шла в §§ 5.5. 7.3. Но, с другой стороны, эти сложные виды автоколебаний и вынужденных колебаний могут иметь место лишь тогда, когда линейная часть системы не обладает резко выраженными резонансными свойствами и не является низкочастотным фильтром, т. е. тогда, когда необходимо учитывать высшие гармоники.

Обратимся теперь к сопоставлению результатов, касающихся устойчивости периодических режимов.

Следует отметить, что условия устойчивости периодических режимов частоты о с необходимой строгостью были получены на основе метода малого параметра *) лишь для систем с резко

*) См. Н, М. К р ы л о 8, Н. Н. 5 о г о л (О б о Б [1]. А. И. Л у р ь е [Ц.

выраженными резонансными свойствами (т. е. характеристика линейной части которых имеет вид рис. 11.12,с). Учитывая, что для релейных систем dS (Л,) 4fep

<0,

1 - 1

это условие устойчивости (с точностью до малого параметра) можно представить в виде

Это же условие безоговорочно фигурирует во всех работах, излагающих приближенный метод и изучающих системы, существенно отличные от тех, для которых оно справедливо.

1,27

0.2 D.f O.BDfi1

Ч В 8 ID ZD

Рис. 11.24. Сопоставление границ существования вынужденных колебаний в электрическом приводе, полученных точным (сплошная кривая) и приближенным (пунктир)

методами.

Условие устойчивости вынужденных колебаний в полосе захватывания, справедливое при тех же предположениях, что и условие устойчивости автоколебаний (11.98)*), применительно

*) Эти условия устойчивости в несколько иной форме были получены И. М. Смирновой [1], М. А. Айзерманом и И. М. Смирновой [Ц. Е. П. Прповым и И. П. Пальтовым (Ц.

к релейным системам, рассматриваемым здесь, можно привести к виду

ф|<90°, (11.99)

где ф - сдвиг фаз между внешним гармоническим воздействием и вынужденными колебаниями *).

Найдем теперь условие устойчивости автоколебаний из точных выражений для интересующих нас систем, линейная часть которы}? обладает частотной характеристикой вида рис. 11.12,6.

Для этой цели удержим в выражениях для /С и IF*(/со) только те слагаемые, которые зависят от со <: Зсоо.

Тогда, предполагая, что внешнее воздействие гармоническое, получим из (10.51) § 10.3, учитывая (11.78):

/<~=-Лсо8ф-2{/(соо), . (11.100)

а из (10.25) § 10.3:

= W + W (/ ((О - 2соо)) + W (/ (со + 2щ)). (11.101) В этом случае при со = (Оо

W* (/со) = W (/со) + Г (- /СОо) = 2U (сОо). (11.102)

Если линейная часть системы устойчива или нейтральна и W*(/co) не имеет при со coq пересечений отрезка (-оо, -/С ), то, как было показано в § 10.7, необходимые условия устойчивости автоколебаний приводятся к неравенству (10.69):

dim / (со)

Ш=СОг

>0. (11.103)

Но из (11.78) после дифференцирования получим Й1т/(ю) 4fep dim ir (ую)

do Я dco *

Так как

ImlF(/(o)=F(co),

то окончательно необходимое условие устойчивости автоколебаний найдем в виде

dV (со)

-1и=о

>0. (11.104)

Что же касается необходимого условия устойчивости вынужденных колебаний, то, как было показано также в § 10.4, оно при

*) При этом предполагается, что вневдиее воздействие приложено ко входу релейного элемента.

внешнем синусоидальном воздействии имеет вид

I Ф К 90°.

Но эти условия, полученные из результатов точного метода в предположении, что высшие гармонические составляющие выходной величины линейной части системы ничтожно малы по сравнению с составляющей основной частоты, совпадают с условиями (11.98), (11.99), к которым приводит приближенный метод.

Отсюда следует, что условия устойчивости, даваемые приближенным методом, в общем случае являются только необходимыми условиями.

Интересно отметить, что они необходимы не только для релейных систем, в которых линейная часть имеет резко выраженные резонансные свойства (и, следовательно, уравнения содержат малый параметр) *), но и для релейных систем, в которых линейная часть представляет собой низкочастотный фильтр.

В частном случае, а именно, когда кривая W*(/(o) не пересекает отрезка (-оо,-/(-) при со =/= соо, эти условия (с точностью до пренебрежения гармониками) являются необходимыми и достаточными.

Некоторые возможности различения этих случаев без построения кривой Р*(/(о), а непосредственно по частотной характеристике линейной части IF (/со), были рассмотрены в §§ 10.4 и 107. .

При учете высших гармоник, т. е. дополнительных слагаемых в Р*(/со), которыми мы выше пренебрегали, условия (11.102) и (11.103), вообще говоря, не являются ни необходимыми, ни достаточными.

*) Как это, например, следует из результатов работы М. А. Айзермана и И. М. Смирновой [1].