каждой точки и = too этого годографа построим согласно вы-пажению обобщенного годографа /(со, е) отрезки кривых, изменяя е до тех пор, пока эти отрезки кривых не пересекут ось ординат при е = Вт и ось абсцисс при е = ео (на рис. 11.8 значения Вт и Во обозначены через еш и 8,0 соответственно).

Для е = Вт

Re/(со, ej = - -5-

I Im/(co, ej==

= 0,

a для e=

Im / (со, Во) = -zlo = 0,

Re/(co, eo) I = 4-11-(so-2-)

= max-

(11.62) (11.63)

(11.64) (11.65)

\ J(u.O) \

Согласно (11.58) и (11.61) амплитудно-частотная характеристика релейной системы /?(со) определяется как

i?(co) = IIm/(co,eJ. (11.66)

Таким образом, отрезки оси ординат, отсекаемые кривыми /(со, е) при со = const и изменении е равны ординатам амплитудно-частотной характеристики при со = const. Очевидно, что /?(со) существует только при тех частотах со, для которых А Лкр. Отметим, что /?(со) не зависит от формы внешнего воздействия.

Фазо-частотную характеристику релейной системы 6д(со) можно определить как алгебраическую сумму сдвигов фаз z(<) и f(<) относительно ошибки х(0, т. е.

(со) = я), - ф = я (во - 1) - ф

или

e(co)==n(i-eo)-fr(-).

(11.67)

Таким образом, фазо-ча-стотная характеристика определяется значениями е = ео, при которых обобщенный годограф / (со, е) пересекает ось абсцисс; она зависит от амплитуды и формы внешнего периодического воздействия.

J(u.l)

Рис. П.8. К построению обобщенного годографа / (со, Е).

Если форма f{t) и z{t) близка к симметричной относительно их максимумов, то фазовые сдвиги можно определить приближенно по расстоянию между их максимумами (см. рис. 11.7).

В этом случае, полагая Фт = Ф + у. можно записать (и) е„ == зхе^ - Ф„ = зге„ - ф - =

= .(e.-i) + r(). (11.68)

Формулы (11.66) и (11.68) лежат в основе графоаналитического построения амплитудно-частотных и фазо-частотных характеристик, т. е. частотных характеристик релейной системы. Для простейших релейных систем частотные характеристики можно представить в аналитической форме.

Рассмотрим релейную следящую систему, передаточная функция непрерывной части которой имеет вид

По таблице 11.1 определяем /(со, е)-. В данном случае полюсы К{р) известны, поэтому удобно /(со, е) выразить через передаточную функцию в следующем виде:

Re / (и, в) =

(ЛТ..

1+е

1+е

(11.69)

1т/(со, е) = /гр/г,{(1-28) +(Г^+Г„)

1+е

1+е

(11.70)

Предположим, что релейная система имеет следующие параметры: Гм = 0,05, Гя = 0,03, kki = 75. При этих значениях /(ш)=/(со, 1) будет иметь вид, изображенный на рис. 11.9. Здесь же изображена /(ш, 0) == -/(ш).

Полагая со = const и изменяя е от О до 1, определяем кривые /(ш, е), соединяющие точки с равными а> на годографах /(со, 1) и / (со, 0). Значения е, при которых /(ш, е) пересекают оси координат, определяют Ът и ео, а значения ординат равны /?(ш).

Задаваясь, например, значением Л == 0,2 и пользуясь зависимостью Лкр от © (рис. 11.10), находим

ф

(11-71)

а затем по формуле (11.67) находим 0л(со). Зависимости Rita), ен(сй) изображены на рис. 11.10 для треугольной и прямоугольной форм внешнего воздействия. Частотные характеристики существуют при тех значениях со, для которых А Лкр.

-2,0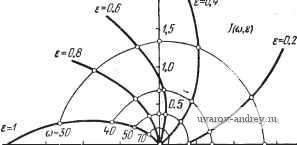

yReJ(u),&)

2.0 -1,5 <b OJD.S ] W \1,5 i*

Рис. 11.9. Обобшенный годограф / (со, е) релейной системы.

Предположим теперь, что Тп = 0. Тогда передаточная функция релейной системы имеет более простой вид:

(11.72)

((T-MP-f 1)р-

В этом случае /?(сй) и 0л(сй) могут быть выражены в аналитической форме. Действительно, из (11.69) и (11.70) при Гя = О находим

Re/((u, в)=-

(О

2е

2е

(11.73)

Приравнивая Re/(cu, е) нулю, находим е = е; :

соГм 2

1 + е

Подставляя это значение в Im/(co, е), получим

R{a) = \ Im/(co, е) [kkji

2(оГ

+ 1п-

1+е /

(П.75)

(11.76)

Для определения 0н((й) воспользуемся приближенным выражением (11.68); при е = е™, определяемом выражением

А

О -1,0 -10 -3.0

(11.75), будем иметь

= (йГ In -

1 + е

-- + 2

Z0 W

80 100 (J

+Г'(т^)- ( )

Вычисление точного значения 6д(сй) связано с решением трансцендентного уравнения *)

Im / (со. Во) = О

Рис. 11.10. Амплитудно-частотная и фазо-частотиая характеристики релейной системы.

относительно ео.

На рис. 11.11 изображены амплитудно-частотная и фазо-частотная характеристики рассматриваемой релейной системы для синусоидальной, треугольной и прямоугольной форм внешнего воздействия J{t), построенные по формулам (11.76) и (11.77) при Гм = 0,05, р^л = 75.

Отметим некоторые свойства релейных систем, позволяющие использовать их как фазосдвигающие устройства вынужденных колебаний любой формы. Подбирая соответствующим образом линейную часть релейной системы, можно получить вынужденные колебания любой формы.

) Выражения для /?(со) и 6д(со) в несколько иной форме были полу-К. Огата [1].

Если к релейной системе без зоны нечувствительности приложено периодическое воздействие и в ней существуют вынужденные колебания, то, как было показано в § 8.1, при увеличении амплитуды внешнего периодического воздействия А.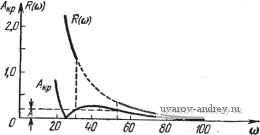

-3,0

Рис. пл. Амплигудяо-частотные и фазо-частотиые характеристики при г =0.

начиная с критического значения Л„р, сдвиг фаз вынужденных колебаний будет изменяться. Закон изменения этого сдвига фаз был приведен в табл. 8.1 (стр. 301).

Таким образом, в этих условиях релейная система представляет собой фазосдвигающее устройство или своеобразный нелинейный фазовый модулятор, в котором сдвиг фаз определяется величиной амплитуды внешнего периодического воздействия.

§ 11.8. Сопоставление результатов точного и приближенного методов

Для исследования периодических режимов в нелинейных системах и, в частности, в релейных системах широко применяется метод гармонической линеаризации или родственные ему методы медленно меняющихся амплитуд, метод малого параметра и др.*).

В основу всех этих методов положено предположение о том, что одна из величин, характеризующая состояние релейной системы в периодическом (установившемся) режиме, близка к синусоидальной функции. Физически это может иметь место, либо когда линейная часть системы характеризуется резко выраженными резонансными свойствами и нелинейность мала, либо когда линейная часть представляет собой фильтр низкой- частоты, т. е. не пропускает гармонических составляющих выше какой-либо определенной частоты**).

Первый сличай, которому соответствует частотная характеристика, изображенная на рис. 11.12, а, наиболее часто встречается в радиотехнических устройствах.

Второй случай, которому соответствует частотная характеристика, изображенная на рис. 11.12,6, является преобладающим в системах автоматического регулирования. Далее только этот случай и будет рассматриваться.

Для сравнения результатов, даваемых приближенным и точным методами, наиболее удобно воспользоваться частотной формой последнего, т. е. выражениями годографа /( ), процесса z(t) и функцииЦ7* (/и) через частотную характеристику линейной части системы.

Предположим, что частотная характеристика линейной части системы такова, что все гармоники, начиная с Змо, на выходе ее ничтожно малы и ими можно пренебречь. Примерный вид частотной характеристики показан на рис. 11.12,6. Тогда, удерживая в выражениях годографа /( ) (6.18) § 6.2 и z{t) (11.4) слагаемые, зависящие от частоты первой гармоники м = о, получим приближенные значения этих выражений в виде

/(со) .-1Г(/(о) (11.78)

м

*) См., например, работы Л. С. Гольдфарба [1], И. Я. Лехт-... а н а [1], Ж. Д юти ля [1] по исследованию автоколебаний, работы Р. Ко-хенбургера [1], [2], М. А. Айзермана [1], Л. С. .Г о л ь д ф а р б а [3] по исследованию вынужденных колебаний в релейных системах, а также работы Е.П.Попова [1,Е. П. Попова и И. П. Пальтова [1]. **) См. М. А. Айзерман [2].

и при отсутствии внешнего воздействия (z{t) = -x{t)):

z{t) = - ITo ((Oo) sin (co + e ((Oo)). (11.79)

Из этих выражений, являющихся первым приближением точных результатов, следует, что в этом случае годограф релейной

системы /((о) с точностью до

множителя совпадает с ча-

стотной характеристикой линейной части системы Ц7(/(о), а процесс действительно гармонический. .

jlmKul

ReKu)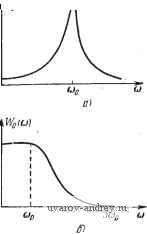

Рис. п.12. Вид Wo (со) при резко выражен- Рис. 11.13. Годограф J Щ. К определению ном резонансе (а) и при фильтрующем частоты автоколебаний Шо-

вой тве (б).

Воспользовавшись описанным выше способом, по годографу

/(со) = 1Г(/(о)

в точке пересечения ее с прямой -ио определяем частоту возможных автоколебаний (о = (Оо (рис. 11.13). Амплитуда этих колебаний найдется из уравнения 11.79) в виде

(11.80)

Но приведенное построение не отличается от построения, предложенного Л. С. Гольдфарбом [1], если его применять к релейным системам. Отметим, что для релейного элемента с гистерезисом эквивалентный комплексный коэффициент усиления, или коэффициент гармонической линеаризации, равен

5 (Л):

о

- Z3-/arcsin-7

Для определения вынужденных колебаний в полосе захватывания, вызываемых гармоническим воздействием, нужно, как

это было описано в § 8.1, из точки годографа /(со), соответствующей частоте внешнего гармонического воздействия м = мо, провести окружность радиуса, равного амплитуде внешнего воздействия А, и определить сдвиг фаз между вынужденными колебаниями и внешним воздействием. Выходная величина линейной части системы будет равна, так же как и ранее,

2 (f) = 1Го ((Оо) sin ( 0 -f е ( о)). , -

входная же величина нелинейного элемента будет равна x{t) ~ - Ai sin мо. Но согласно (7.4)

x(t) = Afo{t-cp)-z{t).

Поэтому

л, sin (i)at = A sin (©о^ - ф)--Wq( о) sin{а^ + G (соо)). (11.81)

В комплексной форме это выражение можно представить

д = Ле-<Р-5(Л,)Л,Го( о)е'е . (11.82)

где

= (11-83)

5(Л]) есть коэффициент гармонической линеаризации релейного элемента при хо = 0. Выражение (11.82) можно также переписать в виде

или

Соотношения (11.84) и (11.84) были положены в основу графических построений, примененных в работах Р. Кохенбургера [1], [2J, М. А. Айзермана [1], Л. С. Гольдфарба [3].

Найдем, пользуясь выражением (11.82), критические значения амплитуды и границы области существования вынужденных колебаний. Ввиду простоты S(Ai) надобность в графических построениях здесь отпадает. Подставляя S{Ai) из (11.83) в уравнение (11.82), найдем выражение искомой амплитуды вынужденных колебаний

Л, = Ле-ч- - 1Го ( о) ei

или, после отделения действительной и мнимой частей.

Л COS ф---- и (соо)

Л sin ф

4kr,

(11.85)

где и{а) и V(cu)-действительная и мнимая части U(/(o). Это соотношение содержит два неизвестных. Л: и ф. Так как -действительная величина, то мнимая часть в (11.85) должна быть равна нулю. Приравнивая ее нулю, находим величину ф = ф, из уравнения

4ki, F(fflc)

8Шф, = -

(11.86)

При этом искомая амплитуда найдется из уравнения

Л, = Л созф]

f/(coo).

(11.87)

Исключая из (11.86) и (11.87) фь окончательно получим

Ai = ~UM±VA-{JV4). (11.88)

Отсюда следует, что Л| > О и фаза ф1 существуют, если при t/(coo) < О

4k о

Л> Л, р = У(0о)1, (11.89)

а при и ((Оо) > О

Л > Лгкр = VU ( о) + (СОо) = 1Го (соо), (11.90)

т. е. если Л превышает критические значения.

Эти результаты следуют из точных выражений критических значений амплитуд (8.20), (8.22) § 8.2 (при хо = 0), если произвести замену годографа релейной системы /((о) согласно (11.78) частотной характеристикой линейной части И7(/(о). Подобным образом и в более общих случаях, например, при наличии зоны нечувствительности, ограничиваясь в выражениях для годографов релейной системы (6.61), (6.62) первыми слагаемыми при ш(0) = О, получаем (см. также (6.67), (6.68))

/.(со) /.(со)

4k а

-sin У

sin У

-5-Го(со)е V

Подставляя эти выражения в условия существования автоколебаний (6.57), (6.58), получим

4ko зх Г тс

уя + (1 - у)у -е(со) =-Хо,

- sin у-5- (м) sin

- sin у I Го (со) sin [(1 - у) f - е (со)] = Хщ.

Разрешая эти уравнения относительно

а (и) = Wo (со) cos е (и) и V (со) = Wo (со) sin е (со),

получим

[/(со)==-

л (1 -f Я) Ко 4kp sin vn;

К(со) = -

я(1 - Я) Ко 8/гр sinY

(11.91)

Из этих соотношений можно найти приближенное значение параметров м и у автоколебаний в релейной системе. Эти значения совпадают со значениями, полученными методом гармонической линеаризации*).

Из сказанного выше следует, что чем резче линейная часть релейной системы отфильтровывает основную гармонику, т. е. чем сильнее эта линейная часть уменьшает амплитуды высоких гармоник начиная с третьей, тем ближе к точным результаты определения условий существования амплитуды и частоты автоколебаний, а также сдвига фаз и амплитуды вынужденных колебаний по методу гармонического баланса и родственным ему методам (в смысле первого приближения к точным результатам)

Все эти результаты приближенных методов вытекают из результатов точного метода, если в выражениях годографов нелинейной системы удержать

Рис. 11.14. Релейная система с линейной частью первого порядка и релейным элементом с гистерезисом.

лишь первые слагаемые, соответствующие основной частоте, и отбросить члены соответствующих высоких гармоник. Неучет отброшенных гармоник может привести к количественной (а иногда и качественной) ошибке. Примером релейной автоматической системы, для которой метод гармонической линеаризации приводит к неверным результатам, является простейшая релейная автоматическая система, содержащая релейный элемент с гистерезисом и линейную часть первого порядка (рис. 11.14). Согласно методу гармонической линеаризации (рис. 11.15) заключаем, что поскольку нет пересечений обратного коэффициента гармонической линеа-

*) См. Н. А. Королев [5].