Зависимость

при (ЛоТы =(0о - 1,2, построенная по формуле (11.39) при учете первых трех членов, изображена на рис. 11.3 (кривая 2).

z(t)

Рис. П.З. Форма периодического режима в релейной следящей системе: кривая / построена по формуле (11.38), кривая 2 -по формуле (П.39).

Сопоставление этих кривых показывает, что для построения z{t) достаточно в (11.39) учесть несколько гармоник.

2. Электропривод. Определим закон изменения скорости электропривода при учете сухого трения на его валу. Согласно схеме (см. рис, 2.16) при синусоидальном движущем моменте угловая скорость привода равна

со f = со - Дсо„, (11.40)

где

co = f(0 =

sin((o/-ф'-arctgojlM). (11.41)

(Он есть скорость привода при отсутствии сухого трения, а Асои - изменение скорости, обязанное наличию сухого трения. Так как передаточная функция линейной части равна

то по формуле (11.25) находим выражение для А(йн(0 в виде

t -

Асо„ (О = ki где йо = йрйдв.

2е

1+е о^м.

0<<-

СОо

(11.42)

При/=Г = - величина Дсо„() принимает максимальное

значение, равное

1 е о^м ,

max Асо„ (t) = ko-~- = ko th

(11.43)

Найдем отношение max Асон(0 к амплитуде угловой скорости при отсутствии сухого трения, т. е. к тахсон(0:

max Асй„ (t)

Это отношение равно

max AOjj (/)

i = -l/W+lth.

(11.44) (11.45)

Зависимость М от юо = юом приведена на рис. 11.4. Величина М изменяется от 1 при й = О до 1,57 при йо = оо.

/V f,5

t,3 1,1

и

0,1 0,2 0,4 0fi0,81

4- 6 8 10 ZD

Рис. 11.4. Зависимость tA от о Для электропривода.

Эта зависимость позволяет определить влияние сухого трения на угловую скорость электропривода*).

*) Несколько иным путем эта задача была рассмотрена С. А. Лебедевым и Л, Н. Дашевским [1].

§ 11.6. Оценка формы периодического режима

Наиболее простым видом периодического режима является синусоидальный или гармонический режим. Рассмотрим отклонение периодического режима от синусоидальной формы. Для этой цели удобнее всего воспользоваться выражением z{t) в виде ряда Фурье, которое для простоты запишем в виде

2 (О = S 2m-i COS [(2m - 1) Шо/ - (2m - 1) у I + е ((2m -1) соо)].

(11.46)

где

Лгт-! -

Sin (2т- 1)у-

2т- 1

lFo[(2m-.l)(Oo].

(11.47)

Обозначим первую гармонику этого выражения через zi{t) так, что

Z, (t) = Al cos [(0(/ - + 8 (юо) .

Разность между 2{t) и zi{t), характеризующая мгновенное отклонение, равна

E(t) = z{t)-zi{t) =

= 2 Azm-yCOS

(2m - 1) (Оо< - (2m - 1) у I-4-е ((2m - 1) СОо)

Отличие периодического режима от синусоидальной формы определим при помощи коэффициента искажения ое:

л

£2 (/) dt

т2 =-

я о

(11.48)

Подставляя сюда значения E{t) и zi{t), получим

m=i2

(11.49)

Чем меньше амплитуды гармоник, тем меньше коэффициент искажений 0в.

Если в (11.49) заменить коэффициенты Azm-i их значениями из (11.47), то будем иметь

sin2(2m- 1) 2

WS[(2m -1)(0о]. (11.50)

Величина oe существенно зависит от вида частотной характеристики линейной части системы и параметров соо и у.

Чем быстрее (при прочих равных условиях) с ростом со уменьшается Wo (со), тем меньше ое, т. е. тем меньше отличие формы автоколебаний от синусоидальной. Полагая, что отно-

Го [(2т- )(Оо] Uo(cй)

равны единице, найдем а£=ар, который

соответствует коэффициенту искажения выходной величины релейного элемента

, sin42m-1)Y 2

* . я Xi~ (2m - 1)2

Обычно для реальных систем <С Ор- Замечая, что sin2 (2т - 1) у у = J - - cos (2m - 1) ул, запишем (11.51) следующим образом:

SsinYf

1 COS (2m- 1)уя

2j (2m- 1)2 2 (2m- 1)2

m=2. m=2

Воспользовавшись далее известными соотношениями *)

Zji (2m- 1)2 8

COS(2m- 1)уя л (л

(2т- 1)2

= f(f-ny)-

cos лу,

преобразуем к виду

я2у

Р с . 2

8smy-j

*) См. И. С. Градштейн и И. М. Рыжик [1].

Cfn =

(11.52)

Для релейных систем без зоны нечувствительности у = 1 и, следовательно,

<P-V Х- * =0.484.

(11.53)

Зависимость Ор от у приведена на рис. 11.5.

Из рассмотрения этой зависимости следует, что Стр достигает своего минимального значения, равного 29%, при у = 0,742.

Так как обычно Wo (со) с ростом и уменьшается, то действительное значение ств меньше Ор. В каждом конкретном случае

по формуле (11.50) мож- но вычислить коэффици-

ент искажений ов, оценивающий отклонение формы периодического режима от синусоидальной.

Так как период или частота периодического режима заданы, то неко-

0.2 0. ао 0.6

Рис. 11,5. Зависимость Ор от v.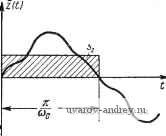

Рис. 11.6. Площадь периодического режима 5.

торой косвенной оценкой может служить площадь периодического режима (рис. 11.6). Найдем эту площадь:

z{t)dt.

(11.54)

Подставляя значение z(t) из. (11.46), после элементарных вычислений находим

I m-l

-i ~(2:-7)Г.?[(2-Осос]}. (11.55)

m=l

В частности, при у = I , .

*--Z< (2m-l)2 . (ll-5b)

Пользуясь ЭТИМИ выражениями, Sz легко определить непосредственно по частотной характеристике линейной части системы. Можно также определить Sz в замкнутой форме.

В ряде случаев может возникнуть необходимость оценки отклонения вынужденных колебаний z{t) or внешнего вынуждающего периодического воздействия f{t).

Пусть внешнее периодическое воздействие f{t) =Afo(at - Цl) можно представить в виде

f(t)= Afo {(at - ф) = 2 A/2m-l COS [{2m - 1) ©o< + (pm-l - 4>l m=l

где л и Ф таковы, что условия существования и устойчивости вынужденных колебаний частоты соо выполнены. При этом z{t) определяется формулой (11.3) или при у = 1 (11.4).

Величина отклонения x{t), определяемая соотношением (11.1), будет равна

X{t)-=f{t) - z{t) = y { Л/2т-1С05[(2т - l)cOji;-f ф2т+,-ф] -

(2m-l)(Oj/-(2m-l)Y + e[(2m-l)(Oo]}

- Am-i cos

ИЛИ, после элементарных преобразований,

(О = S Л^2т-1 cog [{2т - 1) ©Q< - Ф2, -,],

где

+ alfs/n-Hsm-i CQS (срг^ ) - Ф + (2т - I) у - 6 (2т - 1) Wo]}

и

= arctg

В качестве оценки процесса при периодическом воздействии можно применить среднеквадратичное отклонение Gx, определяемое соотношением

2л

aljit) lim

{t)dt.

где черта над xit) соответствует усреднению x{t) по времени, т. е. операции, указываемой правой частью этого соотношения. Учитывая периодичность x(t),

нетрудно преобразовать к виду

X СОо

2(0 dt.

Подставляя сюда значение x{t), получим

оо сзо

m=! m=l

+ 2/L-H2m-i COS [ф2т-1 Ф + (2m - 1) У - 6 ((2m - 1) coo)]}.

Эта формула позволяет вычислить среднеквадратичное отклонение релейной системы при периодическом внешнем воздействии по частотной характеристике линейной части системы.

При практических вычислениях часто в этой формуле можно ограничиться несколькими первыми членами.

Отметим, что выражение а^ = х^(0 можно получить в замкнутой форме через полюсы передаточной функции линейной части.

Аналогичным образом можно оценить форму процесса в релейных автоматических системах с несимметричной характеристикой релейного элемента. Само выражение процесса в этом случае определяется по переходной характеристике формулой

(3.16) § 3.3, а по частотной характеристике -формулой (5.71) § 5.6.

Для подобного рода релейных автоматических систем важной характеристикой процесса является среднее значение выходной величины линейной части системы. Зависимость этого среднего значения от постоянного воздействия характеризует статические свойства системы регулирования. Это среднее значение, т. е.

2п

2ер = г() = - J zit)dt,

определяется постоянной составляющей выражения для процесса, представленного в виде ряда Фурье (5.71) § 5.6, т. е.

2ер = [Уо+р(2у,-1)]1о(0).

При этом предполагается, что постоянное воздействие fn приложено к входу релейного элемента. Если постоянное воздействие приложено к линейной части системы так, что передаточная функция ее участка между точкой приложения внешнего воздействия и выходной величиной равна Wf(p), то в этом случае, производя, как было описано в § 2.1, пересчет его к входу релейного элемента, найдем выражение для гср в виде

гер = [Уо-/гр(2у,-1)]Го(0) + №(0). (11.57)

Таким образом, в этом случае среднее значение существенно зависит от величины внешнего воздействия fn и относительной длительности замыкания yi. Последняя величина определяется из исследования автоколебаний.

§ 11.7. Частотные характеристики релейных систем

В тех случаях, когда релейная автоматическая система работает в условиях периодического внешнего воздействия, важными величинами, характеризующими качество ее работы, являются максимальные значения выходной величины и сдвиг фаз между выходной величиной и внешним воздействием.

Зависимость этих величин от частоты внешнего периодического воздействия при постоянной амплитуде последнего определяет собой частотные свойства релейной системы.

Назовем частотной характеристикой релейной автоматической системы зависимость максимума выходной величины непрерывной части (или ее участка) от частоты внешнего периодического воздействия произвольной формы и зависимость сдвига фаз между выходной величиной z{t) и внешним воздействием f{t) от частоты последнего (рис. 11.7). Максимальное

отклонение внешнего периодического воздействия при этом предполагается постоянным. Таким образом, частотная характеристика релейной автоматической системы включает в себя амплитудно-частотную характеристику

R(a)= max \z(t)\ (11.58)

о<<<

И фазо-частотную характеристику

бд (и) = arg f (О - arg г (О = - ф + ф.

(11.59)

Для определения амплитудно-частотных и фазо-частотных характеристик введем понятия обоби^енного годографа релейной автоматической системы с идеальным релейным элементом

/(со, = -

где О е 1. При е = 1 обобщенный годограф релейной автоматической системы /(и, е) совпадает с обычным годографом /(со, 1) = /(со).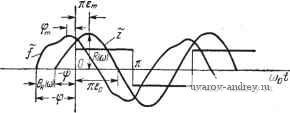

Рис. пл. К определению частотной характеристики релейной автоматической системы.

Будем изменять в от О до 1; тогда 1т/(со, е) определит форму периодической величины -zit) я , а Re/(co, е) с точностью

до масштабного множителя - определит форму ее производной

- 2~() ji . При этом z{t) описывается выражениями, приве-

денными в §§ 11.2, 11.3. Для удобства различные формы представления

и

Im/(co, е) = -zE-j приведены в таблице 11.1.

Обобщенный годограф !(&, г)

Re / (и, Е)

Im / (и, Е)

cos(2/n- 1)еяХ

X f/{(2m-l)(o)-sin (2/п-1)елХ XV ({2т-Da)]

sin (2m - 1) ejt 2m- 1

Xf/((2m- l)(o) + cos (2m - 1) eit

2m- 1

F((2m- Пю)

(4)

(.-I +e)

+ V ( )дл +e)-2-j

Cvo-

л

л

1 V

00 + Zj vo

p -

4(l-2e) +

л

Примечание. В форму.11ах графы 3 полюсы pv (v = l, 2.....и)

различны и отличны от нуля. В формулах графы 3 один из полюсов

/ Р(0) равен нулю и Сдо = qq)-

Нетрудно показать, что /(и, е) удовлетворяет соотношениям Re/(co,e) = iiH. /(со. 0)=-/(со, 1).

Для определения амплитудно-частотной и фазо-частотной характеристик релейной автоматической системы воспользуемся годографом релейной системы /(со) =/(со, I) (рис. 11.8). Из