(10.122), получим

- U + 6 *°

СОо

(10.124)

Если значения т = - и соо==сооГ соответствуют области /

(рис. 10.20), то правая часть неравенства (10.124) будет отрицательна и условие устойчивости вынужденных колебаний частоты соо будет выполнено, если

Л>Л, р, (10.125)

т. е. если выполнено условие существования этих вынужденных колебаний. Если же значения т и йо соответствуют области , то правая часть неравенства (10.124) будет положительна, и для

0.75

0.15

Обпасть устоачаВых Вынужденных колебаний

0.5 1.0 1.5 2.0 15 .iO 5.5 40 .5 (Ьд Рис. 10.21. Граница устойчивости вынужденных колебаний.

устойчивости вынужденных колебаний данной частоты необходимо, чтобы амплитуда внешнего гармонического воздействия А превышала на определенную величину критическое значение Л, кр. В этом случае из условия устойчивости (10.124) получаем

Л <

Л?кр +

п \2 N 2ПТ

СОо

(10.126)

На рис. 10.21 изображена граница устойчивости вынужденных колебаний, построенная по формулам (10.125) и (10.126) при т == 0,5 и к~ 0. Граница устойчивости до точки а совпадает с границей существования вынужденных колебаний. После точки с она проходит выше границы существования вынужденных

колебаний (пунктирная линия). Область устойчивости лежит выше границы устойчивости (сплошная линия).

Если вынужденные колебания частоты соо устойчивы, то автоколебания в системе (определяющиеся тем значением со, при котором Л1кр обращается в нуль) будут подавлены.

Для субгармонических колебаний выражение для Ч^*(р) совпадает по форме с уравнением (10.114), но теперь следует принять во внимание, что соц - -~, где v = 3, 5, 7, ..., п.

5Г( ф) + /()]. (10.127)

Причем, здесь согласно (8.44)

Re 9 (vjt - ф) = Л vf {ул

Ф).

(10.128)

Границы устойчивости субгармонического режима определяются по тем же соотношениям, что и границы устойчивости вынужденных колебаний основной частоты. При этом в (10.119) -

г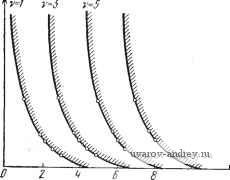

10 12 (Jg

Рис. 10.22. Границы различных условий устойчивости субгармонических колебаний.

(10.120) производятся указанные выше подстановки, в частности, щ = ~-. Таким образом, условия устойчивости субгармонических колебаний запишутся в виде

Avfj(vrt -ф)<0 (10.129)

Avf (то-ф)<

4е

(10.130)

рде юв = сов^м. Границы областей различных условий устойчивости для субгармоник порядка v теперь будут иметь вид

(10.131)

Они отличаются от (10.121) лишь измененным в v раз масштабом оси абсцисс (рис. 10.22). Для каждого v с незаштрихован-ной стороны справедливо условие (10.129), а с заштрихованной-условие (10.130).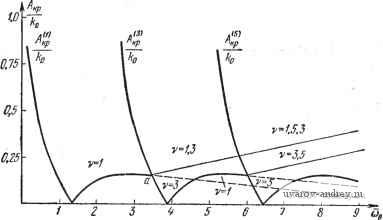

Рис. 10.23. Граница устойчивости субгармонических колебаний.

В частном случае, при гармоническом воздействии f о ( в^ - ф) = sin (сов^ - ф)

имеем из (10.122)

Av cos {vn - ф) = cos ф > О, т. е., как и ранее, ф| < 90°, а из (10.122) получаем

Лс05ф>-

(10.132)

Таким образом, условия устойчивости принимают вид

л>л',1р. (10.133)

Если параметры f и лежат с незаштрихованной стороны

границы (рис. 10.22) и

А>

.1 кр

k 4е

nv 2.,!

СОв

(10.134)

Границы устойчивости субгармонических колебаний v = 3 и v = 5, построенные по формулам (10.133) и (10.134), изображены на рис. 10.23. Здесь же приведена и граница устойчивости для основного вынужденного колебания (v = 1). Область устойчивых субгармонических колебаний находится выше соответствующих границ устойчивости.

В начальной части граница устойчивости совпадает с границей существования субгармонических колебаний. Затем граница устойчивости (сплошная линия) проходит выше границы существования субгармонических колебаний (пунктирная линия).

2. Система автоматической стабилизации курса самолета.

В § 6.7 мы исследовали существование автоколебаний в системе автоматической стабилизации курса самолета и установили, что автоколебания при отсутствии гистерезиса (х = 0) соответствуют областям 5 и плоскости параметров ai, аг (см. рис. 6.36).

Как видно из рис. 6.37 для области 4 (рис. 6.36) мнимая часть годографа /(со), проходя со == соо, убывает (рис. 6.37,г),

1 <0, а для области 5 (рис. 6.36) мнимая

часть годографа, проходя значения со = соо, возрастает (см.

рис. 6.37,в), т. е.

d Im / (со)

>0.

Ci3=COo

Следовательно, область 4 (см. рис. 6.36) соответствует неустойчивым автоколебаниям.

Что же касается области 5 (см. рис. 6.36), то в ней необходимое условие устойчивости автоколебаний выполняется. Для определения достаточных условий устойчивости можно было бы составить уравнение, решающее вопрос об устойчивости, и применить к нему алгебраический критерий устойчивости. Но, несмотря на эту возможность, такой путь для исследования в общей форме был бы крайне громоздок. Поэтому мы применим здесь качественное рассмотрение этой задачи, основанное на частотном критерии устойчивости.

В области 5 частотная характеристика линейной части, как было упомянуто в § 6.7, имеет вид (см. рис. 6.39,в), воспроизведенный на рис. 10.23, причем частота автоколебаний соо близка к СОгр.

Для Юо условие (10.42) выполняется, следовательно, в этом

d Im / (со) 1

> О является и до-

j W(jU}

случае необходимое условие

статочным. Поэтому для области 3 (см. рис. 6.36) автоколебания частоты юо будут устойчивыми.

Аналогичным образом нетрудно установить, что при наличии гистерезиса области У (рис. 6.36) будут соответствовать устойчивые автоколебания частоты юо (рис. 6.40,в). Области 4 (рис. 6.36) при небольших ио будут соответствовать неустойчивые автоколебания Юо и устойчивые автоколебания юЗ(рис. 6.40, г).

Таким образом, без всяких вычислений качественным путем мы исследовали устойчивость автоколебаний рассматриваемой системы.

8. Система автоматического регулирования температуры. Если релейный элемент обладает гистерезисом, то, как было показано в § 6.7, в системе автоматического регулирования температуры будут иметь место автоколебания. Зависимость относительной частоты

(для системы без жесткой внутрен-

Рис. 10.24. Вид частотной характеристики линейиой части дли значений параметров (oi, аг), принадлежащих области 3 (рис. 6.36).

этих автоколебаний от

ней связи) приведена на рис. 6.43. При

: 0,015 относитель-

ная частота автоколебаний юо, определяемая по этому графику, равна 3,7.

Исследуем устойчивость автоколебаний этой частоты. Как видно из рис. 6.42, необходимое условие устойчивости автоколебаний выполняется.

По действительной б'(ю) и мнимой V{a) частям частотной характеристики Wijai), приведенным на рис. 6.41, построим t/*(cu) и V*((b), как это показано на рис. 10.25, о и б. Здесь изображен лишь участок для О < ю < 2юо. Кривая

построенная по этим данным, приведена на рис. 10.26. Так как линейная часть системы устойчива, то из рис. 10.26 заключаем, что и автоколебания частоты юо = 3,7 устойчивы, ибо W* (/ю) при ю = Юо находится в третьем квадранте и, кроме точки ю==Юо, отсутствует пересечение отрезка (-оо,-/С~).

Таким образом, в этом случае устойчивость автоколебаний может быть определена непосредственно по годографу релейной системы (см. рис. 6.42).

При наличии зоны нечувствительности частота автоколебаний й и параметр у определяются абсциссой и ординатой точки пересечения кривых у = ri(w) и у = Г^(й).

8 Ю 12 й

Юд У

Л'*

Ъ 6 8 10 а

> Рис. 10.25. Построение U* (со) по U (со) (а) л V* (со) по V (со) (б).

На рис. 10.27 воспроизведены кривые Ti{(b) и ГгСй), соответствующие Но/ко = 0,03 (см. рис. 6.47,6).

Проводя касательные в точке их пересечения, заключаем, что необходимое условие устойчивости выполняется, так как < 90°. Можно показать, что в этом случае это необходимое условие является и достаточным.

Рассмотрим вкратце устойчивость вынужденных колебаний в системе регулирования температуры без зоны нечувствительности, возможность существования которых была изучена в § 8.6.

Зависимость AiKp в функции частоты (см. рис. 8.24) определяет область существования вынужденных колебаний, а те значения со, при которых

W*(joj)

0 = Ыд

= О, соответствуют возможным частотам автоколебаний.

Вынужденные колебания, для которых !ф| >90°, неустойчивы. Обратимся к исследованию устойчивости вынужденных колебаний, для которых ф| < 90° и которым на рис. 8.26 и 8.27 соответствуют как области /7, так и области /.

Для этой цели заметим, что частотная характеристика линейной части системы

-0,1

О

-0.1-

-0,2-

Рис. 10.26. Кривая W* (/а).

(рис. 6.42) имеет при любом ю отрицательную действительную часть, т. е. расположена во и / квадрантах, и для частот,

удовлетворяющих условию (10.43), кривая 1*(/ю) будет пересекать действительную ось только при й =

Отсюда следует, что вынужденные колебания на этих частотах при IфI < 90° будут устойчивы.

Аналогичным образом можно было бы, не строя W*{\ih) (см. рис. 10.26). установить устойчивость автоколебаний.

4. Электрический привод. В заключение рассмотрим устойчивость вынужденных колебаний скорости электропривода при синусоидальном действующем моменте и наличии на валу сухого трения. Передаточная функция линейной части равна

8 ы

Рис. 10.27. К определению устойчивости автоколебаний при наличии зоны нечувствительности.

W{p)-

а частотная характеристика

(10.135)

(10.136)

Ей соответствует полуокружность (рис. 10.28), причем

Н = -7#- (10.137)

Г„сй + 1

Так как

т{0)=Пт pW{p) = -¥= О, (10.138)

р- -оо м

то, как это указано на стр. 337 и в Приложении 2,

= 5] 1Г(/(а) + 2тсйо)). (10.139)

Поскольку Im 1Г(/(о) = 1/(сй) < о (см. (10.137)), то и ImlF*(/co)<0 при со < СОо. Следовательно, IF* (/и) будет подхо-j-yj дить к отрицательной действительной

оси при и -> СОо в третьем квадранте. Отсюда следует, что необходимое

условие устойчивости вынужденных ко- лебаний является и достаточным, т. е. --J-J условием устойчивости вынужденных ко-

V/l лебаний является неравенство (10.55) -- Л/(зт-ф)<0, (10.140)

которое для синусоидального воздей-

Рис. 10.28. к определению СТВИЯ Л 51П (сОо^ - ф) СВОДИТСЯ К ВИДу устойчивости вынужденных

колебаний^ легстропривода COS ф > О ИЛИ ф < 90°. (10.141)

Это условие устойчивости, как видно из изображенного на рис. 8.28 годографа релейной системы /(со), совпадает с условием существования вынужденных колебаний. Итак, если в электрическом приводе существуют вынужденные колебания, то они устойчивы.

Глава XI

ОПРЕДЕЛЕНИЕ ФОРМЫ ПЕРИОДИЧЕСКИХ РЕЖИМОВ

§ ПЛ. Форма периодических режимов

В предыдущих главах были установлены условия существования периодических режимов (автоколебаний и вынужденных колебаний основной частоты и субгармоник) и. исследована их устойчивость. Были изложены методы определения частоты автоколебаний соо, сдвига фаз ф между вынужденными колебаниями и внешним воздействием при заданной амплитуде последнего.

Дальнейший этап исследования периодических режимов состоит в определении их максимальных величин ( амплитуд ) и формы. Знание максимальной величины периодического режима и зависимости ее от параметров системы и внешнего воздействия крайне важно для оценки влияния этого режима на процесс регулирования.

Что же касается формы периодического режима, то построение его позволит проверить в каждом конкретном случае то допущение об отсутствии дополнительных переключений, которое было принято ранее при исследовании периодических режимов.

В силу специфического вида характеристики релейного элемента фор)ма периодических режимов на выходе линейной части системы, т. е. z(t), предопределена. Она представляет собой реакцию системы на периодическую последовательность прямоугольных импульсов у (<)-выходную величину релейного эле мента, частота и длительность которых известны из исследования условий существования периодических режимов.

В релейных автоматических системах без зоны нечувствительности для этой последовательности импульсов всегда у = 1. Отсюда следует, что форма и величина внеп1него воздействия, приложенного ко входу релейного элемента, не влияют на форму выходной величины линейной части системы, а лишь изменяют сдвиг фаз между внешним воздействием и вынужденными колебаниями, если последние существуют.

В релейных системах с зоной нечувствительности от формы и величины внешнего воздействия зависит длительность (т. е. величина у) импульсов, воздействующих на линейную часть системы, а следовательно, зависит и форма z{t).

По своим закономерностям автоколебания и вынужденные колебания z{t) в релейной системе весьма близки друг к другу, так как и в том и в другом случаях, как уже было сказано выше, они представляют собой реакцию линейной части системы на периодическую последовательность прямоугольных импульсов y{t). Благодаря этому периодический режим z{t) при найденных значениях шо, у может быть определен исходя из рассмотрения поведения разомкнутой релейной системы при периодическом воздействии, как это было описано в § 5.2.

Зная z(t), легко определить входную величину релейного элемента по известному соотношению

x{t) = Ah{cot~(p)~z{t). (11.1)

Если внешнее воздействие fi(t) приложено не ко входу релейного элемента, как это предполагалось всюду ранее (рис. 11.1,0), а, например, ко входу линейной части системы

-Н2)-*

Ч2ь

y(t)

Рис. U.I. Различные точки приложения внешнего периодического воздействия

(рис. 11.1,6), то выходная величина линейной части системы, очевидно, будет равна

2(0 + Г (0. (11-2)

где f(0 есть установившаяся реакция линейной части системы на воздействие fi(0, которая может быть определена способом, описанным ниже. Если нас интересует форма автоколебательного процесса, то в (11.1) и (11.2) следует положить ](t) s О, fi(0 0.

Таким образом, задача определения формы периодического режима сводится к определению z{t). Но эта задача уже была решена при рассмотрении поведения разомкнутой релейной системы при периодическом воздействии (см. § 5.2). Для построения периодического режима нужно воспользоваться этими ре-