Кроме того, как и ранее (см. формулу (10.40)),

*(М-щ;Нщ). (10.81)

Коэффициенты /Cv и АТ равны

= - 1 - Ф) + /v ( )]. /сг = - Re (я - Ф) + /, (со)].

(10.82)

р

Подставляя все эти значения в (10.77), найдем после соответствующих преобразований необходимое условие устойчивости периодических решений в виде

Re (я - ф) Re {[Г (уя -q>) + Jy Ы] + Uy Ы - / (с^о)]} +

-f Re (уя - ф) Re {[ (я - ф) + /, ( )] + [/, Ы ~ / (сОо)]} > 0.

(10.83)

При Y = 1 имеем

(со) = 7, (со) = 7 (ш) (10.84)

и, следовательно, из (10.83) получим

Re (я - ф) 2 Re (я - ф) + / (сОо)] > 0. (10.85)

Так как всегда Re[(я - ф)/(соо)] < О, то мы приходим к ранее полученному условию устойчивости вынужденных колебаний в релейной системе без зоны нечувствительности

Re(я-ф)<0. . (10.86)

Величины, входящие в (10.83), можно определить непосредственно по графикам семейства /i(co), / у(со) (рис. 10.17).

Заметим, что Re[{n - ф) --/i(coo)], Re[S{yn - Ц))-{-1у{(йо)] всегда отрицательны. Если Re [/i (соо) -/(соо)] и 1е[/(со)-/(соо)] также отрицательны или по абсолютной величине меньше, чем соответствующие им слагаемые, условие (10.83) будет заведомо выполнено, при

Re (я - ф)< О, Re (уя - ф)< О

I (10.87)

Для исследования устойчивости автоколебаний нужно положить Л = О, а значит, (уя -ф) = (я - ф) = 0. Тогда неравенство (10.77) обращается в равенство

-K7Kr = W Цщ), (10.88)

что свидетельствует о прохождении кривой W*(;cu) через точку (-/С^ЧГ,/о), т. е. о наличии у уравнения Ч^*(р) = 0 чисто мнимого корня р = /соо-

ReJ((j]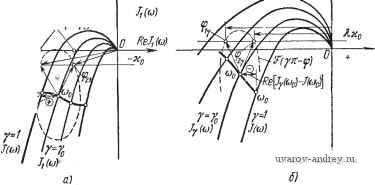

Рис. 10.17 Определение необходимого условия устойчивости вынужденных колебаний по годографам /, (ю) (а) и !у (ю) (6).

Для выяснения устойчивости авгоколебаний аналогично предыдущему рассмотрим поведение W*(;co) при со, близких к соо, т. е.

dW* (/со)

d(i>

dW (/со) dco

Ю=Н>о

Дсо, (10.89)

где W*(/co) определяется выражением (10.72), а Ку \ Ki - выражениями (10.82), при (уп - ф) = (л -ф) = 0. Вычисляя

dW (/со)

аналогично предыдущему получим

dW* (/со)

>=ю„

, после преобразований

tu=C0a

-Im/,(coo)Im/,(coo)}. (10.90)

Знак этого выражения определяет поведение W*(/co) вблизи со = СОо- Аналогично предыдущему заключаем, что если величина

W (j(o)

(10.90) положительна, то переход W*(/cu) при со = о через отрезок (-оо, -К'К^) отсутствует (кривая / на рис. 10.18). Если величина (10.90) отрицательна, то W*(/co) при со = ©о совершает половину перехода (кривая 2 на рис. 10.18).

Знак выражения (10.90) можно установить непосредственно по кривым у = El (со) и у = = Гу(©), определяющим параметры колебаний у и ©о. Эти кривые, как было показано в § 6.3, эквивалентны уравнениям

Im /, (©) = -Ио, 1т/(©о) = Яхо. (10.91)

Рис. 10.18. Поведение (/со) при

со >(В„.

Как известно, тангенсы углов наклона кривых, определяемые неявными уравнениями в точке их пересечения, равны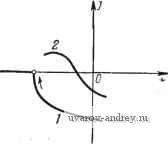

giti =--/

Im /, (соо)

Im /, (Шо)

Im ly (юо)

(10.92)

Обозначим через угол между касательными к кривым Y\ и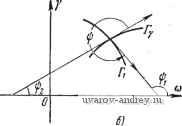

Рис. 10.19. Определение необходимого условия устойчивости автоколебаний по кривым Г| и : я)--необходимое условие выполняется, б) необходимое условие не в ыполняется.

Гг В точке их пересечения (рис. 10.19). Очевидно, что

= -Vl52. (10.93)

Следовательно,

sinif) = sin(il), - ifa) = sin ipi cosifa- cos if), sinifa. (10.94) Ha основании известных тригонометрических тождеств - .

simi),

cos %

/1 -i-fgj

(i=l, 2) (10.95)

выражение sin if можно представить в виде:

tg ф! - tg я]?;

sin if)

l(H-tg=ii)i)(l+tg2ii )

(10.96)

Подставляя теперь значения tgifi из (10.92), получим окончательно:

sin If =

-Tf f -v (®o) Im /i Ы - ~ Im /, (coo) Im / (coq) , у AB L acoo d\ dtoo dy

(10.97)

где

= Im /, (coo)] + Itn /i ( o)

Im/(a)o)]4-[Im/(oo)

(10.98)

Отсюда следует, что знак выражения (10.90) совпадает со знаком sin if J где if - угол между касательными к кривым Fi и Ту в точке их пересечения. Если sinif > О, т. е. О < if < п, то переход W*{j(i)) при со = о через отрезок (-оо, КуКГ) отсутствует (см. рис. 10.18, кривая /). Если sin if < О, т. е. я < if < 2я, то W*{ja) при со = СОо совершает половину перехода (рис. 10.18, кривая 2). Если в точке пересечения кривых Fi и 1\ провести векторы, касательные к ним, и имеющие положительное направление*), то необходимое условие устойчивости автоматически будет выполнено, если вектор Ту, двигаясь против часовой стрелки, при совмещении с вектором Fi описывает угол меньше 180° (рис. 10.19,а), и не будет выполнено, если описываемый при этом угол больше 180° (рис. 10.19,6).

Таким образом, необходимое условие устойчивости определяется непосредственно по графикам кривых y = ri(co), у = = Fy(co), определяющих параметры автоколебаний.

Характеристическое уравнение релейной автоматической системы с зоной нечувствительности может быть получено из выражения

(р) = 1 + (/, + /,)г'(р) +

+ т KtKy [W (р) - vr (p. у) г* (р, - у)], (10.99)

*) То есть такое, при котором малое увеличение Хо смещает кривые Ti }i Гу влевр от этого направления.

где W*{p, у), W*{p, -у) определяется формулами

(9.106), (9.96), (9.99). Положив в (10.99) е <<> = и и приравнивая числитель нулю, получим характеристическое уравнение. К этому характеристическому уравнению применимы алгебраические критерии устойчивости.

§ 10.5. Релейные системы с несимметрией

Для релейных автоматических систем с несимметричной характеристикой релейного элемента без зоны нечувствительности, но с гистерезисом, как видно из (9.88), W*{p) выражается также в виде комбинации W*{p) и W{p, ±у). При р =/ю из (9.88) получаем

1г*(/сй)=аду1г*(/сй). (10.100)

Здесь

W(/со) = {Ку + /сг)(/со) + W(/со) - (/со, Y,)(/со, -Y,)].

(10.101)

Во kfi + Йр2 СОо kpi -Ь k

(10.102)

W{h)-~W{ji>), 1Г'(/со, ±у,) = :1Г'асо, ±Y,). (10.103)

Вопрос об устойчивости периодического режима решается при помощи частотного критерия устойчивости (§ 10.1) путем подсчета числа и знаков перехода кривой IF* (/со) через отрезок {-оо, - i/Cr). При этом кривые W*(/co, ±Yi) строятся по

± со

кривым W Ц(л) е , которые определяются выражением, аналогичным (10.76). Необходимое условие устойчивости и его геометрическую интерпретацию можно получить путем рассуждений, подобных проведенным выше. Нетрудно получить характеристическое уравнение релейной автоматической системы с несимметрией. Для этого в выражении

+ KiKy[WAp)-WAp,ydW{p,-yi)], (10.104)

нужно положить е > =и и приравнять числитель нулю. К полученному характеристическому уравнению можно применить алгебраический критерий устойчивости.

§ 10.6. о влиянии случайных воздействий на периодические режимы

Наличие случайных воздействий - флуктуации - в релейном элементе или непрерывной части изменяет периодический режим. Оценим изменение периодического режима, вызываемого воздействием случайных помех. Будем рассматривать случайные помехи как дополнительное внешнее воздействие t,:

f{t)=f{t)+m. (10.105)

При этом периодический режим нарушается, и ошибка теперь будет равна

где 1(f) - отклонение от периодического режима. Если случайные помехи достаточно малы, то (/) будет определяться уравнениями в вариациях (9.35), (9.56), (9.60), (9.67), (9.70), (9.79), которые были установлены в главе IX.

Исследование воздействий случайных помех на периодический режим сводится к статистическому анализу импульсной системы. Для этой цели можно воспользоваться стандартной методикой.

Пусть случайные помехи стационарны и их спектральная плотность и корреляционная функция равны соответственно

5(со), Rln - ]. Спектральная плотность и корреляционная

функция отклонения от периодического режима найдутся по известным соотношениям

5 (сй) = Г(/сй)р5(сй),

m=i-oo Г=-оо

(10.106)

где ( j - импульсная характеристика импульсной системы, равная обратному дискретному преобразованию передаточной функции К*{р).

Зная выражения 5(со) и определяем среднее

значение квадрата отклонения от периодического режима по формулам

о

или

П=-с Г=-с

(10.108)

Полученные формулы и решают поставленную задачу*). Аналогичным образом можно получить выражения для среднего значения квадрата отклонения и в более общих случаях, но мы эти более сложные формулы приводить здесь не будем.

§ 10.7. Примеры

После выяснения общих закономерностей, касающихся устойчивости периодических режимов в релейных автоматических системах, обратимся к рассмотрению конкретных релейных систем.

1. Следящая система. В § 8.6 были найдены области су шествования вынужденных колебаний, отличающихся сдвигом фаз. Согласно необходимому условию устойчивости (10.55), заключаем, что вынужденные колебания, которым соответствует сдвиг фаз ф| > 90°, заведомо неустойчивы.

Исследуем устойчивость вынужденных колебаний, для которых ф| < 90°. Для этой цели применим ввиду простоты системы алгебраический критерий устойчивости. Передаточная функция линейной части следящей системы равна

Предположим, что т < - (это всегда выполняется при не

СО©

очень высокой частоте вынужденных колебаний). Тогда в соответствии с формулой (9.122) при / = 0 получим выражение для

функции W* (p) = -W(p) в виде

(10.110)

Далее, согласно формуле (10.52)

= - ф) + / (СОо)],

Re S? (я - ф) = Л/о (я - ф),

*) См. также А. А. Первозванский [1].

(10.111) (10.112)

Н согласно (6.101) (см. § 6.7) при /=1

1-2-

1+е

(10.113)

Следовательно, уравнение для Ч^*(/?) будет иметь вид Ч^*(р)=1+/СГ(р) =

-1 + /С-

лил

СОо

0 -е м-о

= 0, (10.П4)

где

Полагая здесь е = м и приводя выражение (10.114) к общему знаменателю, запишем числитель в виде

goU + glU + §2 = 0,

где

+ l).

(10.115)-

(10.116)

Подставляя значения go, gi, g2 в неравенства (10.18), получаем условия устойчивости

go + + g2 = (l - е~) > О,

go-gi+g2 = 2К- (l + е ) -

(10.117)

Из второго и третьего неравенств находим условия устойчивости вынужденных колебаний,

2соо

1+. л

(10.118)

лкл

(10.1180

Подставляя в левые части неравенств (10.118) и (10.118) выражение К' из (10.111) (предварительно заменив в нем Ке(я -ф) и Re/((uo) их значениями из (10.112) и (10.113) соответственно), после несложных преобразований получим условие устойчивости вынужденных колебаний частоты соо в виде

Л^(я-ф)<-

Л/о(я -ф)<0

я Y я

,1 +6) -4е®

(10.119) (10.120)

где ко = kpkj, й = сооГ , =

Первое из условий устойчивости (10.119) представляет собой необходимое условие устойчивости, полученное ранее. Выполнение этого условия проверяется при определении условий существования вынужденных колебаний частоты соо. Что же касается второго условия устойчивости (10.120), то оно в силу (10.119) заведомо выполняется, если правая часть неравенства (10.120) положительна. Если же правая часть неравенства отрицательна, то условие (10.120) накладывает дополнительное ограничение на Л и ф.

Правая часть неравенства обращается в нуль при

я \2

T = lnch.

(10.121)

Эта зависимость т от йо изображена на рис. 10.20. Здесь же показан характер кривой Р*(/й). Если значения т и йо принадлежат области /, находящейся с незаштрихованной стороны кривой, то устойчивость вынужденных колебаний полностью определяется условием (10.119), т. е. непосредственно по

15 W 0.5

О

W ijO) +

4 йо=<->в

Рис. 10.20. Граница различных условий устойчивости вынужденных колебаний.

годографу релейной системы /(й). Если значения f и й принадлежат области , находящейся с заштрихованной стороны кривой, то необходимо дополнительно наложить ограничения на А и ф. Пусть внешнее воздействие синусоидально, т. е.

f о (соо^ - Ф) = sin (соо^ - ф).

Тогда условия (10.119) и (10.120) преобразуются к виду

Л cos ф > О, т. е. 1 ф К 90°

feo 46 -

1+е

, 0 )

А cos ф > -

СОо 2

Но, как было показано в § 8.1 (формула (8.23))

1 кр

(10.122)

sin ф

Следовательно,

Лсо8ф=Л /1 -81п2ф = 1/Л2А2

1 кр

(10.123)

Производя замену Лсозф его значением (10.123) в неравенстве