Пользуясь графическим способом суммирования векторов

g- * 1 wk ) или любым способом синтеза гармоник, по

формулам (10.31), (10.32) строим F*(/(b). При этом, конечно, должно соблюдаться условие w (0) = 0. Эти формулы можно преобразовать аналогично тому, как это делалось при выражении годографов релейной системы через временные характеристики (см. § 6.2).

Можно также IF* (/со) построить по аналитическим выражениям W*{p) в замкнутой форме, подставив в них р =/со.

Рассмотрим некоторые свойства IF*(/со). Замечая, что

W(jO) = U{0) (10.33)

. W(ja) + W{-joi) = 2U{a), (10.34)

получаем при со = 0

W*{jO) = U*{0)= ii Г(/2тсоо) (10.35)

m=-оо

ИЛИ

, W*(j0)=-U(0) + 2 и(2тщ). (10.36)

Если передаточная функция линейной части имеет полюсы, равные нулю, то слагаемое в правой части (10.36) при со = О обращается в бесконечность, т. е. \(/0) = [/(0) = оо и, следовательно, б этом случае при со = О

W*{iO) = oo. (10.37)

При со = Юо

(/СОо) = 2 Г (/ (2т + 1) СОо) (10.38)

ИЛИ на основании (10.24)

(/соо) - 2 S ((2т + 1) СОо) = С/ Ы- (10.39) Принимая во внимание равенство (6.1-5), Находим

. - - Г*аЧ)==( о) = Ке/(соо). (10.40)

откуда следует, что значение IF* (/со) при со = соо, где cuq -частота периодического режима, пропорционально действительной части годографа релейной системы. ,

Если частота периодического режима соо достаточно высока и I W{j(i)o) I настолько мало, что им можно пренебречь, то тогда всеми слагаемыми IF (/(со + 2тсоо)) при m О в (10.25) можно будет пренебречь, и следовательно.

Г*(/сй) Г(/сй),

(10.41)

т. е. в этом случае IF* (/со) совпадает с частотной характеристикой линейной части системы.

Следовательно, при достаточно высоких частотах периодического режима устойчивость его определяется частотной характеристикой линейной части системы.

Если Шо уменьшать, то будет возрастать роль ранее отброшенных слагаемых. Для того чтобы выяснить влияние соо, рассмотрим частотные характеристики линейной части системы.

W (ju))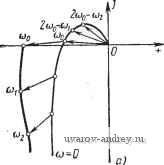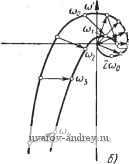

W (joj)

Рис. lO.U. Влияние coj на вид W* (/со).

имеюшие вид, изображенный на рис. 10.11, а, б. Первая из частотных характеристик полностью расположена в П1 и II квадрантах плоскости W (рис. 10.11,а), а вторая при возрастании со, начиная с некоторой частоты со, проходит через I и IV квадранты плоскости W (рис. 10.11,6). Отметим, что вторая из характеристик обычно соответствует линейной части, включающей в себя элементы с распределенными параметрами, с запаздыванием, многоемкостные объекты и т. п. Частотная характеристика IF (/со) (см. рис. 10.11, а) при любом значении со имеет отрицательную вешественную часть. Поэтому, если воспользоваться построением, описанным выше (например, положив в основу формулу (Ш.26) или в общем случае (10.25)), мы получим кривую IF*(/со), которая в III квадранте проходит всегда левее кривой IF (/со).

Обозначим через согр частоту, при которой IF (/со) пересекает действительную ось, т. е, для которой V(corp) = О и W(/corp) =.

= f/(curp). a через com -частоту, при которой l/(cu) становится максимальной.

Тогда для всех частот периодических режимов соо. удовлетворяющих условию

V{(Oo)<0 (10.42)

или при V(ao) > О условию

(сое)<С;(4), (10.43)

№'*(/©) будет расположена в III (и, возможно, в IV) квадранте и пересекать действительную ось один раз при со == соо-

Если же (Во не удовлетворяет неравенствам (10.42) или (10.43), то F*(/(o) может пересекать вещественную ось как при значении со == т, так и при со < о- Однако всегда f/*((Bo)<0.

Иная картина будет для частотной характеристики линейной части системы, изображенной на рис. 10.11,6. Здесь часть частотной характеристики при возрастании со проходив через I и IV квадранты и, следовательно, для этих частот действительная часть ее положительна.

В этом случае f/*(coo) < О лишь при соо < со (рис. 10.11,6). При Юо > со, наоборот, и*{&о) > 0. Если F*(/co) не пересекает отрицательной действительной оси при со < со < coq, то периодический режим (вынужденные колебания) частоты соо будет устойчивым при любой велотине K~.

Определим поведение IF* (/со) при малых значениях со. Из (10.31) легко получить

Г*(/ю)

о

-/со-

(10.44)

т. е. частотная характеристика в этом случае представляет собой дугу окружности радиуса. -\] центром в начале

координат.

Можно показать, что если

- Г*(/со) =

СОо

е>(0)

1\-е

СОо

(10.45) (10.46)

Рассмотрим теперь постоянный для данного периодического режима коэффициент

СОо

(10.47)

Как известно (см. (7.6))

Замечая еще, что (см. (8.2), (8.1), (8.4))

-=Rw

и

Af (л - ф) = (Oof (я - ф) = Юо Re 5 (я - ф), перепишем /С~ в виде

= - Ч') + ( >о)11-

(10.48)

(10.49) (10.50)

(10.51)

В силу условия надлежащего направления переключения (8.5) получаем

/(- = --Ке[5(я-ф) + /(соо)]. (10.52)

Величина /С~ существенно положительна. Она с точностью до постоянного множителя может быть непосредственно опре-

делена по годографу релейной системы. Если относительно точки

ReJ.u)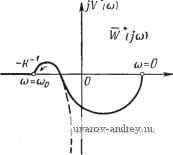

и (cj)

Рис. 10.12. Определение

- /С по Годо-

графу / (ш).

Рис 10.13. Определение поведения

W (/и) вблизи точки Ш = Ш(,.

годографа, соответствующей частоте вынужденных колебаний (Оо, построить кривую (я -ф), то абсциссы точек пересечения ее с прямой -хо и будут равны по абсолютной величине 2fep ,

(рис. 10.12). Это следует непосредственно из анализа условий существования вынужденных колебаний (§ 8.1).

Предположим, что линейная часть системы устойчива или нейтральна и что наибольшей по абсолютной величине абсциссе пересечения кривой W*(ja) с отрицательной частью действительной оси соответствует частота а = щ (рис. 10.13).

Этот случай, как мы видели, всегда имеет место при выполнении условий (10.42) или (10.43).

Тогда условием устойчивости будет

/- <lF*(/©j) = f/4 o). (10.53)

Подставляя сюда значения /<- из (10.52) и t/*(cuo) из (10.40), получим после очевидных преобразований

НеГ(я-ф)=Л^ая-ф)<0. (10.54)

Следовательно, вынужденные колебания частоты о в рассматриваемом случае будут устойчивы для тех значений ф, при которых

НеГ(я -ф) = Л/й(л-ф)<0, (10.55)

т. е. при которых кривая (я -ф) пересекает прямую -ко левее вертикальной прямой, проходящей через центр ff (см. рис. 10.12). В частности, при foiat - ф). = sin(cu - ф) имеем

Re (я - ф) = Л cos (я - ф) = - Л cos ф.

Следовательно, в рассматриваемом случае вынужденные колебания будут устойчивыми при I ф I < 90° и неустойчивыми при 1ф|>90°.

Таким образом, в этом случае устойчивость вынужденных колебаний может быть определена непосредственно по годографу релейной системы /(со).

Если W*{j(i)) пересекает действительную ось левее точки W*(j(x)o) = и*{ао), то неравенство (10.55) является лишь необходимым условием устойчивости. При невыполнении этого неравенства соответствующие вынужденные колебания заведомо неустойчивы.

Рассмотрим теперь еще автоколебания частоты о- В этом случае нужно положить в (10.48) Л = О, а следовательно, и (я -ф) =0.

Тогда

K~=-ReJM (10.56)

и, значит, в силу (10.40) при Re (я - ф) = О

/<-==*(M) = f/*( o). - (10.57)

Следовательно, в этом случае W*{ja) при со - о проходит через точку -/С~ (рис. 10.14), что соответствует границе устойчивости *).

В этом случае уравнение *{р) = 0 имеет чисто мнимый корень р = /соо. Следовательно, этот случай относится к критическим (по Ляпунову). Здесь, однако, справедлива теорема типа теоремы А. А. Андронова и А. А. Витта [1], обобщенной

И. Г. М а л к и н ы м [1], согласно которой для устойчивости автоколебаний необходимо и достаточно, чтобы все остальные корни уравнения W*{p) = ~ О, за исключением корня р == /соо, и.мели бы отрицательные действительные части. Благодаря этому нет необходимости производить дополнительное исследование.

Итак, чтобы применить сформулированный вьпие критерий устойчивости, нужно определить, и.меется ли при со = соо переход W*{ja) через отрезок (-оо,-/(-) или он отсутствует.

Для этой цели исследуем поведение W*(/co) вблизи точки со = СОо (рис. 10.14).

Рассмотрим W*(/co) при со = юо -- Асо (Ло)>0). В случае Дсо С СОо, раскладывая W*(/(coo - Дсои)) в ряд, имеем приближенно: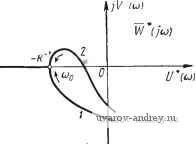

Рис. 10.14. к определению необходимого условия устойчивости автоколебаний.

Производная W (jvi) по со при со = соо равна

Дсо. (10.58)

dU (со)

dV (со)

Ю=(1), ..... -Ю=0)о - co=ti)o

Дифференцируя выражения f/*(co) и 1*(со), определяем (10.29) по со, находим

V (10.59)

dU (со)

dto dV*{co)

dU (со + 2mcO(,)

dV (CO + 2mcOo)

(0=0)

= t;((2m + l)cOo).

Y K((2m+ l)coo)

(10.60;

m=-oo

*) Нетрудно убедиться в том, что при J(t) = всегда имеет периодическое решение (0 = S(<).

; О уравнение в вариациях

Можно показать, что

dV {{2т + 1)щ)

2m + 1 dojo

(10.61)

причем f/((2m -f 1) о) - нечетная функция со, а К'((2/п+1) Юо)- четная функция. Поэтому

2 f;((2m+l)a)o) = 0,

/П=-оо

S K((2 +l,o.) 2i;i!№|±i)a)

т=-оо т=0

Следовательно, по формуле (10.59) получим

(10.62)

dW (/со)

1 dV ((2m+ 1) СОо)

2m + 1 dcoo

Но, С другой стороны, дифференцируя (6.15) по со и полагая со = СОо, имеем

d Im / (соо) 4kp

d&a

1 dK((2m-l)< o)

2m + 1

dV ((2m+l)coo)

2m+ 1

dcoo

Следовательно,

dW (/CO)

rfco

. п d Im / (coo)

dcoo

(10.63) (10.64) (10.65)

Подставляя это значение в (10.58), находим

(/ (СОо - Асо)) - (/Ч) - / щ или, принимая во внимание (10.57),

Г*(/-( о-Дсо)) -i--Z--fAco. (10.66) Отсюда следует, что при

d Im / (соо) dcoo.

> О

(10.67)

кривая W*{ja) подходит к точке {-K~\jO) в П1 квадранте (рис. 10.14, кривая /), а при

dlmJ (сор) dcop

<0

(10.68)

кривая W*{j(i)) подходит к точке (-К~\ /0) во II квадранте (рис. 10.14, кривая 2).

Применяя обычные рассуждения, связанные с обходом при малых значениях со точки р - О на комплексной плоскости р (аналогичные приведенным в § 10.1), приходим к следующему заключению.

Если dal переход W* (/со) при со = о через отрезок (-оо, отсутствует (рис. 10.14, кривая /).

Если rfMp < О' W*(jo)) при со = о совершает половину положительного перехода (рис. 10.14, кривая 2). Знак

dIm/(cop) .опредедяется по поведению годографа /(со) в точках сор

пересечения его с отрицательной частью прямой -щ, т. е. в точках, соответствующих частоте автоколебаний. Из рис. 10.15 следует, что если характеристика /(со) при возрастании со пересекает прямую -в точке со = СОо снизу d Im / (сор)

dcop

Рис. 10.15. Определение необходимого условия устойчивости автоколебаний по годографу / (со).

> О, если

же характеристика /(со) пересекает прямую -Но сверху

с Im / (сор)

<0.

вниз, то --

Если линейная часть устойчива или нейтральна (а далее мы это всегда будем предполагать, если не оговорено противное) и отсутствует пересечение IF*(/со) отрезка (-оо,-/(-) при а ф Ф СОо, то тогда на основании ранее сформулированного критерия устойчивости заключаем, что автоколебания частоты соо устойчивы в том случае, когда

> 0. (10.69)

Если отрезок (-оо, -/С~) пересекается кривой IF* (/со) при (в СОо, условие (10.69) является лишь необходимым условием устойчивости автоколебаний. При невыполнении неравенства

(10.69) автоколебания будут неустойчивыми*). При желании использовать алгебраические критерии устойчивости, нужно обратиться к уравнению (10.11). В данном случае

2fep

W*(p) = 0,

(10.70)

где W*{p) определяется формулой (9.106), или, в общем случае, формулой (9.112).

Находя числитель 4*{р), приравнивая его нулю и полагая

и = е , получим характеристическое уравнение относительно и. К этому характеристическому уравнению применяются алгебраические критерии устойчивости.

§ 10.4. Релейные системы с зоной нечувствительности

Рассмотрим теперь методику исследования устойчивости периодических режимов в релейных системах с зоной нечувствительности. В этом случае W*{p) выражается не просто через W*(p), а через комбинацию W*{p) и W*{p,±\) (см. формулу (9.86)).

Подставляя в формулу (9.86) р = /со, запишем ее в следующем виде:

W*Ua>) = KrKyWAi(i>), (10.71)

где

О ) = 1+ кг] (/со) +

+ (/CD) - Г' (/со, Y) (/со, - у):

(10.72)

(10.73)

r(/co)=f-ir(/co), Г'(/CO. ±Y) = -r*(/a), ±у).

(10.74)

*) Это условие было приведено в книге автора [5]. Тот факт, что это условие в общем случае является только необходимым, иным путем был получен П. В. Б р о м б е р г о м [Ц и независимо от него Ю. И. Неймарком [I].

Вопрос об устойчивости периодического режима частоты о решается согласно сформулированному в § 10.1 частотному критерию устойчивости подсчетом числа и знаков переходов кривой W(/cu) через отрезок (- оо, - КуКГ\ Кривые W*{j(i), ±у) могут быть построены теми же способами, что и кривая IF*(/со), с той лишь разницей, что теперь при использовании частотной характеристики вместо

W{M = U((i,) + jV{(i>) (10.75)

нужно рассматривать

W (/со) = (f/ (со) cos у + F (ю) sin coy 1 -f

-f / (± f/ (со)sin (i>y~+V(Ю)coscoy-). (10.76)

При построении W* (/со, ± у) по импульсной характеристике

wk-j нужно заменить на йу ( ± у), Очевидно, что

W*{ja, ±у) можно также вычислить по их аналитическим выражениям в замкнутой форме, приведенным в § 9.8. Необходимое

условие устойчивости имеет вид (рис. 10.16)

-KrKyKWiJ), (10.77)

где W*(/cu) определяется выражением (10.72).

Найдем величины, входящие в это неравенство. При р - / о из формулы (9.51.) получаем

ГЧ/ о. у) =

2 e/(2 +)v>xuj(/(2m+1) )

(10.78)

или, принимая во внимание (10.75), при со = о:

Рис. 10.16. Необходимое условие устойчивости вынужденных колебаний.

R*(M.y) = 2 2 [f/((2m-l)coo)cos(2m-1)уя-

- V ((2m - 1) COo) sin (2m - 1) уя]. (10.79)

Сомоставляя это выражение с выражением /, (со) (6.61), 1у{<£>) (6.62) и /(со),(6.18), находим

. 1(/ о, -Y) = [Re/(coo)-2Re/,(coo)]

(10.80)