контуром L, отсутствовали нули Ч*(р), т. е. корни уравнения if*(p) ==0. Полагая в (10.2) н = О, находим условие устойчивости периодического режима в виде

Д£агеЧ*(р) = 2яп, (10.3)

где п - число основных полюсов Ч'*(р), лежащих в правой части комплексной плоскости р, т. е. число правых полюсов.

Отметим, что основные полюсы Ч'*(р) совпадают с полюсами W*(p), а значит, и с полюсами передаточных функций линейных

Рис. 10.1. Контур L. К применению принципа аргумента.

0)<0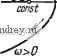

Рис. 10.2. Кривая (/и).

частей W{p), Whm{p)- Поэтому число основных полюсов *F*(p), лежащих в правой части плоскости р, можно определить непосредственно по W(p),. Whmip)-

Когда р изменяется вдоль мнимой оси от -/соо до /соо (отрезок Li), Ф*(р) будет описывать некоторую замкнутую кривую

Т*(/сй)=1-f W (/cu). (10.4)

Так как Ч'*(-/юо) = Ч'*(/<во) вследствие периодичности F*(p), то эта кривая будет пересекать действительную ось по крайней мере при со = О и со = ©о (см. рис. 10.2).

При изменении р вдоль прямой /.2(р = o-f /©о) от о = О до о = оо функция W* (р) будет изменяться вдоль действительной оси от W*{jao) (см. рис. 10.2) до значения

lim W* (а + /соо) = const. (10.5)

Это же значение *F*(p) будет иметь при изменении вдоль бесконечно удаленного отрезка прямой 2(0 = оо). Наконец, при изменении р вдоль прямой Ьз{р = а - /соо) от а = оо до а = О вследствие периодичности

Ч'( 7-/ )о) = *(а + /Ч)-

Следовательно, Ч'*{р) будет изменяться вдоль действительной оси от значения (10.5) до значения Ч^*(/©о) в направлении, противоположном предыдущему.

Таким образом, для подсчета изменения аргумента .LaтgW*{p) при изменении р вдоль замкнутого контура L ветви кривой W*{p), соответствующие изменению р вдоль L2, Ls, Ц, не играют роли. Изменение аргумента Ai. arg Ч* * (р) целиком определяется кривой Ч'*(/(й), получаемой при изменении со в интервале -т < со соо, т. е.

Aiarg4f*(p) = A arg Ч^(/ >) (Ю-б)

(-(йо<(й<СО,)

Условие устойчивости представится в виде

Д arg Ч^*(/со) = 2яп. (10.7)

(-()о<Ь)<Ь)о)

Так как Ч^*(/со) и Ч'*(-/со) -комплексно сопряженные функции, графики которых симметричны относительно действительной оси, то пря изменении со от нуля до ио изменение аргумента уменьшится вдвое, и окончательно условие устойчивости запишется в виде

Д arg Ч'*(/со) = яп. (10.8)

(0<со<(йо)

В частности, если линейная часть системы устойчива, то п = О, и условие устойчивости примет вид

Д arg Ч^*(/со)==0. (10.9)

(0<со<(0о)

Если изобразить кривую W* (/со) для соо со О, то Ч^*(/со) представит собой вектор, проведенный из точки (-1, /0) к кривой

1Т*(/сй) (рис. 10.3). По расположению точки (-1,/0) относительно W*(j(i)) можно судить об изменении аргумента Ч^*Цса), а значит, и об устойчивости периодического режима.

Назовем переход W*{ja) (с возрастанием со от нуля до ©о) через отрезок действительной оси (-оо, -1) с верхней полуплоскости в нижнюю положительным (а), а с нижней полуплоскости в верхнюю - отрицательным (б) (см. рис. 10.3). Если значение W*{ja) при со = = 0 или со = СОо находится на отрезке (-оо,-1), то при этих значениях будем считать, что W*(/co) совершает половину перехода.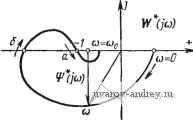

W*(jo)

Рис. 10.3. Кривая W* (/со): о)-положитель иый переход, б) -отрицательный переход.

Изменение аргумента 4*(jca) при изменении со от нуля до соо будет равно нулю, если число переходов W*(/co) (при возрастании со) через отрезок действительной оси (-оо, -1) с верхней полуплоскости в нижнюю и с нижней полуплоскости в верхнюю равно друг другу.

Изменение аргумента Ч'*(/со) будет равно ±пя, если разность

между числом этих переходов равна ± у.

Таким образом, критерий устойчивости вынужденных колебаний частоты СОо можно сформулировать следующим образом.

Периодический режим частоты соо будет устойчивым, если разность между числом положительных и отрицательных переходов W*(;co) через отрезок (-оо, -1) при возрастании со от

нуля до соо равна , где п - число правых полюсов передаточной функции линейной части.

В любом другом случае периодический режим частоты соо будет неустойчивым.

В наиболее распространенных случаях, если линейная часть устойчива, периодический режим частоты соо будет устойчивым, если разность между положительными и отрицательными переходами W*(/co) отрезка (-оо, -1) равна нулю, и неустойчивым в любом другом случае.

Предположим теперь, что функция *{р) (или, что то же, W*\p)) имеет полюсы на мнимой оси (рис. 10.4). В точках, соответствующих этим полюсам, W*(/Q) обра- р„е. ,о.4. контур i пр пл ч„ п ЩаеТСЯ в бесконечность. Выберем контуре корней уравнения Ф* (р)=0.

на комплексной плоскости р замкнутый контур и, отличающийся от контура L тем, что бесконечно малые отрезки мнимой оси, внутри которых лежат полюсы функций W*{p) (или, что то же, полюсы W*{p)) заменены полуокружностями бесконечно малого радиуса, лежащими в правой части комплексной плоскости (рис. 10.4). Если изменять р вдоль этого контура в направлении, указанном стрелками, то на основании принципа аргумента мы получим формулировку критерия устойчивости, установленную выше. В этом случае при изменении вдоль бесконечно малых полуокружностей вектор *(У(й) (а значит, и llF*(/co)) будет скользить по соответствующей дуге бесконечно большого радиуса, центральный угол для

которой равен я--, где п' - кратность полюсов, лежащих на

мнимой оси.

практически наиболее часто встречается случай одного или двух полюсов, лежащих в начале координат.

Таким образом, в этих случаях применим сформулированный Bbuue критерий устойчивости, только при построении годографа частотной характеристики следует дополнить ее дугами бесконечно большого радиуса, направление обхода которых противоположно направлению обхода соответствующей полуокружности бесконечно малого радиуса. На рис. 10.5 приведены кривые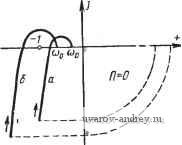

Рис. 10.5. Кривые W* (/га) при п'=1, соответствующие устойчивому (о) и неустойчивому (б) периодическому режиму.

Рис. 10.6.

Нормированная

W(ja), соответствующие (при п = 0) устойчивому (кривая а) и неустойчивому (кривая б) периодическим режимам частоты соо-

При доказательстве критерия устойчивости предполагалось, что на границах L2, полосы нет нулей и полюсов функции W*{p). Если это предположение не оправдывается, то, обходя эти нули и полюсы полуокружностями бесконечно малого радиуса, как показано пунктиром на рис. 10.4, получим несколько деформированные, но по-прежнему совпадающие ветви функции Ч'*(р), которые, как и ранее, не влияют на изменение аргумента Ч'*(/(в). Поэтому прежние формулировки критерия устойчивости остаются в силе и в этом случае.

Кривую W*(/co) можно рассматривать как частотную характеристику разомкнутой импульсной системы. Она получается заменой р на /со в функции W*(p).

Часто вместо кривой W*(/co) целесообразно рассматривать нормированную кривую W*(/co), определяемую из соотношения

W*ih) = KW*(h), (10.10)

где К-постоянная величина, не зависящая от со. Нормированная кривая W*(/co) отличается от й^*(/со) лишь масштабом. Если графически изображать нормированную кривую W*{ja), то точке -1 будет соответствовать точка -K~ (рис. 10.6), и в

формулировке частотного критерия устойчивости следует отрезок (-оо, -О заменить на отрезок (-оо, /С ).

Входящие Б W*{p) функции W*(p), W*(p, ±у) при р =/ю можно вычислить, применяя в зависимости от исходных данных ту или иную их форму.

§ 10.2. Алгебраический критерий устойчивости

Если функции W*{p,±y) найдены в замкнутой форме, то уравнение

F*(P)=1 +W {p) = 0

(10.11)

определяет собой в явном виде дробно-рациональную функцию

от е \или от е

2л

. Обозначая

\или и = е ,

можно это уравнение представить в виде

F(p) = F,( ) = 0.

(10.12)

(10.13)

Подстановка -W0 < Im р S

(10.12) преобразует левую часть полосы Шо (рис. 10.7, а) в круг единичного радиуса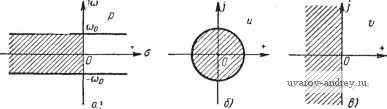

Рис. 10.7. Преобразование полосы (о) в круг (6) и круга (6) в полуплоскость (в).

(рис. 10.7, б). Следовательно, для того чтобы периодический режим был устойчив, необходимо и достаточно, чтобы все корни уравнения (10.13) лежали внутри круга единичного радиуса.

Эта задача может быть сведена к известной задаче определения условий, при которых корни уравнения (10.13) лежали бы все в левой части комплексной плоскости, т. е. к задаче Гурвица. Для этого воспользуемся новой заменой переменной

v + i

(10.14)

которая устанавливает взаимно однозначное соответствие между кругом радиуса 1 и левой частью комплексной плоскости р

(рис. 10.7,в). Тогда к числителю уравнения r(-) = 42(t) = 0

(10.15)

можно применить алгебраические критерии Гурвица или Рауса, использующиеся в теории непрерывного регулирования.

Если коэффициенты уравнения (10.15) определены численно, то наиболее удобно применять критерий устойчивости в форме, данной Раусом *).

Предполо.жим, что числитель уравнения Wi{u) = 0 имеет вид

goU +g,U ++ ... +gniU+gn = 0. (10.16)

Тогда, применяя алгебраический критерий устойчивости, можно получить следующие неравенства, обеспечивающие устойчивость периодического режима**):

для п=1

go--gi>0;

(10.17)

для п = 2

для п = 3

для п - 4

go-bgi + g2> о, go-gi + g2> о, go-g2>0;

go + gl + g2 + g3> 0, go- gl-h g2 - g3<

go ig2 - go) + (ёз - go) g3 > 0.

igo + g3) - gi - go>0;

(10.18)

(10.19)

(10.20)

g0+ gl + g2+ g3 + gi> 0, go- gl + g2 - g3 + gi> 0, (go - gi) [gl (g3 - gl) - (g2 - go- g4) (go - gi)] +

+ go{e3-gi)>0, 4(о-Ы + 2(ёГз-ёГ1)>С. 4(ёГо-ёГ4)-2(ёГз-ёГ1)>0.

*) Отметим, что существует и прямое решение этой задачи без сведения ее. к задаче Гурвица, которое читатель может найти в работах М. Мар-д е н а [1], Н. Н. Меймана [1].

**) Подробный вывод этих неравенств можно найти в книгах Р. О л ь-денбурга и Г. Сарториуса [1], П. В. Бромберга [1], [2], автора [16] В этой последней работе приводится также критерий устойчивости аналогичный критерию устойчивости Михайлова.

в простейших случаях алгебраический критерий устойчивости позволяет найти условия устойчивости периодических режимов Б аналитической форме. В том случае, когда степень уравнения становится больше четырех, число условий возрастает, а вместе с этим возрастает и громоздкость вычислений.

§ 10.3. Релейные системы без зоны нечувствительности

Прежде чем переходить к исследованию устойчивости перио дических режимов в конкретных релейных автоматических системах, остановимся на методике применения частотного критерия устойчивости и рассмотрении при помощи этого критерия некоторых общих свойств. Для симметричного периодического режима Б релейных системах без зоны нечувствительности

Обозначим

(10.21)

(10.22)

Тогда

\riJ(i))=KW (/со).

(10.23)

(10.24)

Исследование устойчивости периодических режимов согласно частотному критерию устойчивости сводится к построению 1*(/сй). Полагая в (9.33) р = /со, найдем

W4h)= 2 Г(/(со-Ь2тсоо)).

(10.25)

откуда следует, что IF* (/со) можно построить по частотной характеристике линейной части системы WQa). Для этой цели, задавшись значением со = соь отметим на W (/co) (дополненной симметричной кривой для значений со < 0) точки

СО] + 2соо, 1 - 2юо,

©1 + 4юо, ... со, -4coi,

где Юо - частота периодического режима, а coi - любая частота, меньи1ая coq. Геометрическая сумма векторов, проведенных из

начала координат к этим точкам (рис. 10.8,а), согласно (10.24) и определяет *(/со) при со = coi.

Задаваясь иными значениями со в интервале О со соо, аналогичным образом можно найти И?*(/со) при интересующих нас значениях со. Векторы 1(/(со + 2тсоо)) можно складывать либо геометрически либо суммировать отдельно действительные и мнимые части.

W (jco)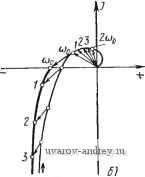

Рис. 10.8. к построению W* (/(0) no W (/CO).

Так как с ростом со модуль частотной характеристики линейной части I IF (/со) I обычно стремится к нулю, то при построении F*(/co) по выражению (10.25) в последнем можно обычно ограничиться небольшим числом слагаемых. Число этих слагаемых легко выясняется при построении. Часто это число можно принять равным двум; тогда

W (/со) W (/со) + W (/ (со - 2соо)).

(10.26)

В этом случае построение W*(/co) особенно просто. Из каждой точки coi < СОо, как из начала координат, проводится вектор \F(/(cot -2соо)), сопряженный вектору \F(/(2coo -Юг)), как по казано на рис. 10.8, б. Соединяя концы этих векторов, получаем Г* (/со).

Аналогичным образом можно, очевидно, при необходимости учесть последующие слагаемые.

Описанный способ построения 1*(/со) очень удобен при качественном исследовании вида W*(ja). Для фактического построения IF* (/со) более удобно применять способ, основанный на сложении соответствующим образом смещенных вещественных и мнимых частей частотной характеристики, линейной части

системы:

Г(/(о) = (а)) + /Т(и).

Обозначая аналогично

W*(Jw)=U{(i>) + jV*{a)

(10.27) (10.28)

и подставляя W*{j(ii) и 1(/со) в (10.25), получаем после отделения вещественных и мнимых частей

Г(со)= 2 У((о-Ь2тсйо).

(10.29)

Отсюда следует, что вещественная и мнимая части IF* (/со) равны соответственно сумме вещественных и мнимых частей частотных характеристик линейной части системы

1Г(/((о + 2тсоо)).

(10.30)

где т = 0, ±1, ±2, ...

Для построения U*(a) и V*(co) изобразим графически вещественную и мнимую части частотной характеристики системы

Рис. 10.9. Частотная характеристика линейиой части \ (/о))(а), действительная С/ (со) и

мнимая V (СО) части ее (б).

(рис. 10.9,6), которые соответствуют частотной характеристике (рис. 10.9, й). Затем эти характеристики сместим вдоль оси частот на ±2тсоо (рис. 10.10,а и б). Производя суммирование для каждого значения со в интервале от нуля до соо, получаем и V*(co).

Построенные таким образом t/*(cu) и У*(со) изображены на рис, 10.10,а жирной кривой в интервале -coq < со < соо. В остальных интервалах (У* (со) и 1/*(ю) изменяются периодически.

По найденным значениям и*(а) и У* (со) находим 1Г*(/со) (рис. 10.10,6)).

Рис. 10.10. Построение U* (со) (a), К* (со) (6). Вид W* (/со) (s).

Можно также построить

Г(/со) = -Г*(/а))

по импульсной характеристике. Для этого положим в выражении (9.92) у = 0 и р==/т и подставим его в (10.23):

W*(/co) = U7-(/co, 0) = V ,--,(/,). (10.31)

Отделяя действительную и мнимую части, получим

fe=i