где s - целое число, так как замена р на р + 2/scuo не изменяет правых частей (9.26) и (9.27). S*(p) является аналитической функцией в полосе -юо < Im р юо (рис. 9.8), за исключением конечного числа точек - полюсов р = р^, которые, как это видно из (9.27), отличаются от полюсов Е(р) только мнимыми частями. Если два различных полюса отличаются между собой на ±2/5(00. то в Е*(р) они будут соответствовать одному полюсу.

Подставив S(p) из уравнения (9.25) в (9.27), получим

S* (р) = S + -

о

\ Шо / m=-оо

XE*(p + 2/m(Oo). (9.30)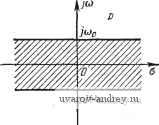

Рис. 9.8. Плоскость р и полоса -Ио < Im р < coj.

Учитывая периодичность S*(p) (9.29), запишем это уравнение в виде

где в соответствии с соотношением (9.27) обозначено:

/н(р)=-2и(р + Утсоо)

(9.31)

(9.32)

WAp) = Yw(p-i-2m). (9.33)

m=-оо

При наличии скачка ш(0) ф О вместо (9.33) будем иметь

г Чр) = - + -5- 2 + 2/ о). (9.33)

т=!-оо

что представляет собой левое значение передаточной функции разомкнутой импульсной системы.

Разрешая уравнение (9.31) относительно изображения S*(p), получаем

S*(P) =-----П(р) (9.34)

или

где

ВЧр)=Г{р)К(р),

кЧр)=-

(9.35) (9.36)

К*(р) представляет собой передаточную функцию замкнутой импульсной автоматической системы. Выражение

W4p)-=

( Ио )

(9.37)

можно рассматривать как передаточную функцию соответствующей разомкнутой импульсной автоматической системы.

Ф,(т1(!.б)

(4 i, ti t -Xq о Xq

Ф^(ха1:6)

t, f, t, t2 t, X

Рис 9.9. Зависимости (jE (<); a) -ш и Фд (jE (0; о) -С).

Уравнение в вариациях определяет изображение последовательности импульсивных функций, модулированных величиной g(0, т. е. изображение дискретных значений g(0. Нетрудно, однако, найти изображение самой величины (/). Для этой нелн подставим значение S*(p) из (9.35) в (9.25). Тогда получим уравнение относительно S(p):

S (Р) = f. (р)--rfer- (Р) (Р) (р). (9.38)

i-(iL)

Уравнения (9.34) и (9.38) и являются для рассматриваемого случая релейной характеристики без зоны нечувствительности различными формами уравнений в вариациях,

Эти уравнения остаются справедливыми и для релейного элемента, обладающего гистерезисом (>со¥=0). В этом случае Ф2(х(ty, о), как видно из рис. 9.9, соответствует рассмотренной выше последовательности импульсивных функций, но смещенной по времени на постоянную величину, различную при положительном и отрицательном гистерезисе.

Так как выбор начального момента времени произволен, то это смещение не оказывает влияния на вид уравнения в вариациях. Таким образом, уравнения в вариациях (9.34) и (9.38) справедливы и при наличии гистерезиса любого знака.

§ 9.4. Уравнение в вариациях при иа.!1ичии зоны нечувствительности

При наличии зоны нечувствительности, как видно из рис. 9Л,г,2 и (9.13)

Ф4 [х it)) = ftp [б (х it) - ко) -f б (х it) + коМ. , Обозначим, как и ранее (см. § 3.4) через tk корни уравнения xit) - i- 1)ко = 0 а через tk - корни уравнения

х(0 + (- 1)ко = 0. Тогда корнями уравнения

xit) - no = 0

будут

to, t\, tz, tz, ... , 4m, fem+1, ... , (9.39)

a корнями уравнения

х(0 + Ко = 0

будут

t\, ts, ta, ti, ... , 2m+l. 4m+ 2, ... (9.39)

При периодическом режиме, как было указано в § 5.3,

f-W + - = ( + Y)-- (9.40)

- Для определения dixit) - Kq) И б(х(0 + Ко) применим формулу (9.17), подставляя в нее вначале значения fe и 4n+i (9.39), а затем 4т+i и 4т+ 2 (9.39). Замечая, что tk и tk+i

даются выражениями (9.40) и учитывая периодичность х (t), получаем

б{хЦ)-щ)-

* ( Ио )

26(-(2m+Y)i)

б(х(0 + Ко)

( о ) +

2б(-(2т + 1)-) +

2б(-(2т + 1+у)-)

Подставляя эти значения в Oi{x{t)) (9.13), находим *Р

Ф4((Ф = -

( СОо )

S6(-( + y)-t). (9-41)

X Y-

4((0) соответствует сумме двух последовательностей импульсивных функций (дельтатфункций). Период повторения

этих последовательностей - один и тот же и равен - . Интен-

сивность или площадь импульсивных функций первой после-довательности равна --,-\-. а второй последовательности

-, Вторая последовательность смещена относигель-

но первой на постоянное время, равное y

На рис. 9.10 приведена геометрическая интерпретация преобразования x{t) -В указанные последовательности импульсивных функций при помощи, характеристики Oi{x(t)). Принимая

во внимание (9.41), запишем уравнение в вариациях (9.9) в виде

Lm)}L[fAt)]-W{p)L

. (9.42)

-( n\

Wo)

Применим соотношение (9.22), полагая в нем ta = k ~ и

ф;(£ф1

Рис. 9.10. Зависимость (Jc (fl).

a~{k-\-y)~. Тогда (9.42) можно переписать иначе:

fe=0

-p(ft + v)- / N

2. 5(( + V))

Обозначая

B>,v) = i;r l(№ + v)i)

oo я

. (9.43)

(9.44)

fe=0

и используя прежнее обозначение (9.26), приведем полученное выше уравнение к виду

S(p) = F (p)-W(p)

PY -

( Юо ) о)

S*(p,Y)

. (9.45)

Это уравнение соответствует более сложной, чем раньше, импульсной системе (рис. 9.11), состоящей из линейной части с передаточной функцией W{p), двух импульсных элементов и двух усилителей.

~-*ф-т*

Рис. 9.П. Линейная импульсная автоматическая система, соответствующая уравнению

в вариациях (9.45).

Период повторения импульсных элементов один и тот же - -, но работа второго импульсного элемента происходит с за-

паздыванием относительно первого на постоянную величину

Y , т. е. импульсные элементы работают синхронно, но не

синфазно. Коэффициенты усиления усилителей равны соответственно

Входная величина линейной части, характеризуемой передаточной функцией W{p), представляет собой последовательность импульсов (рис. 9.10), которая промодулирована отклоне-. нием l(t).

Преобразуем уравнение (9.45) с целью определить в данном случае изображения Е*(р), Н*(р, у) и Н(р). Для этого наряду с соотношением (9.27) воспользуемся соотношением более

общего вида

Е.(р + 2тщ), (9.46)

которое обращается в (9.27) при v = 0. Вывод этого соотношения приведен в Приложении 2. Отметим, что при у = 1 (что соответствует ко = О, т. е. отсутствию зоны нечувствительности), из (9.46) получаем

(р, 1) = f - / 2 (р + 2/тшо) = е Е' (р) (9.47)

и, следовательно, уравнение (9.45) при у = 1 обращается в уравнение (9.38).

Подставляя Е(р) из уравнения (9.45) в правые части соотношений (9.27), (9.46) и учитывая периодичность Е*(р) и Е*(р, у), получим два уравнения относительно этих изображений:

Е'(р) = Гн(р)-

*Р .W , чо./ \ kp

~ hi)

Е'(р, у) = П(р, y)-

R*(p,-y)3(p. y).

w (p)e*(p, y).

(9.48)

или, в упорядоченной форме.

s*(p) +

. (р, - y) s (р, у) = f;; (р).

(9.49)

в этих уравнениях Рн{р) и W*{p) определяются уравнениями (9.32), (9.33), что же касается

Flip, Y) и Wip, ±у), то они равны соответственно

(Р- Y) = S е F. (р + 2/тсоо). (9.50)

W4p, ±У)- S е

.rp v-,p 2/mcOo). (9.51)

При у = 0 и выполнении условия типа (9.28) выражения (9.50), (9.51) переходят в (9.32), (9.33).

Решая систему двух линейных уравнений (9.49), находим

Fnip)-

W{p,-y)Fl{p, у)

E(p, Y)=

V Wo /

Wip, y)Flip) +

Wip)

Flip, Y)

(9.52)

Здесь *ip) есть главный определитель системы

Г(р) =

W* (р)

х- -]

(р, - Y)

. (9.53)

W (р)

в раскрытом виде Г *Р

W(P) +

(р) - W (р, у) W ip, ~ y)l (9.54)

Вводя передаточные функции

Ки (р) =

/СГ2(р)

w4p)

Ч'- (р)

/2l(p) = --F

/22(Р) = -5ГГ

* ((flo)

W (p, у), Wip)

(9.55)

запишем уравнения в вариациях относительно З'(р) и S*(p, у):

(р) = Kh (р) К (Р) + Kh (р) /-Г, (р, Y), 1

3* (Р. Y) = Kh (р) (р) + Kh (р) (р, Y). / -

Уравнение в вариациях относительно 3(р) можно получить после подстановки S*(p) и Н*(р, Y) из (9.56) в правую часть уравнения (9.45):

S(p) = F (p)--W(p)

-КЬ{р) +

к Y-

Kl2{p) +

к~ Y - У щ I

Khip) Flip)-

F.(p,y). (9.57)

Найденные выше уравнения в вариациях (9.56), (9.57), остаются справедливыми и для релейного элемента, в котором наряду

с зоной нечувствительности имеется гистерезис, т. е. для релейного элемента с коэффициентом возврата Л, отличным от единицы. В этом случае, как видно из рис. 9.12, рассмотренная

t tl if

Рис. 9.12. Зависимости Фд (JE (f); о) -a) и Og (jc (f); a) -6).

последовательность импульсивных функций смещается по времени на постоянную величину, что не оказывает влияния на вид уравнений в вариациях.

§ i9.5. Уравнение в вариациях для сложных режимов

Рассмотрим релейную автоматическую систему без зоны нечувствительности и гистерезиса, в которой имеет место сложный периодический режим.

Предположим вначале, что внутри полупериодаизменяет знак нечетное число s = 2m- 1 > 1 раз, и ( + ) -

= - y{t). В этом случае Ф|(х(/)) будет определять собой S = 2т-1 последовательностей импульсивных функций с одним и тем же периодом повторения - (рис. 9.13). Каждая из

этих последовательностей смещена на величину у,--- (г == 1,

2, .... S-I) и интенсивность или площадь импульсивных функций в i-H последовательности равна соответственно 2*п

( \

Для определения уравнений в вариациях, связывающих Е(р) и E*(p,Yi), воспользуемся схемой эквивалентной импул.ьс-