Глава IX

УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ РЕЖИМОВ В РЕЛЕЙНЫХ АВТОМАТИЧЕСКИХ СИСТЕМАХ

§ 9.1. Понятие устойчивости периодических режимов

Периодические режимы были подробно рассмотрены в предыдущих главах. К этим режимам относятся автоколебания и вынужденные колебания, причем последние могут быть как основной, вынуждающей частоты, так и субгармоническими. Периодические режимы могут физически наблюдаться в системах лишь в том случае, когда они устойчивы. Поэтому после установления существования возможных периодических режимов (автоколебаний или вынужденных колебаний) важное значение приобретает выяснение устойчивости этих режимов.

Исследование устойчивости позволяет из возможных периодических режимов выбрать физически реализуемые, т. е. те режимы, которые будут иметь место в действительности.

Пусть x{t) определяет собой периодический режим. Будем судить об устойчивости этого периодического режима по поведению состояния релейной автоматической системы, вызванного достаточно малыми возмущениями, т. е. по поведению близких к периодическому режиму соседних непериодических режимов

x{t) = x{t) + m. (9.1)

Здесь !(/)-отклонение от стационарного периодического режима, вызываемое достаточно малым возмущением.

Если при достаточно малом возмущении отклонение после устранения этого возмущения с ростом времени стремится к нулю, т. е.

lim(/) = 0, (9.2)

fo исследуемый периодический режим асимптотически устойчив. В этом случае с ростом времени все ближайшие непериодические режимы стремятся к рассматриваемому периодическому режиму.

Если же при указанных выше условиях с ростом времени 11()1 неограниченно возрастает, то исследуемый периодический режим неустойчив.

Для исследования устойчивости периодических режимов нужно составить уравнение движения относительно отклонений, которое получается после замены в общих уравнениях x{t) его значением из (9.1), и отбросить в этих уравнениях все члены, содержащие степени g(/) выше первой.

Полученное таким образом линейное уравнение, называемое уравнением первого приближения или уравнением в вариациях, в рассматриваемом случае имеет периодические коэффициенты.

Если решение уравнения в вариациях (t) с течением времени стремится к нулю, то исследуемый периодический режим устойчив, причем устойчив асимптотически, каковы бы ни были отброшенные в исходном уравнении нелинейные члены. В случае неограниченного возрастания () исследуемый периодический режим неустойчив.

Если же решение уравнения в вариациях (0 не стремится с течением рремени к нулю, но ограничено по абсолютной величине, то, вообще говоря, нельзя сделать вывод об устойчивости или неустойчивости исследуемого режима без рассмотрения отброшенных ранее нелинейных членов. Этот случай относится к критическому.

Однако в интересующих нас задачах благодаря теореме А А. Андронова и А. А. Витта [1] это затруднение исключается, и уравнение в вариациях дает ответ на вопрос об устойчивости и в этом критическом случае*).

Для исследования устойчивости периодических режимов в релейных автоматических системах воспользуемся идеологией классического метода Ляпунова.

Заметим, что метод Ляпунова применим, вообще говоря, к уравнениям с непрерывными нелинейными функциями, тогда как релейные системы описываются уравнением с разрывными функциями. Поэтому строгое рассмотрение требует, чтобы все рассуждения были проведены относительно непрерывных функций, аппроксимирующих с любой степенью точности данную разрывную функцию, а затем уже необходимо совершить переход к разрывной функции как к пределу.

Этот строгий, но весьма громоздкий путь в конечном итоге приводит к тем же результатам, что и непосредственное применение метода Ляпунова к уравнениям с разрывными характеристиками, если использовать широко применяющиеся в физике и технике так называемые дельта-функции.

Далее мы будем следовать второму пути, который достаточно нагляден с физической точки зрения.

*) Более общая форма этой теоремы была доказана И. Г. Малки-н ы м [1].

§ 9.2. Уравнения в вариациях

Предположим, что

x{t)f{t)-zit) (9.3)

соответствует периодическому режиму частоты шо- Для исследования устойчивости его составим уравнение в вариациях. Величина x{t), определяющая периодический режим, удовлетворяет уравнению

L {X Ш = L {f it)} -Wip)L {Ф [х it); а)}. (9.4)

Предположим теперь, что в некоторый момент времени, например, / = О, в релейной системе в силу некоторых причин (например, изменения начальных условий) возникло мало£ возмущение. Это возмущение нарушит периодический режим, и теперь x{t) будет непериодической величиной, определяемой соотношением (9.1).

Приводя согласно правилу, изложенному в § 2.4, возмущение ко входу релейного элемента и обозначая его через fnit), уравнение релейной системы (2.96) можно записать после замены x{t) его значением из (9.1) в виде

L {X it) + I (t)} = L {U [t)} ~W(p)L {Ф {X it) + I it); a)}. (9.5)

Вычитая из уравнения (9.5) уравнение периодического режима (9.4), находим уравнение относительно отклонения () от рассматриваемого периодического режима:

L {I (/)} = L {h (t)} -W{p)L {Ф [х (t) + g it); а)-Ф(х (t); a)}. (9.6)

Это уравнение нелинейно относительно изображения (t). Характеристика релейного элемента Ф(-) может принимать лишь значения ±kp или О Поэтому 0(x(t);a) представляет собой последовательность импульсов постоянной высоты ftp, длительности Y~ (О < 1) и чередующихся знаков.

о

функция 0{x(t) -{-{t);a) представляет собой также последовательность импульсов постоянной высоты ftp и чередующихся знаков, но уже переменной длительности, зависящей от КО.

Разность этих двух функций

Ф(хit) + Uty <У)-Ф(xit); о) (9.7)

соответствует некоторой последовательности импульсов постоянной высоты и длительности, зависящей от (0.

Для релейного элемента без зоны нечувствительности эта последовательность может, например, иметь вид, показанный Ра рис. 9.1.

Разделив и умножив разность (9.7) на %{t), уравнение (9.6) можно переписать в следующем виде:

L{W)=-L{m}-Wip)L{ Ф((0 + и0.а)-Ф((0=а) .() д^

Для малых значений (0 получаем

L { (/)} = L {f (t)} -W(p)L {Ф' {X (t); а) I (t)}.

(9.9)

В этом уравнении удержаны лишь члены, линейные относительно %(t), а Ф'(-) означает производную характеристики релейного элемента по ее аргументу, т. е. по входной величине релейного элемента х.

Ф(хП)*шЫ)-Ф(хт:б)

Рис. 9.1. Изменение разности Ф(ли + 1(0: о)-Ф(х((): а).

Рнс. 9.2. Характеристика релейного еле менга (а) и его производная (б) как предел характеристик элемента с насыщением.

Уравнение (9.9) представляет собой линейное уравнение с периодическими коэффициентами, так как, помимо изображения искомой переменной (0, оно содержит и изображение произведения искомой переменной (0 на периодическую функцию

Как уже было указано выше, задача исследования устойчивости периодических режимов в релейной автоматической системе сводится к исследованию поведения решений этого уравнения с периодическими коэффициентами.

В общем случае при произвольной форме Ф(д;; а) исследо--вание решений уравнений с периодическими коэффициентами наталкивается на непреодолимые трудности. Однако для релейных автоматических систем в силу специфического вида характеристики Ф (х; о) оказывается возможным сравнительно про-

стьш путем произвести исследование устойчивости периодических режимов.

Рассмотрим вначале простейшую характеристику релейного элемента (рис. 9.2,а). Эту характеристику можно считать предельным случаем семейства характеристик с линейным участ-

ком при неограниченном возрастании наклона линейного

участка вследствие стремления ю к нулю.

Производные этого семейства характеристик показаны на

рис. 9.2,6. Предположим, что kp - -- Тогда при %i-*0 производная упомянутых характеристик стремится к так называемой дельта-функции б (л:), равной нулю при любом л; О и обра-

вдающейся в бесконечность при л; = О, причем i)(x)dx=l *).

Для рассматриваемой характеристики релейного элемента (рис. 9.2,6) с высотой скачка 2ftp производная равна

Ф\{х) = 2кр6{х). (9.10)

Условно Фх (л;) можно изобразить, как показано на рис. 9.3, а, 2.

Аналогичным образом можно найти и производные иных, более сложных характеристик релейного элемента.

Так, для характеристики релейного элемента с положительным гистерезисом, как видно из рис. 9.3, 6, производная функции Ф2(х; о) равна

. ФИ;ст) = {

2kp6{x - Ко) при х> О, 2kp6 (х + Ко) при i < 0.

(9.11)

Ф2(х; а) изображена на рис. 9.3, 6, 2.

Для характеристики релейного элемента, не имеющего зоны нечувствительности, но обладаюпего отрицательным гистерезисом (рис. 9.3,6,7), производная Фз{х; а) получается заменой в (9.11) Ко на -Ко:

{2ftc6 (х -\- Ко) при X > С оЛ (9-12)

2kp6 {х - Ко) при л: < 0;

Фз(л:; а) изображена на рис. 9.3, в, 2.

Для характеристики релейного элемента с зоной нечувствительности (рис. 9.3, г, 1) производная функции Ф4(л:) равна

ФИx) = гp[б(x-Ko)-f б(х + Ко)] (9.13)

и изображена на рис. 9.3, г, 2.

*) Свойства дельта-функции 6{х) описаны в Приложении 3.

Для характеристики релейного элемента, обладающего положительным гистерезисом наряду с зоной нечувствительности (рис. 9.3, д,1), производная функции Ф5(л:; а) равна

kp [б {x - y,o) + 6{x + X%o)] при x>0 + Kq) + б (л; - Яко)] при i < О

(9.14)

и изображена на рис. 9.3, д, 2, где О < Я < 1 и ко > 0. Наконец, для характеристики с отрицательным гистерезисом и зоной

о

лг X

Ф1(х;в)

Ф5(х;б-)

.ХдХд X

Фs(x:(i)

О

Фе(х,е!)

<Ф'е{х;б1

Рис. 9.3. Характеристики релейных элементов н их производные.

нечувствительности производная Фб(л;; а) (рис. 9.3, е,/) может быть получена из (9.14) при Я> 1, хо>0, т. е.

ст) = {

йр[б(д;-Ко) + б(л: + Яко)] при i > О, kp [6{х + Хо) + 6 (л; - Яхо)] при л: < 0.

Производная Фб(л;; а) изображена на рис. 9.3, е, 2,

§ 9.3. Уравнение в вариациях при отсутствии зоны нечувствительности

Рассмотрим вначале характеристику релейного элемента не только без зоны нечувствительности, но и без гистерезиса, рис 9.3, а, 7. Для этого простейшего случая в соответствии с (9.10)

Ф' (х it); а) := Ф1 {X (t)) = 2ftp6 (х (t)). (9.16)

Здесь x{t) -периодическое решение частоты юо, причем такое, что

Но дельта-функция от периодического аргумента может быть представлена в виде *)

6(i(0)=ST

- \x-{tk)\

где th представляют собой корни уравнения

x{t) = 0.

(9.17)

(9.18)

т. е. моменты переключения. В силу периодичности x{t) эти моменты переключения для периодического режима равны (см. § 5.3)

(fe = 0, 1, 2, ...).

tk = k

Подставляя эти значения в (9.17) и учитывая, что в силу периодичности

получаем

б(х()) =

k = 0, 1, 2, ...

(9.19)

fe=0

Следовательно, согласно (9.10) Oi{x{t)) представится в виде

ФИг()) =

*) См. Приложение 3 (4-е свойство).

Так как для периодического режима согласно условию надлежащего направления переключения выполняется неравенство

i-(l<0,

то множитель

всегда представляет собой конечную

величину.

Из (9.20) следует, что 0\{x(t)) определяет собой последовательность импульсивных функций (дельта-функций) с периодом повторения, равным

Интенсивность или площадь каждой из этих импульсивных функций постоянна и равна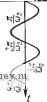

о л 1Е М: t

tJr, Ол Од Up

Наглядной иллюстрацией сказанному выше служит построение, приведенное на рис. 9.4, где изображено преобразование периодической функции x{t) в последовательность импульсов при помощи характеристики Ф( (х).

Подставляя найденные значения Oi{x{t)) в (9.9), запишем уравнение в вариациях для этого случая в виде

Рис. 9.4. Зависимость {х (<))

L{l(t)} = L{f,{t)}-Wip)L

Применяя теорему о линейности, согласно которой изображение суммы равно сумме изображений*), получим

Г (ё(0}=г(/ло}-

\щ У

ip)L{6(t-k)lit)}. (9.21)

Но для дельта-функции имеет место соотношение **)

L{&{t- УI (0) = J е-б а - и I (О dt = е- I {ta). (9.22)

*) См Приложение 1 (теорема I). **) См. Приложение 3 (3-е свойство).

Полагая в (9.22) ta = k - , уравнение (9.21) можно записать Б следующей форме:

2kr.

L{i{t)}L{um

W(p)Y,e -l[k). (9.23)

Применяя обычные обозначения для изображений

S(p) = L{g()), PAP)=-L[h{f)),

запишем уравнение (9.23) в виде

Wip)4p).

Здесь S*(p) определяется соотношением

(9.24)

(9.25)

(9.26)

ft=0

В уравнение (9.25), помимо изображения S(p) непрерывной функции КО, входит изображение Е*(р), соответствующее совокупности дискретных значений этой же непрерывной функции

при / = ft, т.е. Uk-)%

с. IP)

Wip)

Рис. 9.5. Линейная импульсная авгомагическая система соотвегсгвующая уравнению

п вариациях iH.25).

Можно считать, что уравнение (9.25) описывает некоторую линейную систему (рис. 9.5), состоящую из линейной части с передаточной функцией W(p), усилителя с коэффициентом уси-

и импульсного элемента (ИЭ).

*) Отметим здесь, что В*(р) представляет собой, по существу, определение дискретного преобразования Лапласа (см. книгу автора [12]), и для исследования уравнения в вариациях можно было бы воспользоваться аппаратом дискретного преобразования Лапласа. Мы, однако, в явном виде не будем привлекать этот аппарат,

Импульсный элемент преобразует непрерывную входную величину (t) (рис. 9.6,а) в последовательность импульсивных функций, интенсивность (или, что эквивалентно, площадь) которых изменяется пропорционально значениям входной величины Б дискретные равноотстоящие друг от друга моменты времени (рис. 9.6,6). Таким образом, импульсный элемент осуществляет модуляцию последовательности импульсивных функций

в соответствии с законом, определяемым входной модулирующей величиной. Это условно показано на рис. 9.7. Система, изображенная на рис. 9.5, является частным случаем импульсных

О

Рис. 9.6. К пояснению работы импульсного элемента.

Рис. 9.7. Импульсный элемент как модулятор.

автоматических систем (см. Введение). Структуру этой системы можно получить непосредственно из физических соображений, если учесть, что Ф\ {х {t)) определяет последовательность равноотстоящих друг от друга импульсивных функций с периодом

повторения

©о

Преобразуем уравнение (9.25) к такому виду.

чтобы из него можно было бы найти в явной форме изображения S*(p). Для этого применим соотношение, связывающее эти изображения:

2* (Р) = Т ё + S + 2/ о).

(9.27)

где S(р) в свою очередь определяется выражением (9.26).

Вывод этого соотношения приведен в Приложении 2. Для простоты дальнейших выкладок будем считать, что всегда выполняется условие

g(0) = limpS(p) = 0. (9.28)

Из соотношений (9.26) или (9.27) следует, что S*(p) является периодической функцией /и, т. е.

3(p + 2/scDo) = S(p),

(9.29)