Отсюда следует, что при А > Л™ =

Im [/i (соо) ~ Jy (ш„)] -

(8.51)

(8.52)

2 sin vyin

угол ф определяется из уравнения

Im [У, (шо) - 1у (ш)] - 2щ

cos (VYlK - ф) = -;г-р^-

И здесь имеет место картина, аналогичная описанной выше (см. рис. 8.17). Может оказаться, что на некоторой частоте (О = СОв одновременно выполняются условия существования субгармонических колебаний различного порядка. Возникновение тех или иных субгармонических колебаний зависит от предыстории состояния системы.

Выше везде шла речь о двух условиях существования вынужденных колебаний основной частоты или субгармонических различных порядков: об условии надлежащего момента переключения и условии надлежащего направления переключения. Что же касается третьего условия существования вынужденных колебаний основной частоты или субгармонических колебаний - отсутствия дополнительных переключений, то оно автоматически проверяется при построении формы вынужденных колебаний. Этому вопросу посвящена глава XI.

Если искомые вынужденные колебания (основные или субгармонические) существуют и они устойчивы, то это значит, что ранее существовавшие автоколебания иной частоты будут подавлены внешним воздействием или, иначе говоря, произойдет захватывание на частоте внешнего воздействия. В этом случае внешнее периодическое воздействие навязывает релейной системе свою частоту Шв или частоту coe/v и подавляет возможные б системе автоколебания. Такое свойство нелинейных систем часто эффективно используется для срыва автоколебаний и линеаризации релейных систем. Эти возможности будут подробно рассмотрены в главе XII.

Рис. 8.19. Определение параметров субгармонических колебаний ф и zq по кривым Г(-1 и Г,-.

§ 8.6. Примеры

Исследование вынужденных колебаний частоты шо или vcoo состоит в установлении условий их существования, исследования устойчивости, формы и максимальной величины вынужденных колебаний.

в настоящем параграфе рассматриваются лишь условия существования, т. е. определяются критические значения амплитуды Л внешнего воздействия, выделяющие области вынужденных колебаний частоты Шв = vcoo-

Устойчивость вынужденных колебаний исследуется в главе X, а определение их формы производится в главе XI.

1. Следящая система. Предположим, что к задающей оси следящей системы, автоколебания в которой рассматривались в предыдущей главе, приложено внешнее гармоническое воздействие частоты Шв = Шо.

ijlmJ(u)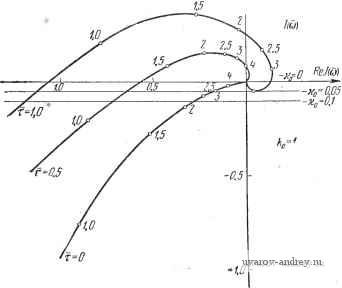

Рис. 8.20. Годограф / (со) релейной следящей системы прн и различных т.

Заметим, что если это воздействие является дополнительным, то оно может быть введено в систему различным образом. Примеры введения его описаны в § 1.1 и, в частности, для следящей системы один из таких способов приведен на рис. 1.24. Функциональная схема следящей системы имеет по-прежнему вид, изображенный на рис. 2.11, где следует считать, что

?о(0 = ?д(0=/15тК;-ф).

Для определения возможности существования вынужденных колебаний воспользуемся выражениями годографа релейной части системы /(со).

Годографы /(ш) при т=0; 0,5; 1, и k-X воспроизведены на рис. 8.20.

Используя выражение годографа /(со) (6.ЮГ) при 1=1,

находим по формулам (8.20) и (8.22) значения

А

при йо в виде

Ai кр ~~кГ

1 п

2 кр

(8.53)

и

IzKP

1 я . ,

1 +е

л о

СОо

1+е ® /J

(8.54)

11 кр

где йоиТм-

Зависимости -или - от ш можно непосредственно определить по графику /(ш) при kQ=l, если провести на этом же графике прямую -Построенные таким обра-

А

зом зависимости

, для хо==0 И т = 0; 0,5; 1, изо-

о 10

бражены на рис. 8.21, а -в соответственно. Области /, лежащие ниже кривой -Л^, соответствуют режиму биений или субгармоническому режиму. Области и /, лежащие между

кривыми -7- и

и выше кривой

соответствуют

ко ко -.f .. режиму вынужденных колебаний. В области / имеется одно периодическое решение 1ф1<, а в области - два периодических решения (ф1<--), [ф2 1>--)-

Влияние временного запаздывания сказывается на том, что частота автоколебаний, соответствующая Л] кр = О, смещается

1 кр

б сторону низких частот. Критические значения --- для т > О

Al кр

при малых значениях частот меньше ---, соответствующих

т==0, а затем при превышении некоторой величины ш становятся больше этих значений.

Предположим теперь, что Хо > 0. Тогда зависимости

А

-г- ОТ СОо изменятся. Эти зависимости для - = 0,05 и

==0,1 при различных т изображены на рис. 8.22 и 8.23, о - в соответственно.

0.В

0.2 О

ХоО

ID г.О 5.D f.D йв

i.D 2.0 ID W Cjb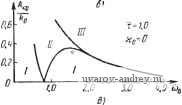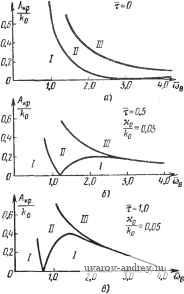

Рис. 8.21. Зависимости -~- or Og при Рис. 8.22. Зависимости от cog прн

=0,0,5. кр

W 1.0 to tp о ID То tp

0,6 O.-i 0.2

В

ш

Г'0,5 -0,1

о .о 2.0 3.0 4,0

Рис. 8,23, Зависимости от й3 при --=0,1.

Из этих зависимостей можно заключить, что влияние щ в некотором смысле качественно подобно влиянию временного запаздывания т.

Полученные графики позволяют выбрать частоту и амплитуду внешнего воздействия, при которых в системе будет возможен режим вынужденных колебаний частоты юо = ©в-. Рассмотрим возможность существования субгармонических колебаний. Обозначим частоту внешнего воздействия через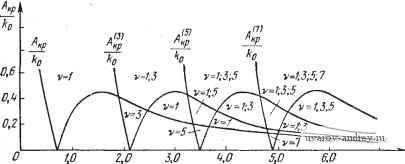

10 ыв

Рис. 8.24. Зависимости - от при Ио=0,5; -с=1, определяющие области существования субгармонических колебаний.

Шв = vшo; тогда субгармонические колебания будут иметь ча стоту ©0 = , где V = 3, 5, 7. Для существования субгармонических кодебаний необходимо выполнение условия (8.46)

1 кр>

где Л*1кр в рассматриваемом случае определяется из (8.53) при

Юв

замене щ на

, т. е.

1 кр

1 п\ т--+1

о

в частном- случае, при отсутствии запаздывания т = 0.

1 кр

I nv

7 fen

(8 55)

(8.56)

Зависимости от Шв при т = 1 изображены на рис. 8.24.

Здесь же приведена также зависимость -Эти зависимости

определяют области существования вынужденных колебаний основной частоты Шв = шо и субгармонических колебаний

СОо = порядка v. В каждой из областей указаны порядки

возможных колебаний. При малых амплитудах внешнего воздействия мы попадаем в области, где возможно существование только одного режима. С увеличением амплитуды возможно попадание в области существования нескольких режимов.

2. Система автоматического регулирования температуры. Предположим, что к релейному элементу системы автоматического регулирования температуры, функциональная схема которой имеет вид (рис. 2.10), приложено гармоническое воздействие

f(t) = Asin{aJ - ((>).

Определим область существования режима биений и вынужденных колебаний, т. е. зависимость /4,ф от со.

Для этого воспользуемся ранее построенным годографом /, (со) для /гп=1 при р = 0 (см. рис. 6.42).

Проведя на ней прямые -для значений х = 0, - = 0,015 (рис. 8.5), находим зависимости --г- и -г-, которые и при-

ведены на рис. 8.26 для Хо = 0 и на рис. 8.27 для - = 0,013.

Как и ранее, область / соответствует режиму биений (отсутствию периодических решений), область соответствует наличию двух периодических решений, отличающихся фазами, и область / - наличию одного периодического решения. В заштрихованной области возможно существование субгармонического режима порядка v = 3.

3. Электрический привод. Рассмотрим несколько иной пример, связанный с влиянием сухого трения на валу электрического привода при гармонически изменяющемся движущем моменте. Уравнения электрического привода были составлены в § 2.5, а в § 3.2 были построены переходные процессы при гармонически изменяющемся движущем моменте.

Предположим, что движущий момент электрического привода, описанного в § 2.5, имеет вид

f, (О = £ sin (соо^ - ф'),

и на валу его действует момент сухого трения. Тогда, как было показано в § 2.5, привод можно привести к некоторой эквивалентной релейной системе (см. рис. 2.16,6).

Передаточная функция линейной части системы равна

-0.15

Рис. 8.25. Определение -~ по годографу /(о системы регулирования температуры.

7 8

-0,05

}io О

К

jImJiu) ReM)

0,01 -0,04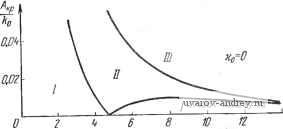

Рис. 8.26. Зависимости от tOg при >{о=0.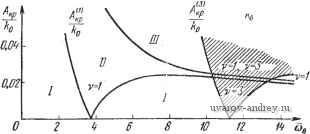

Рис. 8.27. Зависимости от при -=0,015, определяющие области существова-

иия субгармонических колебаний (v =3).

а приведенное ко входу релейного элемента внешнее воздействие в установившемся режиме будет равно *)

fit) =

sin (шо/ - ф' - arctg 7 а)) = А sin ((Oq - ф).

Функция f (t) представляет собой реакцию линейной части системы на гармоническое воздействие и физически соответствует 1тМ) скорости привода при отсутствии

сухого трения. Передаточная функция W{p) совпадает с точностью до обозначений с передаточной функцией, приведенной в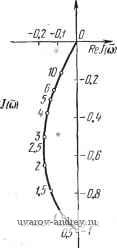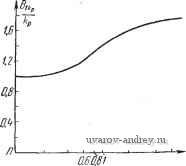

О/ OA

г 4 бШо'Т^ш

Рис. 8.28. Годограф /(о электропривода p c. 8.29. Зависимость от о) .

при учете сухого трения. ft в

графе 2 таблицы 6.4 (стр. 258). Поэтому можно записать годограф /(со) в виде

где /го = /гдв^р.

Вводя относительную частоту й = ш7 м, получаем

/(o) = -/ao{-i-(l-th-2f)+/th}.

(8.57)

Годограф /(со) при fto = 1 изображен на рис. 8.28. Критическое значение амплитуды согласно (8.20) будет равно

*) См. также § 3.5.

Так как амплитуда внешнего воздействия, приведенного ко входу релейного элемента, равна

то условие существования вынужденных колебаний

Л > Л, кр в развернутой форме примет вид

В

В. к

(8.59)

(8.60)

(8.61)

Зависимость критической амплитуды, отнесенной к ftp трения,

В> кр

т. е. -7-, от юо==соо/м, построенная по этому выражению.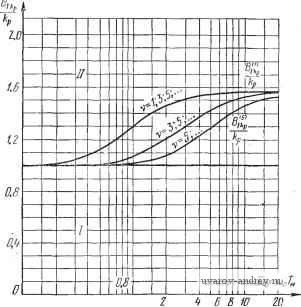

е,/ ОЛ DA 0.6 1.0

Рис. 8.30. Зависимости

b(v) кр

- от CDg, определяющие области существования субгармо-ннческих колебаний.

приведена на рис. 8.29. Область , лежащая выше этой кривой, соответствует режиму вынужденных колебаний. Условие существования субгармонических колебаний согласно (8.61) будет

иметь вид

где Mlp получается из (8.61) заменой ©о на

=/(¥--

Зависимости -г^- от Шв при v = 1, 3, 5 приведены на рис. 8.30.

Здесь же указаны области существования режима вынужденных колебаний и субгармонических режимов различного порядка v. Эти области расположены над соответствующими кривыми

Bnjkp.

Порядок субгармонических колебаний в соответствующих областях указан значениями v в областях, заключенных между кривыми Bilplkp и SlVp/ftp, где v = 3, 5, ... В области, лежащей ниже горизонтальной прямой Bi кр/kp = 1, вынужденные режимы отсутствуют. Здесь возможны режимы движения электрического привода с остановками (прерывистое движение).

Так как в режиме синхронизации или вынужденных колебаний на основной частоте или на субгармониках происходит подавление автоколебаний, то, выбирая надлежащим образом частоту внешнего воздействия, мы тем самым увеличиваем частоту периодического режима в релейной системе.

В ряде случаев такой способ повышения частоты периодического режима может оказаться более удобным, чем способы, описанные в § 6.4.