чения ее с прямой -хо в левой полуплоскости. Эти значения ф будут функциями у (рис. 8.7,а). Так, например, если имеются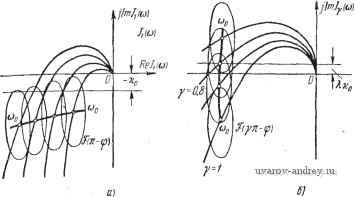

ReJviu)

уЧ у'0.8

Рис. 8.7. Семейство годографов Jj (со) и Jy (ffl) и прямые -И() kq К определению зависимостей Y=rj2 (со) и Y=rjY (со),

ф2v = Г2(Y), (8.290

два значения ф, то подобным образом можно найти зависимости Фп = Г„(у), Ф21 = Г21(у), (8.29)

которые на плоскости ф, у изобразятся в виде кривых (рис. 8.8).

Подобным же образом определяем зависимости

Ф1 = Г,(У),

пользуясь семейством годографов /у((й) и прямой -Хио- Разница здесь будет состоять лишь в том, что при q перемещении кривой, соответствующей S(YJt -ф), одновременно нужно изменять ееоцифровку, т. е. заменять значения фо на фо-[ я(1 -у)-Изображая зависимости (8.29) и (8.290 на плоскости ф, у, находим искомые значения ф и у как точки пересечения соответствующих кривых (рис. 8.8). Если кривые не пересекаются, то в системе может иметь место режим биений или субгармонический режим.

Для гармонического воздействия f (/) = Л sin(<uo< - ф) определение кривых Ф = Г(у) упрощается.

В этом случае

Рис. й-8- Определение параметров вынужденных колебаний Ф и v по кривым Tji и Г,у.

(уя - ф) = Aei

(8.30)

что соответствует окружности радиуса А. Поэтому вместо сложных кривых теперь из центров, лежащих на линии равных значений too, проводятся окружности радиуса А (рис. 8.9). Искомые фазы в этом случае можно определить непосредственно по чертежу, проведя радиус окружности из центра к точке пересечения ее с прямой -щ для /i (о) или прямой Я,ио для /(а)) в левой части плоскости. Углы, образованные этими радиусами и прямой -Ко или прямой Кщ, будут равны соответственно ф (рис. 8.9, а) иф--я(1-y) (рис. 8.9, б).

jfmJilu)

j=1 y0,8 a)

Рис. 8.9. Семейство годографов l\ (a) и !y (ш). К определению зависимостей у=Гп (со), и \==1у (со) при гар.-иоии1еском воздействии.

По этим данным находим искомые зависимости ф от y (8.30), по которым определяются значения ф и y- Число значений ф и соответствующих им y в этом случае не может быть больше двух.

Следует заметить, что если требуется установить условия существования вынужденных колебаний при заданных (одной или нескольких) частотах, то нет нужды строить годографы /i(a)) и /у((о) полностью, т. е. при всех значениях ю. В этом случае удобнее, задавшись необходимыми значениями со, изменять у от О до 1 и построить кривые равных значений соо, указанные на рис. 8.7 и 8.9 жирными линиями. Полученные кривые можно использовать для определения ф и у описанным выше образом.

§ 8.3. Релейные системы с несимметрией

Для релейной автоматической системы с несимметричной характеристикой релейного элемента и устойчивой линейной частью, изложенная в § 8.2 методика изменяется незначительно. Вместо (8.28) и (8.28) в рассматриваемом случае, как следует

(8.31)

(8.31)

из условий (7.14) и (7.14), получаем

Im (2я - Ф) + /, (СОо)} == - fn + Ко + г/о Wo (0), Re{(2rt - ф) + /,(соо)}> О

Im (у,2я - ф) + (СОо)} = - /п - Ко + г/о^о (0), Re {5(у,2я-ф) + /1 (соо)}<0,

где комплекснозначная функция (у12я -ф) при yi = 1 и Yi < <: 1 определяется выражением (8.25), а годографы релейной автоматической системы /i(a)), /у(со) -выражениями (6.60), (6.61). Теперь на плоскостях /i и Jy, где изображены семейства годографов релейных автоматических систем, проводятся прямые -/n-f-Ko + oWo(0) и /п -ко + г/о1У'о(0) (рис. 8.10), и на

JlmJtlu)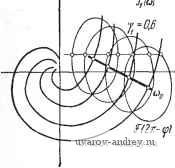

ReJ,i<j)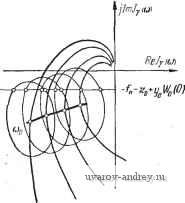

IfvZr-if)

Рис. 8.10. Семейство годографов /[ (со) и Jy (а). К определению .зависимостей у=Г|,-) (со)

плоскости /i(/v) принимаются во внимание лишь точки пересечения кривых (2я -ф) ((у12я -ф)) с прямыми, находящимися в правой (левой) полуплоскости.

Следуя изложенному в § 8.2, определяем зависимости ф от у

Ф11 = Г11(У1), Ф21 Г21 (Vl) Ф1 = Г1(У1). Ф2 = Г',(у,)

(8.32) (8.32)

и находим значения ф и ул как ординаты и абсциссы точек пересечения соответствующих кривых (рис. 8.11).

Для релейной автоматической системы с несимметричной характеристикой и нейтральной линейной частью из (7.16) и (7.16)

получаем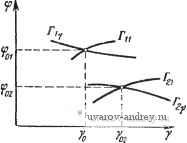

1т{5(2я-ф) + /,(соо)) = = - f п + 2о + щ,

Ке{5(2л-ф) + /(соо)}>0

(8.33)

Рис. 8.11. Определение параметров вынужденных колебаний ф н vo по кривым и Tiy.

\т{ (у,2я-ф) + /1 (соо)} =

= - fn + 2о - Я<),

Яе{5(у,2я-ф) + /,(с0о))<0.

(8.33)

В этом случае yi известно, а неизвестными величинами являются Zo и ф. Для определения Zo и ф на плоскости /i и Jy строятся при фиксированном значении yi годографы релейной автоматической системы /i(a)) и /(а)). В точках, соответствующих

jlmj,((j} /((j)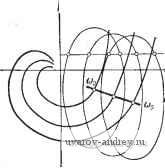

ReJ,(ui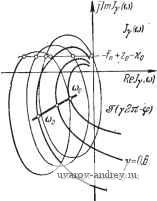

Рис. 8.12.

Семейство годографов /2 (со) и !у (со). К определению зависимостей 20 = Г,! (Ф)и го = Гг(Ф).

частоте юо, выстраиваются кривые, описываемые концом векторов 5(2я - ф) и 5(у12я - ф). Далее проводятся прямые -fn + ,+ Zo + xo, -fn + Zo -Ко (рис. 8.12). Точки пересечения кривой 5(2я - ф) с прямой -fn + 2o + Ko в правой полуплоскости и кривой &{у^п - ф) с прямой -fn -j- Zo - Ко в левой полуплоско-

сти определяют значения фо. Эти значения фо зависят от 2о. Изменяя Zo, т. е. положение прямых, находим зависимости ф от Zq. Так, если имеются два значения ф, то pi получаем (рис. 8.13)

Фп == Тц (Zq),

Ф1 = riY(Zo),

Ф21 = Г2, (Zo), (8.34) Ф2 = (2о).

У

ог hi в

Рис. 8.1-3. Определение г, и v по кривым Pjl н Г,-.у.

В точках пересечения этих кривых определяем искомые значения ф и Zo (см. рис. 8.13).

Если точки пересечения отсутствуют, то это значит, что в релейной автоматической системе вынужденные колебания частоты Юо отсутствуют, и возможен режим биений либо субгармонический режим. Для внешнего гармонического воздействия график функции

(Yi2k - ф) = Ле ( у^гя-ч (g 35)

представляет окружность и ф определяется углами, образованными радиусами окружностей и прямой -/п \-Zo-\-y или -U + Zo - Хо-

§ 8.4. Связные релейные системы

Исследование вынужденных колебаний в связных релейных автоматических системах сводится к определению сдвига фаз между внешним периодическим воздействием и вынужденным колебанием Zi (f) и сдвигов фаз од (ft == 2, 3, ..., А/, aj = 0) между вынужденными колебаниями hi(t) и Zh\(i) из условий существования вынужденных колебаний (7.19), (7.19). В общем случае при Л/ > 2 решение этой задачи весьма громоздко. Рассмотрим случай N = 2. Вводя комплекснозначную функцию

1 - Ф;) = 1 [foi - %) + Я~о1 (я - Ф,)] (8.36) k=\, 2

и пользуясь выражениями годографов связной релейной автоматической системы (6.90)

Ik (ю) = Re Jk (ю) -f / Irn Jk (©) =

2,fe(~H-a,)-bz2fe(-fcc )], (8.37)

ft = l, 2; a, = 0,

образуем сумму (я-}--}-/i (со). Условия существования вынужденных колебаний (7.19), (7.19) представятся в виде

1т {Sr 1(я -ф,) + /,(сй(,)} = -х„1, Re {ЗГ,(я-ф,) + /,Ы}<0

Re /2(00X0.

(8.38)

(8.38)

Условия (8.38) и (8.38) можно интерпретировать геометрически следующим образом.

Рассмотрим годографы связной релейной системы /i(cu) и /2(03), которые использовались для исследования автоколебаний (рис. 8.14). Проведем на плоскости /2 прямую -хог и определим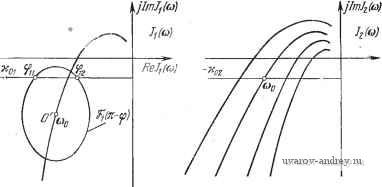

Рис. 8.14. Семейство годографов (ш) и /2 (<о). К определению зависимостей а=г,-2 (ф) и a=Tij (ф) при внешнем гармоническом воздействии. К определению параметров вынужденных колебаний а и ф.

ту кривую из семейства, которая пересекается с прямой -хо2 при со = (Оо. Параметр аг этой кривой определяет сдвиг фаз агз = а' (рис. 8.14,6). Далее на годографе /i((o) выбирается точка (О = (Оо и из этой точки строится, как из центра, кривая, описываемая концом вектора 1(я -ф1). Значения ф1 определяются как (см. рис. 8.14, а) отметки на кривой i(n -ф]) в точках пересечения ее с прямой -xoi, лежащей в левой полуплоскости.

Для гармонического воздействия

,5,(я--ф,) = ЛеИ -*

(8.39)

определяет окружность радиуса А. В этом случае из точки ш = (По годографа i\ (ш) проводится, как из центра, окружность (рис. 8.15,а). Проводя радиусы к точкам пересечения окружности с прямой -хоь расположенным в левой полуплоскости, определяем углы и ф12. Критические амплитуды Л,ф определяются обычным образом, как длина перпендикуляра, опущенного из

jlmff(o)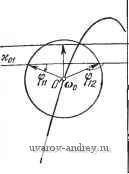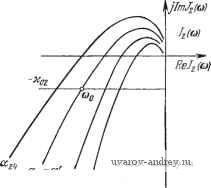

Рис. 8.15. Семейство годографов /, (со) и /j, (со). К определению параметров выиу;кдеиных колебаний а и ф при гармоническом воздействии.

точки О', соответствующей шо на прямую -xoi, если соо находится в левой полуплоскости 1\, либо как длина отрезка, проведенного из точки О' в точку пересечения прямой -xoi с мнимой осью, если Шо находится в правой полуплоскости i\. Отсюда следует, что если

Л<Ликр, (8.40)

то вынужденные колебания частоты шо отсутствуют. При

<А<А

12 кр

(8.41)

возможны два вынужденных колебания с частотой шо и различными фазами фи и ф12, причем

Ф„-Ьф,2=±я. (8.42)

При

А > Л,2, если Re /, (щ) < О, (8.43)

либо при

А > А22. если Re /, (соо) > О, (8.43)

существует только одно вынужденное колебание. Можно, как это было Сделано в § 8.1, определить i2kp и 51пф1 аналитически.

§ 8.5. Субгармонические колебания

Для исследования субгармонических колебаний введем комплексиозначную функцию

(V3t - ф) = Л [vfo {vn - ф) + По (vJt - ф)]. (8.44)

Эта комплекснозначная функция отличается от (8.1) тем, что масштаб Re(vn - ф) увеличен в v раз (v - целое число).

Для релейной автоматической системы с симметричной релейной характеристикой из условий (7.24) и (7.24) получаем

Im (vn - ф) + / (соо)} = - Ко, 1

Re{SГ(vя-ф) + (%)}<0, 1 -

где / (со) -годограф релейной системы (8.2). При v = 1 условия (8.45) совпадают с условиями (8.5). Строя кривые (\л - ф), где V > 1 - фиксированное нечетное число (v = 3, 5, 7), относительно начала координат, расположенного в точке со = шо, и

проводя прямую -Хо, определяем по оцифровке кривой -ф) значения фазы. При гармоническом внешнем воздействии

f (О = Л sin {aj + ф) ==

= Л sin (vcoo-f ф)

функция

9 {vK - ф) = Л [v cos(vn - ф)---f / sin (yn - ф)]

определяет собой эллипсы (рис. 8.16).

Значения ф1 и фг определяем по оцифровке комплексно-значной кривой ЗГ (уп - ф) в точках пересечения с прямой -хо-Если этих пересечений нет, то субгармонические колебания с частотой coq =-~ отсутствуют. Для существования субгармонических колебаний должно быть выполнено условие

А > Л,ко =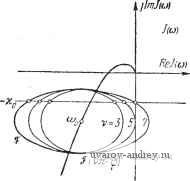

Рис. 8.16. Годограф / (со) и кривая F (vn-ф). к определению условий существования субгармонических колебаний.

Im/(-)+Xo=Im/(oo) + >c . (8.46)

Условия существования субгармонических колебаний (8.46) можно интерпретировать графически следующим образом. По

годографу / (соо) = / -j, на плоскости которого проведена пря-

jygj, xo, определяем при v = 1 зависимость Лкр = Лкр (рис. 8.17). При этом Шв = Шо. Для v = 3, 5, ... аналогичные зависимости Л'к^ получаются смещением Лкр вдоль оси частот на величины (v- 1)ш, где v = 3, 5, 7, ... Сплошной линией выделена огибающая критических амплитуд, ниже которой невозможно существование вынужденных колебаний основной частоты и субгармоник. Эта область соответствует биениям и сложным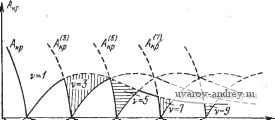

1 Do 2 Scjo Z 5щ г 7с)о Z Рис. 8.17. Области существования субгармонических режимов.

режимам. Заштрихованные области, находящиеся выше огибающей, соответствуют областям существования субгармонического режима порядка v = 3, 5, 7, ... С ростом порядка эти области уменьшаются (при хо = О они стремятся к нулю). В областях, лежащих выше заштрихованных, возможно существование нескольких субгармонических режимов. Тот или иной субгармонический режим возникает в зависимости от того, попадаем ли мы в Эту область при увеличении или при уменьшении амплитуды внешнего воздействия *).

В релейной системе с несимметричной характеристикой релейного элемента возможны субгармонические колебания как нечетного, так и четного порядка. Из условий (7.29) и (7.29) получаем

Im (v2n - ф) -Ь У, (соо)} = - f -f 2о -I- Хо,

где

(8.47)

Не{5Г(,2я-ф)-ЬУ(шо)}<0, -

Sr {уу,2к - ф) = Л [vf о (vY,2jt - ф) -f /То iyyfin - ф)] (8.48)

Re {v2n - Ф) -f /, (Шо)} > О J

Im (vY,2n -q>) + Jy (щ)} = - fn + Zq - Хц.

*) Подробное исследование субгармонических режимов принадлежит Сакаве [1], Жилю и П а ке [1], Ж и л ю, В е н г ж и н у и Паке [1]. См. также книгу Паке и Леметра [1].

и Vi = 1 или Yi < 0. а годографы релейной автоматической системы определяются по-прежнему выражениями (6.9) или (6.10). Далее повторяется построение, описанное в § 8.3, с заменой (Yi2n--ф) на (vYi2n -ф).

При гармоническом внешнем воздействии

f(0 = Лsiп(vo)o; -Ф)

9 (vYi2n - ф) = Л [v cos (vY2n - ф) + / sin (vYi2n - ф)]. (8.49)

При Yi = 1 и Yi < 1 функция (vYi2n -ф) определяет эллипсы. В точках (о = (Оо годографов релейной системы (со) и /(со) при фиксированных Yi строятся эллипсы 3 (v2n - ф) и (vYi2n -ф). Далее проводятся прямые -/ -}-Zo-f-Хд и -/п + 2о - Хо (рис. 8.18). Точки пересечения эллипса (v2n -ф)

jImJy (О)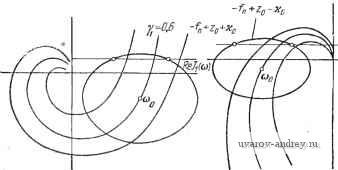

Рис. 8.18. Семейство годографов J] (со) и 1у (со). Определение зависимостей zo=r,-i (ф^) и 2д=Г(у (Ф) для субгармонических колебаний при внешнем гармоническом воздействии.

С прямой -fn + Zo + o в правой полуплоскости и эллипса (Yiv2n -ф) с прямой -fn + 2o-~X(5 в левой полуплоскости определяют значения ф. Эти значения зависят от Zq. Изменяя Zo, находим зависимости

и, аналогично.

Ф11 = Гн(го), Ф21 = Г21(го)

Ф1 = Tlv (о). Ф27 = Г\ (Zo).

(8.50) (8.500

Точка пересечения этих кривых (рис. 8.19) дает значения фо и Zo. Это построение для любого v определяет возможность существования субгармоник v-ro порядка. Исключая -fn + 2о из равенств (8.47) и (8.470, получаем при учете (8.49)

Л [sin (v2n - ф) -- sin (Yiv2n - ф)] == 2xq - Im [У, (coq) - ( >o)l-